5083铝合金GTN损伤参数求解与成形极限预测

刘纯国 ，王廖子 ，姚作杨

(1. 吉林大学 辊锻工艺研究所，吉林 长春，130022；2. 吉林大学 材料科学与工程学院，吉林 长春，130022)

“十三五”以来，国家“八横八纵”高铁网络全面推进，高铁在国家经济建设以及重大战略安全的地位越来越高[1-2]。铝合金密度小，比强度、比刚度高，成本适中[3]，是高速动车组车体的主要材料。随着新一代智能高铁与磁悬浮等高速车辆运行速度的提高，大尺寸、多曲率、长棱线流线型车头5083 铝合金蒙皮零件越来越多。然而受制于铝合金成形性能，带棱线蒙皮零件成形中易发生断裂，产品外观和精度难以保证，无法满足新一代高铁的要求。如何充分利用其塑性成形性能，预测板料的成形极限，优化成形工艺，获得高质量蒙皮零件，引起越来越多研究人员的重视。

目前，有关5083 铝合金成形极限研究主要以经典塑性力学和宏观损伤力学模型为主，缺乏材料内部的细观结构与宏观力学的联系。Gurson-Tvergaard-Needleman(GTN)模型是细观损伤模型中应用最为广泛的模型之一，它将材料内部微孔洞的形核和长大与材料宏观的应力、应变场相关联，对韧性金属的断裂预测有良好的效果[4-6]。UTHAISANGSUK等[7]使用GTN模型预测了H220BD+Z钢板的成形极限，并且预测结果与试验结果保持了很好的一致性。SAFDARIAN[8]利用GTN模型成功预测了6061铝合金的成形极限图(FLD)。TENG 等[9]采用GTN 模型预测了铝合金5A06 板材成形过程中的韧性断裂行为。KAMI等[10-11]在GTN 模型中考虑了板材的各向异性，能够更加真实地反映金属板材的损伤破坏机制。LI等[12]使用GTN 模型研究了AA7075-T6 铝合金在热成形过程中的损伤演化规律。NAHSHON 等[13-14]分别对GTN 损伤进行修正，以改进其在剪切载荷下预测韧性断裂结果较差的缺陷。NIELSEN 等[15]使用剪切修正后的Gurson 模型，对延性剪切下的界面破坏进行了数值分析，得到了良好的结果。YAN等[16]使用GTN损伤模型研究了S700材料冷成形下的延性破坏，并校准了GTN 模型屈服面中的修正参数q1、q2和q3。GAO 等[17]将GTN 损伤模型成功应用于预测AA7075-T6B柱在热成形过程中的成形性和损伤分布，证明了基于GTN 模型的数值模拟在工业化成形应用中具有较高的可靠性和准确性。

本文作者将GTN损伤模型应用于5083铝合金板料的成形极限预测。通过扫描电镜确定GTN 损伤参数的取值范围，利用响应曲面法和遗传算法，最终确认符合拉伸试验结果的最优损伤参数；将获得的GTN 损伤参数引入有限元模型，预测5083铝合金板料的FLD；设计并进行Nakazima 胀形试验，将数值模拟结果与实验结果进行对比分析。

1 GTN损伤模型

在前人研究的基础上，GURSON[18]将孔洞体积分数引入塑性屈服准则中，反映了材料塑性变形过程中细观损伤程度对屈服面的影响。通过建立孔洞演化规律和塑性势之间的联系，描述金属材料在塑性成形过程中孔洞演化对材料塑性变形的影响，从而将损伤演化和材料的本构方程紧密的耦合起来，如式(1)所示。

式中：σe为宏观层面的等效应力；σy为微观层面的等效应力；σm为静水应力；f为当前孔洞体积分数。

TVERGAARD 等[19-20]对Gurson 模型进行了改进和完善，考虑了孔洞之间的相互作用以及材料的应变强化效应，通过引入修正系数改变了孔洞体积分数的表达式，补充了对孔洞萌生和贯通过程的描述。修正后的GTN 模型能够较好地模拟拉伸载荷作用下材料自孔洞萌生至最终断裂的整个损伤演化过程。适用于各向同性强化材料的GTN屈服函数具有以下形式：

式中：q1，q2和q3为修正系数；f*为贯通发生后孔洞体积分数。

f*函数被用来考虑材料失效前孔洞迅速贯通的过程。当材料内部的孔洞体积分数f达到贯通准则所确定的临界值，即fc≤f＜ff时：

式中：fc为孔洞开始贯通时的临界孔洞体积分数；ff为材料最终失效时的孔洞体积分数。贯通开始前，孔洞体积分数的变化来源于现有孔洞的长大以及新孔洞的形核，可以表示为：

式中：为原有孔洞长大引起体积分数的变化率，当材料处于初始状态时，等于f0；为新形核孔洞引起的体积分数的变化率。

根据质量平衡原理，假设所研究的特征体积单位周围的孔洞是不可压缩的，并且孔洞的增长取决于材料的塑性变形，与塑性应变的静水分量有关：

式中：为塑性应变的静水分量。

新孔洞形核的主要形式是基体粒子在界面处的断裂或脱粘,应变控制的孔洞形核准则可表示为：

式中：为等效塑性应变率；A为孔洞形核系数，是基体等效塑性应变的函数，服从正态分布：

式中：fn为孔洞体积分数中形核部分的极限值；εN为孔洞萌生时的平均等效塑性应变；sN为该正态分布的标准差。

在GTN 损伤模型中孔洞体积分数的增加实现了损伤的累积，孔洞体积分数作为一个损伤标量来判定材料的损伤及断裂行为。当材料的孔洞体积分数达到其所能承受的临界值时，在外载荷的作用下材料内部的微孔洞会发生聚集并连接在一起，形成微缺陷进而发展为宏观裂纹，材料的承载能力发生急剧下降，最终导致部件的断裂。

2 5083 铝合金板料GTN 损伤参数求解

2.1 板料参数及性能

本文使用厚度为2 mm 的5083-H111 铝合金板料，材料成分见表1。按照国家标准制备拉伸试样，标距为50 mm。以1 mm/min 的拉伸速度进行单轴拉伸试验，并重复3 组试验以保证试验结果的可靠性。试验所得真应力σ-真应变ε曲线如图1 所示。经Ludwick硬化方程拟合得σ=153.3+582.7ε0.5954。

表1 5083-H111铝合金板料的化学成分(质量分数)Table 1 Chemical composition of 5083-H111 aluminum alloy%

图1 材料的真应力-真应变曲线Fig. 1 True stress-strain curve of material

2.2 实验法测定损伤参数范围

GTN 损伤模型中有9 个参数需要确定，即f0、fn、fc、ff、q1、q2、q3、sN和εN，其中，q1、q2、q3是材料性能相关系数，sN和εN通常被视为常数，可以通过经验确定。根据参考文献[21]，取q1=1.5，q2=1.0，q3=2.25，sN=0.1，εN=0.1。因此，本文主要确定以下4个损伤参数：初始孔洞体积分数f0、可形核孔洞体积分数fn、临界孔洞体积分数fc和断裂孔洞体积分数ff。

将需要拍摄的部位制成镶嵌件以便打磨制样，考虑到铝合金材质偏软，使用15、10、6.5、4、2.6 μm 的砂纸依次打磨；打磨完成后使用抛光机进行抛光，确保试样表面呈现镜面状，光洁无划痕；用凯勒试剂对试样腐蚀一段时间，最后，用酒精清洗试样并吹干。试样制备完成后，使用扫描电镜观测拉伸试样在不同变形阶段的微观孔洞变化，如图2所示。可见：板材在变形前存在少量微小孔洞，这与其轧制工艺有关。随着变形量逐渐加大，原有孔洞体积增加并有新孔洞形核，孔洞数目增多。试样拉断后，断口上有韧窝分布，是典型的韧性断口的特征(图2(d))。孔洞之间存在着垂直于加载方向(加载方向为图片平面法线方向)的二次微孔洞，这类次级孔洞在一次孔洞之间剪切带上较小粒子的附近萌生，使还没有充分生长的2 个一次孔洞在还存在一定间距时就发生了贯通。通常这种情况易出现在强度较高的受到较大剪切载荷的金属或合金中，通过二次微孔洞体积的增长实现各个孔洞之间的聚合贯通，最终完全分离断裂。

图2 不同变形阶段试样的SEM照片Fig. 2 SEM images of samples during different deformation phases

通过Image-Pro Plus(IPP)图像分析测量孔洞的面积比，进而确定孔洞体积分数。各个损伤参数的范围如表2所示。

表2 损伤参数的范围Table 2 Range of damage parameters

2.3 GTN损伤参数响应面模型建立

通过扫描电镜观察孔洞占比往往存在误差，需要大量的数据处理才能得到准确的损伤参数。本文采用响应面法(RSM)，基于中心复合设计(CCD)给出各因素与响应变量之间关系的多项式模型，最终通过遗传算法计算最佳参数。

以应力-应变曲线中特征点的4 个关键值，最高点应变R1、最高点应力R2、断裂点应变R3、断裂点应力R4作为响应值，如图3 所示，将GTN 模型参数f0、fn、fc、ff作为4 个影响因素，应用Design Expert软件，用四因素三水平的中心复合实验设计方法，设计28 组单向拉伸的仿真实验。通过Abaqus/Explicit 对单轴拉伸试验进行有限元仿真，有限元模型如图4 所示。选用C3D8R 八结点线性六面体单元，平行直线段内的网格尺寸为0.5 mm，平行直线段外的网格尺寸为2 mm。将试样一端的夹紧区域限制为完全固定，参考点(RP)设置在另一夹紧端边界的中心，并设置运动耦合关系以施加位移边界条件。将参考点处的支反力视为实际试验中的载荷，在直线段上选择间距为50 mm的对称的两点建集，它们之间的位移差可视为引伸计标距内的变形量，以此获取的载荷-位移曲线更加贴合实验情况。28 组仿真试验完成后，提取载荷-位移曲线并转化为工程应力-应变曲线以获取4个响应值。表3所示为28组影响因子组合及其响应值。

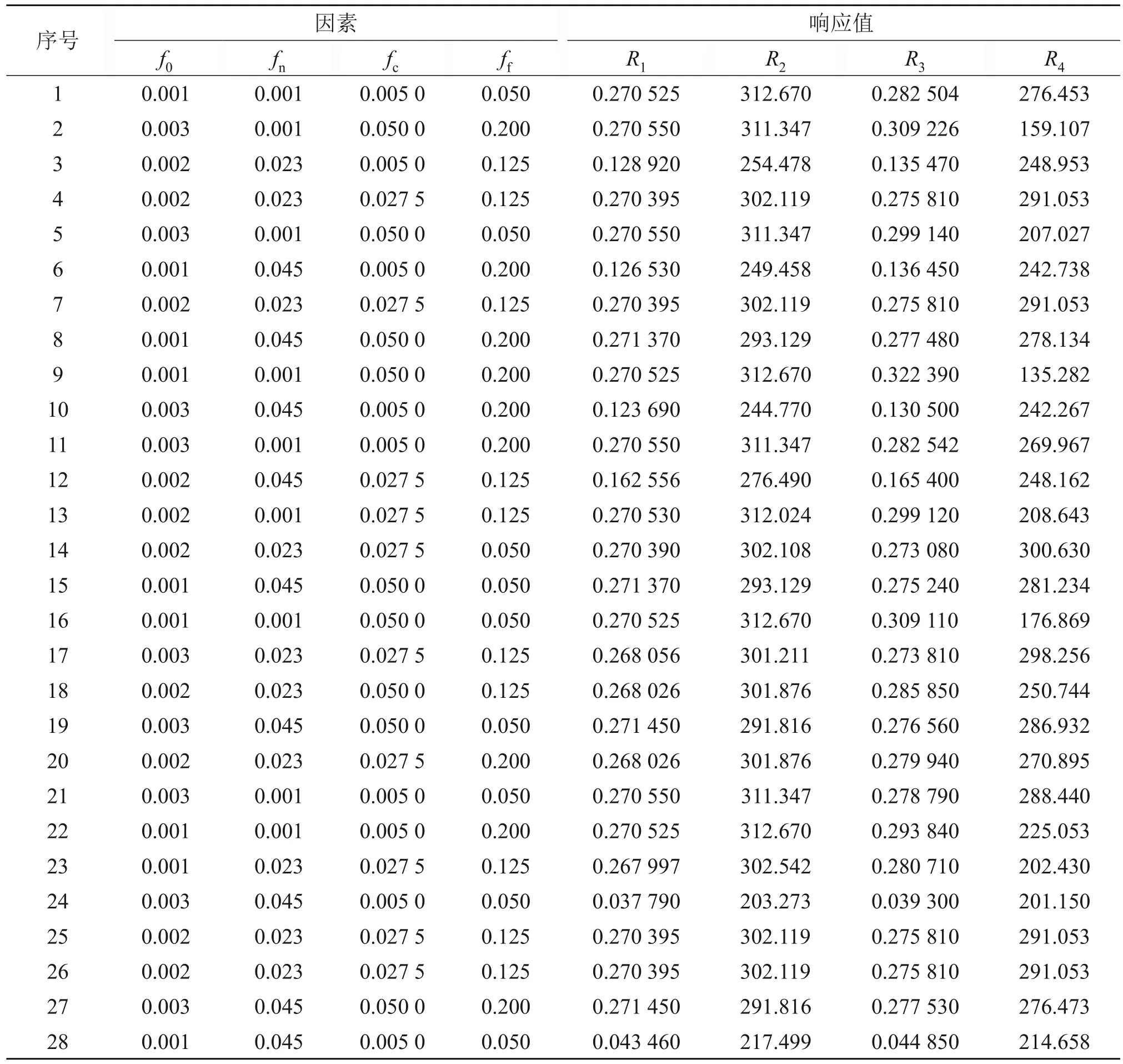
表3 中心复合实验设计方案及其响应值Table 3 Central composite experimental scheme and responses

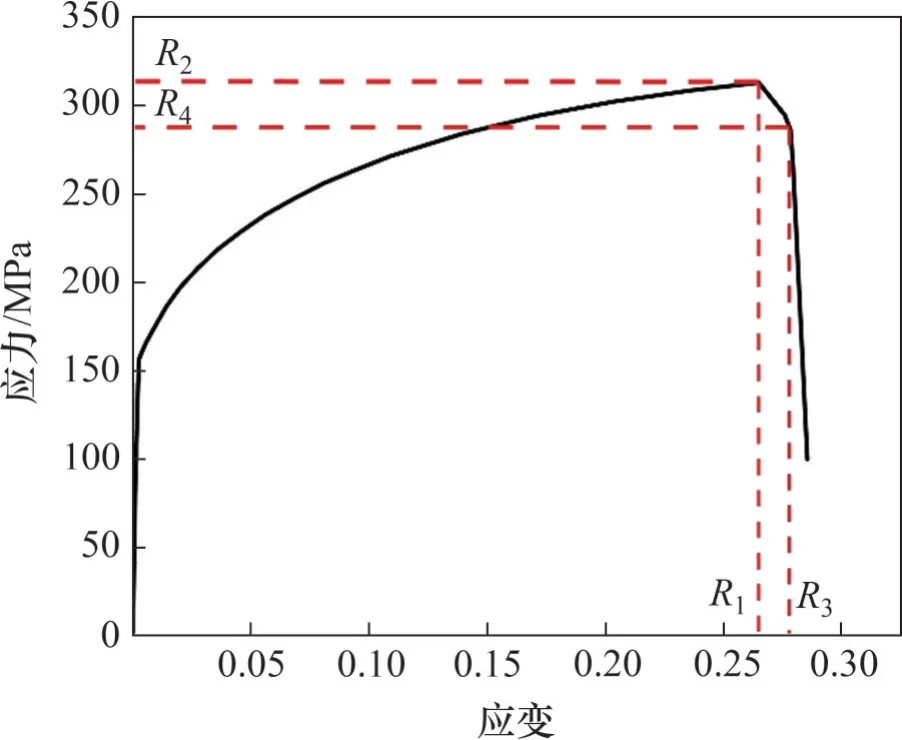
图3 响应值的选取Fig. 3 Selection of response value

图4 拉伸试验有限元模型Fig. 4 Finite element model of tensile test

响应面模型的分析结果表明，模型显著性检验p值小于0.000 1，说明本文建立的模型具有统计学意义；多元相关系数R2＞0.95，调整决定系数为0.942 6，二者均接近1，说明模型数据拟合良好；变异系数为7.58%，说明实验的可信度和精确度高。综合以上分析可得，建立的响应面模型能够准确地反映损伤参数对拉伸曲线的影响。

2.4 损伤参数对成形性能的影响

响应面模型经方差分析后，略去不显著项，所得编码方程(coded factors)如下：

通过比较编码方程每个因素的系数可以评估它们的相对影响，高水平为正值，低水平为负值。可见，4 个影响因素中，fn和fc对应力应变曲线的影响较大，而f0和ff的影响较小；f0仅对最高点应力有较为明显影响，f0增大，初始的孔洞体积占比变大，最高点应力小幅度降低；ff仅对断裂点的应力应变有所影响，ff增大使得断裂的发生需要经过更长时间的孔洞体积累积，一定程度上延缓了断裂的发生，故断裂点应变有所增大，而应力有所降低；fn是对拉伸曲线影响最大的因素，可形核孔洞体积分数对应于材料中的缺陷，其值越大，意味着材料强度、塑性的下降以及更早的颈缩和断裂；临界孔洞体积分数fc对应着材料经历局部塑性变形所需的聚集孔洞体积分数。因此，当fc较小时，孔洞聚集所需的变形相对较少，材料宏观则表现更早出现颈缩和失效。图5所示为4个参数两两之间对断裂点应变(R3)交互作用的响应面模型。由图5(d)可以看出：fn与fc之间存在较强的交互作用，当可形核孔洞体积分数fn增加而临界孔洞体积分数fc减少时，材料断裂点应变急剧下降。

图5 不同参数组合对材料断裂点应变(R3)交互作用的响应面模型Fig. 5 Response surface of interaction between different parameter combinations on strain value at fracture point of material failure(R3)

2.5 GTN损伤参数优化

得到多元二次回归方程后还需进行优化，使模拟结果更加贴合试验结果。与传统的优化方法相比，遗传算法以生物进化为原型，具有很好的收敛性，在确保计算精度的同时，计算时间少。因此，以f0、fn、fc、ff为优化变量，将单轴拉伸试验获得的工程应力-应变曲线上的最高点(R1、R2)和断裂点(R3、R4)作为优化目标，使用NSGA-II 遗传算法得到损伤参数的优化结果。经过优化计算，确定损伤参数f0、fn、fc、ff分别为0.001 837 7、0.017 543 3、0.031 307 5、0.059 339 2。将所得损伤参数引入单向拉伸有限元模型中，对单向拉伸过程进行数值模拟，并将数值模拟获取的应力-应变曲线与拉伸试验结果进行对比，如图6所示。从图6可见：两条曲线具有较高的匹配度，最高点相对误差小于5%，断裂点相对误差小于4%，说明最终确定的损伤参数是合理的。

图6 应力-应变曲线对比Fig. 6 Comparison of stress-strain curves

3 5083铝合金成形极限预测

采用ABAQUS/Explicit 对Nakazima 胀形的试验过程进行数值模拟，将最终确定的GTN 损伤参数引入有限元模型中，建立的胀形有限元模型如图7所示，主要包括圆顶凸模、压边圈、胀形试样和凹模4个部分。对薄板进行模拟计算时，通常将板料设置为壳单元简化计算，本文由于计算引入了孔洞体积分数，为满足计算的需要，故将试样定义为三维实体部件、可变形体；模具简化为壳部件、离散刚体；各组件之间的接触设置为面面接触类型，摩擦因数设置为0.15。对各部件进行网格划分，板料选用C3D8R八结点线性六面体单元，模具选用R3D4 四结点三维双线性刚性四边形单元。综合考虑计算的精度和效率，结合模型中板料的实际尺寸，将模具的网格尺寸定义为3 mm，板料的网格尺寸定义为2 mm。边界条件设置尽量与试验条件保持一致，凹模设置完全固定约束，给予压边圈100 kN 的压边力。凸模的运行采用位移控制方式，运动行程设置为40 mm，凸模位移速度控制在1 mm/s。试样宽度为20～180 mm，以试样宽度梯度20 mm共制备9个试样。成形后的孔洞体积分数分布云图如图8所示，达到断裂孔洞体积分数的单元被视为失效单元而自动删除，产生断裂的视觉效果。宽度较窄的试样(图8(a)和8(b))裂纹出现在正中心，较宽的试样受摩擦条件影响，裂纹出现在偏离中心位置的两侧。提取失效单元处最大的主应变和次应变，以此数据绘制有限元预测的FLD。

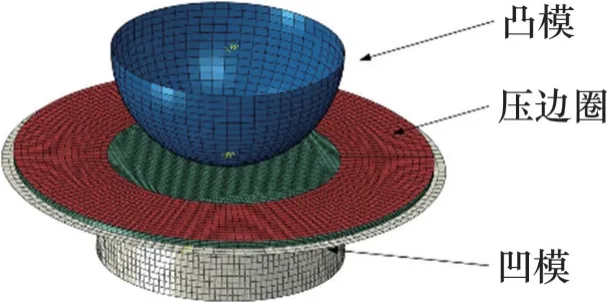
图7 Nakazima试验有限元模型Fig. 7 Finite element model of Nakazima test

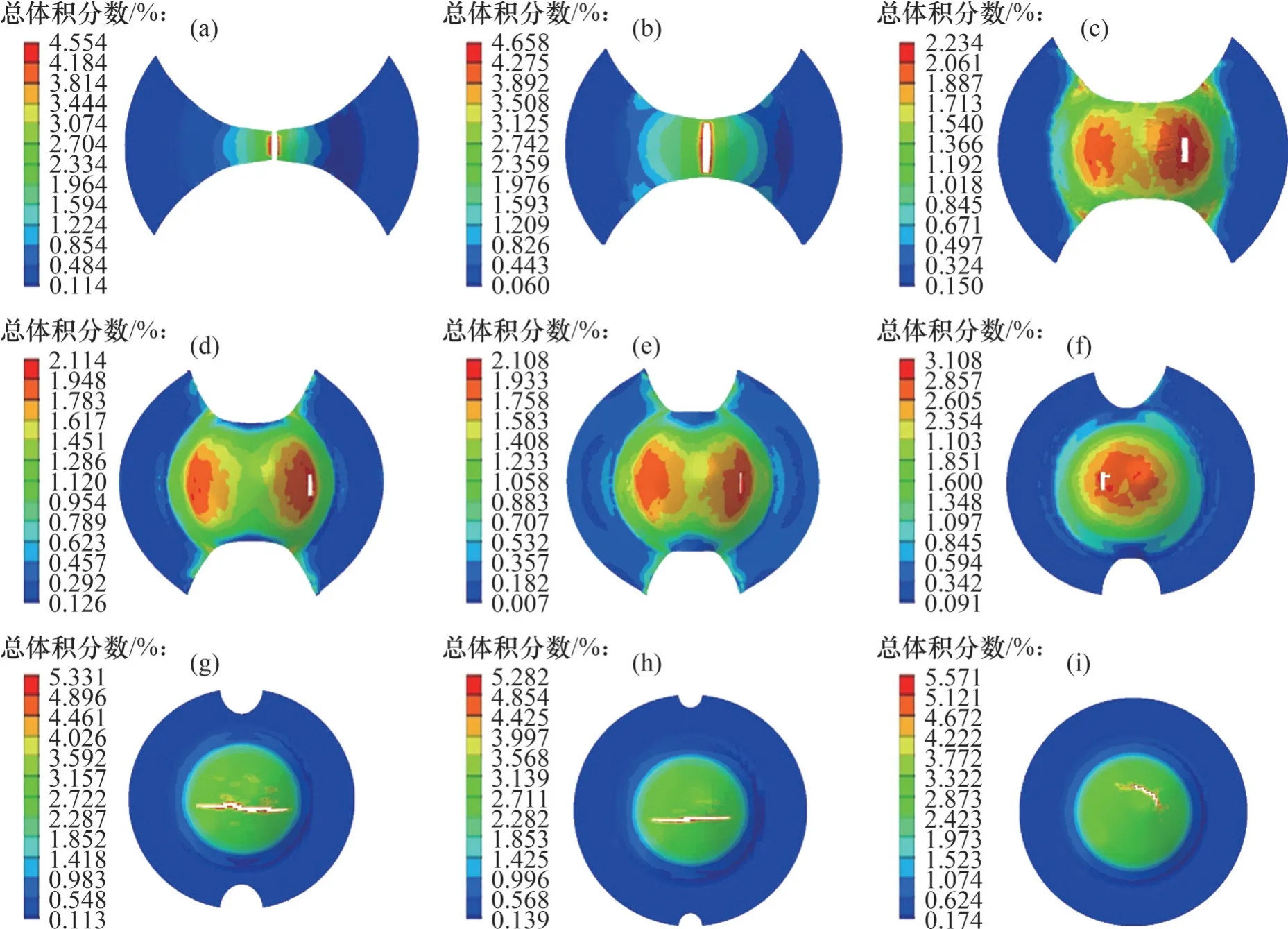
图8 试样成形后孔洞体积分数分布情况Fig. 8 Distribution of void volume fraction after samples forming

图9所示为孔洞体积分数随等效塑性应变变化的曲线。从图9可以看出：在成形过程的前期，孔洞体积分数的增长主要依赖新孔洞的形核，初始孔洞生长所带来的孔洞体积分数增加与之相比几乎可以忽略不计的。当达到孔洞可形核部分的极限值fn时，不再有新的孔洞生成。此时，孔洞体积分数的增长全部由现有孔洞的生长引起，直至增长达到断裂体积分数ff时引发材料的断裂。从总体来看，孔洞形核后首先会经历一个缓慢的成长过程，在临近断裂应变时，孔洞长大引发的体积增长迅速增长，随后发生破坏。对比不同应变状态下孔洞增长情况的差异，双拉变形区先于拉压变形区到达断裂体积分数。造成这种情况的原因主要是拉应力对孔洞生长具有促进作用，导致双拉变形区孔洞长大速度快于拉压变形区，而孔洞形核基本不受应变状态的影响，最终使双拉变形区的总孔洞体积增长速度大于拉压变形区的总孔洞体积增长速度，在宏观上表现为双拉变形区的成形极限低于拉压变形区的成形极限。

图9 孔洞体积分数与等效塑性应变的关系Fig. 9 Relationship between void volume fraction and equivalent plastic strain

4 Nakazima胀形试验

在EC系列板料成形实验机上进行Nakazima胀形试验，胀形前通过电化学腐蚀的方法用2 mm的圆网格对9个试样进行打标，以便后续测量样品成形后的主应变(ε1)和次应变(ε2)。试验结束后，使用ARGUS光学非接触式应变测量设备获取胀形试验件的应变信息。图10 所示为胀形试验成形后的试样。可见：9个试样的断裂位置都出现在试样中心区域，未出现拉延筋位置和边缘部位断裂的情况。

断裂后拉压变形区域和双拉应变形区域的试样与数值模拟结果进行对比，如图11所示，可见：断裂位置基本一致。将凸模的载荷-位移曲线数值模拟结果与试验结果进行了对比，结果如图12 所示。可见：载荷增长趋势一致，最大载荷及其对应的位移的相对误差小于3%。

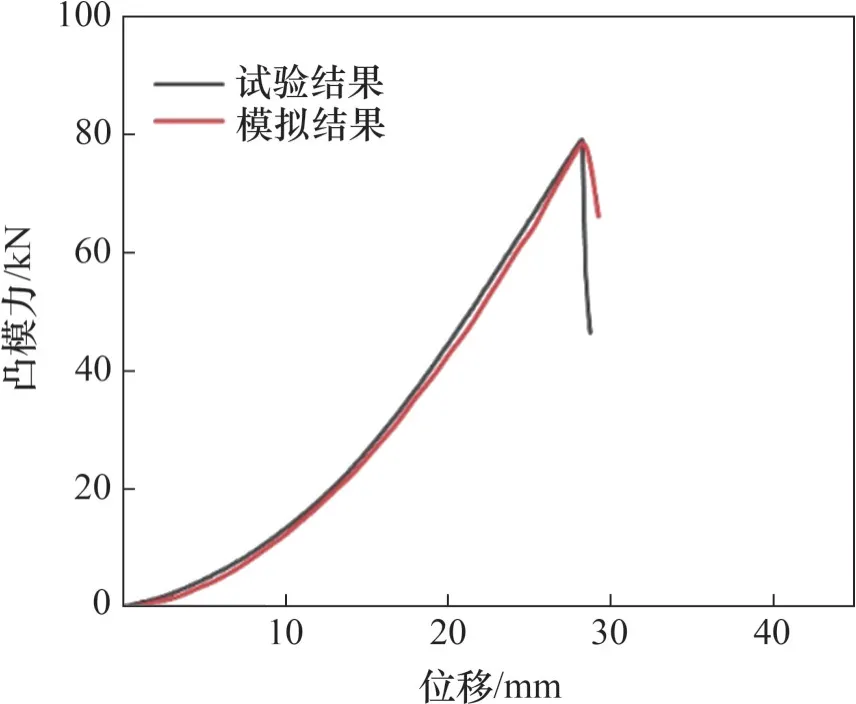
图12 载荷-位移曲线对比Fig. 12 Comparison of load-displacement curves

图13 所示为实验构建的FLD 与数值预测结果的对比。结果表明：以GTN 损失模型为失效准则预测出的FLD 与实验结果吻合程度较高，趋势基本一致，局部相对误差在10%以内。其中，右侧双拉变形区精度略低于左侧拉压变形区精度，主要原因是有限元接触设置不能完全还原试验中复杂的摩擦条件，导致极限应变出现差异。

图13 模拟与试验所得FLD对比Fig.13 Comparison of FLD between simulation and experimental results

5 结论

1) 以扫描电镜的观测结果为基础，通过中心复合实验设计方法设计单向拉伸仿真实验，建立二阶响应曲面模型，应用遗传算法进行参数优化，确定5083铝合金的GTN损伤参数。将确定的损伤参数赋予单向拉伸有限元模型，所得应力-应变曲线与试验所得曲线基本吻合，相对误差在5%以内，证明了该方法有效性。

2) 数值模拟获取的凸模载荷-位移曲线与试验结果匹配度较高，相对误差小于3%；对Nakazima胀形试样断裂位置的预测也具有较高的准确性；以GTN损伤模型作为失效准则预测的5083铝合金成形极限图与试验所得结果吻合程度好，相对误差在10%以内，表明本文方法能够被用于高铁5083 铝合金蒙皮零件成形中的断裂预测，进而提高零件成形质量。