钢轨波磨对高速车辆-道岔系统动力性能的影响

李智恒 ，闫正 ，李抒效 ，徐井芒 ，王平

(1. 西南交通大学 高速铁路线路工程教育部重点实验室，四川 成都，610031；2. 西南交通大学 土木工程学院，四川 成都，610031)

钢轨波磨是指新的钢轨在铺设使用后，随列车荷载的反复作用，逐渐在钢轨轨面出现波浪形周期性磨损的现象，是一种常见的钢轨缺陷形式[1-3]。随高速列车运行速度的提高、轴重的增大以及车流密度的加大，高速道岔出现钢轨波磨的现象越来越普遍[4]，图1 所示为京沪高铁某道岔区段钢轨波磨。当列车通过存在波磨的道岔时，轮轨动态相互作用会明显加剧，岔区振动也会加强，对道岔的轮载过渡产生不利影响，甚至对列车过岔的安全性构成潜在威胁。因此，探究钢轨波磨对高速道岔动力学性能的影响具有重要意义。

图1 高速道岔钢轨波磨Fig. 1 Rail corrugation of high speed turnout

国内外众多研究者在钢轨波磨机理和钢轨波磨对车轨耦合系统动力特性的影响规律等方面开展了大量研究。GRASSIE等[5-7]认为钢轨波磨的波长不能说明钢轨波磨的产生机理，可利用固定波长机理和钢轨初始损伤机理来说明。ZHAO等[8]采用有限元方法建立了高速铁路车辆与轨道相互作用的三维瞬态滚动接触有限元模型，考虑了车辆子系统和轨道子系统，保证了车辆-轨道相互作用在垂向和纵向上的精确求解。JIN 等[9]采用数值方法研究了钢轨波磨的发展及其对车辆轨道耦合动力学性能的影响，结果表明钢轨波磨对车辆和轨道零部件振动的影响较大。宋小林等[10-11]通过构建多体动力学仿真模型，以实测钢轨波磨为激励研究波磨对轮轨系统动力特性的影响，发现波深时变率与轮轨垂向力和钢轨垂向加速度间存在明显对应关系。张鹏飞等[12]通过现场测试，基于地铁线路普通道床地段钢轨波磨和钢轨振动加速度获取了地铁波磨的分布特征，并通过动力学模型仿真分析提出了以钢轨打磨来控制波磨的波深安全阈值。钟硕乔等[13]发现钢轨波磨主要影响车辆系统的垂向振动，即随波磨幅值增大，轮对和转向架的垂向加速度以及轮轨垂向力均呈增大趋势。李伟等[14]通过实测钢轨打磨前后车辆和轨道零部件的振动加速度，解释了一系钢弹簧和扣件疲劳断裂的主要原因，即钢轨波磨导致了车辆和轨道零部件的强烈振动。宋志坤等[15]研究了柔性轮轨下轮轨波磨综合作用的振动特性。刘志伟等[16]建立重载机车-轨道刚柔耦合动力学模型，得到钢轨波磨激励下轮对、构架和车体的振动响应。刘国云等[17]同样建立了车辆-轨道刚柔耦合动力学模型，分析了车速、波磨特征对车辆系统振动响应的影响规律。郭涛等[18]充分考虑了柔性轮对的共振模态，研究了钢轨波磨对车辆动力学性能的影响。从上述文献可以看出，绝大多数研究专注于区间线路钢轨波磨对车辆轨道系统动态响应的影响。而作为轨道三大薄弱环节之一的道岔，其轮轨动态相互作用远比区间线路的复杂，钢轨波磨对车辆过岔性能的影响规律也与区间线路的不同，因此有必要针对该问题开展深入研究。

本文通过对实际运营高速道岔区段的钢轨波磨进行大量调研，基于车辆-轨道耦合动力学以及子结构模态叠加法，建立高速车辆-道岔刚柔耦合动力学模型，以钢轨波磨作为轨道激扰源，研究钢轨波磨对道岔区轮载过渡的影响；同时分析不同波磨相位、波长、波深和运行速度下钢轨波磨对轮轨动态相互作用以及车辆部件振动特性的影响，为道岔区钢轨的打磨处理提供理论参考。

1 模型建立

1.1 车辆-道岔刚柔耦合动力学模型

1.1.1 车辆模型

为研究道岔区钢轨波磨对高速车辆过岔动态性能的影响，本文基于多体动力学理论，在动力学软件SIMPACK中建立高速车辆模型。该模型主要由车体、转向架、轮对和轴箱组成，其拓扑图如图2所示，该拓扑图考虑了轮对的弹性变形，其他部件均简化为刚体。图2 中，y表示线路横向方向自由度，横移；z表示线路垂向方向自由度，浮沉；ϕ表示绕x坐标轴转动自由度，侧滚；β表示绕y坐标轴转动自由度，点头；ψ表示绕z坐标轴转动自由度，摇头。轴箱与转向架、转向架与车体之间分别由一系悬挂、二系悬挂相连，悬挂系统包含空气弹簧、减振器、横向止挡、抗扭侧杆和牵引拉杆等，均采用弹簧与阻尼器模拟。车体、转向架均具有横移、沉浮、侧滚、点头和摇头各5个自由度，由于轮对主要运动形态为滚动，故不考虑点头运动，只考虑其余4个自由度。综上，该车辆模型共考虑31个自由度。

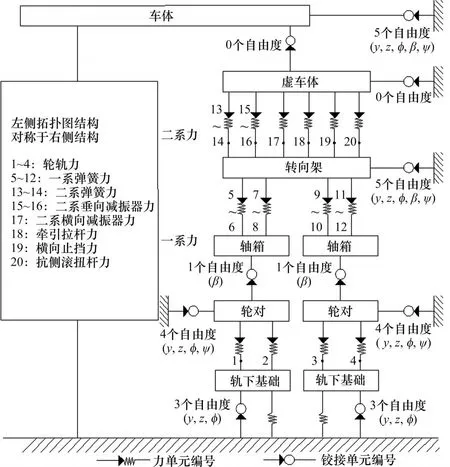
图2 车辆模型拓扑图Fig. 2 Topology of a vehicle model

1.1.2 道岔模型

根据道岔主要结构特点，对我国高速铁路18号道岔进行合理化建模，其整体模型如图3 所示。考虑到道岔尖轨、心轨截面沿纵向的渐变性特征，根据道岔图纸提取关键特征截面廓形数据，通过线性插值得到道岔各断面廓形，并结合道岔不同断面对应的里程进行排布，从而得到精细化道岔模型。尖轨与基本轨、心轨与翼轨的贴靠作用采用线性弹簧来模拟，扣件系统由线性弹簧和阻尼元件来模拟。

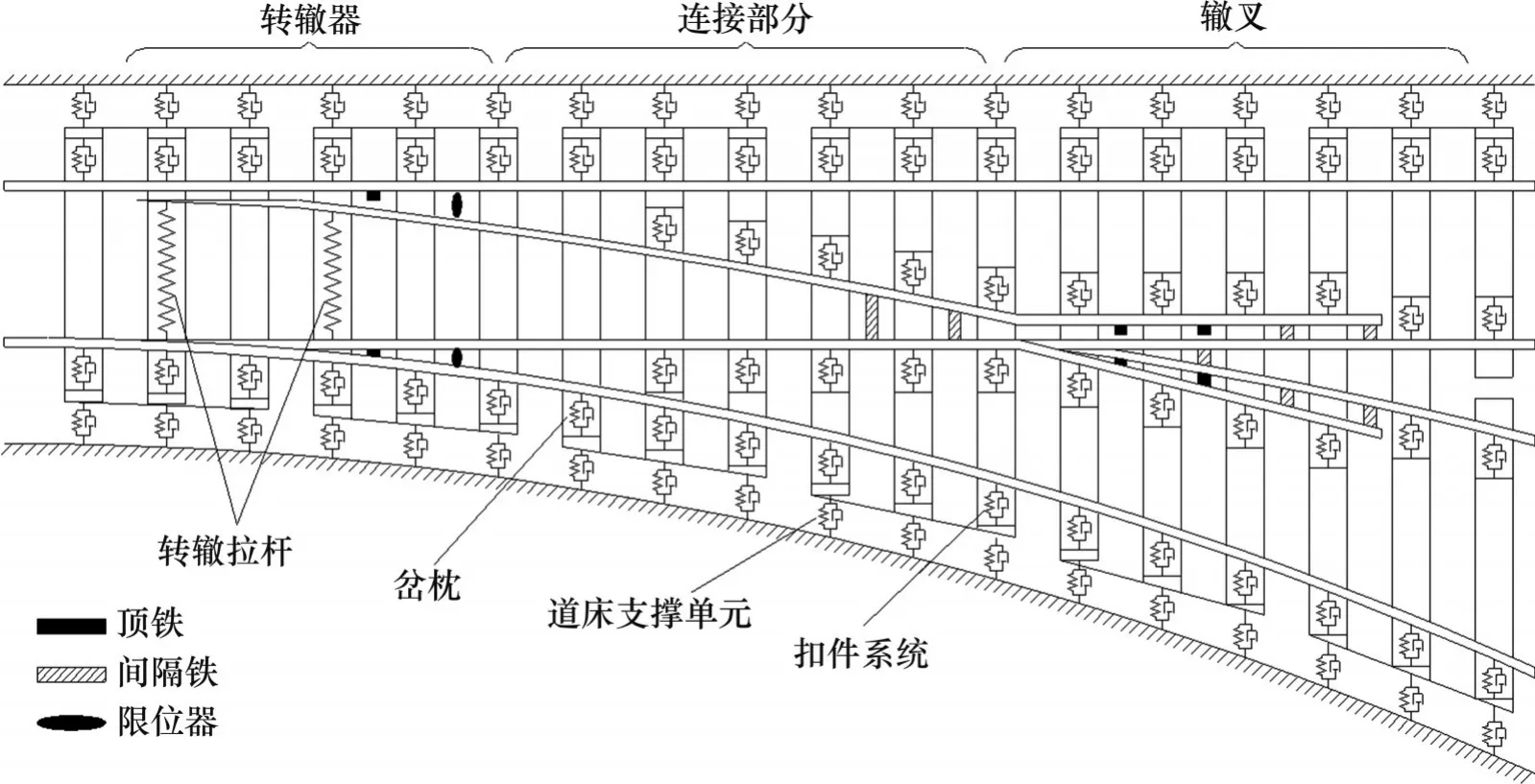
图3 道岔整体模型Fig. 3 Overall model of turnout

为充分考虑钢轨的柔性变形，本文在ANSYS中建立变截面道岔有限元模型，钢轨采用Timoshenko梁来模拟，所有钢轨节点均有6个自由度。在有限元分析中，柔性体的运动通过大量节点坐标来表示，而在SIMPACK中是用较少的模态坐标来描述物体的弹性变形。为了减少计算时间，提高计算效率，可利用Craigh-Bampton 子结构分析法缩减有限元模型的矩阵和自由度，在保留模型原有属性及计算精度的前提下求解道岔各轨件的质量矩阵、刚度矩阵以及相应的模态特征。图4所示为直尖轨的前四阶模态振型。再通过轨道配置文件定义主节点，设置弹簧刚度、阻尼的具体参数，实现道岔钢轨的柔性变形。

图4 直尖轨前4阶模态振型Fig. 4 The first 4 modal shape of straight switch rail

1.1.3 轮轨接触模型

轮轨接触模型是为了实现车辆模型与道岔模型的相互耦合，其主要涉及轮轨动态接触几何关系计算和轮轨滚动接触行为分析。其中轮轨动态接触几何关系计算主要包括轮轨接触点位置及接触角的确定，基于迹线法原理，同时考虑道岔多钢轨组合的复杂廓形进行求解；轮轨滚动接触行为分析主要是求解轮轨法向力和轮轨蠕滑力，轮轨法向力基于非赫兹接触理论进行求解，轮轨蠕滑力则根据FASTSIM算法进行计算[19]。

1.2 钢轨波磨数值模拟

图5 所示为某高速道岔钢轨表面波磨实测图。由图5 可知：该道岔区段钢轨波磨的波深为0.04 mm，波长为150 mm 左右，是一种典型的连续型谐波激扰。结合其他高速道岔波磨区段实测数据，发现其波磨的波长一般分布在120～150 mm，波深为0.04～0.10 mm。故本文采用连续的周期性余弦函数来描述其轨面不平顺，其表达式为

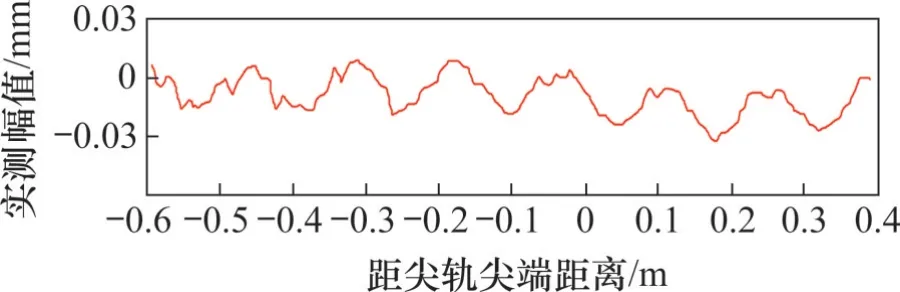
图5 某高速道岔钢轨波磨实测图Fig. 5 Measurement of rail corrugation of a high-speed turnout

式中：Zrw为钢轨表面波磨的垂向位置，mm；Ap为波磨幅值，mm；λ为波磨波长，m；xrw为钢轨的纵向距离，m；φ为初始相位角，rad。

不考虑轨道随机不平顺的作用，通过改变波磨特征参数来探究钢轨波磨对高速车辆-道岔系统动力学性能的影响规律，如图6所示。

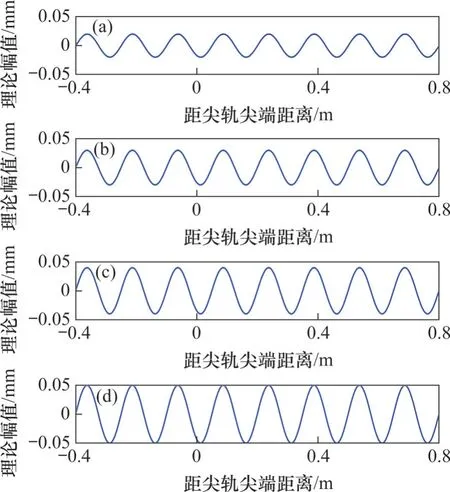
图6 波磨施加示意图Fig. 6 Schematic diagram of corrugation application

当高速列车以不同速度通过具有不同波长的钢轨波磨区段时，钢轨激励所产生的通过频率不同，可利用下式来计算：

式中：f为钢轨表面波磨激发的通过频率，Hz；v为列车运行速度，km/h。

1.3 模型验证

为了验证模型的正确性，本文对车辆-道岔刚柔耦合动力学模型进行了验证。当高速车辆以350 km/h直逆向通过道岔时，尖轨侧轮轨垂向力和轮轨横向力如图7所示，由图7可以看出：本文模型计算得到的轮轨力时程曲线最值及变化趋势与参考模型[20]的基本一致，由此证明了本文模型的可靠性。

2 结果分析

为了研究钢轨波磨对道岔区动力学性能的影响，本文基于车辆-道岔刚柔耦合动力学模型，以转辙器为例，设置不同计算工况，如表1所示。其中，波磨相位是指在道岔某一位置钢轨波磨处于波峰、波谷或它们之间某点的状态。由于道岔结构远比区间线路的复杂，当高速车辆通过无波磨道岔时，在尖轨顶宽40 mm处产生轮轨最大冲击，而在钢轨波磨与道岔结构不平顺共同激励下，该点所处的波磨相位不同时，尖轨上接触点的状态会随之改变，进而影响尖轨侧轮轨动态响应。对此，工况1选取一个周期内的4个研究点(对应相位分别为A、B、C、D)，研究尖轨顶宽40 mm 处的波磨相位对轮轨相互作用的影响，如图8所示。图8 中，A、C分别对应波磨波深时变率最大、最小的相位，B、D则分别对应波磨幅值最大、最小的相位。工况2、3、4分别探究不同波深、波长、运行速度下高速道岔钢轨波磨对轮轨动态相互作用和车辆部件垂向振动的影响。

表1 工况设置Table 1 Setting working conditions

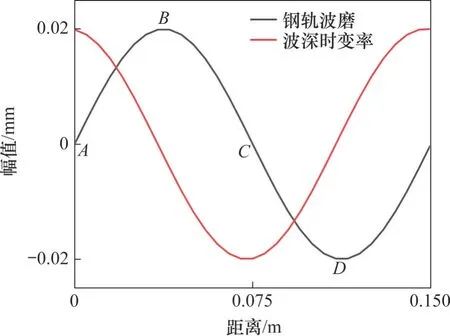
图8 波磨示意图Fig. 8 Schematic diagram of rail corrugation

2.1 波磨相位的影响

根据工况1在道岔左、右两侧钢轨设置相同的谐波波磨，其波长为150 mm，波深为0.04 mm，以此计算高速车辆以350 km/h 通过18 号客运专线道岔，钢轨波磨处于4种不同相位时的轮轨动态相互作用，如图9所示。

图9 不同波磨相位下的轮轨垂向力最值Fig. 9 The maximum of wheel-rail vertical force with different phases

由图9可见：在不同波磨状态下，基本轨侧轮轨垂向力最大值均比尖轨一侧的小，最小值均比尖轨一侧的大，说明在波磨激励下，尖轨侧轮轨垂向力上下波动幅度比基本轨侧的强烈，基本轨侧轮轨响应较尖轨侧的小。由车辆通过不同波磨相位的结果可知，基本轨侧轮轨垂向力最值在不同波磨相位下并没有明显变化，而尖轨侧轮轨垂向力最大值有明显差异，当轮轨最大冲击点处于A或B相位时，尖轨侧轮轨垂向力均比C或D相位时的大，其最小值则在A或B相位时均比C或D相位时的小。当钢轨波磨处于A相位时，尖轨侧轮轨垂向力最大值为112.11 kN，最小值为19.92 kN；当波磨B相位位于尖轨顶宽40 mm处时，尖轨侧轮轨垂向力最大值为110.70 kN，最小值为19.31 kN。因此，在尖轨顶宽40 mm 处，当钢轨波磨处于波深时变率最大的A相位时，尖轨侧轮轨垂向力最大，即对轮轨冲击影响最大。

2.2 钢轨波磨的影响

图10 所示为车辆分别通过有、无波磨情况下的尖轨测轮轨垂向力，其中图10(a)所示为无钢轨波磨时尖轨侧的轮轨垂向力，L为轮载过渡区的长度。由图10(a)可知：曲基本轨在高速车辆进入道岔之前完全承受车轮荷载；进入道岔之后，由于尖轨的分担作用，该侧轮轨垂向力缓慢减小，在距尖轨尖端距离为4.95 m 的位置开始大幅减小，直至在7.09 m 处减小为0 kN，即曲基本轨完全不承载。直尖轨则在距尖轨尖端距离为4.90 m 处开始逐渐承受车轮荷载，该侧轮轨垂向力逐渐增大，直至7.48 m 处基本不变，即直尖轨完全承受车轮荷载，完成轮载过渡。故当无钢轨波磨时，轮载过渡段的长度为2.19 m。

图10 有、无波磨情况下尖轨侧轮轨垂向力对比Fig. 10 Comparisons of wheel-rail vertical force of side of switch rail with or without corrugation

当车辆以相同速度通过波长为150 mm，波深为0.04 mm 的道岔波磨区段时，其轮轨垂向力如图10(b)所示。由图10(b)可知：直尖轨在距尖轨尖端距离为4.95 m 处开始承载，曲基本轨在距尖轨尖端距离为7.04 m 处结束承载，轮载过渡段的长度为2.09 m，较无波磨的情况缩短了4.57%。由此可知，钢轨波磨的存在会缩短轮载过渡段的长度。这是由于在轮载过渡范围内，有波磨情况下轮对向尖轨侧的横移量逐渐比无波磨情况下的小，如图11 所示，这将导致尖轨侧车轮提前从基本轨过渡到尖轨，轮载过渡段终点位置会提前。

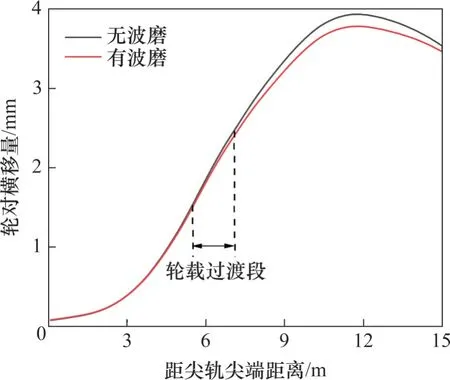
图11 轮对向尖轨侧横移量Fig. 11 Wheelset lateral displacement

当道岔钢轨波磨的波深为0.04 mm，波长为150 mm，并且尖轨顶宽40 mm 处为波深时变率最大的A 相位时，车辆以不同速度通过的轮轨力时程曲线如图12所示。结合图10和图12可知：在无道岔波磨情况下，直尖轨和曲基本轨上的轮轨垂向力在过渡段分别呈现较为平滑的增大、减小趋势；当存在道岔波磨时，直尖轨和曲基本轨上的轮轨垂向力在逐渐增大、减小的同时伴随着明显的波动，且速度越大波动幅度也越大。图12 中，当速度为200 km/h 时，轮载过渡段长度为2.36 m；随速度增大，轮载过渡段长度逐渐减小；当速度增大到400 km/h 后，轮载过渡段长度为1.94 m，较200 km/h 缩短了17.80%。图13 所示为不同速度下轮载过渡段的起始位置。由图13 可以看出：随车辆通过道岔波磨的速度越大，轮载过渡段的起始里程距尖轨尖端越远，终点里程距尖轨尖端越近，导致轮载过渡段长度越短。

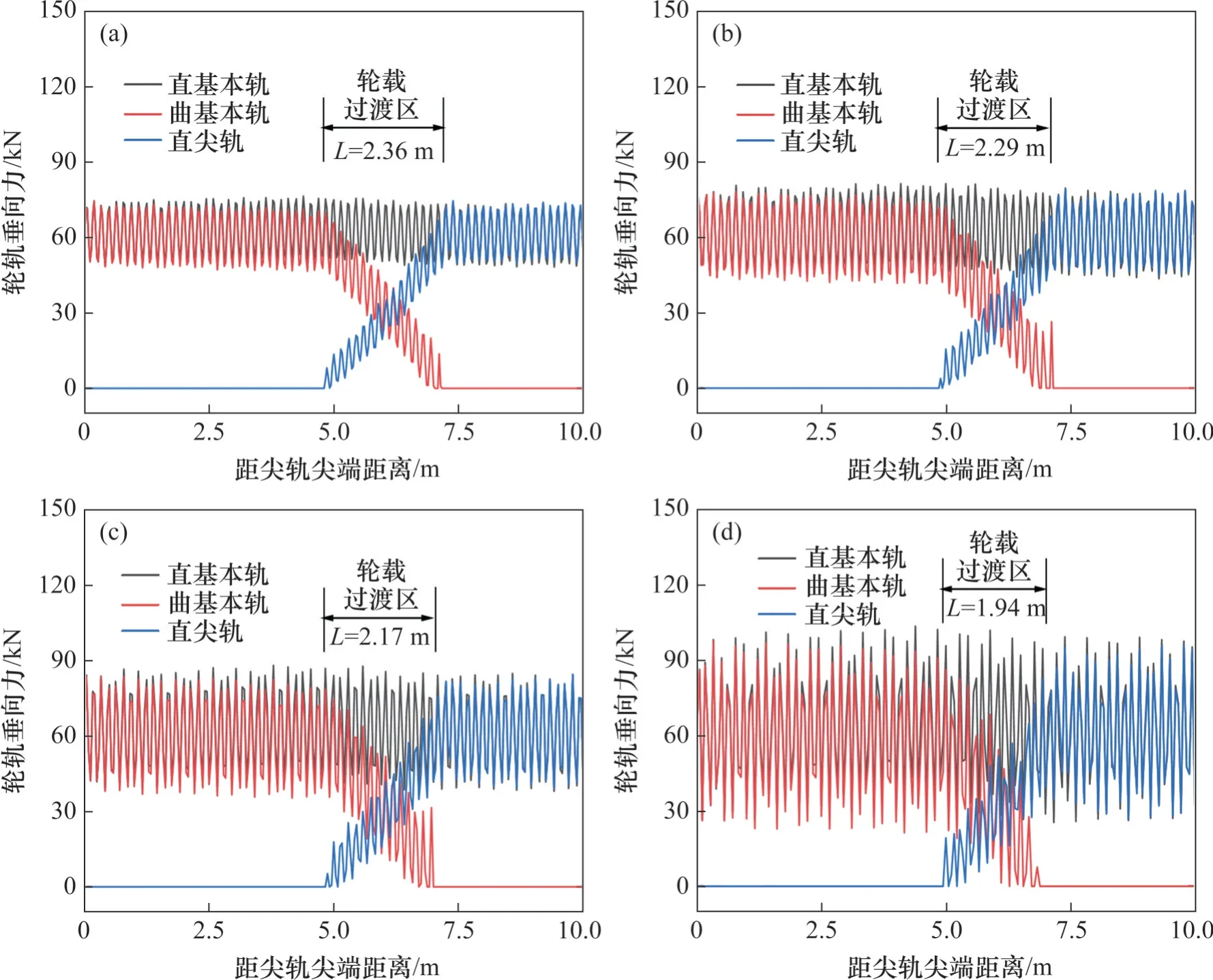
图12 不同速度下轮轨垂向力时程曲线图Fig. 12 Time history curve of wheel-rail vertical force at different speeds

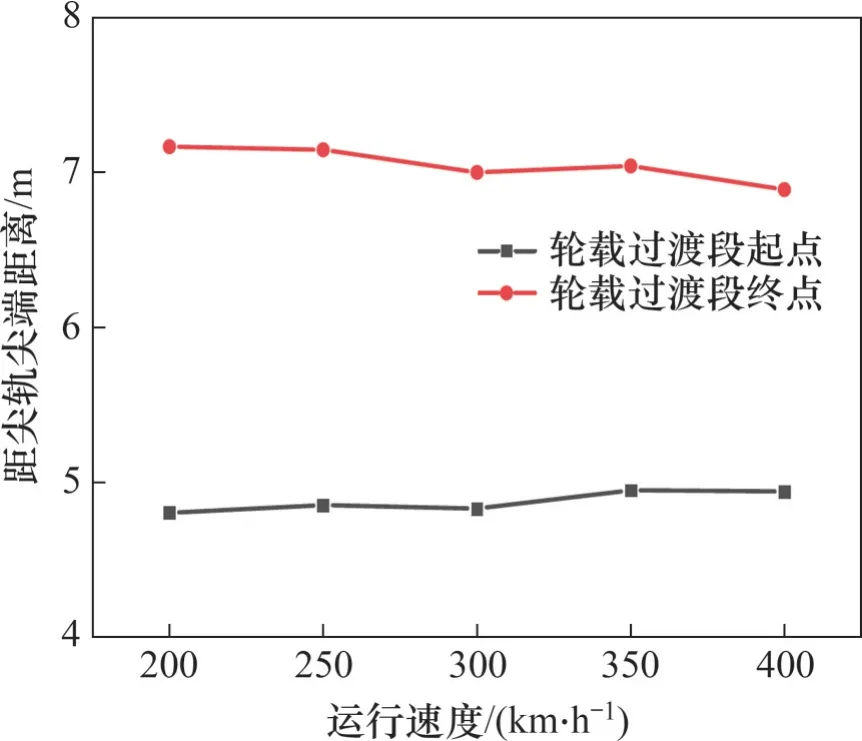
图13 不同速度下轮载过渡段起止位置Fig. 13 Starting and ending position of wheel load transition section at different speeds

2.3 波磨波深的影响

当左、右两轨全段布置波长为150 mm，并且尖轨顶宽40 mm处为A相位的波磨，车辆以350 km/h通过时，轮轨垂向力随不同波深变化的情况如图14 所示。由图14 可知：由于钢轨波磨与道岔结构不平顺的共同作用，车轮与钢轨在距尖轨尖端5～7 m的范围内产生更大的冲击。在相同波长的条件下，随波深增大，轮轨垂向力最大值不断增大，最小值不断减小，因此，尖轨侧轮重减载率会逐渐增大，对行车安全性影响也逐渐增大。当波深为0.04 mm时，尖轨侧轮轨垂向力最大值为112.11 kN，与图10 中无波磨情况下尖轨侧轮轨垂向力最大值(67.43 kN)相比增大了66.26%，这足以说明道岔波磨能够明显增大轮轨动态冲击；当波深达到0.08 mm时，尖轨侧轮轨垂向力在轮载过渡段减小至0 kN，即出现了瞬间车轮脱空的状态，危及行车安全。结合现行波磨钢轨打磨规范，当道岔区钢轨波磨波深达到0.08 mm时，此时波深已超出打磨限值[21]，并且超限百分比远比5%的验收标准大，应及时对钢轨进行打磨处理。

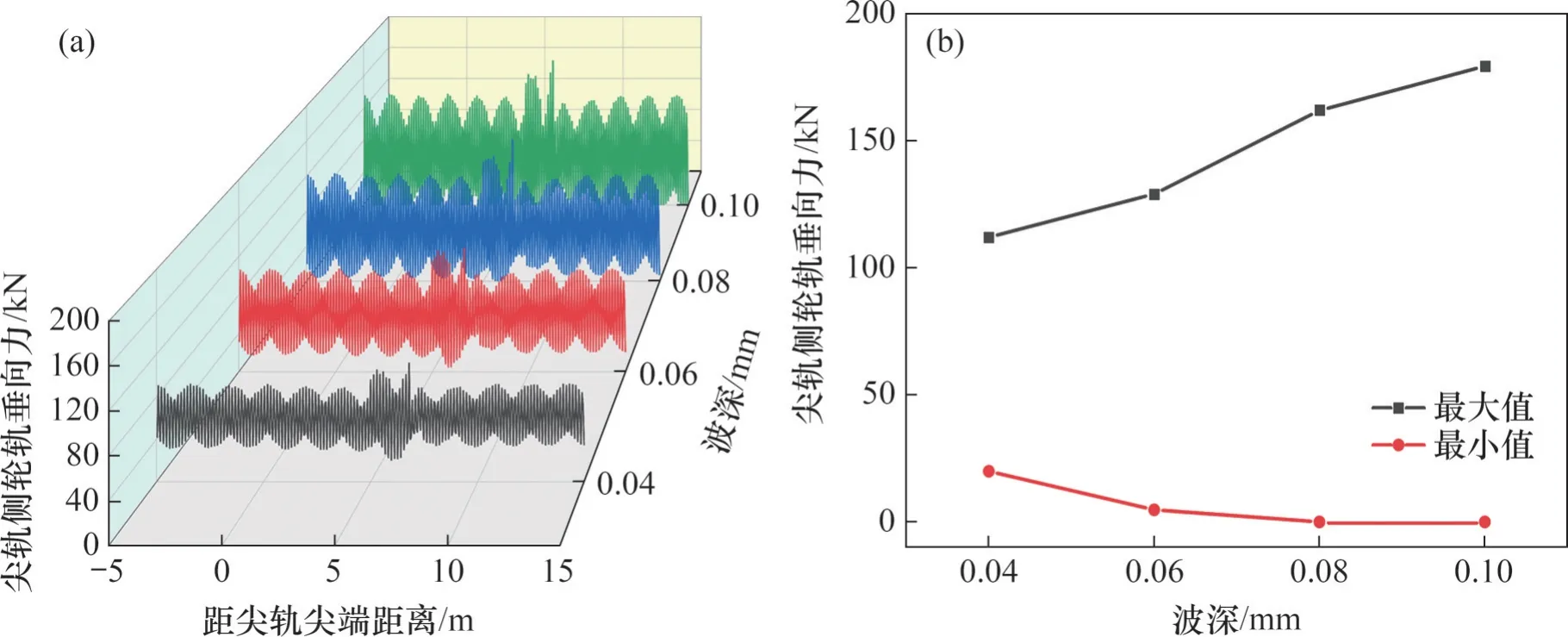
图14 不同波深下尖轨侧轮轨垂向力Fig. 14 Wheel-rail vertical forces of side of switch rail with different wave depths

当高速车辆过岔时，钢轨波磨会激发轴箱的振动，造成局部构件的疲劳损伤。图15 所示为不同波深下轴箱的垂向振动加速度曲线。由图15(a)可知：在不同波磨波深下，轴箱垂向振动加速度均在距尖轨尖端6.65 m 左右达到峰值，并且其波动的峰值与谷值出现位置均一致，说明波深的改变并不影响轴箱垂向振动的相位特征。对图15(a)里程图进行傅里叶变换，得到相应的频域图，如图15(b)所示。由图15(b)可知：不同波深下轴箱的振动主频均为648 Hz，与式(2)计算得到的激发频率基本一致。当波深从0.04 mm 增大至0.06、0.08和0.10 mm 时，轴箱垂向振动幅值分别增大了47.58%、93.37%和133.00%。综上可得，在波长相同的情况下，随着波磨波深不断增大，轴箱垂向振动加速度不断增大。

图15 不同波深下轴箱垂向振动加速度Fig. 15 Axle box vertical vibration acceleration with different wave depths

2.4 波磨波长的影响

为研究不同波长的影响，取波长分别为120、130、140 和150 mm，波深为0.04 mm，且尖轨顶宽40 mm 处均为波磨A相位，当高速车辆以350 km/h 通过道岔时，尖轨侧轮轨垂向力如图16所示。由图16可知：当波长为120 mm时，尖轨侧轮轨垂向力最大值为123.47 kN；当波长为150 mm时，尖轨侧轮轨垂向力最大值为112.11 kN，较波长为120 mm 时减小了9.20%。可以看出，在相同波深的条件下，随波长增大，尖轨侧轮轨垂向力不断减小，轮轨垂向力波动幅度也不断减小，车辆过岔的轮轨冲击逐渐趋于平稳。

图16 不同波长下尖轨侧轮轨垂向力Fig. 16 Wheel-rail vertical forces of side of switch rail with different wavelengths

图17(a)所示为不同波长下轴箱的垂向振动加速度里程图，对其进行傅里叶变换，得到对应的频域图，如图17(b)所示。利用式(2)计算得到不同波长下所激发的振动频率，如表2 所示。由图17和表2可以看出：不同波长下轴箱的垂向振动加速度均在轮载过渡范围内明显增大，这是由道岔结构不平顺引起的。不同波长波磨激发的振动频率不同，且与理论计算的振动频率一致，说明轴箱的高频振动是由钢轨波磨激励造成的。当波长为120 mm时，轴箱在810.19 Hz下的垂向振动幅值最大，达18.56 m/s2；随波长逐渐增大，其振动幅值逐渐减小；当波长增大至150 mm 时，轴箱在648.15 Hz下的垂向振动幅值最小为12.82 m/s2，较波长为120 mm时减小了30.93%。这说明在波深不变的情况下，轴箱的垂向振动加速度随钢轨波磨波长的增大而减小。

表2 速度350 km/h、波深0.04 mm下不同波长钢轨波磨激发的振动频率Table 2 Vibration frequencies excited by rail corrugation at different wavelengths at 350 km/h and wave depth of 0.04 mm

图17 不同波长下轴箱垂向振动加速度Fig. 17 Axle box vertical vibration acceleration with different wavelengths

2.5 通过速度的影响

为研究不同通过速度的影响，当波磨波长为150 mm、波深为0.04 mm、尖轨顶宽40 mm 处为波磨A相位时，尖轨侧轮轨垂向力分布如图18 所示。由图18 可知：当运行速度为200 km/h 时，在轮载过渡段轮轨垂向力出现幅值，即最大值为81.41 kN，最小值为41.76 kN。随过岔速度增大，尖轨侧轮轨垂向力最大值逐渐增大，最小值逐渐减小。当速度达到400 km/h 时，轮轨垂向力最大值达到116.44 kN，最小值达到13.93 kN，分别较200 km/h 时增大了43.03%，减小了66.64%。由此可得，尖轨侧轮轨垂向力随速度增大而逐渐增大。

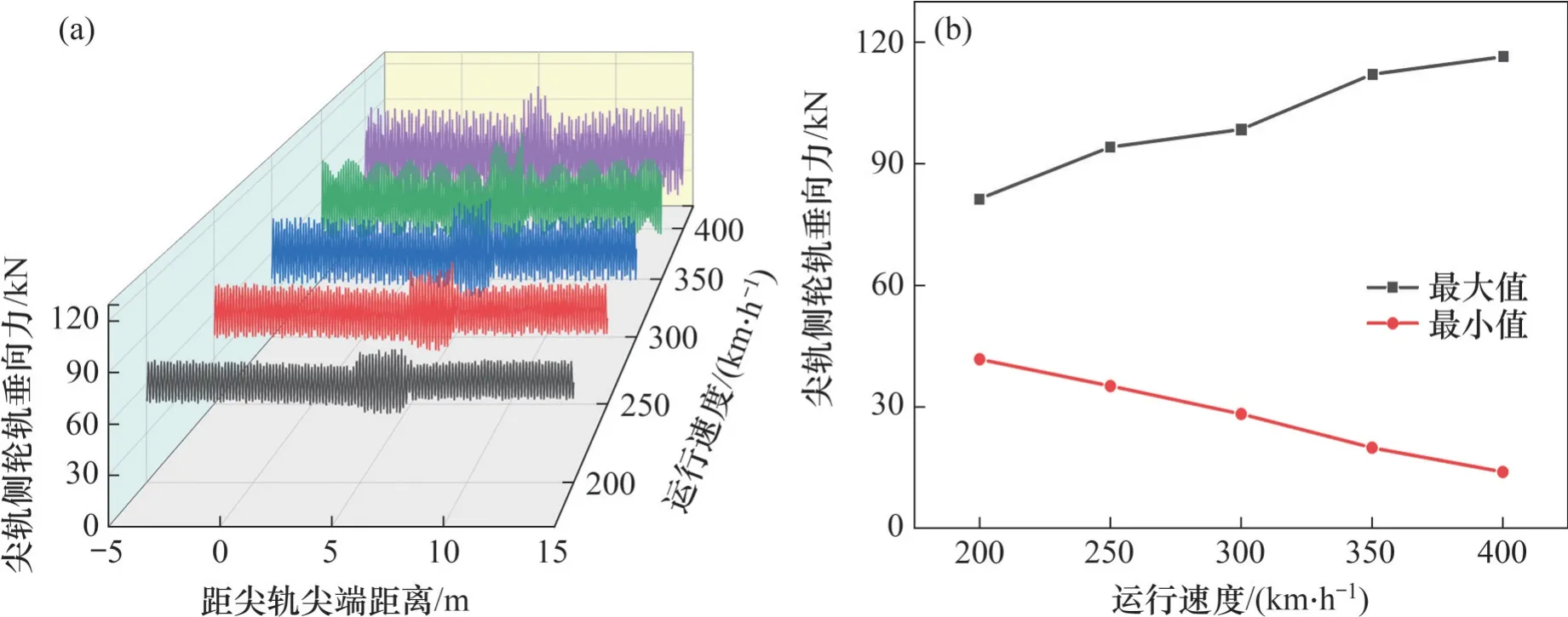
图18 不同速度下尖轨侧轮轨垂向力Fig. 18 Wheel-rail vertical forces of side of switch rail at different speeds

不同速度下轴箱的垂向振动加速度如图19 所示。由图19 可以看出：随速度增大，轴箱垂向振动加速度的波动幅度增大。车辆通过道岔波磨区段时轴箱会产生高频振动，尤其在轮载过渡段振动幅值会增大。此外，在相同的钢轨波磨特征下，随速度增大，波磨激起的主频不断增大，与表3计算得到的通过频率相符。根据显色卡的刻度也可以看出，速度越大，轴箱的垂向振动加速度越大，对应主频的频带宽度也逐渐增大。

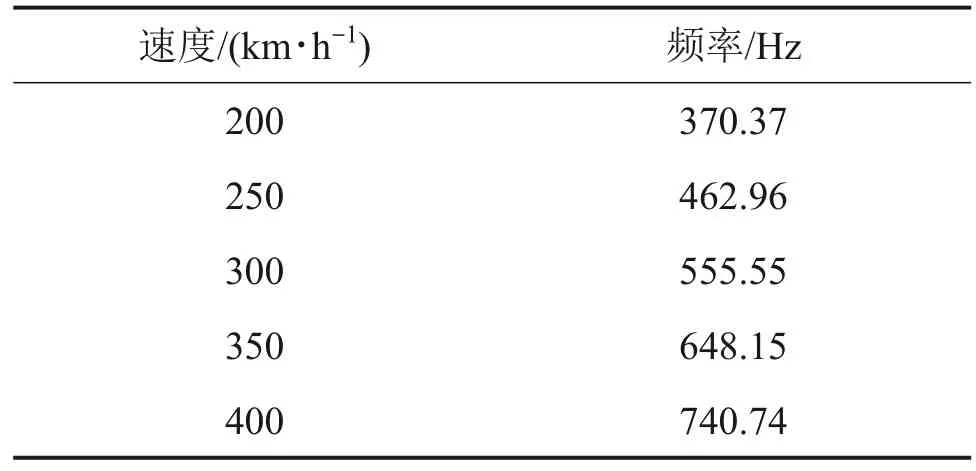
表3 波长150 mm、波深0.04 mm下不同速度钢轨波磨激发的振动频率Table 3 Vibration frequencies excited by rail corrugation at different speeds at wavelength 150 mm and wave depth of 0.04 mm

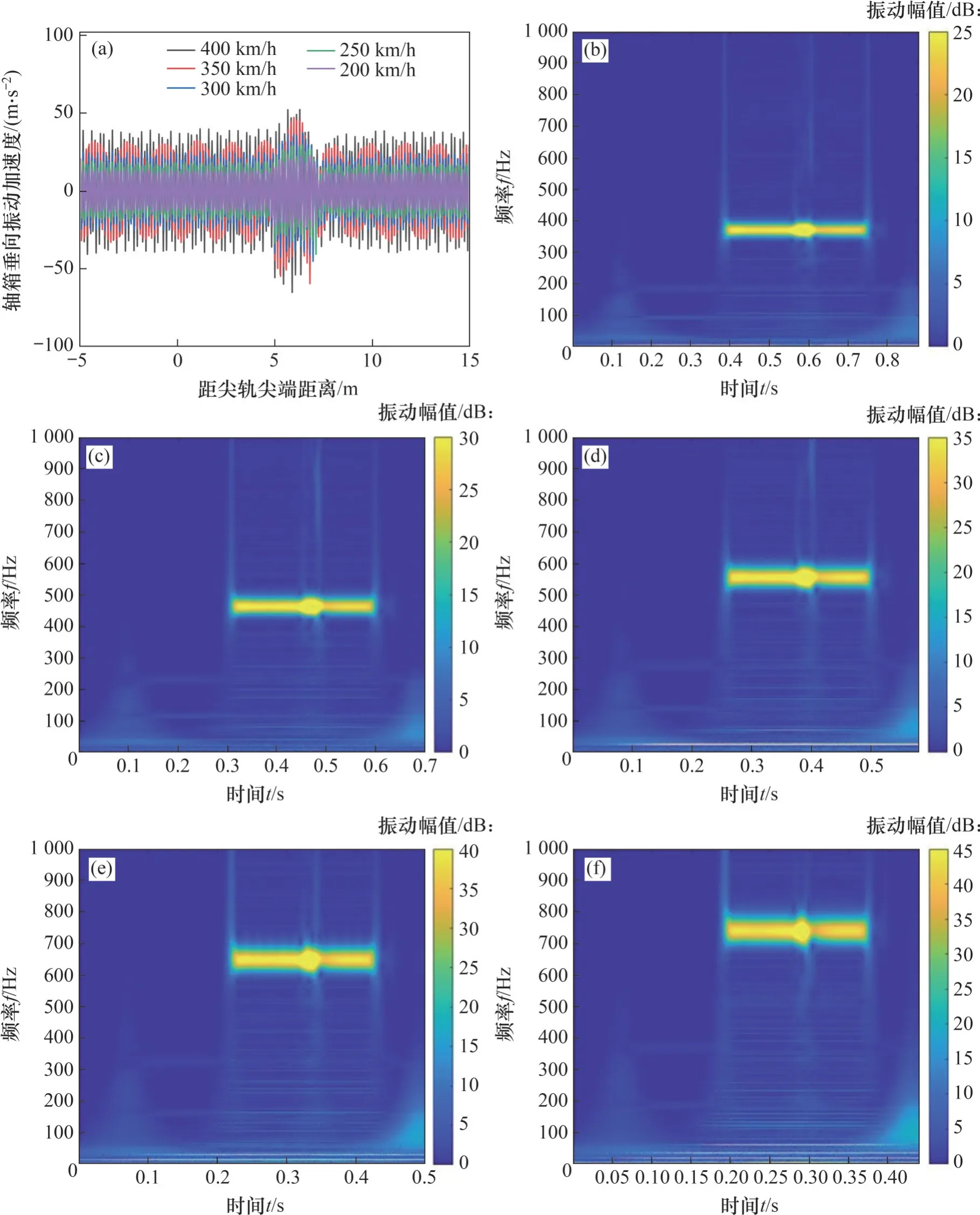
图19 不同速度下轴箱垂向振动加速度Fig. 19 Axle box vertical vibration acceleration under different speeds

3 结论

1) 当钢轨波磨的分布相位不同时，车辆通过道岔的轮轨动态响应存在差异。其中在尖轨顶宽40 mm处，波磨处于波深时变率最大相位时的轮轨垂向力最大，处于幅值最小相位时的轮轨垂向力最小。

2) 高速道岔钢轨波磨对轮载过渡有一定影响。钢轨波磨的存在会导致轮载过渡段缩短4.57%，加剧轮轨垂向力的波动，影响高速车辆通过的平顺性；且随速度增大，轮载过渡段的长度不断缩短。

3) 高速道岔钢轨波磨能明显增大轮轨动态相互作用，且波磨波深越大，运行速度越快，波磨波长越短，尖轨侧轮轨垂向力越大。当波长为150 mm，波深达到0.08 mm 时，尖轨侧轮轨垂向力在轮载过渡段减小至0 kN 时出现瞬间轮轨分离现象，影响行车安全。

4) 高速道岔钢轨波磨会引起轴箱持续振动，其垂向振动加速度幅值与波深、通过速度呈正相关，与波长呈负相关，且最大值均出现在轮载过渡段。因此，可以通过测量车辆轴箱垂向振动加速度来检测与评估道岔区波磨。