融合RRT-Connect和DWA算法的室内移动机器人单目标点导航任务研究

王冠强 ，张驰洲, ，陈明松, ，蔺永诚 ，邹奋扬 ，王秋, ，吴敏杰 ，曾维栋

(1. 中南大学 机电工程学院，湖南 长沙，410083；2. 极端服役性能精准制造全国重点实验室，湖南 长沙，410083；3. 中南大学 轻合金研究院，湖南 长沙，410083)

路径规划技术是移动机器人领域的一项热门研究[1-2]。路径规划的最终目的是寻找到一条可以从起始点到目标点的无碰撞路径[3-4]。根据对环境信息的掌握程度不同，路径规划方法可分为全局路径规划和局部路径规划。全局路径规划方法是在已知的地图环境下，规划出一条无碰撞的最优路径；而局部路径轨迹规划是在地图环境信息完全未知或部分可知下，侧重于考虑机器人当前的局部环境信息，让机器人规划出一条能够动态避障的局部路径[5-6]。在路径规划中面临的问题有搜索节点数冗余、搜索方向不明确和搜索时间长等[7-8]，因此亟需设计合理的规划器解决上述问题。

针对全局路径规划问题，传统的路径方法有RRT 算法、BFS 算法和A*算法[9]等。当地图环境较大或者复杂时，使用BFS 和A*算法的规划效率往往不如RRT 算法的规划效率[10]。RRT(rapidexploring random tree，快速搜索随机树)算法首先由LAVALL[11]提出，该算法是以路径起点为根节点，从空闲区域选取随机节点引导树的生长方向，当树中的叶子节点扩散到目标点，完成整个搜索过程[12]。但是，该算法也存在诸多不足，如RRT算法的随机采样思想导致节点扩展无目标导向性，容易出现大量冗余节点，算法的收敛速度过慢[13]。同时路径存在着转折次数过多，路线不平滑、与障碍物安全距离过小和最大转角过大等不符合车辆运动学要求的问题[14]。因此，针对上述问题，许多学者展开了系列研究。KUFFNER等[15]提出了RRT-Connect算法以提高收敛速度，但在复杂环境中该方法采样范围不确定和随机性过大[16]。KANG等[17]提出了一种基于三角不等式RRT-Connect机器人路径规划算法，减少了规划时间和路径长度。韦玉海等[18]提出了一种AMRRT-Connect 算法以解决移动机器人在狭隘与复杂环境中非完整性约束问题。

针对局部路径规划问题，常用的方法有DWA、人工势场法和时间弹性带算法等。其中，人工势场法在机器人与障碍物相近时无法生成路径，时间弹性带算法面对较为动态的场景时获得的最优路径会频繁变化。相比之下，DWA 算法更符合机器人的控制行为。DWA是FOX等[19]提出的一种局部路径规划方法，主要是在速度空间中进行速度采样，并预测出这些速度在一定时间内的运动轨迹，随后通过评价函数对预测轨迹进行评价，选取最优轨迹对应的速度空间用以驱动机器人运动。郭烈等[20]提出了一种融合PID 控制的TEB 算法，减小了控制指令的波动范围。ZHANG等[21]采用以目标距离代替DWA算法中方向角差的评价项，避免路径因振动而不平滑。目前，DWA 算法所预测的轨迹在离障碍物较近时才开始避障，因此，往往需要结合其他避障算法进行优化。

综上，伴随着移动机器人的发展，全局路径规划算法与局部路径规划算法得到了广泛研究，但仍然存在不少问题而导致规划的路径质量不佳或效率不高。针对以上问题，本文作者提出一种人工势场法与RRT-Connect算法相结合的全局路径规划算法，并针对移动机器人实际运行需求，对改进算法规划出的路径进行后处理，大幅度提高了输出路径的质量。同时为了提高机器人的动态避障能力，提出改进的DWA 局部路径规划算法，最终实现移动机器人在室内环境下的自主路径规划任务。

1 路径规划算法

全局路径规划要解决的首要问题是如何为机器人找到起点到目标点的可通行路径，虽然在这个过程中还会构建一系列优化目标，包括路径最短、提前躲避障碍物等等，但是最关键的是获得路径的基本信息。机器人只有在全局路径规划算法下确定了路径信息后，局部路径规划算法才会在局部范围内不断更新其自身的运动信息，从而完成路径规划的全部任务。

1.1 改进RRT-Connect算法的全局路径规划方法

在全局路径规划方法的开发中，RRT-Connect算法由于在RRT 的基础上引入了双树扩展环节而得到了广泛的推广使用。该方法分别以起点和目标点为根节点同时扩展随机树，从而实现对状态空间的快速搜索。然而，其灵敏度和实时性仍存在着较大的不足。此外，RRT-Connect算法由于采样点选取范围过广，在采样过程中会存在随机性过大的问题。因此，本节以RRT-Connect算法为基础进行系列开发与研究，拟改善上述不足，推动全局路径规划算法的优化，如算法1 所示。首先，提出增设第三、第四棵扩展树生成两个RRTConnect 扩展区域进行扩展的方式，实现算法搜索效率和速度的提升。其次，提出以起点和终点所在矩形区域为采样点限定选取范围的方式，减少不必要扩展，加快算法收敛速度。最后，为减少RRT-Connect算法中节点选取的随机性，引入人工势场法用于引导扩展随机树朝着目标点进行启发式扩展。在算法1 中给出了改进后的RRT-Connect整体流程。

1.1.1 增设第三和第四扩展树

为了能够增加第三和第四棵扩展树，同时生成两个RRT-Connect扩展区域，提升算法的搜索效率，首先应选取合适的第三和第四棵扩展树的根节点坐标，本文取起点pstart(缩略为ps，下同)与终点pgoal(pg)连线的中点为第三根节点pcentral(pc)，同时以点pc为圆心，步长为半径作圆弧与直线pspg相交，取靠近终点pg的交点为pcentral_r(pcr)，也即第四根节点。设起点坐标为ps(xs，ys)，终点坐标为pg(xg，yg)，则第三根节点与第四根节点的坐标计算公式为：

算法1：改进后的RRT-Connect输入：起始点pstart，目标点pgoal，障碍物点pobstacle输出：路径Path(pstart，pgoal)1：按照式(1)和(2)计算pcenter，pcenter_r；T1.init(pstart)，T2.init(pcenter)，T3.init(pcenter_r)，T4.init(pgoal)//初始化2：Cr←Sampling_Area_Limitation(pstart，pgoal)3：for i=1 to n do 4：pnew1 ∈ Cr←Sampling_GRAR(pstart，pcenter，pobstacle，prand1)pnew2 ∈ Cr←Sampling_GRAR(pcenter_p，pgoal，pobstacle，prand2)if Extend (T1，prand1)≠Trapped then 5：6：7：8：9：10：11：12：13：14：15：16：17：18：19：end 20：return Fail 21：//函数Extend( )和Connect( )的实现基于文献[12]22：//函数Sampling_Area_Limitation( )表示限定采样点生成范围23：//函数Sampling_GRAR( )是指在引力场和排斥场的作用下产生随机点if Connect (T2，pnew1)=Reached then Path1=Path(T1，T2)end Swap(T1，T2)end if Extend (T3，prand2)≠Trapped then if Connect (T4，pnew2)=Reached then Path2=Path(T3，T4)end Swap(T3，T4)end return Path=Path.push(Path1，pcenter，pcenter_p，Path2)

同时，考虑到中点pc可能位于障碍物中的情况，采取中点偏置的方法，即当中点位于不可达区域时，以pc为圆心，在步长r为半径的圆内搜索可达点pfree(pf)，用于替代中点pc，从而实现增加第三和第四根节点的目的。

1.1.2 限定采样点选取范围

在RRT-Connect算法中，存在许多随机生成的扩展节点，而其中的大部分节点属于无效节点，不参与组成最终路径，但是生成这些节点会增加算法的总体时间成本。因此，为提升算法收敛速度和效率，减少迭代运算次数和无效节点，以更少的时间和更小的内存需求找到最佳路径，本文以起点ps和终点pg所在区域为限定采样区域Cr，采样区域的确定原则为以起点ps与终点pg间连线斜率k为基础，取斜率为且经过起点ps与终点pg的两条直线与地图边界的交点分为Q1、Q2、Q3、Q4，连接这四个点所组成的矩形封闭区域为限定采样区域，如图1所示。当在自由空间C中随机选取采样点prandom(pran)时，若所选采样点pran∈Cr，则保留为采样点。反之，则删除此点，取终点pg为本次扩展采样点进行迭代运算。若在限定采样区域Cr中无法搜索到可行路径，则采取增大Q1与Q2、Q3与Q4坐标直线距离的方式扩大限定采样区域，直到找到可行路径。通过设立上述矩形限定采样区域，使得无效采样点数量大幅度减少，提高了扩展效率，缩短了总体时间成本。

图1 矩形采样区域示意图Fig. 1 Schematic diagram of rectangular sampling area

1.1.3 引入人工势场法

RRT-Connect算法在节点搜索时的随机性导致节点对大量无效空间扩展，为此，本节将人工势场法[22]引入至上述改进的RRT-Connect算法中，用于引导扩展随机树朝着目标点进行启发式扩展。同时，选取合理斥力距离和系数，避免了与障碍物发生碰撞，提高了算法的安全性和实时性。具体地，在RRT-Connect算法的扩展节点上分别叠加一个引力场和斥力场去引导随机节点的产生方向。叠加引力场和斥力场后的算法核心思想就是在任一个双向扩展随机树中的单个节点n都增加一个目标引力函数A(n)和目标斥力函数R(n)，此时的n节点表示由根节点向外扩展的第n个新节点，扩展方式为

式中：F(n)为新节点到目标点的扩展函数；G(n)为新节点的随机扩展函数；A(n)为目标点到随机树中最近节点pnear(pne)的引力函数；R(n)为障碍物点到随机树节点的斥力函数。

新节点的随机扩展函数G(n)的表示方法为

式中：λ为扩展的固定步长。

目标引力函数A(n)和斥力函数R(n)的表示方法为

式中：ε和γ分别为引力系数和斥力系数；‖xg-xne‖为目标点到随机数中最近点的欧式距离；‖xo-xne‖为障碍物点到随机数中最近点的欧式距离；E(xg，xne)为目标点到随机数中最近点的方向向量；E(xo，xne)为障碍物点到随机数中最近点的方向向量。

由以上公式得到叠加了引力场和斥力场的新节点生成方法如下：

叠加了引力场后的新算法每一个节点的扩展都是按照式(7)的方法进行，使两棵双向随机树在各自引力和斥力分量的引导下向目标点方向扩展，扩展示意图如图2所示。

图2 在引力场和斥力场下节点扩展示意图Fig. 2 Schematic diagram of node expansion under gravitational and repulsive fields

1.1.4 路径平滑处理

对于RRT 系列算法，最终路径是通过连接各扩展点来确定的。然而，由于各点之间连线是直线段，所以最终路径是由许多段直线组成，呈不规则折线状。这样的路径不符合移动机器人的运行要求。因此，本节提出引入Dijkstra 算法[23]进行路径节点筛选，通过筛选路径中的关键节点，去除不必要节点，使得路径节点数大幅度减少，增加了路径平滑度，如图3所示。

图3 节点筛选示意图Fig. 3 Schematic diagram of node screening

同时考虑到机器人的转向能力，期望最短的欧几里得距离分布和较低的轨迹平滑度。基于以上分析，本文选择一个更合理的成本函数Cost，如式(7)所示。图4所示为成本函数的节点示意图。

图4 改进成本函数的节点示意图Fig. 4 Node diagram of improved cost function

式中：pi和pj表示一对相邻节点；‖pij‖表示相邻节点的欧式距离；θij表示两个相邻节点的相对航向角；Normal表示归一化；ω1和ω2分别表示距离和航向角的权重系数。

通过上述改进的RRT-connect 算法可获得移动机器人在固定空间下的平滑全局移动路径。然而，该路径并不能作为最终的机器人移动轨迹。这是由于平滑后的路径可能存在过平滑的现象以及平滑后路径上存在障碍物。此外，该路径上突然引入新障碍物，即面对未知空间，机器人依旧无法准确通行。因此，在全局路径规划的基础上，还需结合局部路径规划算法进行路径的实时调优。

1.2 改进DWA算法的局部路径规划算法

为更好地扩展机器人在移动过程中的实时调优能力，本节将介绍移动机器人的实时轨迹计算方式，并基于DWA算法进行评价函数优化以加快函数收敛速度，减少路径计算耗时，实现更快速的动态决策。

1.2.1 机器人航迹推算

本文中所研究的两轮差速移动机器人运动学分析如图5 所示(图5 中：vc和wc分别为底盘中心点oc的线速度和角速度；x(t)、y(t)和θ(t)分别为当时时刻机器人的横坐标、纵坐标和偏航角)。其中底盘有三个车轮，两个后轮为驱动轮，分别由独立的直流伺服电机来进行驱动，为移动机器人的运动提供动力；前轮为万向轮，主要负责稳定车体并保持平衡。

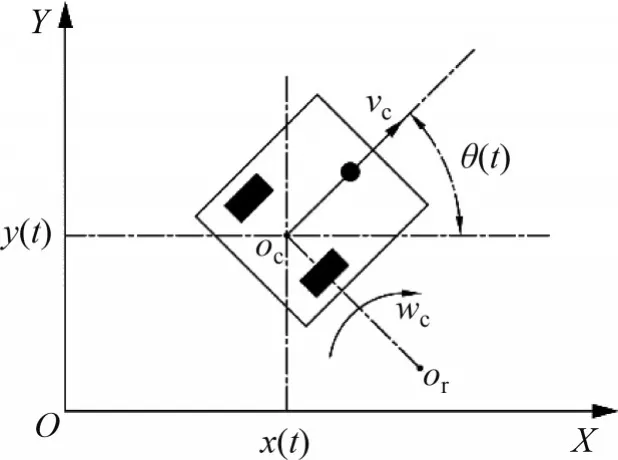
图5 两轮差速移动机器人运动学模型图Fig. 5 Kinematic model diagram of two wheel differential mobile robot

假设机器人整个运动过程匀速行驶，经过很小的时间间隔Δt后(近似轨迹直线处理)，其航迹推算公式如下：

由式(9)可知：对于任意t时刻机器人的位姿，都可以通过速度集合(vc，wc)推算出采样周期Δt内的位移位姿及其运动轨迹。而DWA算法作为一种简单高效的算法，通过对机器人的速度矢量空间进行采样，再评价产生轨迹的好坏以确定最佳轨迹，在差速移动机器人研究领域得到了广泛使用。而为了进一步提高算法的高效性，接下来对DWA中的评价函数进行优化。

1.2.2 评价函数优化

在运动过程中，原轨迹评价函数中的角度差评价函数会选择角度差值较小的速度集合来进行角度修正，这样也会使得移动机器人需要进行反复的角度调整。因此，这里引入目标点距离评价函数替代航向角函数，以预测轨迹中离目标点最近的轨迹作为下一时刻的最优轨迹，改进后的新评价函数如下式所示：

式中：GD(vc，wc)表示当移动机器人速度集合为(vc，wc)，地图中的障碍物与移动机器人车体中心的最短距离；Do(vc，wc)主要用于筛选出能使移动机器人规避地图中障碍物的轨迹，保证运动安全；V(vc，wc)是在满足上述两个筛选条件的前提下，尽量选出当前速度集合中较大的角速度与线速度，保证移动机器人能够以较快的速度运行；α、β、γ分别为轨迹评价函数三个性能指标的权重系数；GD(vc，wc)为距离评价函数，主要用于获取当前时刻下移动机器人的速度空间中各个速度集合所对应的轨迹末端终点与目标点之间的欧式距离，其计算公式如下：

式中：g(x)与g(y)分别为目标点的横坐标与纵坐标；xt(x)与xt(y)分别为当前时刻下预测轨迹末端的横坐标与纵坐标。GD(vc，wc)通过依次对比各个速度集合(vc，wc)所对应的预测轨迹末端与目标点之间的距离，取距离目标点最近的轨迹为最优轨迹，不需要反复进行角度调整，加快了算法收敛速度。

2 单目标点导航算法

由于全局和局部路径规划都有各自的缺陷，RRT-Connect算法可获取全局范围内的最佳路径却无法躲避动态障碍物，DWA 算法能躲避动态障碍物却容易陷入局部最优。鉴于此，本文以改进RRT-Connect算法规划的全局路径为指引，融合改进评价函数的DWA算法实现移动机器人的动态避障，从而实现安全有效的单目标点导航任务。单目标点算法流程图如图6所示。

图6 单目标导航算法流程图Fig. 6 Flow chart of single target navigation algorithm

3 实验与分析

3.1 仿真实验

仿真实验硬件平台配置为AMD Ryzen 5 3600 6-Core Processor 3.59 GHz CPU，RAM 为16 GB，采用matlab2020a软件平台编程实现。

3.1.1 改进RRT-Connect算法仿真对比实验与分析

为了证明本文所提出的全局路径规划算法可行性与稳定性，本仿真实验基于长度×宽度为640 m×600 m 的二维环境地图进行。图7 和图8 所示分别为简单环境和复杂环境效果对比图。图中，白色区域为可通行区域，黑色区域为不可通行区域。仿真实验中起点ps坐标为(20，20)，终点坐标pg为(580，580)，结合文献[24]设置各项参数λ=20、ε=1、γ=20、ρ0=120、P=20。同时，对比改进RRT-Connect 算法与传统RRT 算法、RRTConnect 算法在相同环境中规划出的路径长度和运行时间，如表1所示。

图7 简单环境效果对比图Fig. 7 Performance comparison of diverse algorithms under complex environment

图8 复杂环境效果对比图Fig. 8 Performance comparison of diverse algorithms under complex environment

由图7 和8 及表1 可知：在简单环境中，与传统的RRT算法和RRT-Connect算法相比，改进后的RRT-Connect 算法的全局路径长度分别减少了311 m 和142 m，算法运行时间分别减少了29.37 s和3.36 s。即改进RRT-Connect 算法路径长度最高缩短了27.3%，运行时间最高缩短了92.88%。而在复杂环境中，与传统的RRT算法和RRT-Connect算法相比，改进后的RRT-Connect算法所获得的全局路径长度分别减少了297 m 和236 m，算法运行时间分别减少36.12 s和3.74 s。即路径长度最高缩短了26.92%，运行时间最高缩短了89.78%。

此外，改进后的RRT-Connect算法进行了路径节点筛选，解决了输出路径折线段和转角过多的问题，因此，所规划的路径质量显著比传统的RRT 和RRT-Connect 算法的优。改进后的RRTConnect 算法规划出的路径长度和运行时间均明显比传统的RRT算法和RRT-Connect算法的少。

3.1.2 融合算法仿真对比实验

1) 确定最优评价函数权重参数。为了验证融合算法的有效性，需要对局部规划器(改进DWA算法)评价函数的参数进行整定，其中权重参数有α，β和γ，设置了如图9所示的二维仿真环境地图，该环境地图长度×宽度为12 m×12 m，其中白色圆圈所在区域代表此处为障碍物区域，起点坐标为(0，0)，终点坐标为(10，10)。对目前繁琐的反复调参情况，本文选用待定系数法，先取GD(v，w)的权重系数α为经验值0.5，通过设置以下实验参数对照组，以运行时间最短为评价标准，选取最优的参数β和γ。

图9 二维仿真场景示意图Fig. 9 Schematic diagram of two-dimensional simulation scene

α为0.5 时不同权重参数组合的路径规划耗时结果如表2 所示。由表2 可知：当γ为0 时，DWA算法不考虑轨迹评价函数V(v，w)的约束效果，此时由于移动机器人没有前行速度参考，所以会出现时间t无穷大而导致规划失败的情况，无法进行有效的局部路径规划。当β和γ分别为0.1 和0.9时，移动机器人局部路径规划所用的时间t最短。

表2 α为0.5时不同权重参数组合的路径规划耗时结果Table 2 Time-consuming results of path planning with different weight parameter combinations when α is 0.5 s

2) 动态避障测试实验对比。为验证融合算法的动态避障能力，使用长度×宽度为20 m×20 m环境地图作为仿真实验环境，设置起始点坐标为(1，1)，目标点坐标为(19，19)，在改进融合算法规划的路线上添加2个动态障碍物A和B，融合方法验证结果如图10所示。其中第一个动态障碍物A和第二个动态障碍物B分别以v=1 m/s的速度沿x轴负方向和y轴方向从a和b点移动至a′和b′点，虚线空心椭圆框为机器人与障碍物相遇时障碍物的位置。机器人参数反馈如图11所示。

图10 存在动态障碍物时的融合算法仿真实验Fig. 10 Simulation experiment of fusion algorithm under dynamic obstacle avoidance

图11 融合算法机器人线速度和角速度输出结果图Fig. 11 Robot linear and angular velocities of fusion algorithm

从图10 可知：改进后的路径规划算法所规划的路径能够有效避开动态障碍物，且与障碍物之间始终保持安全距离。由图11 可知：在与障碍物相遇时，融合算法能够降低机器人的线速度，当避开障碍物时恢复最大移动速度，有效避免了与动态障碍物相碰的情况。

3.2 物理实验

为验证融合导航算法在真实环境中的动态避障效果，使用两轮差速移动机器人Turtlebot2 进行实验。其中，机器人具体结构如图12(a)所示，真实实验场地如图12(b)所示。以个人PC为主机、机器人控制器为从机进行局域网内主从机网络配置。其中，主机端开启键盘控制节点，而从机端开启基于Gmapping算法的建图节点，构建如图12(c)所示的栅格地图。在机器人上搭载的主要器件有：1个STM32F103 运动控制器、4 个驱动电机、1 个Ls01b型激光雷达等，同时在机器人控制器和个人PC中预装基于Ubuntu18.04的机器人操作系统ROS(Melodic)。

图12 室内实验条件Fig. 12 Indoor experimental conditions

3.2.1 改进RRT-Connect算法物理对比实验

控制机器人完成真实环境下的导航功能。在图13 所示的真实环境中分别对原始RRT-Connect算法、改进RRT-Connect算法进行导航实验。打开Rviz 可视化界面，完成相应显示配置，进行初始位姿估计并指定目标点，基于建好的环境地图对原始RRT-Connect 算法、改进RRT-Connect 算法进行导航实验，运行结果如图13所示。

图13 Rviz环境下移动机器人路径规划算法效果对比Fig. 13 Comparison of diverse algorithms for mobile robot path planning in Rviz environment

由图13可知：原始RRT-connect全局路径规划算法在所设置的实验室场景下，虽然能够规划出一条从起点到目标点的安全无碰撞行驶路径，但是其所规划出的全局路径存在较多的冗余路径节点，使得移动机器人整体行走路径的质量不高，限制了移动机器人的运行效率。改进后的RRTConnect 全局路径规划算法相对于原始算法而言，移动机器人行走路线大为简化，除转弯处以外均能保持规则直线，行走路径质量得到了显著的提升。路径规划实验结果对比如表3所示。由表3可知：在相同环境下，改进RRT-Connect全局路径规划算法相比于原始RRT-Connect 全局路径规划算法，路径长度缩短了7.37%，运行时间缩短了11.59%。可知，改进后的RRT-Connect全局路径规划算法路径短、质量高，表明该改进算法在实际运行过程中的路径规划效果提升较为明显。

表3 路径规划实验结果对比Table 3 Comparison of path planning experiment results

3.2.2 融合导航物理对比实验

为验证融合算法的实际效果，在室内环境下进行单目标点导航实验，以添加动态障碍物的方式验证改进算法的动态规划效果，改进融合算法实验过程图如图14 所示，实验结果对比如表4所示。

表4 动态避障过程中规划算法对比Table 4 Comparison of planning algorithms during dynamic obstacle avoidance

图14 改进融合算法路径规划实验过程图Fig. 14 Improved fusion algorithm path planning experiment process diagram

在该实验场景下，机器人导航目标点为(3.68，-1.50) m，机器人最终停止点为(3.85，-1.78) m，停止点与目标点的距离为0.33 m，最终距离均小于0.4 m，故机器人成功到达目标点误差允许范围。

在导航过程中，除了主要定位误差外，还需要对比DWA算法和融合算法的路径长度和导航时间，如表4所示。由表4可知：本文融合算法相比于原始DWA算法，最终的路径长度基本相同，但是运行时间缩短了22.56%。因此，改进融合的算法拥有较好的局部规划能力，且效果稳定。

4 结论

1) 为了获取符合室内结构化场景运行需求的移动机器人全局路径与局部路径，提出了一种基于改进RRT-Connect算法的全局路径规划算法和一种基于改进DWA算法的局部路径规划算法。提出的基于人工势场法和范围限定条件的RRT-Connect算法，与原算法相比运行时间最高缩短了92.88%，算法的收敛速度明显加快；提出的基于Dijkstra 算法的节点筛选机制，使最终的全局路径避免了折线和转角过多的问题，与原算法相比路径长度最高缩短了27.3%，路径简化效果明显；提出的融合算法能有效避开动态障碍物且速度波动相对平顺。

2) 为验证所提融合算法的有效性，基于Turtlebot2移动机器人开展了实验测试。改进RRTConnect 算法相比于原始算法，路径长度缩短了7.37%，运行时间缩短了11.59%，效果提升较为明显；改进融合算法相比DWA算法，最终的路径长度基本相同，运行时间缩短了22.56%，效果提升较为明显。

3) 本文所提出的算法目前主要用于室内较为复杂环境下的实现快速路径规划，下一步将尝试针对室外复杂环境以及三维导航下的情况进行改进，从而提高算法的泛化性，以便更好地满足工程实践的需要。