色噪声激励下含分数阶时滞项的广义Van der Pol系统的随机分岔
王 媛, 王慧男, 盛正大, 王 芳
(兰州交通大学 数理学院, 甘肃 兰州 730070)
0 引言
对相对复杂的非线性系统建模时, 用分数阶微积分方程建模比整数阶模型更加简洁准确[1-3], 可以很好地表达时间记忆效果, 精确描述物理力学问题, 因此分数阶系统具有较高的研究价值. 目前分数阶系统已被广泛应用于固体力学、黏性流体力学、信号处理、生物工程学、控制理论等领域[4-6].
近些年关于分数阶系统的动力学行为研究已经取得了一定的进展. Guo等[7]研究了广义Van der Pol系统在白噪声激励下的随机分岔行为; Mathiyalagan等[8]利用Gronwall和随机分析的方法, 研究了分数阶系统在噪声作用下的有限时间稳定性; 唐建花等[9]采用平均法研究了含分数阶导数阻尼项的Van der Pol-Duffing振子的隔振效果, 并讨论了不同参数对力传递率的影响. 但由于系统的复杂性, 许多控制系统的当前状态都不可避免地受到过去状态的影响, 即系统存在一种名为时滞的特性. 它的存在一方面可以让系统的动态性能变差; 另一方面利用时滞设计系统可以改善其控制效果, 很多学者将时滞反馈项引入系统中进行研究: 邱伟达等[10]研究了在Lévy噪声激励下含有时滞反馈的FHN神经元系统的动力学行为, 发现时滞以及噪声偏斜参数均能引起神经元系统状态发生转变; 尚慧琳等[11]研究了引入时滞位置反馈后微陀螺系统的振动跳跃现象等复杂动力学行为; 段绪星等[12]研究了在加性白噪声的激励下, 时滞反馈对三稳态Van der Pol系统稳态响应的影响. 可见引入时滞确实会对系统造成一定的影响, 而目前将时滞反馈项引入分数阶系统的研究还不多, 且选取的噪声以白噪声为主, 对于其他噪声激励下系统的研究还比较欠缺. 因此本文研究了色噪声激励下含分数阶时滞项的广义Van der Pol系统的随机分岔行为, 并运用随机平均法分析了系统的分数阶导数及时滞等参数的改变对系统随机P-分岔的影响.
1 含分数阶导数项的广义Van der Pol系统
考虑在色噪声激励下含分数阶导数项的广义Van der Pol系统:

(1)
其中ε为线性阻尼系数,β1,β2,β3,β4,μ为非线性阻尼系数,w为系统的自然角频率,b1,b2为常数,N(t)为色噪声, 其均值和相关函数满足(2)式, 其功率谱密度为(3)式
(2)
(3)

在Caputo导数意义下, 方程(1)中x(t-τ)的p阶导数定义[13]如下所示:
(4)
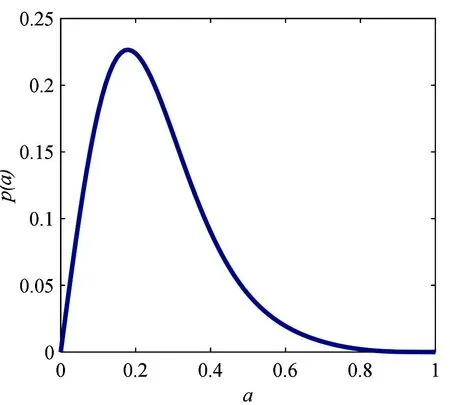
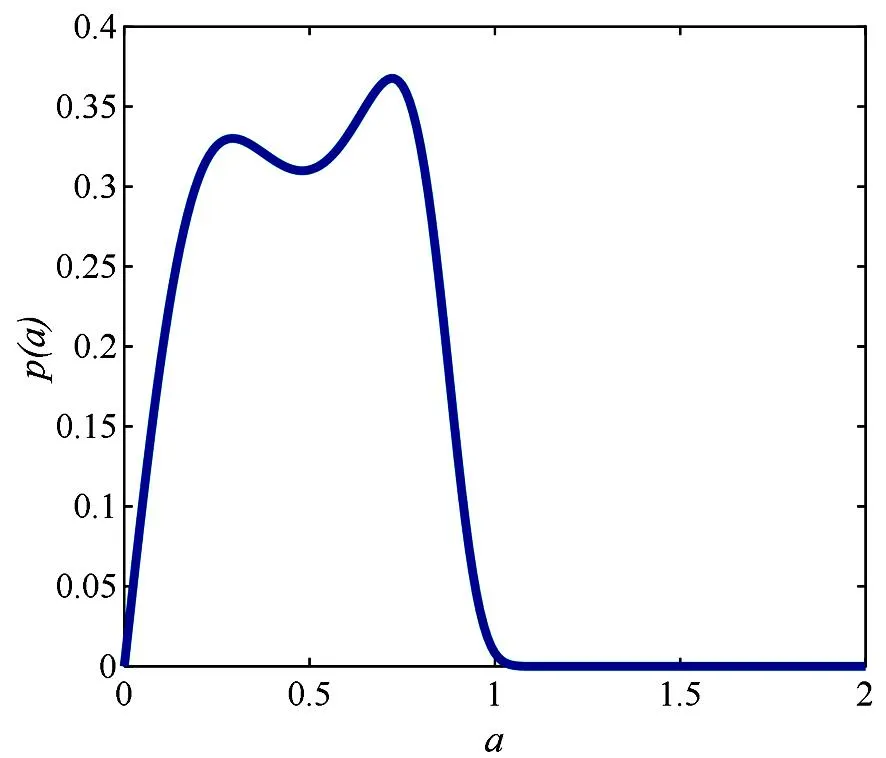
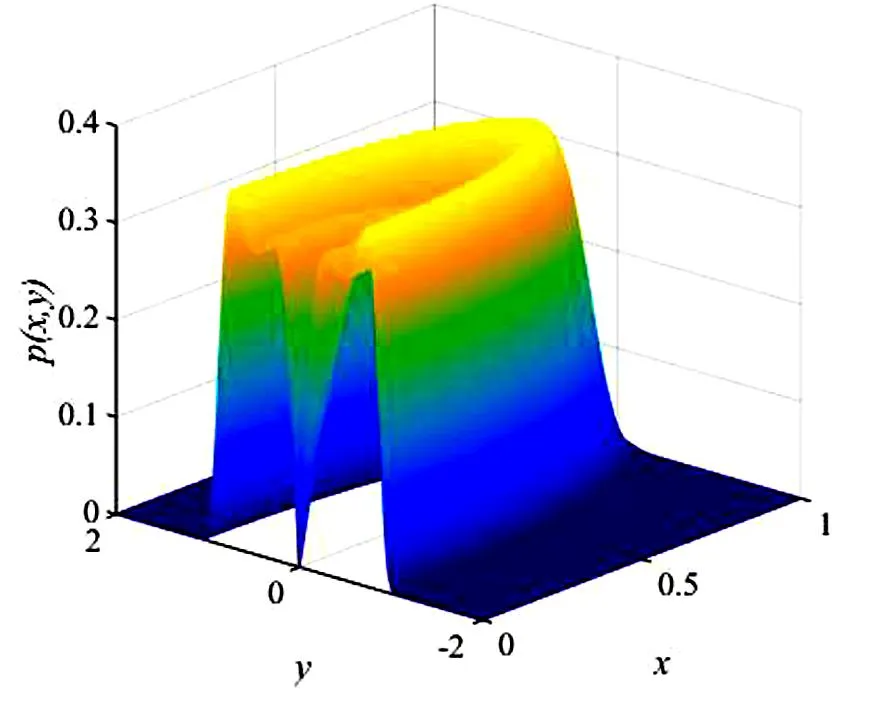
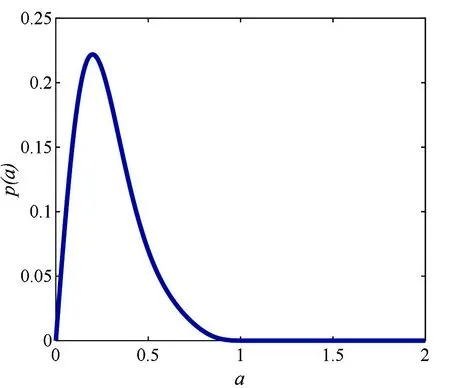
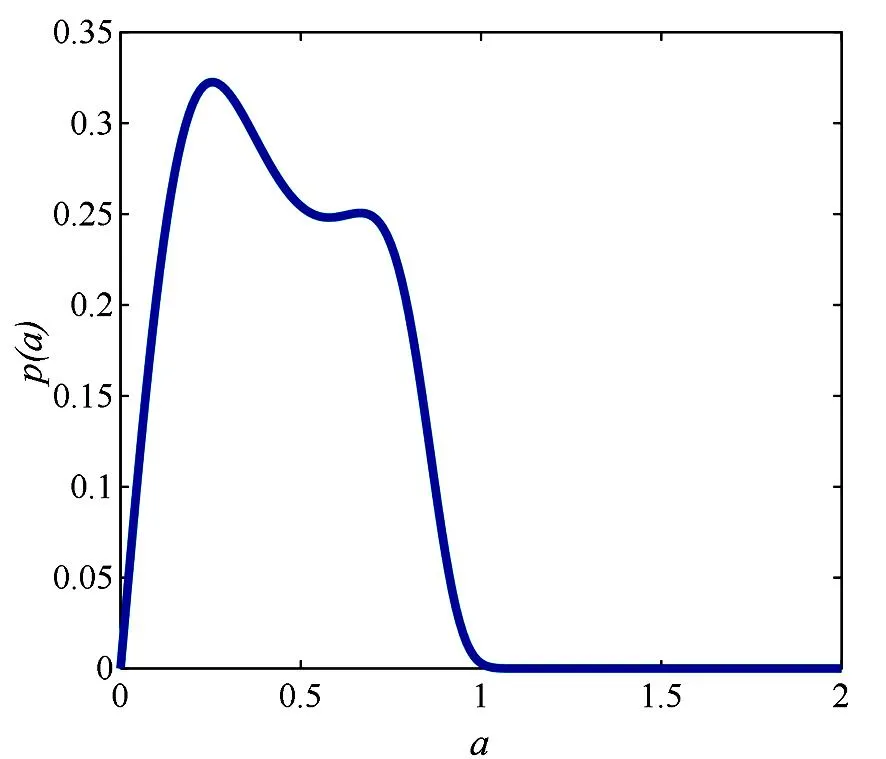
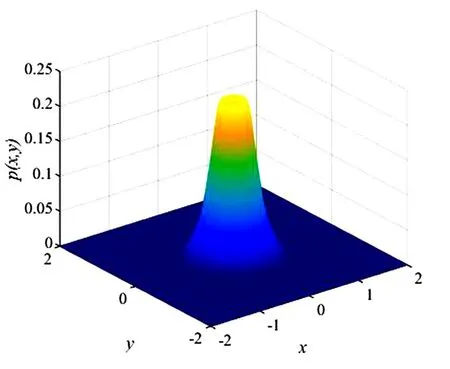
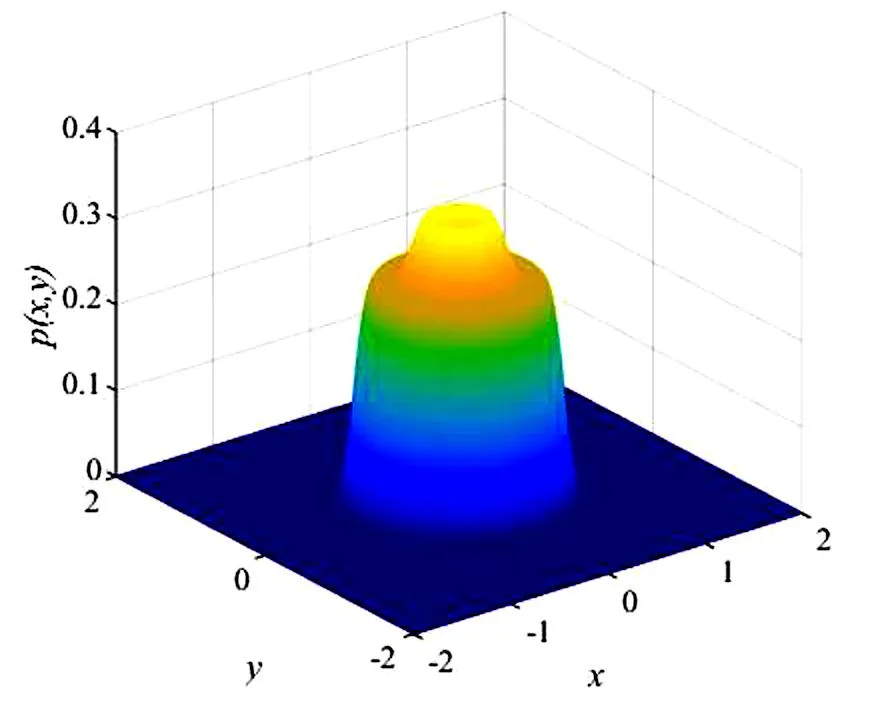
这里n-1 为方便计算, 由文献[14-15]可知, 将分数阶导数项转换为一种回复力和阻尼力的线性组合, 进而得到以下的等效系统 (5) 其中β(p)是等效阻尼力的系数,α(p)是等效回复力的系数. 系统(1)和系统(5)的误差为 (6) 由最小均方误差原则[16-17]可知 (7) 将(6)式代入(7)式中计算可得 (8) 将(1)式的解设为以下形式: (9) 将(9)式代入(8)式并对φ积分平均, 经化简可得 (10) 将(10)式代入(5)式中, 将系统转换成如下形式: (11) 其中 (12) 引入如下变换[18]: (13) 其中a(t),θ(t)分别为系统的幅值过程和相位过程. 根据广义Van der Pol变换, 将(13)式代入(11)式, 由确定性平均法可得以下随机微分方程 (14) 其中 (15) (16) 其中B1(t),B2(t)是标准的维纳过程, 且 (17) 运用随机平均法[19], 将(14)式转化为如下的平均It随机微分方程 (18) 其中的漂移系数和扩散系数分别为 (19) 由(18)式及(19)式可知, 方程中a(t)的表达式与θ(t)是相互独立的, 可得系统对应幅值的FPK方程如下 (20) (21) 其中C为归一化常数, 且满足 这一节主要分析参数的变化对系统发生随机P-分岔的影响, 并通过观察系统的稳态PDF曲线图的峰值个数来判断系统是否发生了随机P-分岔现象. 当b1=1,b2=0时, 系统受加性噪声的影响, 将(19)式代入(21)式,得 (22) 为了方便表示, 可将p(a)设为如下形式 p(a)=CR(a,D,ε,w,p,τ,β1,β2,β3) exp[Q(a,D,ε,w,p,τ,β1,β2,β3)], (23) (24) 固定参数[20]β1=1.45,β2=2.81,β3=-1.68,w=1,τ0=0.3,ε=0.2, 给定参数τ=0.5,μ=0.5,D=0.003, 通过对相关参数p取不同的值, 根据式(22)获得不同形状的稳态概率密度函数曲线图(见图1)以及联合概率密度函数截面图(见图2). (a) p=0.70 (b) p=0.16 (a) p=0.70 (b) p=0.16 由图1及图2可知, 在改变参数p之后, 系统发生了分岔行为. 当p=0.70时, 系统的概率密度函数曲线在离原点不远处有一个较明显的峰; 随着参数p的减小, 概率密度函数曲线在离原点更近的地方出现两个明显的峰, 即系统发生了由单峰到双峰分布的跃迁. 结合图2(a)和(b)所对应的联合PDF曲线的局部截面, 发现系统发生了由单峰分布到双峰分布的跃迁. 由此得出结论, 分数阶导数阶数p的变化会导致系统产生随机P-分岔行为. 选取参数p=0.15,μ=0.5,D=0.008, 通过对相关参数τ取不同的值, 根据式(22)获得不同形状的稳态概率密度函数曲线图(见图3)以及联合概率密度函数截面图(见图4). 由图3及图4可知, 在改变参数时滞τ之后, 系统同样发生了分岔行为. 当τ=0.32时, 系统的概率密度函数曲线在离原点不远处有一个较明显的峰, 随着参数τ的增大, 概率密度函数曲线在离原点更近的地方先后出现一低一高两个明显的峰, 即系统发生了由单峰到双峰分布的跃迁; 结合图4(a)和(b)可知,相应的联合PDF曲线的局部截面图的峰由一个变成了两个. 由此说明时滞τ的引入可以诱导系统发生随机P-分岔. (a) τ=0.32 (b) τ=0.47 (a) τ=0.32 (b) τ=0.47 最后给定参数p=0.15,τ=0.5,D=0.007, 改变分数阶导数的系数μ, 根据式(22)获得不同形状的稳态概率密度函数曲线图(见图5)以及联合概率密度函数截面图(见图6). 由图5及图6可知, 在改变参数μ之后, 系统同样发生了分岔行为. 当μ=0.2时,系统的概率密度函数曲线在离原点很近的地方有一个较明显的峰, 当μ=0.42时, 概率密度函数曲线开始先后出现一高一低两个峰, 即随着参数μ的增大, 系统发生了由单峰到双峰分布的跃迁;结合图6相应的联合PDF曲线立体图,发现系统出现了单峰分布和双峰分布. 由此说明分数阶导数的系数μ的变化可以导致系统发生随机P-分岔的行为. (a) μ=0.2 (b) μ=0.42 (a) μ=0.2 (b) μ=0.42 本文主要研究了在广义Van der Pol系统的分数阶项引入时滞反馈和非线性阻尼项后, 在色噪声激励下的随机分岔问题. 首先将其中的分数阶导数项转换为一种回复力和阻尼力的线性组合, 将分数阶系统变换为整数阶系统之后, 用随机平均法求得伊藤随机微分方程和稳态概率密度函数. 用Matlab绘图验证了分数阶导数阶数p以及时滞τ等参数的改变能引起系统的平稳PDF曲线发生单峰到双峰的跃迁, 即系统产生了随机P-分岔行为. 利用上述特性, 可以对广义的Van der Pol系统进行深入研究, 以减少随机因素对系统造成的影响.
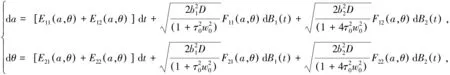

2 系统的随机P-分岔分析

2.1 参数p对系统发生随机P-分岔的影响

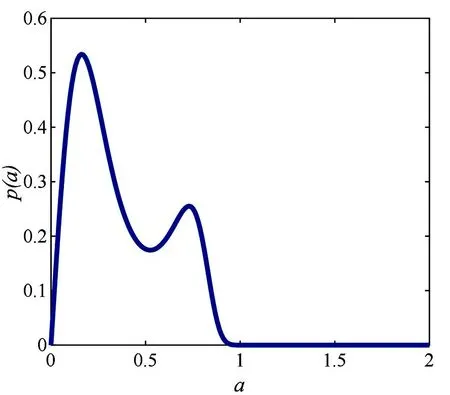
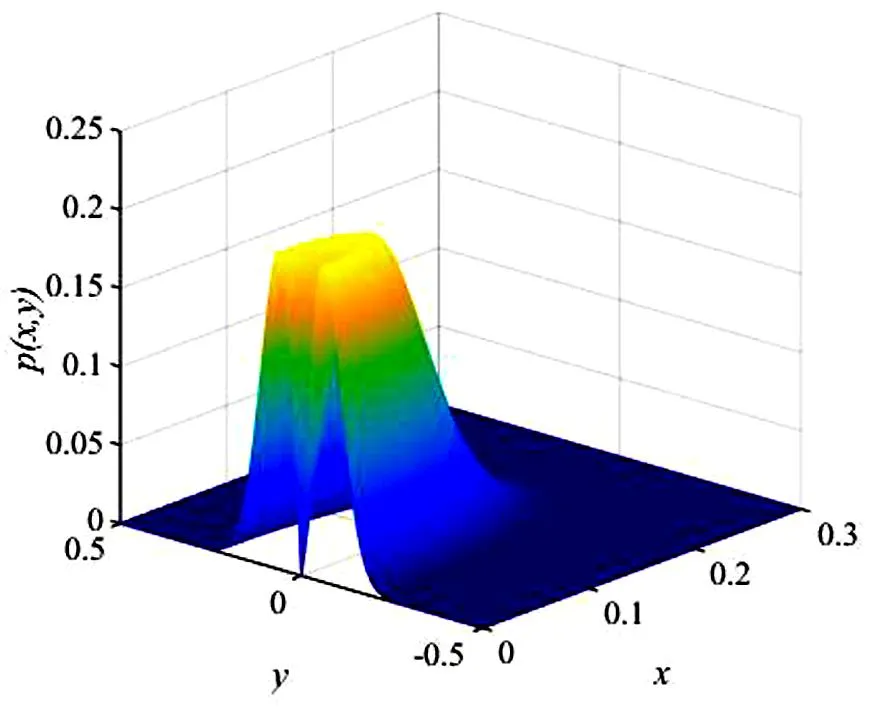
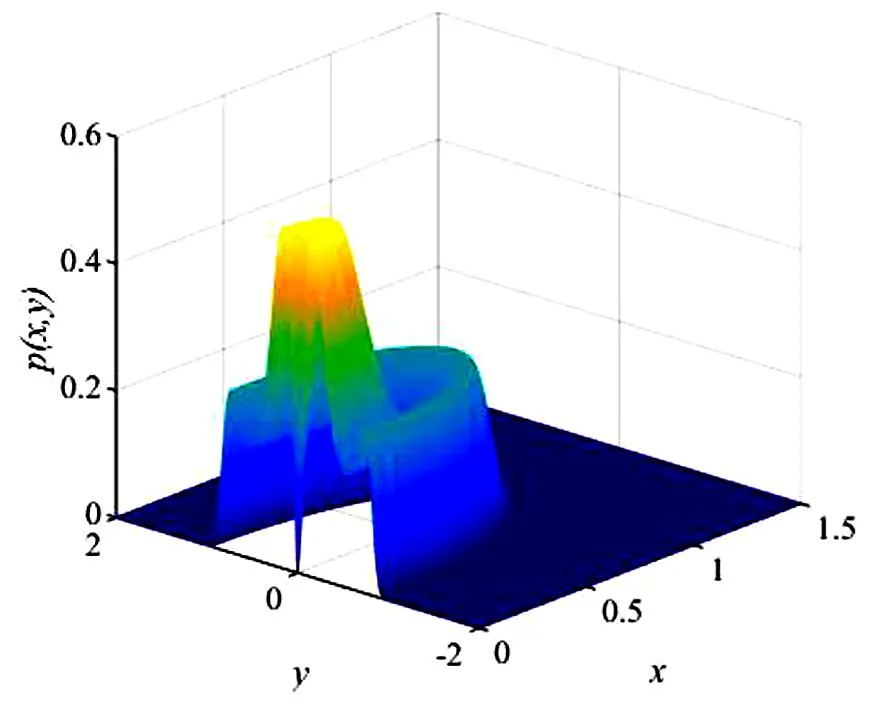
2.2 参数τ对系统发生随机P-分岔的影响

2.3 参数μ对系统发生随机P-分岔的影响
3 结论

