一道2023 年浙江联赛试题的求解与思考

山东省宁阳县复圣中学(271400)张志刚

1 试题呈现

题目(2023 年全国高中数学联赛浙江赛区预赛第13 题)已知椭圆的上顶点A与左顶点B的距离为,离心率为,P(t,0)(-4 ≤t≤-1)为x轴上一点.

(1)求椭圆方程;

(2)连接AP交椭圆于点C,过点C作x轴的垂线,交椭圆另一个点D,求S∆ABD的取值范围.

本题探求解析几何经典问题之一的“三角形面积的取值范围”,引导学生学会灵活应用解析几何的基本思想方法对问题进行合理转化,达到通过增加思维量来选拔创新拔尖人才的目的,同时对培养学生核心素养、引导中学数学教学具有积极的导向作用.

2 试题解答

2.1 解题思路

解析几何的研究对象是几何图形, 以平面直角坐标系为研究工具, 通过代数运算研究几何问题.这是解析几何的特征[1].坐标法的要点是通过代数运算和推理研究几何图形, 同时这里的运算带有几何直观.第(1) 问, 由题设条件,结合离心率性质,可轻松确定椭圆的方程, 通过本小问“铺路搭桥”, 让考生有获得感.第(2) 问探求∆ABD面积的取值范围,关键步骤是: 一是选取适当的参数作为自变量表示∆ABD的面积, 建立目标函数; 二是求出该目标函数的值域.如何选择恰当的函数,对考生分析问题、解决问题的考查增加了难度,提升了思维强度,要求考生结合点A,P,C,D坐标的关系及椭圆的方程,从直接表征或间接刻画等视角构建目标函数.若选取题设参数t作为自变量, 通过运算将∆ABD的面积表示为函数, 经换元m= 5-t后, 进一步转化为,借助对钩函数的单调性即可求出函数的值域, 具体见解法1-5.也可另辟蹊径, 选取某直线(如OD)的斜率为k作为自变量, 将∆ABD的面积表示为k的函数,同样可由对钩函数的单调性求出值域,见解法6.解答中应充分利用椭圆的几何性质及平面几何中的定理、性质等辅助求解,如解法2.

2.2 解题过程

思路一(直接法)考虑利用建立目标函数,其中d是点D到直线AB的距离,如图1 示.

图1

解法2(特殊位置分析)本题中,点D的位置受制于点P.下面借助几何直观,考查点P运动时d的变化规律,由临界位置确定d的极值,进而求得面积的取值范围.

由解法1 知, 点D的坐标是,.

如图2,当t=-1 即点P位于P1(-1,0)时,点D的坐标是.

图2

当t= -4 即点P位于P2(-4,0) 时, 点D的坐标是.

当平行于AB的直线与椭圆切于第二象限内的点D(x0,y0) 时,d取得最大值,S∆ABD最大.设此切线为: 4x- 5y+m= 0(m>0), 将其与椭圆方程联立得32x2+ 8mx+m2- 400 = 0, 由∆= 0 得,此时的解是, 即.此时,.

综上,S∆ABD的取值范围是.

思路二(间接法)通过作辅助线, 借助∆ABD与其他三角形之间的联系表示其面积,体现分解与综合、化难为易的转化思想.

解法3(作差法表示面积)如图3,延长AD交x轴于点E,由解法1 知,点D的坐标是,所以直线AD的方程是.令y= 0,解得,故点E的坐标是,故

图3

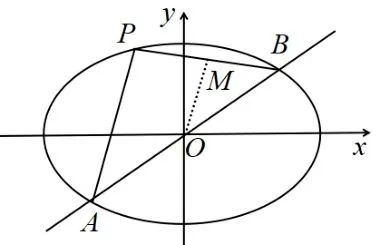
图4

图5

下同解法1.

解法4(间接法——解法3 优化)

评注解法4 利用椭圆的性质,规避了解法3 中求解点D的坐标的繁琐运算,确定直线AD的方程更便捷.

解法5(面积拆分与重组)如图6,

图6

下同解法1.

以上解法均是选用题设中的参数作为自变量,建立了面积的目标函数,进而求出取值范围.然而,选取直线的斜率作为自变量建立函数关系,是解析几何范围(最值)问题更常见的操作.下面尝试选取某条直线,以其斜率k建立三角形面积的函数.

解法6(变换变量) 如图5, 延长DO, 交椭圆于点E,设直线OD的斜率为k(k<0),则直线OD的方程为:y=kx(k<0),将其与椭圆方程联立得(16+25k2)x2-400 =0, 解得(舍) 或, 故点D的坐标是,

3 思维障碍与突破

以上解答各有千秋, 建立的三角形面积的目标函数也不尽相同, 如或.但在后续求解函数的值域时, 不少考生表现出手足无措,解答结果不尽如人意.究其原因,主要是当前各版本教材都未对分式函数值域进行系统阐述,学生缺乏成熟的求解策略.事实上, 分式多项式函数有“齐次”(如)和“非齐次”(如)两类,处理路径如下:

途径1(齐次式: 分子常数化) 若, 可借助“添项、拆项、系数拼凑”等技巧, 通过恒等变形把分子化为常数, 即将函数变形为,然后结合反比例函数的单调性及图象变换知识确定值域.例如, 求的值域.由于, 结合f(x) 的图象知,f(x)在[1,2]上单调递增,所以.对于“”型可进行类似处理.

途径2(非齐次式:1 次式换元)若时,可令t=ax+b,则函数转化为,然后分子分母同时除以t, 再利用函数的单调性或基本不等式讨论其值域.若, 可进行类似换元处理.例如, 求的值域.令t= 2x+1,t≥3, 则,因为函数在[3,+∞)上单调递增,所以f(x)∈[3,+∞).

下面再举两例说明.

例1(2014 年高考全国新课标I 卷理科第20 题)已知点A(0,-2),椭圆的离心率为,F是椭圆的右焦点,直线AF的斜率为,O为坐标原点.

(Ⅰ)求E的方程;

(Ⅱ)设过点A的直线l与E相交于P,Q两点,当∆OPQ的面积最大时,求l的方程.

评注本题中的目标函数本质上是“”型分式函数, 经换元转化为,再借助基本不等式求出值域.

由于四边形的面积可分解为三角形面积之和,故上述策略也适用于四边形面积的取值范围.

例2(2016 年高考全国新课标I 卷理科第20 题)设圆x2+y2+2x-15=0 的圆心为A,直线l过点B(1,0)且与x轴不重合,l交圆A于C,D两点,过B作AC的平行线交AD于点E.

(I)证明|EA|+|EB|为定值,并写出点E的轨迹方程;

(II)设点E的轨迹为曲线C1,直线l交C1于M,N两点,过B且与l垂直的直线与圆A交于P,Q两点,求四边形MPNQ面积的取值范围.

解(I),过程从略.

(II)因为直线l与x轴不重合,故设l:x=my+1,过B且与l垂直的直线PQ的方程为:y=-m(x-1).将l与椭圆方程联立得(3m2+4)y2+6my-9=0.设M(x1,y1),N(x2,y2), 则.又

故四边形MPNQ的面积

因为m2≥0,所以,故即四边形MPNQ面积的取值范围为.

评注以上计算得四边形MPNQ面积中, 此时根号内为“”型齐次式, 为此进行分子常数化处理得,进而求得值域.

4 结束语

解析几何是数形结合的学科,“通过几何建立直观,通过代数予以表达”是其基本理念[2].解析几何中的运算是建立在几何背景下的代数运算,所以先用几何眼光观察,分析几何图形的要素及其基本关系,再用代数语言表达,而且要注意利用图形的几何特征及图形间的关系简化运算.例如,前文对三角形面积取值范围的研究中,直观认识各几何要素间的位置分析是第一步.教师要以典型例题为载体,引导学生利用已有知识和学习经验,深刻理解运算对象,科学设计运算程序,明晰运算机理,熟练掌握运算法则,准确求得运算结果,有效解决实际问题,如本文探讨的分式函数的值域.