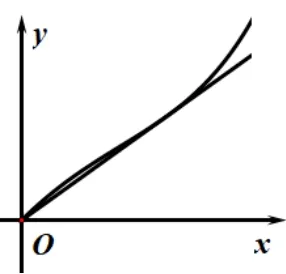“端点效应”失效原因分析及解决方法

江西省九江市第三中学(332000)吴丛新

不等式恒成立求参数取值范围问题是高考的热点,也是难点问题,其通法是构造函数分类讨论,但过程往往十分繁琐,计算量庞大.倘若函数在区间端点满足一定的条件,则可考虑“端点效应”进行必要性探路.然而有时端点效应会出现失效,即其充分性不成立的情况.本文结合实例对端点效应成立的条件及其失效原因进行分析,并提出解决问题的相应方法.

一、“端点效应”基本原理及解题步骤

(1)必要性缩小范围:

①若f(x,m) ≥0 (m为参数) 在[a,b] 上恒成立, 且f(a)=0(或f(b)=0),则f′(a)≥0(或f′(b)≤0).此法适用于区间端点处函数值为零的情况.

②若f(x,m) ≥ 0 (m为参数) 在[a,b] 上恒成立, 且(或), 则f′′(a) ≥0(或f′′(b) ≤0).此法适用于区间端点处函数值为零且导数值也为零的情况.

(2)充分性验证结果:

利用第一步中的参数范围,通过f′(x)判断f(x)的单调性,验证f(x)min≥0.

二、“端点效应”有效应用举例及原因分析

例1已知f(x)=aex+2e-x+(a-2)x(a∈R).

(1)略;(2)当x≥0 时,f(x)≥(a+2)cosx,求a的取值范围.

分析构造函数g(x) =aex+2e-x+(a-2)x-(a+2)cosx,x> 0,注意到g(0) = 0,考虑端点效应,g(x) ≥0 的必要条件是g′(0)≥0.

解析令g(x)=aex+2e-x+(a-2)x-(a+2)cosx,g′(x)=aex-2e-x+(a-2)+(a+2)sinx,g(0)=0,因此要使g(x)≥0 在[0,+∞)上恒成立,则g′(0)=2(a-2)≥0,即a≥2(必要性).

再证充分性.当a≥2 时,

所以g′(x)在[0,+∞)上单调递增,g′(x) ≥g′(0) ≥0,g(x)单调递增,g(x)≥g(0)=0.

评析本题中二阶导数g′′(x) ≥0 保证了g′(x) 在[0,+∞)上单调递增,所以g′(x) ≥0,从而保证原命题成立.因此本题中必要性探路点x= 0 不仅为区间端点,同时也是一阶导数g′(x)的单调区间的端点,所以端点效应不能简单理解为题目所给区间的端点简单代入,否则会出现端点效应失效的情况.

三、“端点效应”失效原因分析及解决方法

例2已知当x≥0 时,ex-x2-(a-1)x-1 ≥0 恒成立,求a的取值范围.

分析令g(x)=ex-x2-(a-1)x-1,注意到g(0)=0,考虑端点效应.g′(x) = ex- 2x- (a- 1), 因此要使g(x) ≥0 在[0,+∞) 上恒成立, 则g′(0) = 2-a≥0, 即a≤2.g′′(x) = ex-2.在[0,ln 2)上,g′′(x) < 0,g′(x)单调递减, 在[ln 2,+∞)上,g′′(x) > 0,g′(x)单调递增.所以g′(x)min=g′(ln 2) = 3-2 ln 2-a,当a≤2 时,g′(x)的正负号不确定,g′(x)不恒为正,故不能保证g(x) ≥0 恒成立,所以端点效应失效.要得到原命题成立的充要条件,需要对g′(x)的正负号进行分类讨论,要确保g(x)的极小值大于0.笔者在端点效应基础上,进一步分析得到如下解答:

对g′(x)min=g′(ln 2) = 3-2 ln 2-a的正负号进行分类讨论:

①当g′(ln 2)≥0,即a≤3-2 ln 2 时,g′(x)≥0,g(x)单增,g(x)≥g(0)=0,符合题意

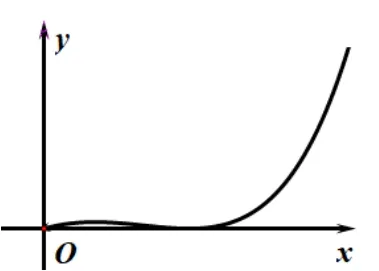
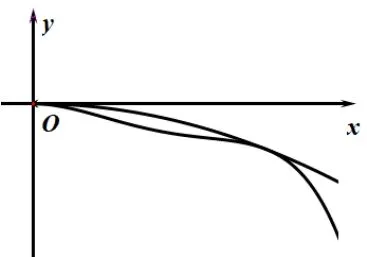
②当g′(0)>0 且g′(ln 2)<0,即3-2 ln 2

因为ex0-x0-1 ≥0,所以ln 2

设φ(x) = ex-2x,x∈(ln 2,1],φ′(x) = ex-2 > 0,φ(x)在(ln 2,1]上单增,所以φ(x)∈(2-2 ln 2,e-2].所以a-1=ex0-2x0∈(2-2 ln 2,e-2].所以a∈(3-2 ln 2,e-1].

③当g′(0) ≤ 0, 即a≥ 2 时,g′(x) 在(0,ln 2) 上单减, 故g′(x)

综上,a∈(-∞,e-1].

据上述解答过程可以发现,为保证g(x)min≥0,需极小值点x0≤1,x0=1 为临界点,代入g(1)=e-1-a≥0 得a≤e-1,可知临界点x0= 1 恰好是不等式g(x) ≥0 的充要条件.为何x0= 1 是g(x) ≥0 的充要条件呢? 实际上当g(x)min= 0 时,x0= 1(如图1),即g(x)在x0处取极小值0.故x0应满足两个条件:

图1

消a得(1-x0)(ex0-x0-1) = 0, 易证当x> 0 时,ex0-x0- 1 > 0, 故满足这两个条件的唯一点x0= 1.不妨称该点为“内点”.以内点作为必要性探路点,得到不等式恒成立的必要条件,再证其充分性即可.

如果对不等式进行等价变形,可得到不同的函数解析式,而“内点”却具有一致性.如下:

考虑参数分离法: 当x> 0 时,, 由得x0= 1 为该函数唯一极小值点.

从函数图像的凹凸性和共切点的角度考虑, 将原不等式变形可得(a- 1)x≤ ex-x2- 1.令h(x) =ex-x2- 1.设y= (a- 1)x与y=h(x) 相切于点(x0,y0)(如图2),则,化简得(1-x0)(ex0-x0-1) = 0.解得x0= 1 为两函数唯一共切点.

图2

下面我们利用上述方法来求解一道高考真题.

例3(2020 年高考全国Ι 卷理科第21 题) 已知f(x)=ex+ax2-x.(1)略;(2)当x≥0 时,,求a的取值范围.

分析令, 注意到, 注意g′(0) = 0;g′′(x) = ex-3x+2a, 因为g′(0) = 0, 考虑端点效应, 则g′′(0) ≥0, 即, 在[0,ln 3) 上,g′′′(x) < 0,g′′(x) 单调递减, 在(ln 3,+∞) 上g′′′(x) > 0,g′′(x)单调递增.

g′′(x)min=g′′(ln 3) = 3-3 ln 3+2a, 当时,g′′(x) 的正负号不确定, 导致g′(x) 不恒为正, 故不能保证g(x) ≥0 恒成立,所以端点效应失效.这时候我们可以寻找“内点”x0.x0应满足两个条件:

消a得,易证当x0>0 时,,故满足这两个条件的唯一点x0=2.

将该点代入g(2) = 4a+e2-7 ≥0,得为不等式恒成立的必要条件.下面证其充分性.

当a≥(7-e2)/4 时,

令h(x) = ex-3x+(7-e2)/2,h′(x) = ex-3 在[0,ln 3)上单调递减,在(ln 3,+∞)上单调递增,故

所以g′′(x) > 0,g′(x) 在[0,+∞) 上单调递增,g′(x) ≥g′(0) = 0, 所以g(x) 在[0,+∞) 上单调递增, 故g(x) ≥g(0)=0.

如果对不等式进行等价变形,可得到不同的函数解析式,而“内点”却具有一致性.如下:

从函数图像的凹凸性和共切点的角度考虑,将原不等式变形(半分离参数).变形方式一:,设y=ax2与图像的共切点为(x0,y0)(如图3),则

图3

图4

消a得,易证,所以x0=2,a=(7-e2)/4.结合函数图像的凹凸性及二次函数开口大小与a的关系可知,当a≥(7-e2)/4时,原不等式恒成立.

此外,从指数找朋友的角度考虑,可将原不等式变形为

所以要证g(x) ≤1,只需证,令

因为g(x)在,(2,+∞)上单调递减,在上单调递增,所以x= 2 为极大值点,所以当a≥(7-e2)/4时,g(x)≤1.

端点效应本质是极限的保号性的一种特殊情况,即临界点恰好为区间端点,若临界点不为区间端点,则所得结果是原命题成立的必要不充分条件.这时,我们可以寻找“内点”.还可对原不等式进行适当变形,可得函数不同的解析式表达,探路点虽含义不同,但却具有一致性,如本文中出现的极值点、共切点等不同名称,它们其实是同一个点.因此,我们在不等式恒成立问题求参数取值范围问题中,应先进行单调性分析,若出现端点效应失效时,可寻找内点,也可对原不等式进行合理变形,进行必要性探路,并验证其充分性,保证所求范围的充要性.