一类无关联双变元问题的解析

福建省福清第三中学(350000)唐洵

1 题目呈现

以双变元问题为压轴的导数试题在高考中屡见不鲜,问题中的两个变元之间往往存在着某些联系,解题时可以此为依据,通过消元或换元来减少变元的数量;但若是双变元之间不存在任何关联,问题又当如何处理?

题目1(2023 年嘉兴二模第22 题)已知函数f(x)=ex,g(x)=lnx.

(1)若存在实数a,使得不等式f(x)-g(x)≥f(a)-g(a)对任意x∈(0,+∞)恒成立,求f(a)·g(a)的值;

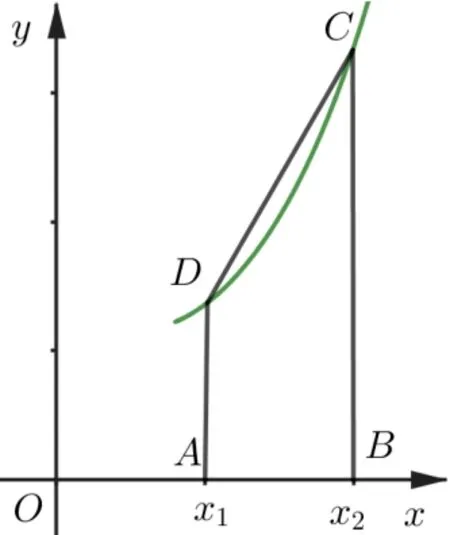
(2) 若1

①存在x0∈(x1,x2),使得成立;

2 解法探究

由于本文的重点在研究第(2)小题的第②问,对于第(1)小题以及第(2)小题的第①问,这里仅给出参考答案,不作说明,有兴趣的读者可以自行探究.

解析(1)令h(x) =f(x)-g(x) = ex-lnx,;令u′(x) =xex-1,则u(x)在(0,+∞)上单调递增,而,u(1)=e-1>0,故存在,使得u(a) =aea-1 = 0,且h(x)在(0,a)上单调递减,在(a,+∞)上单调递增,所以h(x)≥h(a)对任意x∈(0,+∞)恒成立;此时;

当x∈(1,+∞)时,则, 故h′(x)在(1,+∞)上单调递增且下凸,作出y=h′(x)的大致图像如图1 所示,∫表示曲边梯形ABCD的面积,表示梯形ABCD的面积,故由图可知,故(∗)式成立,即.

图1

3 试题背景

(1)凹凸性定义设函数y=f(x) 在区间I上连续:若∀x1,x2∈I, 恒有, 则称y=f(x)的图像是凹(下凸)的,函数y=f(x)为凹(下凸)函数;若∀x1,x2∈I,恒有,则称y=f(x)的图像是凸(上凸)的,函数y=f(x)为凸(上凸)函数;

(2)凹凸性判定设y=f(x)在[a,b]上连续,且在(a,b)内具有一阶和二阶导数; 若f(x) 在(a,b) 内有f′′(x) > 0,则f(x) 在[a,b] 上是凹(下凸) 函数, 若f(x) 在(a,b) 内有f′′(x)<0,则f(x)在[a,b]上是凸(上凸)函数;

(3)哈达玛(Hadamard)积分不等式设函数f(x)是区间[a,b] 上的凹(下凸) 函数, 其中a≤x1

注哈达玛(Hadamard)积分不等式的证明文[1]中已经给出,这里不再赘述.

(4)对数平均不等式若a>0,b>0,且ab,则

其中a,b∈R,且ab;事实上①②两个不等式是哈达玛积分不等式的特殊形态.

4 命题步骤

根据上述背景,本题第(2)题第②小题命题步骤如下:

第一步, 确定母函数: 选取一个函数F(x), 确定区间[a,b],使得F(x)在[a,b]上是凹(下凸)函数,题1 选择的函数为,x∈(1,+∞);

第二步,代入不等式: 利用哈达玛积分不等式得到一个相关的不等式链,题目1 中的不等式链为

第三步,选择证明点: 在上述不等式中,选择合适的部分作为证明的主体(左右两侧不等式均可,常见的为右侧的证明),即

第四步,均值来变形: 为了加大难度,先利用基本不等式进行放缩,得到

再整理得到

再注意到(ex)′= ex,于是令f(x) = ex,g(x) = lnx,便得到题目1 的主干部分.

对该问题进行简单推广可以得到: 若a> 1, 函数f(x) =ax,g(x) = logax,h(x) =f(x) -g(x), 则当1

5 类题赏析

题目2 (2023 年潍坊三月测评第22 题) 已知函数f(x)=ex+kln(x+1)-1(k∈R).

(1)当k= 1 时,求曲线y=f(x)在点(0,f(0))处的切线方程;

(2)对任意x∈(-1,+∞),都有f(x)≥0,求实数k 的取值范围;

题目3(2020 年高考天津卷第22 题) 已知函数f(x)=x3+klnx(k∈R),f′(x)为f(x)的导函数.

(1)当k=6 时,

①求曲线y=f(x)在点(1,f(1))处的切线方程;

(2)当k≥-3 时,求证: 对任意的x1,x2∈[1,+∞),且x1>x2,有.

题目4(2013 年高考陕西卷理科第21 题) 已知函数f(x)=ex,x∈R.

(1)若直线y=kx+1 与y=f(x)的反函数的图像相切,求实数k的值;

(2)设x> 0,讨论曲线y=f(x)与曲线y=mx2(m>0)公共点的个数;

(3)设a

简析题目2(3): 当时,在(0,+∞) 上恒成立, 故f′(x) 在[0,+∞)为凹(下凸)函数,不妨设s

题目3(2): 当k≥-3 时,在(1,+∞)上恒成立,故f′(x)在[1,+∞)为凹(下凸)函数,根据哈达玛积分不等式,

题目4(3): 易知f(x) = ex为凹(下凸) 函数, 且f′(x)=f(x),根据哈达玛积分不等式,