基于LIEF的喷雾数值仿真模型验证

李岩松,崔明利,李雪松,许敏

(上海交通大学智能汽车研究所,上海 200240)

在汽油直喷(GDI)发动机中,空气与燃料形成的混合气特性直接影响混合气燃烧过程,进而影响发动机的动力性、经济性和排放特性,对发动机燃烧性能起到决定性作用。在发动机燃烧系统的开发中,腔内混合气的优化主要依赖于油气匹配和燃烧策略,喷雾数值仿真是辅助制定该策略的关键环节。许多研究证实了燃料的蒸气会影响缸内均匀性,从而影响发动机的燃烧性能。通常应用商用计算流体动力学(CFD)软件作为主要模拟手段。

目前的喷雾数值仿真研究一般通过应用各类子模型和经验假设模拟喷雾发展过程,获取喷雾的贯穿距、落点分布、粒径特征等。Ho Teng[1]采用经验分布模型分析了液滴粒径的空间分布,预测了喷射压力分别为4,10,15 MPa时的燃料贯穿距、喷雾锥角和液滴大小,并研究了燃油瞬态蒸发速率,为确定空气与燃料混合的最优喷射时机提供了有用参考。Z. F. ZHOU等[2]基于液滴内部温度遵循三阶多项式分布的假设,提出了一种新的液相模型,但该模型只能预测初始加热期间内部温度的单调变化,并不能每次都吻合试验数据。 Chungen Yin等[3]将液滴沿径向、极向和方位角方向离散成若干个控制体积,利用有限体积法对每个控制体积上的流动、传热和传质进行数值求解,建立了充分考虑液滴内部循环、传热和传质的模型,但是没有对其正确性进行试验验证。此外,液滴间的相互作用对混合也有影响,特别是在喷雾模型上,它会使燃料的液相和气相分布发生显著变化。根据O’Rourke的研究[4],稠密喷雾中的液滴碰撞聚合作用最多使液滴平均尺寸增加7倍,使液滴阻力与蒸发率显著偏离预估值。

本研究基于Converge软件的O’Rourke湍流扩散模型与Frossling蒸发模型建立了喷雾蒸发模型,对喷雾的蒸发过程进行了数值模拟,并采用复合激光诱导荧光 (LIEF) 技术在定容弹中测定了喷雾的液相与气相的空间分布,对仿真结果进行了验证。根据验证结果对仿真模型进行了分析,发现了所采用液滴破碎模型的不足之处,为未来进一步提高该模型的精度提出了针对性的建议。

1 喷雾蒸发模型仿真

1.1 物理模型参数设置

本次仿真采用的喷雾蒸发模型使用商业计算流体动力学软件Converge建立。喷雾所在的容器设为定容弹,其物理模型设置为直径200 mm、高度200 mm的圆柱体,与后期试验验证使用的定容弹参数保持一致。容器内部温度设为(298±1) K,压力设为100 kPa。喷油器模型设置为单孔喷油器,喷嘴直径为0.2 mm,长径比为2.5。将长径比设为2.5有利于获得较大的喷孔流量系数,减少燃料所受到的压力损失,从而使得喷雾获得较强的贯穿能力,形成贴近真实场景的小锥角燃料束。喷射压力设为10 MPa,喷油持续时间设为1 ms,喷嘴与竖直方向夹角设为30°。

在试验验证环节中,使用双相激光诱导荧光技术对喷雾进行形态与参数的测量。为了使荧光能够更好地反映喷雾的蒸发过程,示踪粒子和基础燃料必须具有良好的共蒸发特性。由于汽油为混合物,含有多种在激光激发时能够产生各种波长荧光的物质,因此汽油不适宜作为测试燃料的基础燃料。根据Fansler[5]和H. S. Guo等[6]的研究,基础燃料正已烷(n-hexane)、氟苯(Fluorobenzene,FB)和2,6-二乙基-4-甲基苯胺(Diethyl-Methyl-Amine,DE-MA)是一种较好的组合,具有良好的共蒸发特性,气液两相的荧光光谱重叠区域小。

根据H. S. Guo等[6]的研究,正己烷、DEMA和氟苯在体积比为89∶9∶2时具有较好的温度敏感性,且能够保证其荧光强度,因此,本研究中选择该配比燃料进行测试研究。测试燃料的物理和热特性采用Convergence中CHEMKIN文件的标准数值。仿真物理模型初始条件如表1所示。

表1 喷雾蒸发模型初始条件

1.2 仿真模型设置

仿真模型的网格划分使用了AMR自适应网格方法。该方法最早是由Berger 和Oliger于1984年提出的,是通过求解椭圆型方程的边值问题来数值生成网格的一种新方法。它是在任意形状的区域上求偏微分方程的数值解的一种非常有效的工具。该方法抛弃了等距均匀的差分网格,采用能够自动地适应所研究问题中解的特征疏密程度不均的曲线网格,如在边界上计算网格与实际边界相重合,在区域内部可任意调节网格点的疏密程度等。图1示出了基于AMR方法的网格划分。经过网格无关性检验之后,设置喷雾的核心分布区域网格大小为0.5 mm,其余区域为2 mm。此处AMR方法的生效对象设置为流场的速度梯度,生效条件为1 m/s,最大单位网格数为1 200 000。同时,针对喷油器喷嘴附近进行固定嵌入式网格设置,放大倍数为2,以保证喷嘴边缘的喷雾仿真结果更加细致。仿真模型的网格设置见表2。

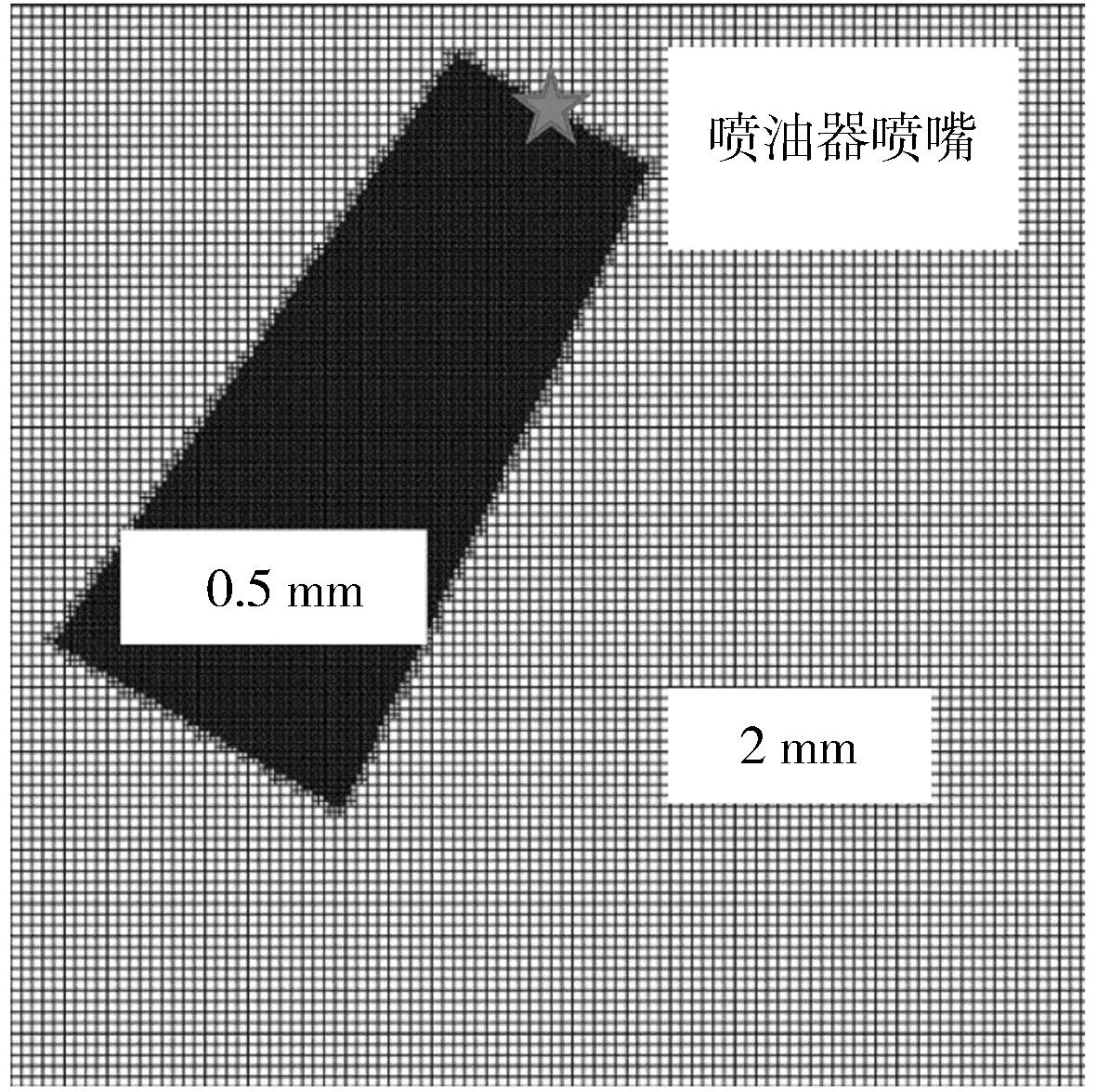
图1 喷雾仿真网格布局示意

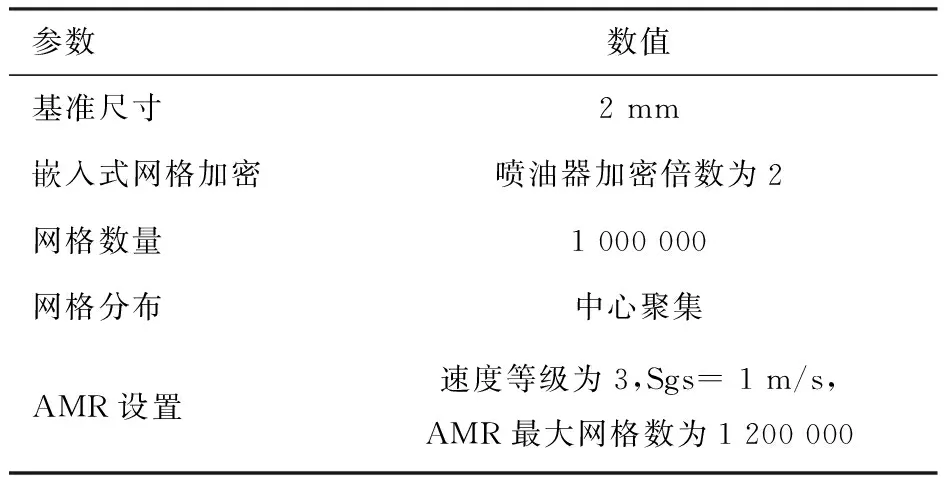
表2 仿真模型网格设置

由于在喷雾的核心区域液滴之间会发生极其剧烈的碰撞效应,而该效应会对液滴的速度与尺寸分布都产生较大影响,因此在仿真中需要采用对应的液滴碰撞模型。本次仿真采用主流的O’Rourke模型来控制喷雾产生过程中的湍流扩散。该模型使用由O’Rourke提出的蒙特卡罗方法来计算液滴碰撞,这是一种基于Brazier Smith的水滴碰撞试验结果[7]的标准计算方法,假设只有当液滴处于相同的气相单元时才能发生碰撞。由于该模型只考虑聚合和摩擦分离两种可能,因此大大简化了碰撞结果。蒸发模型采用同样主流的Frossling模型。另外在仿真中使用了考虑液滴破碎情况的动态液滴阻力模型与NTC碰撞模型。

为了控制索特平均直径的范围以及试验目标的喷雾贯穿过程,需要在仿真中引入液滴破碎模型。本次仿真选用的液滴破碎模型为修正KH-RT模型,由KH模型控制初次破碎,并在此过程中产生子液滴;后续液滴破碎则由KH与RT模型竞争机制决定。KH-RT混合模型同时考虑KH与RT两种模型的机制,既考虑气液流体相对运动以及黏性力作用,又考虑基于离散液滴的分裂雾化。其中,在气液界面的法向会存在由于两相之间密度的巨大差别而生成的惯性力,继而引起扰动波。 KH-RT喷雾破碎模型的后续雾化效果优于其他几种模型,这是由于KH-RT 喷雾破碎模型喷雾贯穿距高,雾化效果更好[8]。

由图2可知,KH-RT喷雾破碎模型假定液滴气泡初始直径与喷油器喷嘴大小相同,在特征破碎距离之内,液滴破碎过程以KH模型为主,而在特征破碎距离之外则是KH与RT双模型协调作用。本研究选择的修正KH-RT模型就是将液滴破碎细分为初次破碎和二次破碎,由KH模型控制液滴的初次破碎,并在此过程中产生子液滴,子液滴的再次破碎被形容为二次破碎,二次破碎则由KH与RT 模型竞争机制决定。

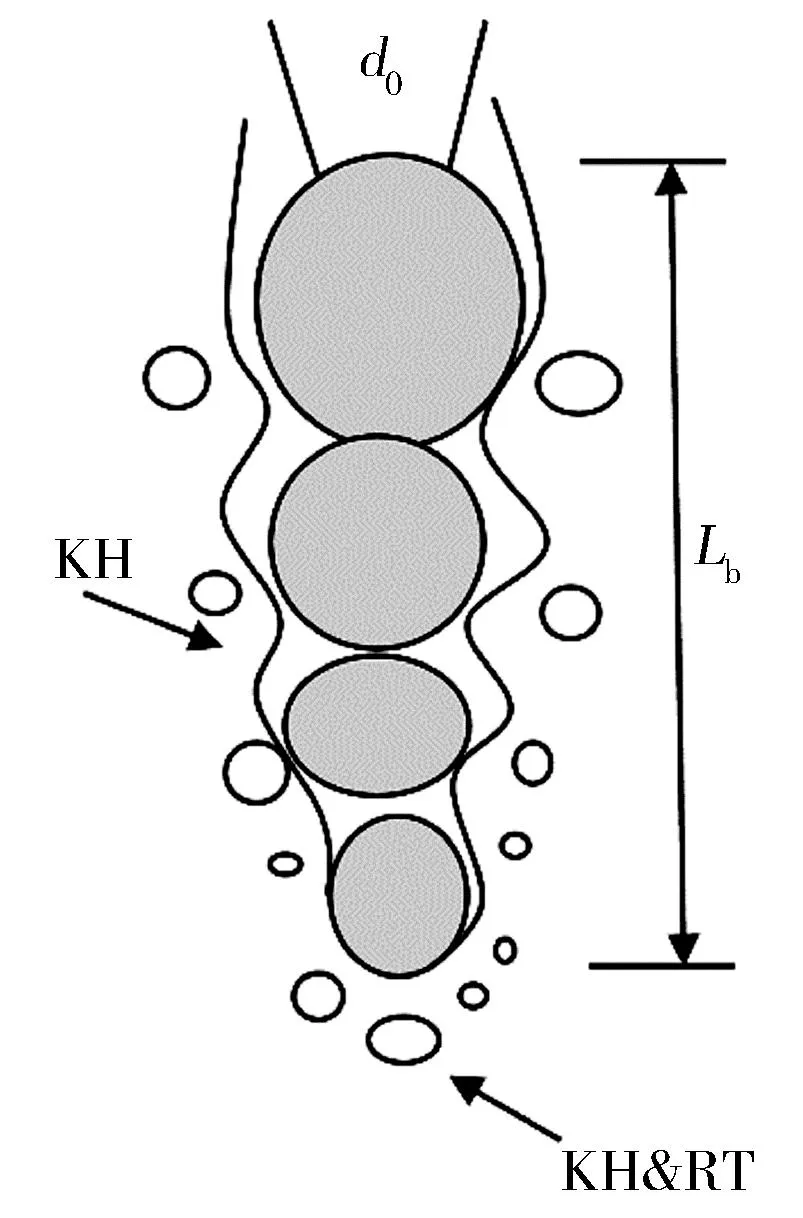
图2 KH-RT喷雾破碎模型示意

2 试验装置与方案

试验系统(如图3所示)利用复合激光诱导荧光(LIEF)技术同时量化了喷雾中的液相与气相分布。采用定容弹作为试验平台,结合真空泵和高压氮气充注系统,可将喷雾环境压力从20 kPa(绝对压力)调节到2 MPa。在喷油器周围安装了水套和热交换器,以控制燃料温度。利用蓄能器充注高压氮气,可产生高达20 MPa的燃油喷射压力。采用266 nm的Nd: YAG激光器作为激发光源,在通过圆柱形和球面透镜组合后形成厚度小于1 mm的片激光,然后经过喷油器轴线照亮喷雾截面。

图3 复合激光诱导荧光技术测试系统

本研究的基础燃料是正己烷,其中添加了两种示踪剂,即氟苯(FB)和二乙基甲基胺(DEMA)。己烷/FB/DEMA的体积比为89∶2∶9。CCD相机分辨率为1 376×1 040,拍摄频率为1 Hz,在其前端安装图像增强器,用以增强喷雾荧光信号,提高拍摄图片信噪比。由于两相荧光光谱之间存在光谱重叠现象,因此用两个光学带通滤波器进行了校正处理。

3 结果与讨论

3.1 仿真与试验结果对比

将仿真结果中的液相贯穿距数据导出,并与试验图像计算所得的贯穿距进行比较,得到的结果见图4。仿真结果中的贯穿距与试验图像计算所得数值的标准误差小于3%,因此认为两者吻合度较高。

图4 仿真与试验的液相贯穿距对比

使用图像处理软件识别试验图像并获得液相分布,并根据式(1)计算得到索特平均直径:

(1)

计算所得索特平均直径与仿真数据的对比见图5。根据蔡庆军等[9]的研究可知,两者的最大误差小于6 μm,因此可认为仿真和实测的索特平均直径基本吻合,仿真模型在液相上与真实情况吻合良好,验证了仿真模型的可行性。

图5 索特平均直径对比

根据Zhang等[10]和Düwel等[11]研究,400 K下气相荧光强度与对应的气相浓度基本呈线性关系。因此,可以通过对气相荧光强度进行测量,计算得出对应位置气相浓度的分布。根据此理论,由试验中的荧光强度测量结果计算出实际气相浓度,并与仿真结果对比,结果如图6所示。由图6可以看出,仿真的气相形态与试验结果相符。

图6 仿真与试验的气相浓度对比

然而,仿真模型在气相质量的计算结果上与试验结果出现了较明显偏差。气相质量的仿真结果、试验结果和两者之间的误差值见图7。由图7可见,在喷射初期,喷射时刻为0.3 ms之前仿真值与试验值吻合较好,但随着时间推移,仿真值与实际之间的差距逐渐变大。由图7中的气相质量误差曲线可知,误差值从0.4 ms开始迅速上升,在1 ms时,误差达到140%。

图7 气相质量对比与误差

以喷嘴垂直方向为中心轴,计算该方向上与喷嘴不同距离处的气相浓度,并将试验结果与仿真结果进行对比,为便于展示,取喷嘴距离30 mm与50 mm处的气相浓度进行对比,结果如图8所示。可以看出,在气相浓度的分布趋势上,试验结果与仿真是一致的,但是在浓度峰值附近,两者存在明显偏差,而且随着与喷嘴距离的增大,这种偏差也在增大。

图8 喷嘴不同距离处气相浓度对比

由以上结果可知,本研究中的喷雾数值仿真对于解决单一燃料组分中的喷雾蒸发问题具有可行性,液相部分与试验拟合良好,但气相部分存在明显误差。

3.2 液滴蒸发模型误差分析

在Converge软件中,蒸发问题的求解模型是基于单个液滴建立的,这意味着液滴周围所受影响特性的具体求解结果很大程度上取决于单个液滴的尺寸大小。因此,求解器给出两种方法来计算液滴随时间而产生的变化。其中,Frossling相关性模型使用经验方程去描述数值在径向上的变化,然后根据单个液滴的尺寸,计算热传递问题。当液滴半径大于临界值时,传热问题被转换为一个常微分方程。如果半径在临界值内,则转换为两个偏微分方程[12-17]。在该过程中,单液滴本身的传热和液滴向周围耗散的质量是影响燃料饱和蒸气压的关键因素。这些因素都会受到液相与气相边界变化的影响。

上述对于Frossling模型方程的分析基于没有发生沸腾的单一组分,但在进行复合激光诱导荧光的试验过程中,即使采用单一燃料,也无法避免示踪粒子的添加,此时会涉及到多组分和多相流的情况。从试验结果与仿真结果的对比可得出,蒸发模型并不能很好地模拟真实情况。因为在多组分和多相流的情况下,液滴的蒸发速率和破碎机制会受到不同液滴组分带来的影响,这可能会导致部分液滴参数逼近简化模型方程的边界值,从而使误差高于预期值。由于该模型的求解依赖单个液滴的参数,因此,破碎模型中的液滴尺寸是否符合实际情况中的液滴分布直接关系到仿真结果的正确性。

本次仿真过程中,Frossling模型在液滴径向尺寸r0大于临界值时,r0随时间t变化的经验方程转变为以下常微分方程:

(2)

式中:ρg为气相密度;ρl为液相密度;D为二维扩散系数;BM为Spalding质量转移系数;Sh为Sherwood数。

该模型中Sherwood数的值依赖以下关系式:

(3)

式中:Re为雷诺数;Sc为Schmidt数。因此结合式(1)和式(2)可知,r0的大小依赖Spalding质量转移系数BM。

在Frossling模型求解过程中,BM默认使用的是单液滴情况下仿真中燃料类型对应的经验数值。但是如果希望通过计算获得BM的数值,则存在以下关系式:

(4)

式中:YFs为燃料质量分数,下标s与∞分别代表液滴表面与外部气流的相关情况。在理想状态的单液滴情况下,YFs和YF∞是定值。然而对于实际喷雾,由于液滴与液滴之间存在强烈的质量传递,单液滴情况所假设的理想外部环境并不成立,所以YFs和YF∞的实际值会随着喷雾发展而不断产生变动。本次仿真中燃料多组分的情况可能加剧了YF的变动,导致BM值与实际偏差较大,从而使得式(2)的计算结果出错。

3.3 液滴蒸发模型误差修正

基于3.2节中对于仿真模型误差原因的分析,现针对Converge软件中Frossling模型的输入文件进行修改。取比例系数λ,范围设置为0.5～1.5,然后在该范围内等距取出100个λ值乘以原公式中的BM经验值,并代入模型输入文件的公式内进行仿真。将所有仿真结果进行对比后发现,当λ=1.02时,仿真与试验的气相质量对比误差最小,误差最大值为33%,相比第一次仿真的误差最大值140%有显著降低。具体数值曲线见图9。

图9 修改BM值之后的气相质量对比与误差

同时仿真得出的气相浓度与试验结果的吻合度相比第一次仿真也有较大提升,两次仿真的对比见图10。

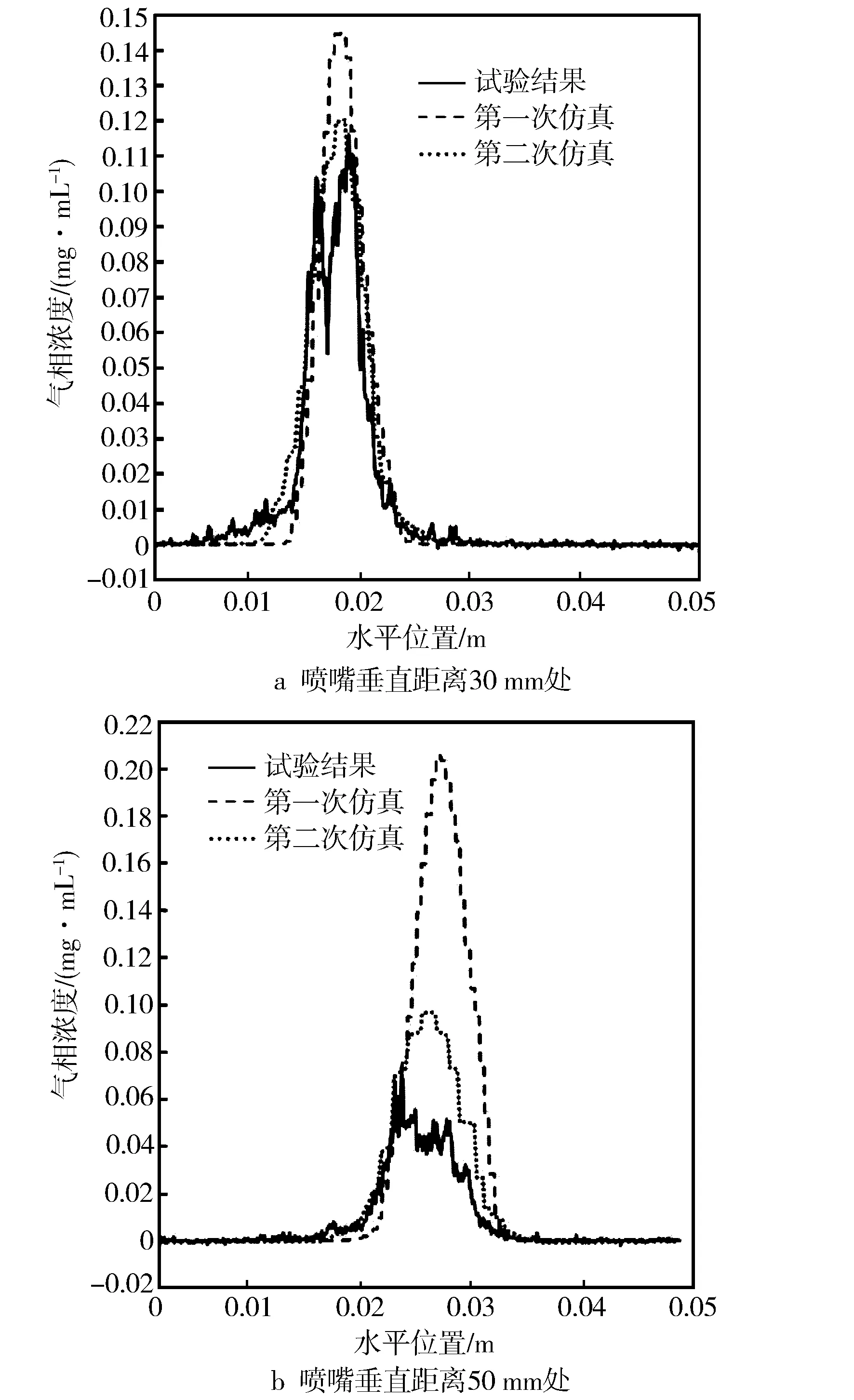
图10 修改BM值前后两次仿真的喷嘴不同距离处气相浓度对比

由于修改Spalding质量转移系数(BM值)使仿真精度得到明显提高,因此可以认为上文对于Frossling模型内部方程的分析与猜想是正确的。然而现有的BM值并不一定是最优解,后续可以通过数学手段进行二分逼近求解,此处不再讨论。另外提高仿真准确度的途径除了修正模型方程,还可以在现有的蒸发模型中引入新的因素,以控制多粒子的相互作用,或者直接引入新的模型,以更准确地预测液滴的蒸发和破碎机制。不同液滴的区域性变化会对气相质量产生很大影响,这些变化可能是由液滴破碎的随机性或者相近液滴之间的相互作用所产生的。在多组分和多相流的情况下,需要更精细地描述液滴之间的相互作用和破碎机制,以更准确地预测气相质量的变化。

虽然现有的蒸发模型存在一定的局限性,但通过对液滴破碎模型的调整和校准,仍然可以获得相对准确的仿真结果。在实际工程应用中,可以利用现有的模型对气相模型进行校准,以得到更精确的模拟结果。同时,结合LIEF技术进行气相校准试验的方法也是可行的,可以为液滴蒸发和破碎的研究提供更加准确的仿真结果。

4 结束语

基于商业CFD软件Converge内的Frossling模型建立了一个喷雾蒸发模型,使用该模型进行了冷态喷雾仿真,并使用复合激光诱导荧光与定容弹进行了相同条件下的试验,对仿真结果进行了验证。验证结果表明,仿真模型具有可行性,液相部分仿真效果较好,但气相部分出现明显偏差。

在喷雾蒸发模型仿真结果中,液相的贯穿距、索特平均直径均与试验结果呈现较高吻合度,但是在气相质量以及喷嘴轴线方向的气相浓度上出现了较明显的偏差,通过分析发现,这是由于仿真中采用的Frossling单液滴蒸发模型方程在多组分和多相流情况下无法准确判断气相喷雾的整体蒸发量。不同区域液滴破碎的随机性和液滴间的传质传热过程可能导致部分液滴的半径接近方程边界,使计算的误差超过预期值,最终导致仿真过程中的喷雾的蒸发和传热过程与实际情况产生明显偏差。通过分析Frossling模型方程,修正了经验方程参数,使误差显著降低。

尽管目前的喷雾数值仿真研究已经相对成熟,能够获取全面的数据结果,但数据的可信度并不能得到有效保证。由于Frossling单液滴模型在多组分和多相流的情况下可能会使部分区域的液滴参数逼近模型方程边界值,从而使误差高于预期值。因此,单纯依赖仿真数据是不可靠的,在使用仿真模型进行理论研究之前,有必要提前对模型进行校准,以保证研究的可行性与可靠性。在现实工程应用场景中,应该针对具体工况修正模型输入文件或者使用LIEF技术进行气相校准。