共轨喷油器高速电磁阀结构参数与响应时间耦合关系仿真研究及优化

徐丹,徐春龙,杨贵春,赵建辉,刘永旺,赵志帅

(1.中国北方发动机研究所(天津),天津 300406;2.哈尔滨工程大学动力与能源工程学院,黑龙江 哈尔滨 150001)

高压共轨燃油喷射系统可以灵活、柔性地调节喷射压力、喷油速率、喷油定时和喷油量,从而改善柴油机全工况范围内的综合性能,彻底解决了传统燃油喷射系统高低速时喷射压力差别过大、喷油量难以精确控制、喷油定时难以柔性调节等问题,目前已广泛应用于现代柴油机领域。高速电磁阀作为高压共轨燃油喷射系统共轨喷油器的核心零部件,是高压共轨燃油喷射系统能正常工作的最关键、最核心的部分,它承担着燃油的喷射控制功能,快速响应特性是衡量其工作性能的一个重要指标:通电时刻决定喷油定时,通电时长决定喷油量;快速开启保证喷油定时准确,快速关闭保证高压喷射的快速切断;同时,阀的快速动态响应特性是实现最小油量喷射和预喷射的系统硬件保证[1]。因此开展高速电磁阀结构参数与响应时间耦合关系研究,并在此基础上进行优化设计具有重要意义。

长期以来,国内外学者针对高速电磁阀动态响应特性开展了多方面的研究,包括电磁阀结构参数[2-5]、装配参数[6]、驱动电路[7-10]、组件结构[11]等对动态响应特性的影响。上述研究主要集中在电磁阀各参数对其动态响应特性的影响规律分析上,而未对各参数对动态响应影响的敏感性进行研究,且将各参数与响应时间进行耦合的仿真分析及优化研究较少。本研究首先建立耦合驱动电路的高速电磁阀动态响应计算模型;其次以计算模型提供的样本矩阵为基础,结合D-optimal设计与最小二乘法,采用RSM数学近似模型建立高速电磁阀响应时间的响应面预测模型,基于预测模型开展结构参数元效应敏感性分析工作;最后通过NBI-AFSQP优化算法,以提高高速电磁阀响应速度为优化目标,对高速电磁阀结构参数进行优化设计。

1 高速电磁阀工作原理与数学模型

1.1 工作原理

本研究的共轨喷油器高速电磁阀具体结构见图1,主要由衔铁、衔铁复位弹簧、线圈、铁芯、阀杆、球阀、阀座、衔铁缓冲弹簧、电磁阀壳体和电磁阀体等组成。

图1 共轨喷油器高速电磁阀结构示意

电磁阀线圈通电后,铁芯迅速产生足够的电磁吸力,吸合衔铁克服电磁阀复位弹簧的预紧力,快速上移,球阀在控制腔高压燃油的作用下脱离球阀座,出油节流孔开启,控制腔燃油卸压,针阀在向上合力的作用下抬起,实现共轨喷油器喷油;电磁阀断电后,电磁力迅速消退,电磁阀复位弹簧推动衔铁向下运动,使球阀落座关闭出油节流孔,控制室内燃油压力迅速回升,针阀在向下合力的作用下迅速落座,共轨喷油器结束喷油。

1.2 数学模型

高速电磁阀在工作过程中主要包含阀杆及衔铁的机械运动(不考虑球阀运动及喷油器控制腔燃油压力)、线圈及铁芯处的电磁转换等过程,主要可划分为5个阶段:磁吸运动阶段、磁吸接触阶段、通电保持阶段、释放接触阶段和释放运动阶段[12]。分析电磁阀工作过程的5个阶段,用电路方程、磁路方程及运动方程简要概况整个过程。

1) 电路方程

在电磁阀开启和保持阶段驱动电路供电,此时线圈电路的电压U等于线圈电路的等效电阻电压加上电路中总的感应电压,具体方程如下:

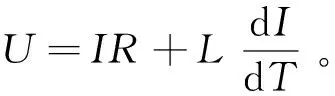
(1)

式中:U为线圈电压;I为线圈电流;R为线圈电阻;L线圈电感。

2) 磁路方程

三维静磁场中基本麦克斯韦方程组如下:

*H(x,y,z)=J(x,y,z),

(2)

*B(x,y,z)=0。

(3)

式中:H(x,y,z)为磁场强度;J(x,y,z)为电流密度;B(x,y,z)为磁感应强度。

3) 运动方程

运动部件工作过程中主要受到电磁力、弹簧压力、重力、燃油压力以及摩擦力作用,根据牛顿运动学定理,具体机械运动方程可以表述为

(4)

式中:F(t)为电磁力;Fhyd(t)为燃油作用力;η为摩擦系数;k为弹簧刚度;F0为弹簧预紧力;mg为运动部件重力。

2 耦合驱动电路的高速电磁阀动态响应计算模型构建及校核

2.1 高速电磁阀磁场三维仿真模型构建

主要研究工具为高速电磁阀响应时间的响应面预测模型,为了给预测模型待定系数的确定提供一定数量的样本矩阵,提高高速电磁阀动态响应预测精度以开展后续研究工作,本研究首先建立高速电磁阀磁场三维模型。由于所研究的共轨喷油器高速电磁阀为对称结构,为减小计算量,仅选择电磁阀结构的1/2为磁场三维建模分析对象。在建模过程中,忽略复位弹簧、阀杆、外壳等非磁性材料,仅考虑铁芯、衔铁等磁性材料以及线圈,且不考虑磁性材料的磁滞效应以及运动部件的弹性碰撞。

在高速电磁阀模型参数设置中,设定磁性材料为GCr15,弹簧预紧力为F0=60 N,电磁阀部件最大气体间隙为0.1 mm,线圈匝数为X1=50。采用Ansoft仿真软件建立高速电磁阀磁场三维模型(见图2)。

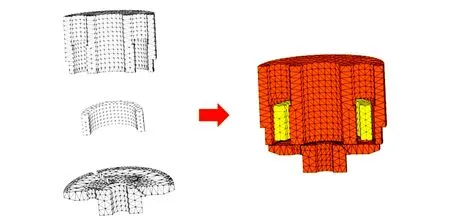
图2 高速电磁阀磁场三维仿真模型及网格划分

2.2 耦合驱动电路的高速电磁阀动态响应计算模型

为实现高速电磁阀更好的响应特性,通常采用peak-hold电流反馈驱动[12]:在磁吸上升阶段供给高电压,线圈内形成大驱动电流,加快电磁力的增加,实现更快的开启响应;在通电保持阶段,供给低电压,形成较低的保持电流,实现电磁阀的稳定开启,该驱动方式不仅可以降低功耗,而且可以显著改善电磁阀的发热现象;在高速电磁阀关闭阶段,为使其快速退磁,供给大的负向电压,从而使球阀快速落座,实现更快的关闭。

Ansoft软件自带电路模型较简单,无法实现peak-hold电流反馈。而Simplorer是一款机电系统设计与模拟仿真软件,该软件内嵌了大量的元器件库,能够实现建立复杂控制电路模型的需求,因此本研究采用Ansoft软件与Simplorer软件联合仿真的方法,根据电磁机耦合原理,将Simplorer软件建立的带有电流反馈的高速电磁阀驱动电路(包括电压源、高/低压控制开关、功率开关、采样电阻、电感、二极管等)与Ansoft软件建立的高速电磁阀磁场三维仿真模型进行耦合,建立了耦合驱动电路的高速电磁阀动态响应计算模型(如图3所示)。

图3 耦合驱动电流的高速电磁阀动态响应计算模型

2.3 模型校核验证

图4示出高速电磁阀动态响应特性测试试验台,包括电源控制单元、电流驱动控制单元、霍尔式位移传感器和数据采集单元,可进行最大驱动电流为25 A及位移范围为0～90 μm的高速电磁阀动态响应特性测试试验。

图4 高速电磁阀动态响应测试装置

图5示出高速电磁阀动态响应仿真计算结果与高速电磁阀试验台测试结果的数据对比。通过对比可知,在一个工作循环内,电流和衔铁升程的仿真数据与试验数据具有较高的吻合程度,试验值与仿真值的误差范围为0≤δ≤5%,验证了该仿真计算模型的准确性,利用仿真模型能够较准确地对高速电磁阀动态响应特性进行仿真计算,可采用此模型进行后续研究工作。

图5 仿真数据与试验数据比较

3 高速电磁阀响应时间预测模型及结构参数影响敏感性分析

3.1 高速电磁阀响应时间的响应面预测模型构建

在探究优化目标与优化参数耦合关系时,常常采用数学方法建立近似模型,这样可以大幅减少计算工作量。响应面模型作为一种数学近似模型,最早由BOX和Wilson提出,是一种用于开发、改良、优化的统计和数学方法,可以建立起目标、约束与设计变量之间的近似函数。响应面模型具有试验次数少、模型预测精度高和预测性能好的优点,在工程研究中得到广泛的应用。常用的数学近似模型包括RBF模型、RSM模型、Kriging模型等,本研究采用RSM数学近似模型建立高速电磁阀结构参数与响应时间的耦合关系。根据工作实际,响应面函数通常选取线性、二次多项式、三次多项式的形式,在满足精度的前提下为减少计算成本,本研究选取的响应面函数为二次多项式形式,具体方程如下[13]:

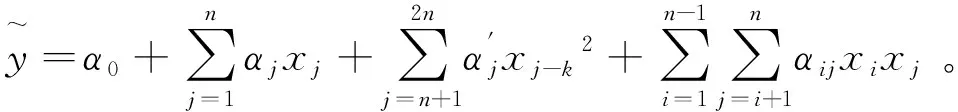
(5)

式中:α0为常数项待定系数;αj为一次项待定系数;αj′为平方项待定系数;αij为二次交叉项待定系数;xj为单次项;xi-j2为平方项;xixj为二次交叉项;n为变量数量;k为参数维数,k=n。

建立响应面预测模型时选取的高速电磁阀关键结构参数为线圈匝数、衔铁升程、内磁极半径、外磁极半径以及衔铁半径,响应时间分别为开启响应时间(从驱动电流给电时刻到衔铁升程达到最大位置时刻之间的时间)与关闭响应时间(从驱动电流断电时刻到衔铁完全落座之间的时间),因此分别建立两者的响应面数学预测模型。高速电磁阀关键结构参数基准值与取值范围见表1。

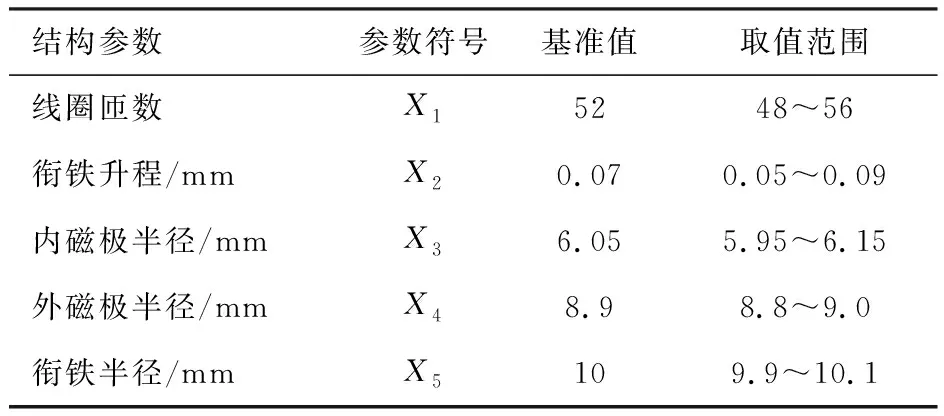
表1 高速电磁阀关键结构参数基准值与取值范围

为确定响应面函数的待定系数,需准备一定数量的样本矩阵,样本的选取应遵循只需少量取样点就能得到较高精度响应面函数的原则。本研究采用D-optimal设计,在保证计算精度的前提下尽可能地减少计算次数,同时综合各结构参数的取值水平,保证样本矩阵行列式值最大,使计算数据更为合理,构建的响应面预测模型更为准确。仿真计算矩阵、开启响应时间To及关闭响应时间Tc见表2。

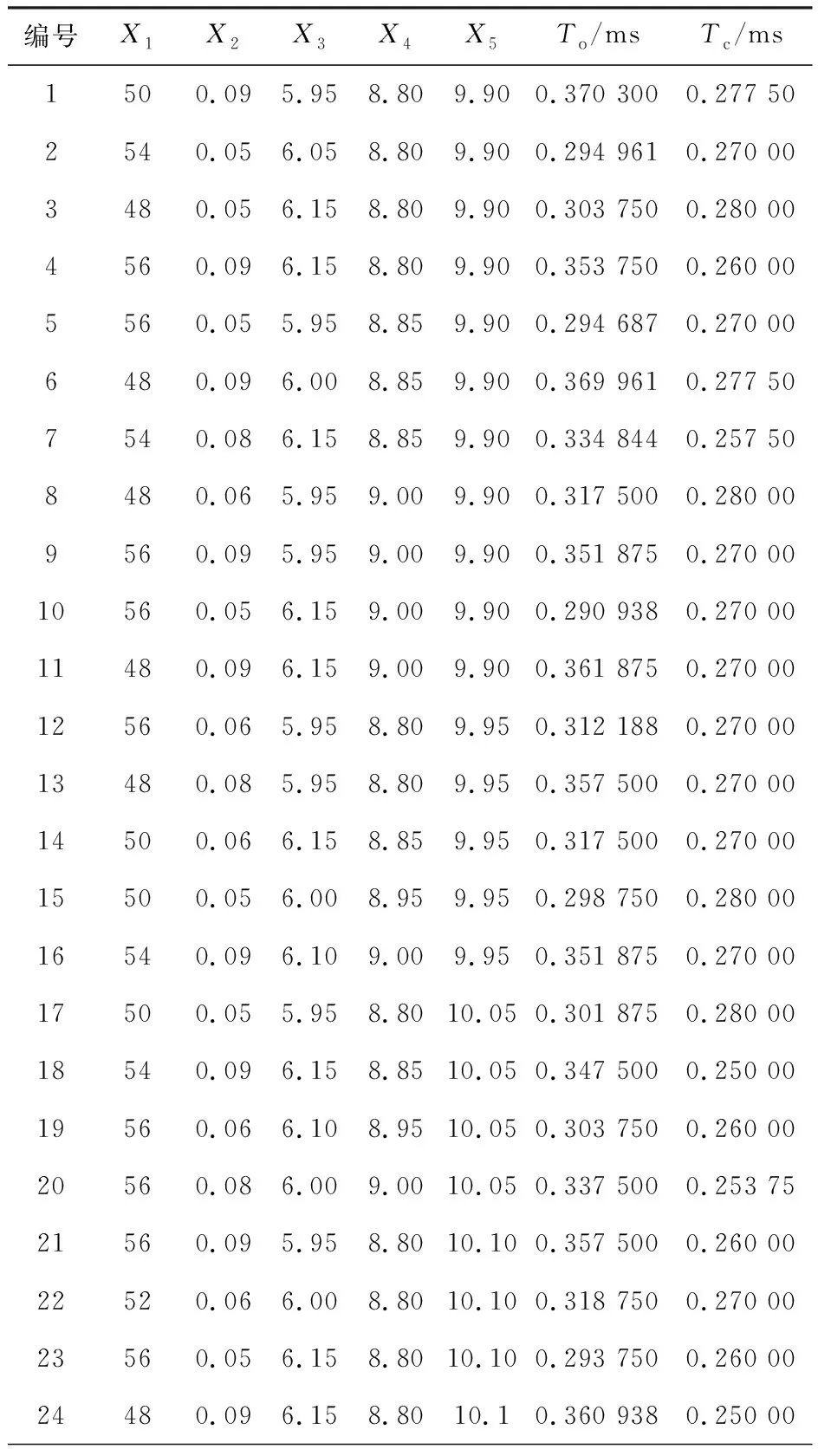
表2 仿真计算矩阵及响应时间

根据表2所得数据,采用最小二乘法,经过数学计算求解得到待定系数α0,αj,αj′,αij,开启响应时间To和关闭响应时间Tc的响应面函数具体如下:

To=f(X1,X2,X3,X4,X5)=-8.072 01-0.018 34X1+12.686 06X2+1.049 26X3-4.352 15X4+1.740 35X5=+0.000 054X12-2.403 06X22-0.060 72X32+0.231 822X42-0.067 95X52=-0.016 21X1X2-0.000 15X1X3+0.000 045X1X4+0.001 292X1X5=-0.762 34X2X3-0.170 54X2X4-0.385 56X2X5=+0.041 843X3X4-0.065 01X3X5-0.004 3X4X5,

(6)

Tc=f(X1,X2,X3,X4,X5)=-33.522 7+0.056 35X1+22.682 78X2+2.091X3-3.070 31X4+7.845 16X5=-0.000 083X12+17.336 44X22-0.071 54X32+0.182 123X42-0.322 52X52=+0.011 121X1X2-0.001 44X1X3-0.003 44X1X4-0.001 05X1X5=-1.244 72X2X3-0.250 76X2X4-1.622 29X2X5=+0.059 052X3X4-0.163 35X3X5-0.032 01X4X5。

(7)

根据图6、图7中开启响应时间与关闭响应时间的预测值与仿真值对比可知,预测值和仿真值整体分布在函数y=x附近。

图6 To预测值与仿真值比较

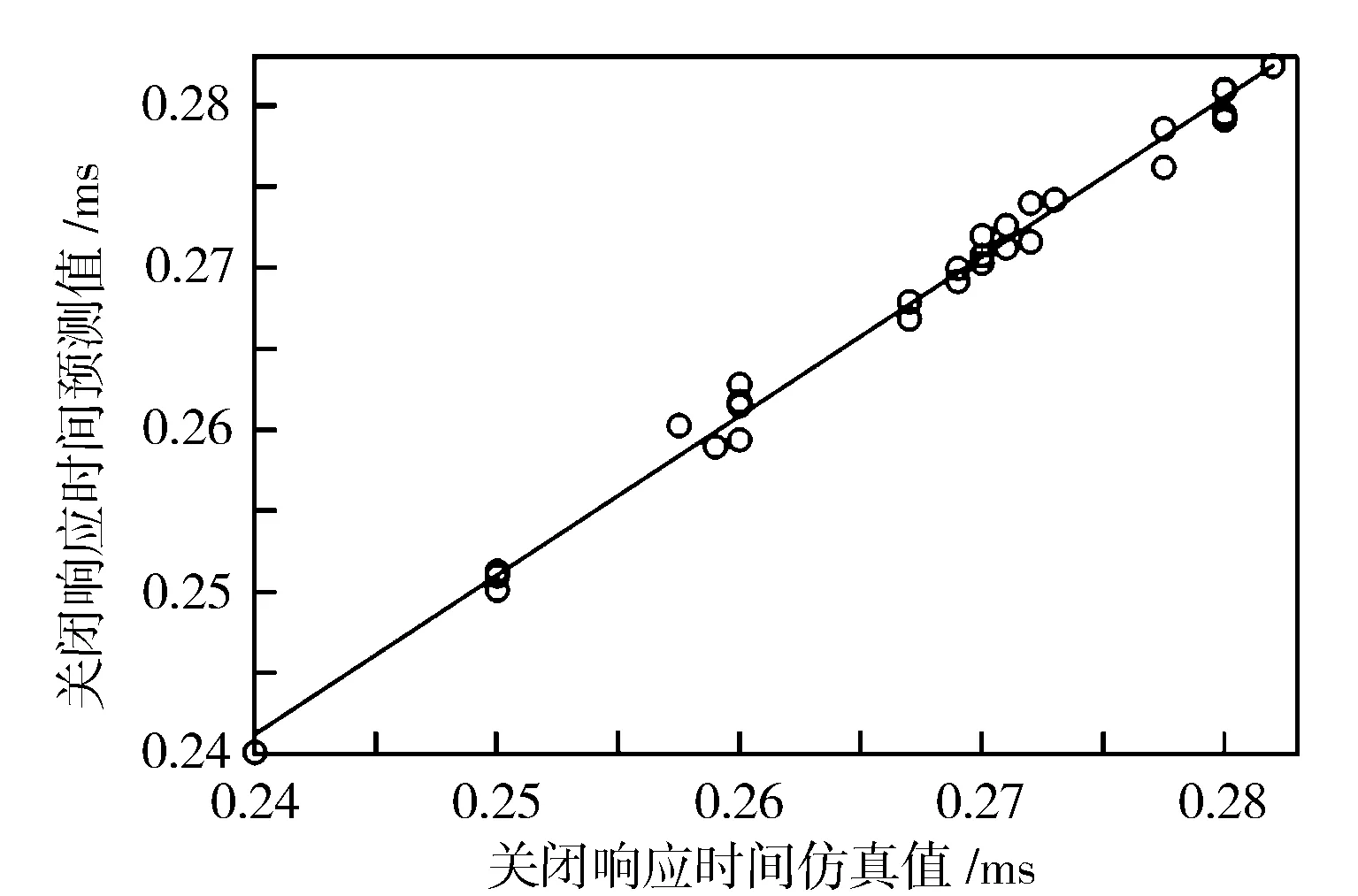
图7 Tc预测值与仿真值比较

此外引入评价指标复相关系数R2,R2是反映模型拟合程度的一种重要指标,表示模型的预测准确性,R2越接近于1说明误差影响越小,方程越准确,一般认为R2超过0.8的模型拟合优度较高[15-16]。通过计算得到开启响应时间的复相关系数R12=0.991 2,关闭响应时间的复相关系数R22=0.965 3,两个复相关系数非常接近于1,由此说明本研究建立的响应面预测模型的正确性,可以利用该模型进行后续研究及参数优化。

3.2 高速电磁阀结构参数对响应时间影响的敏感性分析

引入基于元效应的全局敏感性分析方法进行高速电磁阀结构参数的敏感性分析。元效应方法的中心思想是在一个k维参数空间提取各个变化参数的元效应值,并通过对元效应值进行期望、方差分析,最终得到全局敏感性指标。对于第i个输入参数Xi,其元效应值EEi表达式为

EEi=[Y(X1,X2,…Xi-1,Xi+Δ,…Xk)-Y(X1,X2,…Xk)]/Δ。

(8)

式中:Δ为第i个输入参数的改变量。

Campolongo等[17]提出了将元效应绝对值分布的均值估计作为参数敏感性强弱的度量,表达式如下:

(9)

式中:r为采样层数。

针对表1中列出的5个高速电磁阀关键结构参数,将5个输入参数在k=5维单位立方体中通过r=20个采样层进行变化,响应时间样本计算矩阵及响应时间预测值见表3。

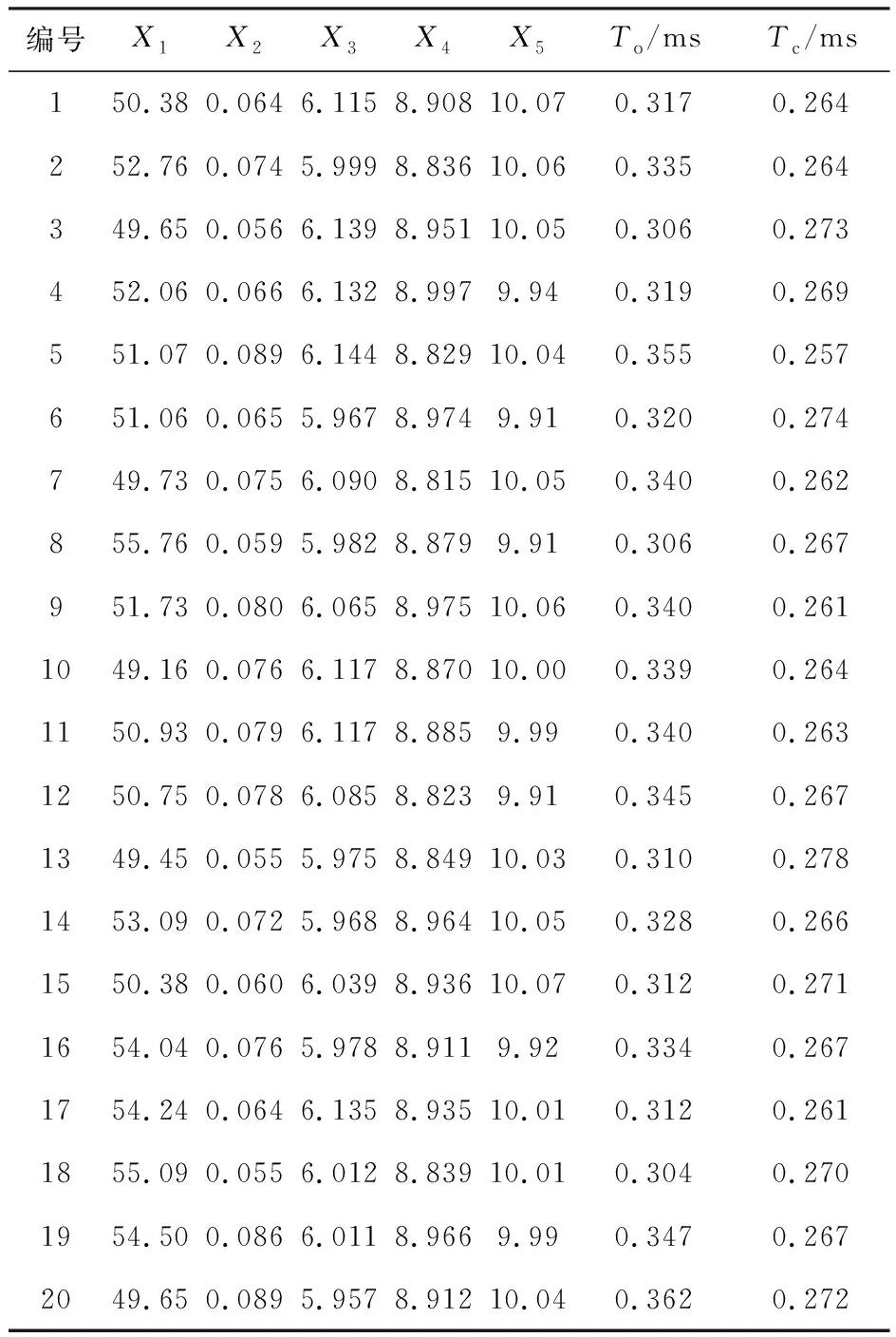
表3 响应时间样本计算矩阵及响应时间预测值

在本研究中根据实际情况取Δ=0.05,利用式(8)、式(9)计算出各个参数的敏感性指标μ*,根据μ*的大小确定各结构参数敏感性,分类原则[18]为

计算得出各结构参数对于开启响应时间的敏感性指标μ1*和关闭响应时间的敏感性指标μ2*,如表4所示。

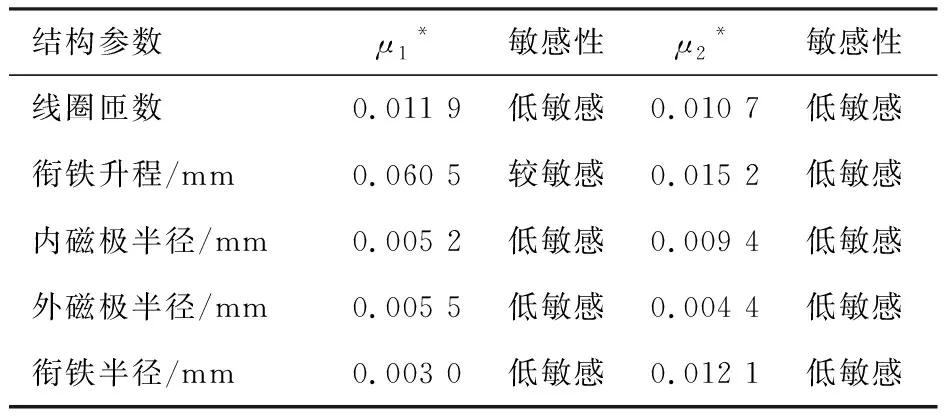
表4 各参数μ*计算值与敏感程度

从表4数据可以看出,衔铁升程对于开启响应时间的敏感性指标μ1*=0.060 5,为开启响应时间的较敏感参数,其余参数为低敏感参数。在开启响应时间的低敏感参数中,线圈匝数对开启响应时间的敏感性最高,衔铁半径的敏感性最低。此外衔铁升程对关闭响应时间的敏感性最高,外磁极半径敏感性最低。因此在进行高速电磁阀正向设计时应格外注意衔铁升程的选取。

为验证元效应敏感性分析结果的正确性,针对较敏感参数变化与低敏感参数变化进行1 000次仿真计算,得到开启响应时间的计算结果分布,如图8所示。当较敏感参数衔铁升程在参数范围内变化,其余低敏感参数为基准值时,开启响应时间变化范围较大,最大差值为0.06 ms;当低敏感参数变化,较敏感参数衔铁升程取基准值时,开启响应时间分布比较集中且变化范围较小,与较敏感参数变化时对比存在明显的分层现象。因此可验证敏感性分析结果的正确性。

图8 不同敏感性参数变化下To分布

3.3 较敏感结构参数对响应时间的影响

由上节可知,衔铁升程为开启响应时间的较敏感参数,因此对该参数进行单独分析。衔铁升程取0.05 mm,0.06 mm,0.07 mm,0.08 mm及0.09 mm五种水平,其余参数取值为基准值,得到不同开启响应时间(见图9)。随着衔铁升程增加,高速电磁阀开启响应时间随之延长,从图9可以看出,衔铁升程从0.05 mm增加至0.09 mm,开启响应时间相应地增加了约20.6%。这是因为在高速电磁阀打开阶段,衔铁升程增加导致到达上止点时间增加,此外电磁力也存在衰减,高速电磁阀打开速度下降,导致开启响应时间延长。

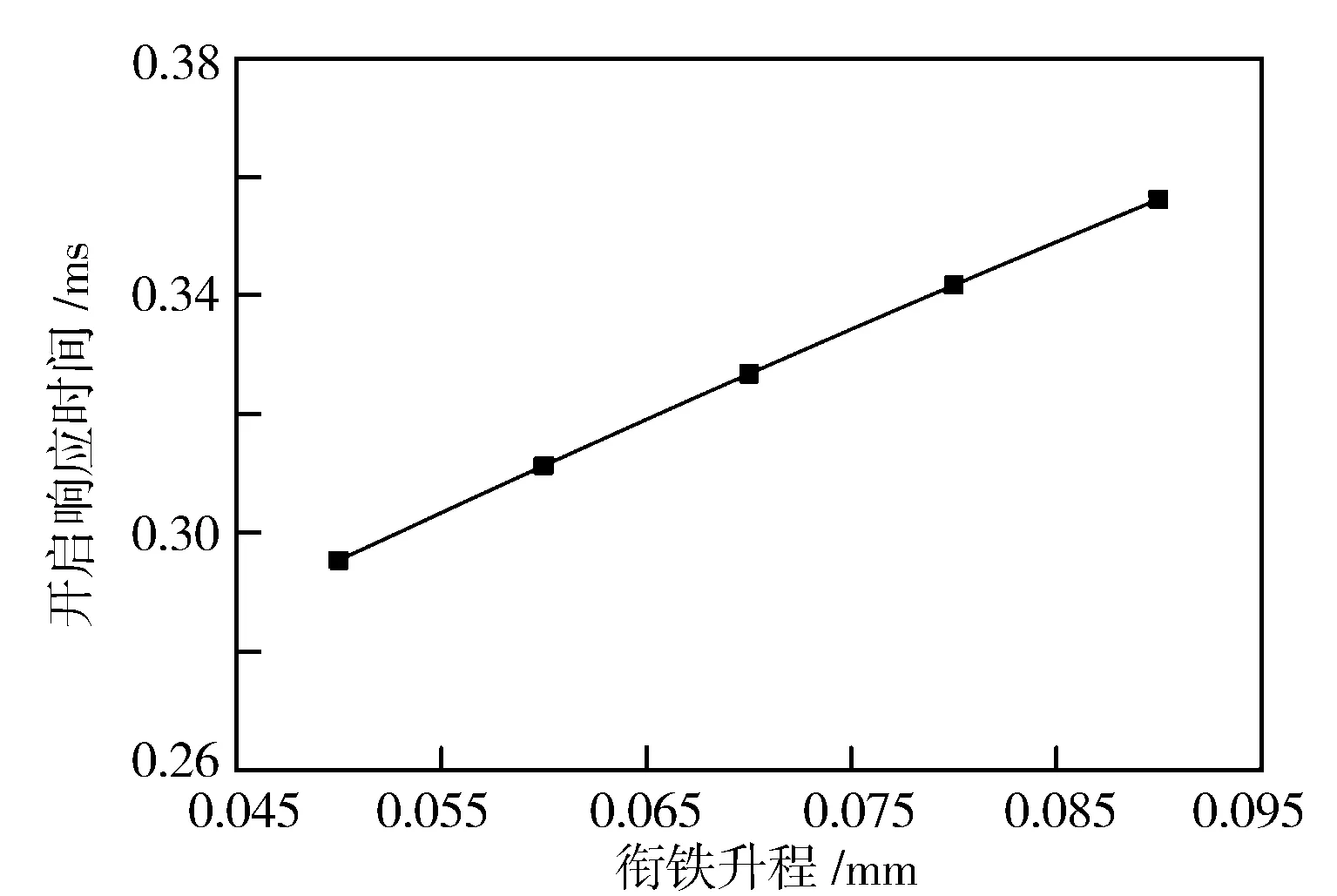
图9 衔铁升程对开启响应时间的影响

4 高速电磁阀结构参数优化设计

4.1 优化算法及数学模型

利用响应面预测模型可以确定高速电磁阀结构参数与响应时间的耦合关系,获得不同结构参数对应的响应时间。进行高速电磁阀结构参数优化设计时,以优化算法的优化目标及约束为条件,利用预测模型对不同结构参数的响应时间进行仿真计算,确定满足优化算法条件的高速电磁阀结构参数。

高速电磁阀结构参数优化设计目标为降低开启响应时间To和关闭响应时间Tc,但二者有时存在冲突性,To的缩短可能会引起Tc的增加,同时使To和Tc达到最小值是很难实现的,因此取二者之和作为总响应时间T,通过三者之间的协调权衡和折中处理使三者尽可能同时达到最优。

本研究基于由I. Das和J. E. Dennis开发的法向边界相交(Normal Boundary Intersection)方法[19],并结合专有的AFilterSQP算法,形成多目标梯度的优化算法NBI-AFSQP。该算法用于解决任何一般光滑多目标问题,将其简化为多个单目标约束子问题,称为NBI子问题,每个子问题都用AFSQP单目标算法求解。

首先对优化目标参数进行数学描述。确定优化变量及其取值范围,选取线圈匝数X1、升程X2、内磁极半径X3、外磁极半径X4以及衔铁半径X5作为优化变量,则数学模型及变量约束如下:

minT(x)=(To,Tc,T),

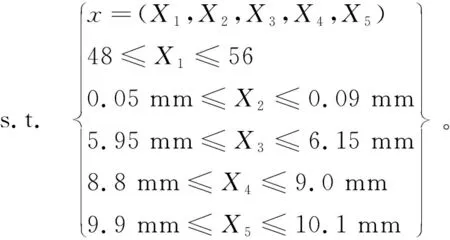
(10)

4.2 结果讨论

利用NBI-AFSQP算法对高速电磁阀结构参数进行优化设计,在迭代200次后优化变量趋于稳定,图10至图12分别示出线圈匝数X1、衔铁升程X2和内磁极半径X3在迭代过程中的变化趋势。

图10 线圈匝数迭代变化过程

由图10可知,线圈匝数X1在迭代过程中寻找到的最优解为56,与优化前的54相比有所增加,原因在于随着线圈匝数的增加,高速电磁阀在工作过程中产生的电磁力随之增加,使得衔铁的运动速度加快,从而缩短了开启响应时间To。

由图11可知,衔铁升程X2在迭代过程中寻找到的最优解为0.06 mm,与优化前的0.07 mm相比有所减小。这是因为衔铁的运动行程减小,在高速电磁阀打开和关闭阶段可以更快地达到行程终点,缩短了响应时间。

图11 衔铁升程迭代变化过程

由图12可知,内磁极半径X3在迭代过程中寻找到的最优解为6.15 mm,与优化前的6.05 mm相比有所增加。这是因为内磁极半径X3增加使得内磁极面积增大、磁通量增加,高速电磁阀产生更大的电磁力,减小了开启响应时间To。

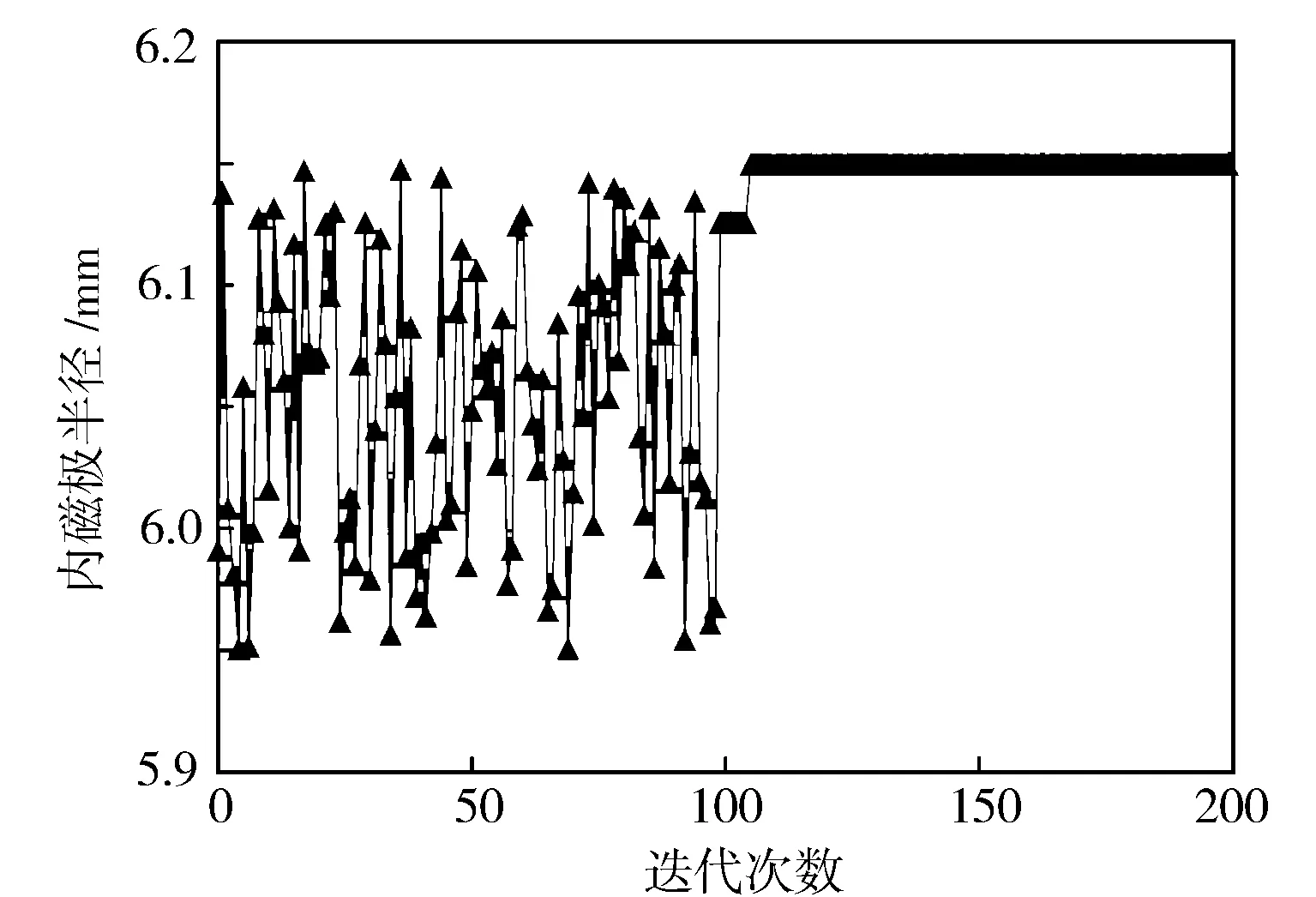
图12 内磁极半径迭代变化过程

根据各优化变量迭代后的最优解对高速电磁阀仿真计算模型进行调整,计算出高速电磁阀优化后的响应时间。图13示出高速电磁阀结构参数优化前后衔铁升程曲线的对比。由图13可以看出,开启响应时间To有较小程度的缩短,关闭响应时间Tc有较大程度的缩短。

图13 高速电磁阀结构参数优化前后衔铁升程曲线的对比

表5列出高速电磁阀结构参数及响应时间优化前后的对比,开启响应时间To与优化前相比减小了6.25%,关闭响应时间Tc减小了9.56%,总响应时间减小了7.64%。

表5 优化前后高速电磁阀的响应时间对比

5 结束语

采用Ansoft软件与Simplorer软件联合仿真,构建了耦合驱动电路的高速电磁阀动态响应计算模型,通过试验数据与仿真数据对比验证了计算模型的准确性,可为后续高速电磁阀响应时间的响应面预测模型待定系数的确定提供样本矩阵。

采用D-optimal设计与最小二乘法,构建了高速电磁阀结构参数与响应时间之间的RSM数学近似模型,同时基于RSM模型,利用元效应敏感性分析方法,开展了高速电磁阀结构参数对响应时间的敏感性研究,确定了衔铁升程是开启响应时间的较敏感参数,在高速电磁阀正向设计过程中应谨慎选择。参数对开启响应时间的敏感性由大到小依次为衔铁升程,线圈匝数,外磁极半径,内磁极半径,衔铁半径;参数对关闭响应时间的敏感性由大到小依次为衔铁升程,衔铁半径,线圈匝数,内磁极半径,外磁极半径。

使用NBI-AFSQP优化算法,以提升响应时间为优化目标,对高压共轨电控喷油器高速电磁阀的结构参数进行了优化设计,优化结果表明,高速电磁阀开启响应时间降低了6.25%,关闭响应时间降低了9.56%,总响应时间降低了7.64%。