高温下掺氢燃气层流燃烧速度和稳定性研究

朱源,姜根柱,王筱蓉,苏傲成

(江苏科技大学机械工程学院,江苏 镇江 212003)

传统化石燃气造成的环境污染、温室效应和能源危机已引起全世界的广泛关注。目前,人们正在积极寻找替代燃气并开展可再生燃气的研究。氢气和乙醇作为具有优良性能的替代燃气受到了广泛关注。氢燃气可以代替化石燃气作为发动机燃气。因为氢气燃烧后的排放物是水,所以其对环境的污染几乎为零;氢气具有较高的自燃温度,因此可更适用于作火花点火式发动机的燃气;此外,氢气还具有易于制备的优点。然而,随着对氢气的深入研究,氢气的缺点也随之显现。其一,氢的爆炸极限低,属于极易爆炸能源;其二,氢气的燃烧过程相对不稳定,限制了其能成为替代燃气的发展。与此同时,相关研究发现,通过严格控制工作温度、压力以及在氢气中掺入一定量的低能量密度的燃气,可以有效地改进氢气燃烧过程中不稳定的情况。而与其他各种碳氢化合物(链烷烃、芳烃、烯烃、环烷烃)相比,乙醇可以更好地提升内燃机的输出功率和热效率,还可以减少有害污染物的排放[1]。因此,有必要对高温下掺氢燃气(氢气-乙醇-空气)的燃烧特性进行研究。

层流燃烧速度(LBV)是一种重要的热化学性质,它表征了可燃燃料-空气混合物,并提供了有关给定燃料及其混合物的反应性、扩散性和放热性的重要信息。目前,诸多学者已经开始对含乙醇混合气的层流燃烧特性进行研究。

Zhang Zunhua等[2]考察了初始温度为383 K,初始压力为0.1 MPa,当量比为0.6～1.6下,0～80%氢气含量的75%含水乙醇-氢气-空气混合气的主要层流火焰特性,通过比较SRE燃料空气火焰与乙醇火焰的层流燃烧速度、绝热火焰温度以及Markstein长度,发现促进SRE燃料高效燃烧的最适合的氢分数值为40%。Zhou等[3]在初始温度为400 K,初始压力为0.1～0.3 MPa,当量比为0.7～1.4下,研究了乙醇掺混10%～30%氢气对LBV的影响,结果表明,层流燃烧速度与氢气掺混量是正相关关系,增大压力则会抑制其发展,氢气的加入可以显著提高乙醇-氢气-空气火焰的绝热火焰温度。Xu Cangsu等[4]研究了初始温度为358 K,初始压力为0.1 MPa,当量比为0.5～1.4下的氢气(0%,4%,8%和12%)-乙酸乙酯混合燃料的层流燃烧特性,结果表明,乙酸乙酯的LBV随着H2添加量的增加而增强,并且氢气延长了当量比的可燃性的下限。Tian Zhi等[5]比较了不同醇氢(甲醇/氢气,乙醇/氢气以及丁醇/氢气)混合物在TISI发动机中的性能,发现醇氢混合物可以用来降低HC,CO和CO2排放。张嘉玮等[6]系统地研究了初始温度400 K工况下,不同初始压力(0.1 MPa,0.4 MPa),不同掺氢量(0%,10%,30%,50%,70%和90%)以及不同当量比(0.7～1.4)对乙醇层流燃烧特性的影响,试验结果表明:提高掺氢量对于LBV有促进作用,升高初始压力虽然对LBV有抑制作用,但提高了LBV的增长速率。Sven Eckart等[7]在恒定大气压、初始温度为373 K、不同当量比(0.6～1.7)下,对二甲醚-氢气混合物进行了全面分析,发现氢气的加入改善了二甲醚-空气混合物的整体燃烧特性,提高了火焰温度、LBV以及燃烧效率。然而,目前对于高温下乙醇掺氢混合燃气的层流燃烧特性的相关研究甚少。

鉴于目前研究的不足,本研究利用定容燃烧弹对初始温度为450 K,初始压力为0.2 MPa,氢气含量为50%,70%和80%,当量比为0.7～1.4时的氢气-乙醇-空气混合燃气进行了试验和数值研究。采用球形火焰扩散法研究了拉伸对火焰的影响,得到了Markstein长度和层流燃烧速度,并拟合出计算H2-C2H5OH-Air预混燃气LBV的经验公式。

1 试验装置和混合燃料

试验装置如图1所示,主要由定容燃烧室、进气和排气系统、加热装置、高速纹影成像系统、点火系统和数据采集系统组成。

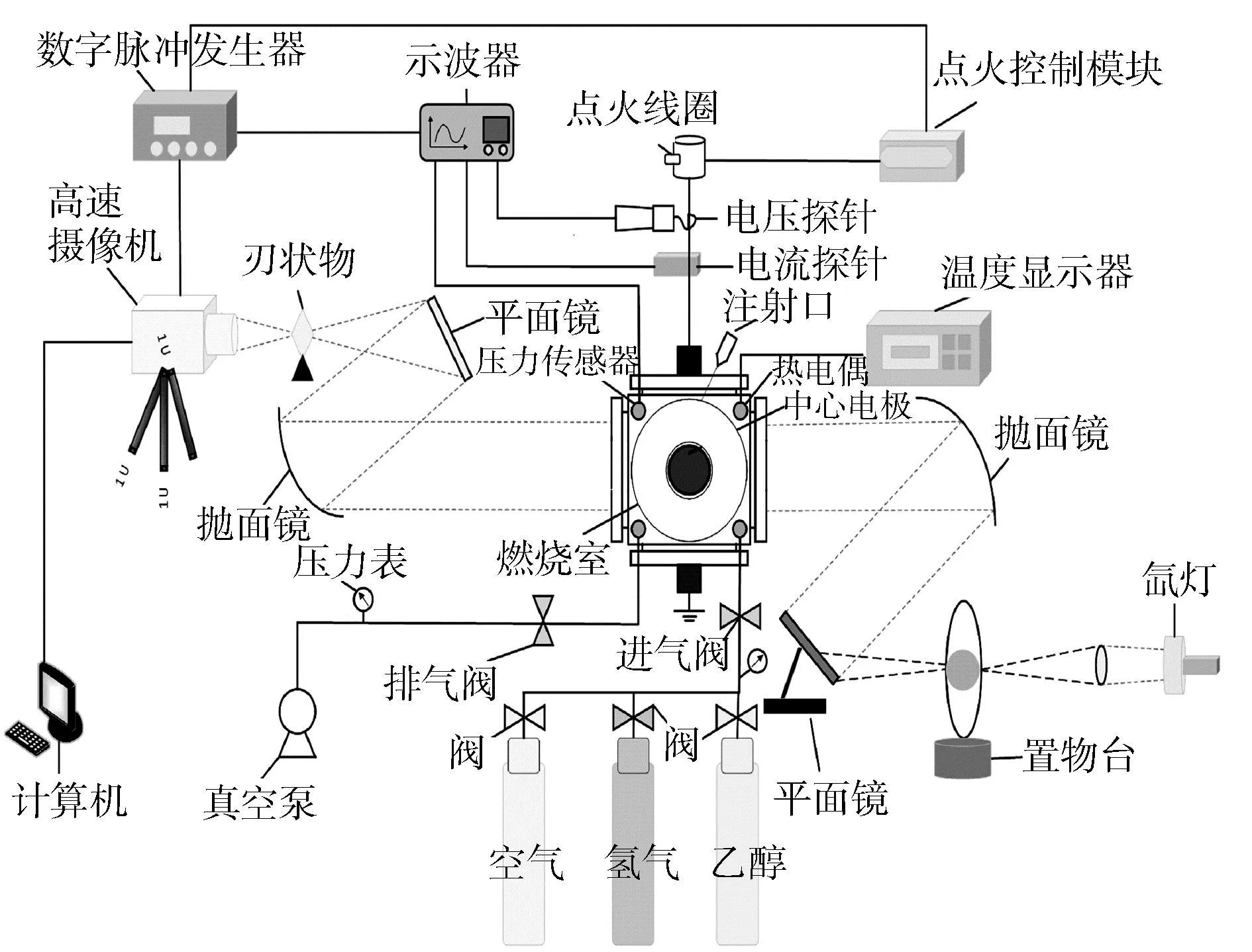
图1 试验装置系统

图2示出定容燃烧弹的实体,是似正方体结构,视窗直径为90 mm,容积为2.067 L。试验前要检查装置的气密性。K型热电偶与温度显示器结合用于监测温度,为保证弹体内温度的均匀与稳定,本研究采用的加热方式为壁面电阻加热。压力传感器用来实时监测容器内的压力。点火装置以15 mJ的点火能量对处于容器中心的两根铂丝电极进行电火花点火,引燃燃气。数字脉冲发生器与高速摄像机和示波器相连,高速摄像机以12 800 帧/s的拍摄速度和1 024×1 024像素的分辨率来记录0.1 s内完成的火焰燃烧过程,示波器用于记录信号,试验过程中要保证点火装置、高速摄像机以及示波器同步触发。

图2 定容燃烧弹外廓

表1列出氢气与乙醇的基本属性。由于本次设定的试验温度是450 K,超过乙醇的沸点,所以在将乙醇注射到定容弹后,可以由液态转为气态,故在该温度下进行的试验是有效的。

表1 氢气与乙醇的基本属性

由于本试验所用的燃料是由H2,C2H5OH和空气严格按比例混合而成,所以它们反应的化学表达式可表示为

(1)

本试验的燃气和工况如表2所示。根据当量比的变化,将φ<1规定为贫燃状态,φ=1规定为化学计量比,φ>1规定为富燃状态。

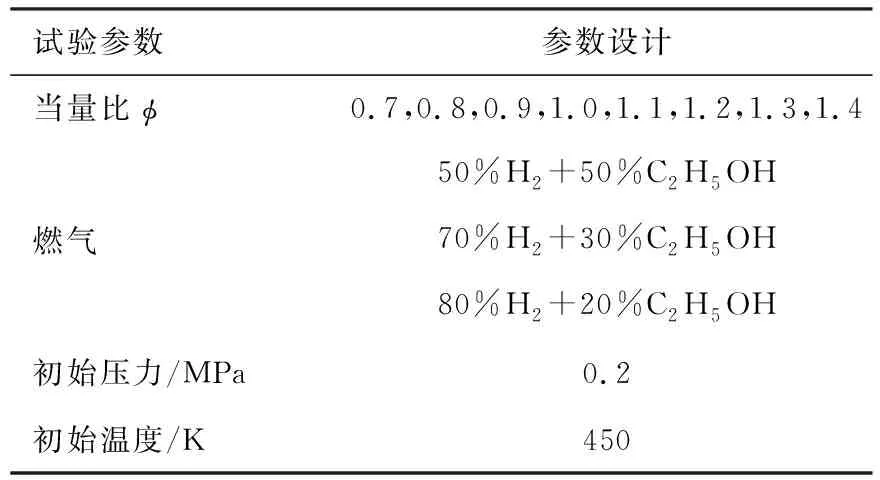
表2 试验的燃气和工况

为了简洁表示,依据氢气与乙醇的体积分数将本试验使用的3组预混燃气分别定义为Xh=50,Xh=70以及Xh=80。

2 层流燃烧特性参数计算

1) 火焰半径

利用图像分析软件获取火焰等效半径[8]Rf:

(2)

式中:Nf为火焰前沿面的像素;Nb为光学窗口的像素;Rb为光学窗口的实际半径。

2) 拉伸火焰传播速度与拉伸率

拉伸火焰传播速度(Sb)由下式计算[9]:

(3)

式中:t为火焰半径Rf对应的时间。

对于球形膨胀火焰,拉伸率α已在参考文献[10]中明确定义:

(4)

式中:A为火焰前沿的面积。

3) Markstein长度

常使用Markstein长度(Lb)来表征火焰对拉伸的敏感程度。Lb为正表示层流燃烧速度随拉伸率的增大而减小,火焰传播过程中火焰前锋面的突起会受到抑制,火焰处在稳定状态;而Lb为负表示火焰的不稳定性增强。Markstein长度可通过线性外推法计算[11]:

(5)

但在实际试验过程中,火焰传播速度的变化是非线性的,Kelley等[12]非线性拟合出计算Markstein长度的更精确的公式:

(6)

无拉伸火焰传播速度计算公式如下:

(7)

式中:ρb和ρu分别为已燃气和未燃气的密度。ρb通过Chemkin中的热平衡模型计算获得,ρu由燃气的初始参数计算。

火焰厚度(δ)和火焰膨胀率(σ)是与流体动力学不稳定性相关的两个主要参数:

(8)

式中:Tb和Tu分别是燃烧的和未燃烧的气体的温度;(dT/dx)max是最大温度梯度。

(9)

σ越小,流体动力学不稳定性越弱。

在假设准稳态和准平面的情况下,利用燃气燃烧过程中的火焰密度变化和无拉伸火焰传播速度[13],层流燃烧速度基于质量守恒定律,使用式(10)计算:

(10)

考虑到火焰厚度的影响,Bradely等[9]提出LBV的另外两种定义,一是um,为燃气的消耗速率,二是umr,为燃烧气体的生成速率,计算公式如下:

(11)

(12)

其中,S为火焰速度因子,其与火焰半径和两区密度比有关[14],计算公式如下:

(13)

其中δL=v/uL,v是未燃气体混合物的运动黏度系数。

3 试验结果与分析

3.1 火焰半径随时间的变化规律

选取φ=0.7、φ=1.0和φ=1.4分别代表贫燃、化学计量比和富燃状态。图3示出Xh分别为50,70和80时在当量比变化下的球形火焰半径随时间的变化规律。随着时间的增加,火焰半径增大,Xh为80时的火焰半径增长速度大于Xh为70和50时。这是因为混合气中氢气比例的提高,会减少燃烧时间。

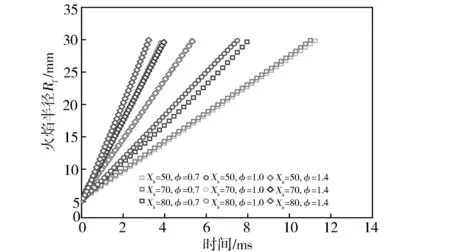
图3 不同比例的混合气在当量比变化下的球形火焰半径变化

3.2 拉伸火焰传播速度与Markstein长度

选择稳定燃烧阶段(即火焰半径选取范围是8～25 mm)的拉伸火焰传播速度来分析火焰稳定性并计算层流燃烧速度。图4示出的是Xh=50的拉伸火焰传播速度随火焰半径变化关系。当Xh=50,φ=0.7时,火焰传播速率基本不随半径变化;当量比为0.8～1.3时,火焰传播速度随火焰半径的增加而增大,而当φ=1.4时变化趋势正好相反。

图4 Xh=50的拉伸火焰传播速度随火焰半径的变化

图5示出贫燃、化学计量比和富燃状态下,拉伸火焰传播速度与火焰半径的变化。φ=1.4时拉伸火焰传播速度大于φ=1和φ=0.7时的拉伸火焰传播速度,这表明提高当量比可以加快火焰传播速度,这与图3结果对应。将图5纵向对比可以发现,化学计量比下,拉伸火焰传播速度与掺氢比之间呈正相关关系。通过扩大氢气在总燃气中的占比,由于氢气燃烧更迅速,会促进燃气的燃烧,进而会提高燃气的拉伸火焰传播速度。

图5 贫燃、化学计量比和富燃状态下,拉伸火焰传播速度与火焰半径变化曲线

图6示出不同当量比和掺氢比下拉伸火焰传播速率与拉伸率的关系。当Xh=50,φ为0.7和1.0时,直线的斜率均为负,对应了正Lb,说明此时火焰稳定;而在φ=1.4时,虽然火焰传播速度最大,但火焰的不稳定性增加,如图6a所示。在化学计量比下,不同掺氢比的预混燃气均呈现为稳定状态,如图6d所示。

图6 不同当量比和掺氢比下拉伸火焰传播速率与拉伸率的关系

图7 无拉伸火焰传播速度随当量比的变化关系

图8示出不同掺氢比下Markstein长度与当量比的关系。可以发现,随着当量比的增加,Lb逐渐减小,在当量比为1.4左右变成负值,火焰的稳定性削弱。这表明,掺氢比和当量比两者都对预混火焰的稳定性有显著影响。

图8 不同掺氢比下Markstein长度与当量比的关系

3.3 层流燃烧速度

不同当量比和掺氢比下,拉伸率对火焰燃烧速度的影响如图9所示。从图中可以看出,随着掺氢量的增加,um与umr的差值在缓慢增大,说明火焰厚度对燃烧速度的影响也在增加,且火焰厚度对燃烧速度产生最明显的影响是在当量比为1.4时。这是由于掺入氢气增加了可燃物浓度和火焰厚度,减小了扩散限制,提高了燃烧速度,并且在当量比为1.4时,燃气达到了最佳配比,使火焰厚度对燃烧速度的影响最为显著。

图9 不同当量比和掺氢比下拉伸火焰燃烧速度随拉伸率的变化

图10示出了在化学计量比、不同掺氢比下拉伸率对燃烧速度的影响。可以看出,对于不同掺氢比的混合气,um和umr都随拉伸率的增加而减小。随着拉伸率的逐渐增加,um和umr的差值逐步扩大,可以看出燃烧速度受到了火焰厚度影响。结合拉伸率的定义可以得出,当拉伸率趋于零时,火焰厚度的影响可以忽略不计,这时无论火焰燃烧速度定义在火焰锋面的哪一侧,它们都应接近于层流燃烧速度uL,即图10中对应为拟合直线在Y轴上的截距。

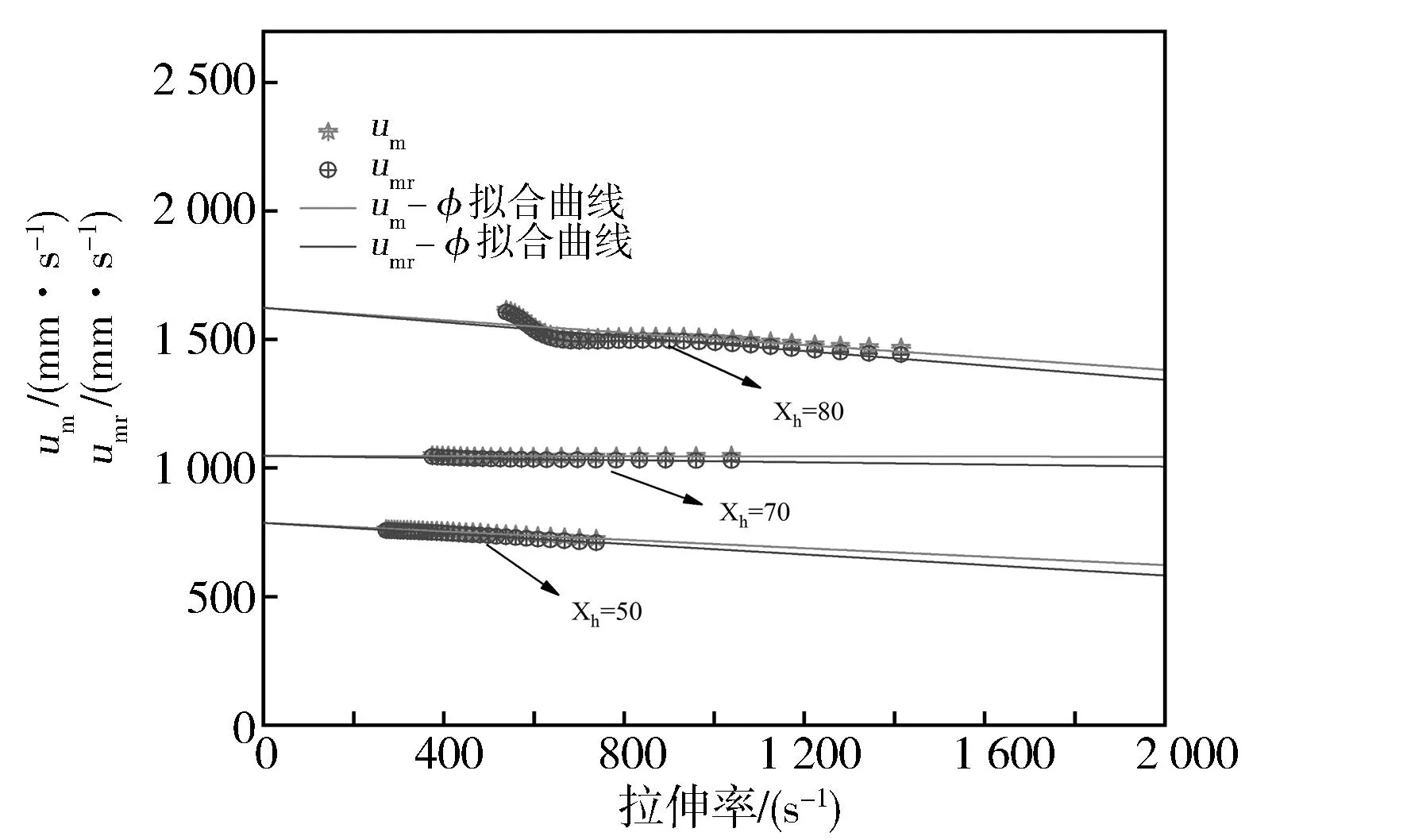
图10 化学计量比下拉伸率对燃烧速度的影响

图11示出氢气-乙醇-空气混合气在不同掺氢比和当量比下的层流燃烧速度。

图11 氢气-乙醇-空气混合气在不同掺氢比和不同当量比下的层流燃烧速度

把LBV拟合成关于当量比的三阶多项式的形式,本研究中LBV的拟合结果为

uL1=2 132.885 64-9 082.528 28φ+12 169.860 08φ2-4 487.261 3φ3,

(14)

uL2=1 766.794 5-7 052.389 11φ+10 076.016 82φ2-3 775.555 33φ3,

(15)

uL3=1 103.046 11-4 374.451 38φ+8 212.322 26φ2-3 423.004 1φ3。

(16)

式中:uL1,uL2,uL3分别对应Xh=50,Xh=70和Xh=80的层流燃烧速度。

对于3组预混燃气,层流燃烧速度随当量比的增加均呈现出先升高后降低的趋势。这是由于在贫燃阶段,随着当量比增加,燃烧会释放更多的能量,使LBV提高;而在富燃阶段,空气逐渐减少,导致反应速率以及燃烧效率降低,进而抑制了预混燃气的LBV,因此,层流燃烧速度在达到峰值后会随着当量比的提高逐渐降低。

将本研究与Z. Han等[14]、Nathan Hinton等[15]、Zhongwei Meng等[16]以及Ziyu Wang等[17]的研究进行了比较,用来印证本试验研究的有效性,结果见图12。发现在相同的初始压力、几乎相同的初始温度下,在LBV增长趋势上,本研究所得结果与4组文献数据近似,可以得出结论,本研究中获得的数据是有效的,具有分析价值。

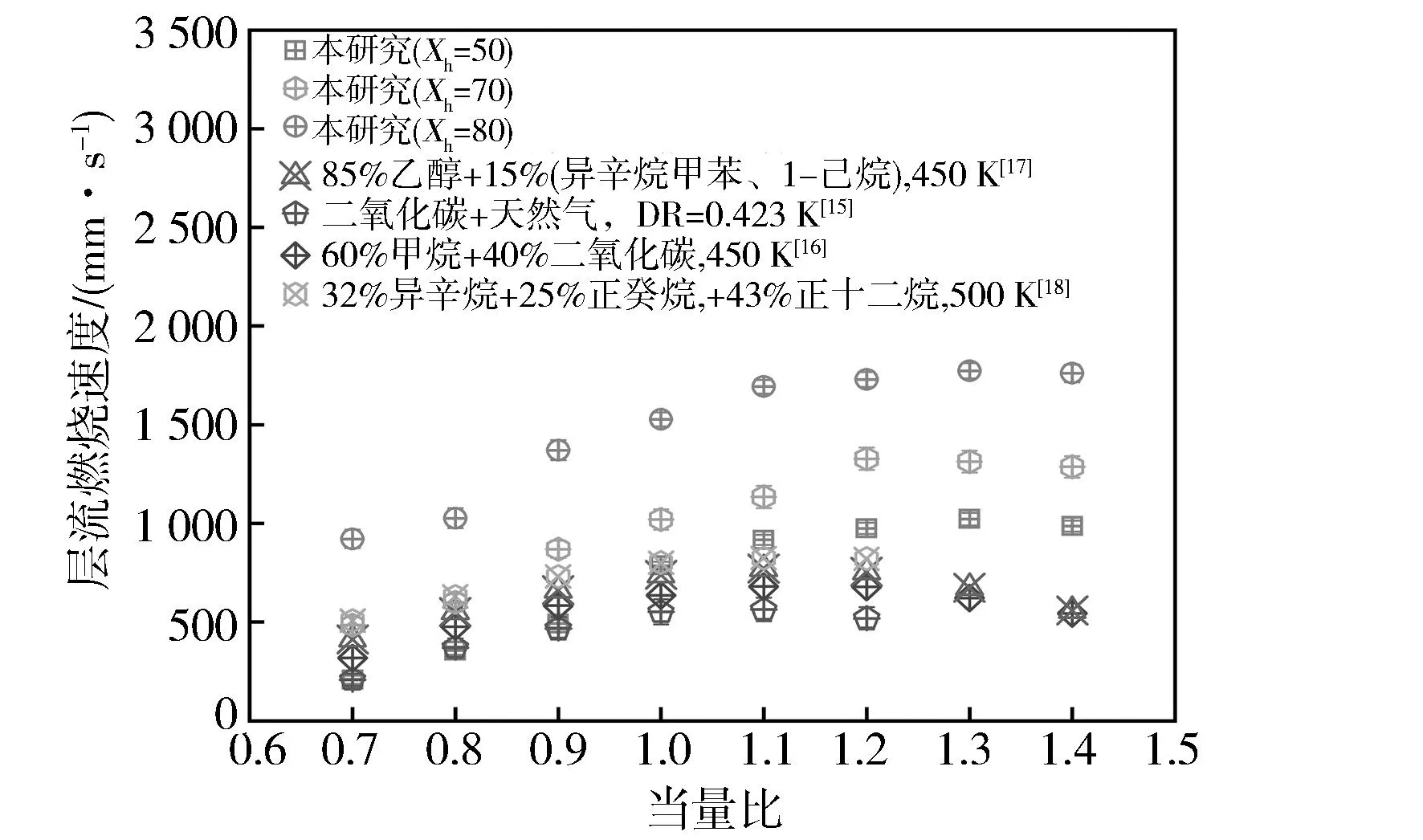
图12 不同燃气的层流燃烧速度对比

层流燃烧速度增长率定义为(uφ=x-umin)/(umax-umin),uφ=x是当量比为x时预混燃气的层流燃烧速度,umax,umin为同一工况下的最大和最小层流燃烧速度。图13示出了初始温度为450 K、初始压力为0.2 MPa时,不同掺氢比下,预混燃气的层流燃烧速度增长率受当量比影响曲线。以掺氢比作拟合可以发现:当φ<1.3时,燃烧速度增长迅速;当φ=1.3时,层流燃烧速度增长率均达最大值,并与最大层流燃烧速度对应;当φ>1.3时,层流燃烧速度增长率呈下降趋势。结果表明:掺氢比、当量比的变化均能影响预混燃气的层流燃烧速度增长速率。将层流燃烧速度增长率进行拟合,得出:

图13 不同掺氢比下层流燃烧速度增长率与当量比的变化关系

(17)

由式(14)至式(17)就可以求出不同掺氢比(Xh为50,70,80)和不同当量比(0.7～1.4)下混合气的近似层流燃烧速度。

4 结论

a) 扩大氢气在总燃气中的占比能加速火焰的传播,但提高燃气中氢气的含量也会削弱火焰的稳定性,随着掺氢比的提高,火焰的不稳定性增强;

b) 随着拉伸率的增大,混合气消耗速率与产物生成速率的差值逐渐扩大,当拉伸率趋于0时,um和umr都趋于LBV;层流燃烧速度增长率最大值出现在当量比为1.3时,这与最大层流燃烧速度相对应;

c) 本研究中3种预混燃气的LBV均呈现出先升高后降低的趋势,其峰值(1 022.11 mm/s,1 313.275 mm/s,1 773.129 mm/s)均出现在当量比为1.3时。