断层破碎带区域贯通施工的富水隧道力学特性分析

吴 波, 刘兆春, 刘 聪

东华理工大学 土木与建筑工程学院, 江西 南昌 330013

0 引言

随着经济快速发展, 交通运输网的完善, 隧道工程所占比重不断扩大, 中国成为世界上隧道工程最多、 最复杂、 发展最快的国家[1]。 隧道发挥着缩短运输距离, 提高运输效率的作用。 对于地质环境复杂、富水地区的隧道建设, 通常面临着渗水、 围岩岩性差易坍塌等难题。 隧道贯通时, 贯通段的支护材料强度尚处于上升阶段, 易引起隧道贯通段塌方, 给隧道工程施工带来极大的安全隐患[2]。 隧道相向施工临近贯通时, 随着两端掌子面的不断靠近, 隧道开挖产生的扰动区将会相互叠加, 围岩应力及变形较单向施工时更复杂[3]。 贯通段作为隧道工程灾害的易发地段, 因此有必要研究隧道贯通力学行为以提出确保安全的贯通方案与技术措施[4]。 隧道贯通施工本就是一个难点[5], 对于隧道贯通段的选址, 其贯通段往往会避开在围岩较差的地段而选择在围岩岩性相对较好的地段, 但受线路走向限制, 隧道常需穿越如断层构造破碎带等复杂地质环境[6]。 破碎带内的岩体强度极差,且存在地下水时, 破碎带会给地下水提供良好的渗流路径, 地下水渗流则会影响隧道围岩的应力场和位移场[7,8], 也会对掌子面的平衡造成扰动, 引发掌子面产生失稳破坏[9], 施工时容易发生涌水突泥事故。 分析隧道在破碎带贯通时围岩的力学特征对研究隧道在复杂地质条件下施工可能引起的灾害的时机及对灾害的预防具有重要意义。

对于隧道穿越破碎带的研究, 大多学者是基于数值仿真模拟从不同的角度进行的, 陈泽龙等[10]通过分析隧道开挖过程中断层带和非断层带塑性区的贯通发展情况得出了隧道突水突泥的临界时机, 安永林等[11]基于强度折减有限元法论证了掌子面在不同的开挖进尺下的稳定性, 高乐等[12]通过建立数值模拟模型分析了富水断层破碎带隧道施工围岩应力重分布和位移变化情况, 为隧道涌水高危段落的划分提供了参考。 李廷春等[13]建立孔隙渗流模型对破碎岩体的渗流特点进行研究, 观察孔隙水压力分析渗流场变化总结了隧道断层破碎带的突水塌陷机理。 但其研究大多数是基于围岩在固定含水量工况下穿越破碎带的基础上进行的, 地下水渗流对隧道开挖过程中围岩的影响是随着水头高度的变化下而发生变化的, 且对于岩体破碎地段多的隧址区, 隧道在破碎带贯通的研究较少, 具有研究意义。 因此, 本文选取在破碎带作为隧道的贯通段, 并采用数值模拟方法分析在不同水头高度下施工时隧道围岩的竖向位移、 最大主应力、 塑性区、 孔隙水压力、 掌子面挤出变形的演变特征, 为类似工程提供一些参考。

1 渗流—应力场耦合

隧道施工过程中的流固耦合指的是隧道围岩岩土介质渗流与应力耦合关系, 岩土体的流—固耦合是水体流动和介质变形相互作用、 相互影响的结果[14]。隧道围岩是由固体骨架与孔隙和水组成多孔介质, 其存在裂隙节理, 受地下水流影响, 富含裂隙水。 本文在数值模型区域内假定隧道周围岩土介质的骨架为均质弹塑性体, 孔隙水渗流服从达西定律。 达西定律表达式为:

式中,Q表示通过砂柱的水的流量,A表示过水断面的面积,K为渗透系数,h1、h2为上下水头高度,L为渗流长度。

研究弹塑性体的流固耦合即考虑岩土体变形与孔隙水压力之间的耦合作用, 采用基于Biot[15]固结理论优化后的多孔介质的有效应力原理, 构建等效连续介质的渗流场—应力场模型:

式中,ϕ为孔隙度;P为孔隙流体的压力;为固体颗之粒间的应力;σij为岩土介质中的总应力张量;Tijkl为裂隙岩体的四阶对称弹性柔度模量;P为岩土介质的地下水渗透压力;σeij为岩土介质中的有效应力张量;Kij为渗透系数张量;Aij为裂隙几何张量; 为有效应力张量σij的函数。

2 工程概况

莆炎高速公路文笔山1# 隧道右隧起止里程K218+565～K+240, 左隧起止里程ZK218+565 ～ZK223+240, 总长4 675 m, 为双线分离式隧道, 隧址范围属于中低山地貌, 地面高程600 ～1 320 m, 最大埋深640 m。 隧道穿越地层主要为第四系残积层砂质黏性土, 下覆中风化砂岩、 碎块状强风化砂岩, 侵入混合花岗岩。 受侵入挤压影响, 隧道穿越多处岩体破碎-极破碎的侵入破碎带和原岩为中风化花岗斑岩, 局部挤压破碎呈角砾状, 岩质松软的断层破碎带, 部分工程地质纵断面如图1 所示。 根据地质调查报告资料显示, 混合花岗岩碎块状强风化岩体破碎, 节理、 裂隙十分发育, 富水条件较好。 隧道建设地区全年雨季达8 个月, 雨量多, 强度大, 隧道施工过程中易发生地质灾害。

图1 工程地质纵断面图Fig.1 Longitudinal section of engineering geology

3 数值模拟

3.1 模拟方案和工况

选取ZK219+835 ～ZK219+995 侵入破碎带段作为数值模拟的岩体模型, 探讨隧道在围岩存在不同高度的水头条件下双向开挖至破碎带贯通时围岩的演变情况。 该数值模型采用ABAQUS 进行创建, 建立如图2所示的三维隧道开挖模型, 隧洞断面宽16.75 m, 高9.94 m, 考虑到隧道开挖过程中产生的空间效应, 隧洞至模型水平边界尺寸不低于3 倍洞径, 模型纵向取70 m, 宽取120 m, 高120 m, 隧洞顶部距模型顶部表面70 m。

图2 数值模拟模型Fig.2 Numerical simulation model

对模型四周和底面进行法向位移约束, 孔隙水压力为静水压力, 取隧道开挖面及水位面为透水边界。隧道围岩采用摩尔—库伦弹塑性本构模型, 为简化模型计算步骤, 更直观的得出隧道施工过程中周边围岩力学特性的变化, 隧道施工采用上下台阶法双向同时掘进模拟开挖[16], 两侧单向分别开挖35 m 至模型中心贯通。 同时为了论证进尺对模拟结果的影响以及模拟结果更为精准, 隧道前15 m 开挖台阶长度为3 m,之后20 m 开挖台阶长度为1 m, 见图3。 隧道施工只考虑初期支护的施做, 厚度为25 cm, 不考虑二次衬砌, 初期支护不考虑渗水且在每一开挖循环完成后立即进行, 模型顶面采用施加均布荷载模拟隧道实际埋深上部覆土压力。

图3 隧道开挖示意图Fig.3 Schematic diagram of tunnel excavation

隧道开挖模型计算参数根据《莆炎高速公路工程地质详勘报告》 选取, 如表1 所示。 为观察裂隙水在隧道施工过程中对隧洞周边围岩的影响, 分别在干燥(无水), 水头高度距离隧洞顶部0 m、 10 m、 20 m、30 m、 40 m 6 种工况下进行数值模拟分析, 模型整体共计35 350 个单元, 40 035 个结点, 总共设立79 个分析步, 从第1 个分析步开始模拟隧道进行双向掘进直至第79 个分析步完成隧道的贯通和整个模型隧道初期支护的形成。

表1 模型计算参数Table 1 Model calculation parameters

为准确的获取数值模型模拟计算得出各工况下的数据, 根据隧道项目施工中实际布置的断面监测点的位置及数值模型中受影响较为明显的部位综合考虑, 在数值模型隧道断面上设置了3 处特征点, 见图4。

图4 隧道断面特征点Fig.4 Characteristic points of tunnel section

3.2 数值模拟结果

3.2.1 竖向位移

隧道掘进过程中会对隧洞周边围岩造成不同程度的位移, 其中对隧道拱顶和拱底围岩的位移影响较为明显, 通过数值模拟得出隧洞周边围岩竖向位移情况如图5 所示。

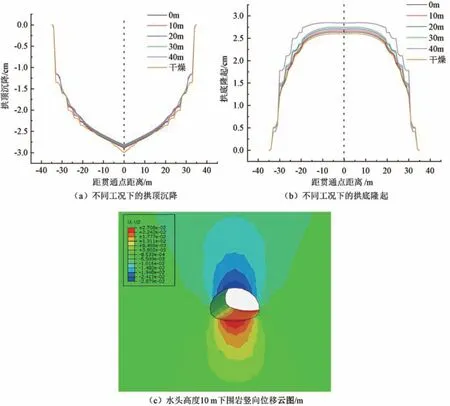
图5 隧道围岩竖向位移云图Fig.5 Vertical displacement cloud map of tunnel surrounding rock

以水头高度在隧洞顶部10 m 处工况为例, 见图5(c), 围岩竖直位移的影响范围在拱底和拱顶呈灯泡状, 拱顶最大沉降2.87 cm, 拱底最大隆起2.7 cm,在隧道洞径宽度, 离拱顶垂直高度25 m, 离拱底高度20 m 范围内有较大影响。 由图5 (a) 和5 (b) 可知, 与围岩富水相比, 在围岩干燥得情况下拱顶的沉降较大、 拱底的隆起均比较小。 在围岩富水工况下,随着水头高度的不断提升, 拱顶沉降有所减小, 拱底因水压力的增加, 隆起有所增大。 通过数值模型导出的结果得出, 其趋势均为前20 个开挖步(17 m), 位移值急速增加, 在20 步之后逐渐趋于平稳。 数值位移图的增长速率与增长大小趋势符合围岩中含水的位移实际情况。 对比分析各工况下的总位移值, 水头高度每增加10 m, 拱顶沉降平均减少0.2 mm, 拱底隆起平均增加0.3 mm。 将数值模拟得出得拱顶沉降结果与项目实测数据进行对比, 以验证模型的可靠性,如图6 所示。

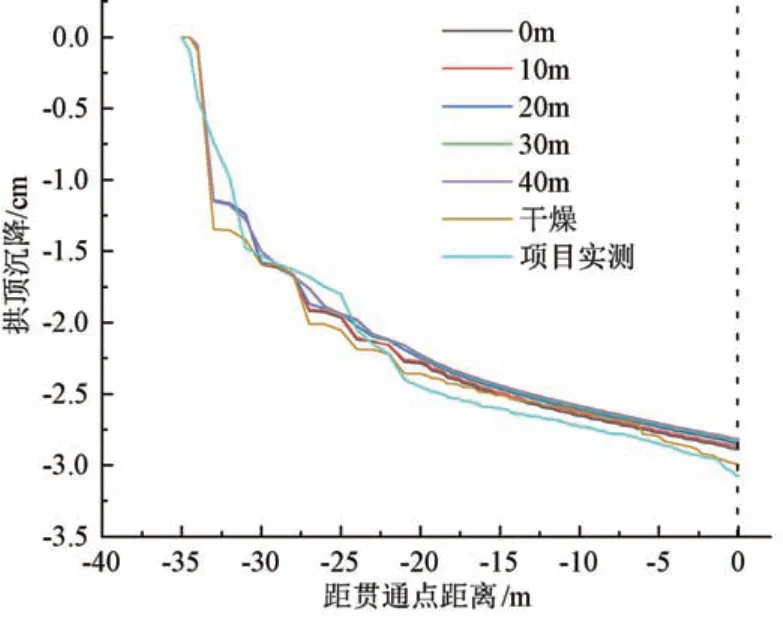
图6 模拟结果与实测数据拱顶沉降对比Fig.6 Comparison between the simulation results and the measured data of arch roof settlement

隧道开挖至破碎带时正直梅雨季节, 隧道围岩含水量较大, 由图可知项目实测数据与模拟结果趋势大致吻合, 其沉降值略大于6 种模拟工况, 存在细微误差, 原因主要是现场实际围岩裂隙程度往往更大, 地质情况和破碎情况更加复杂多方面造成的。 但数值模拟得出的结果依旧可以验证围岩位移趋势的正确性和数值的准确性, 证明数值模拟结果是可靠的。

3.2.2 最大主应力

应力应变水平可以直观的得出隧道围岩荷载的强度变化规律[17,18]。 隧道开挖后, 围岩应力重分布如图7 (a)、 7 (b) 所示, 干燥及富水工况下, 应力场分布情况基本一致, 均呈现随着隧道开挖距离的不断增加围岩应力水平方向范围不断向隧洞方向收缩, 纵向不断向隧道开挖方向集中, 围岩的最大主应力最终集中在隧道两侧拱腰处, 大体呈对称状态。

图7 最大主应力Fig.7 Maximum principal stress

因整体隧道模型的模拟结果大体呈YZ 面对称,故选取隧道一侧进行结果分析, 后同。 如图7 (c)所示, 通过对6 种工况下隧道拱腰应力集中区最大主应力对比, 结果见图7 (d)。 以隧洞左侧拱腰处为例, 隧道施工进程中, 隧道拱腰处的最大主应力随着双向掘进距贯通点的距离不断减少, 呈现先增大后减小的趋势, 在贯通点处达到最小值。 在不同水头高度的模拟情况下, 随着水头高度的增加, 最大主应力减小。

3.2.3 塑性区域

隧道开挖过程中, 围岩应力场重分布, 超过弹性屈服阶段进入塑性屈服阶段, 产生塑性区域。 在同一埋深下, 随着围岩破碎程度的增加, 围岩的受拉区和塑性变形区逐渐从拱顶、 底向边墙转移[19], 双向开挖快接近贯通点时, 两掌子面之间围岩产生的塑性区域将会形成贯通, 受地下水软化作用明显, 该区域岩体裂隙发育扩大并相互连通, 加剧地下水的流失和渗流作用[20], 极易造成突涌水灾害。 塑性区域的贯通范围和大小对探究围岩的稳定性和支护的时机有着重要决定性作用, 研究塑性区贯通的时机对于预防隧道的坍塌有着重要作用。 6 种工况下塑性区分布如图8所示。

图8 不同工况塑性区贯通云图Fig.8 Penetrating cloud map of plastic zone under different working conditions

对不同工况下的塑性区域恰好贯通时的模拟结果进行对比, 如表2 所示。 随着水头高度的增加, 围岩产生塑性屈服的范围扩大, 塑性区的贯通距离增大,掌子面最大等效塑性应变越大。 可因此来判断对隧洞进行支护的安全距离, 此刻应及时停止其中一方向的开挖, 换以单方向继续掘进至隧道贯通, 防止双向隧道开挖导致应力场扰动叠加, 避免隧道突涌水造成的周边围岩及掌子面失稳坍塌风险。

表2 不同工况塑性区域对比Table 2 Comparison of plastic regions under different working conditions

同时对6 种工况下隧道两侧的拱腰处塑性区的等效塑性应变变化情况进行对比, 结果如图9 所示, 从开挖至贯通的过程中, 等效塑性应变总体呈现先增大后减小再增大直至贯通点时达到最大值。 岩体含水时, 使围岩的黏聚力降低, 干燥工况下拱腰处的等效塑性应值变明显低于围岩含水工况, 随着水头高度的增长, 等效塑性应变值也随之略有提升。

图9 不同工况下拱腰处等腰塑性应变对比Fig.9 Comparison of isosceles plastic strains at the arch waist under different working conditions

3.2.4 孔隙水压力

岩体中水头高度的不同影响着围岩中孔隙水压力的大小, 数值模型中孔隙水压力为静水压力, 随着水头高度平均每增长1 m 增加0.01 MPa, 开挖时, 隧洞周围的孔隙水压力服从该规律, 通过数值模拟可以得到隧道在开挖过程中周边围岩孔隙水压力的演变情况。 以30 m 水头高度工况为例, 隧道两边掌子面距离12 m, 即隧道双向掘进至塑性区贯通时, 如图10所示。 隧道的开挖面周围产生负的孔隙压力, 此时隧道周边围岩及掌子面中的裂隙水涌入隧洞内, 涌水速度矢量图见图11。 针对不同程度突涌水, 在隧道施工中需采取特定的支护措施进行防治, 采取“短开挖,强支护”。

图10 隧道开挖孔隙压力云图(Pa)Fig.10 Cloud map of pore pressure in tunnel excavation

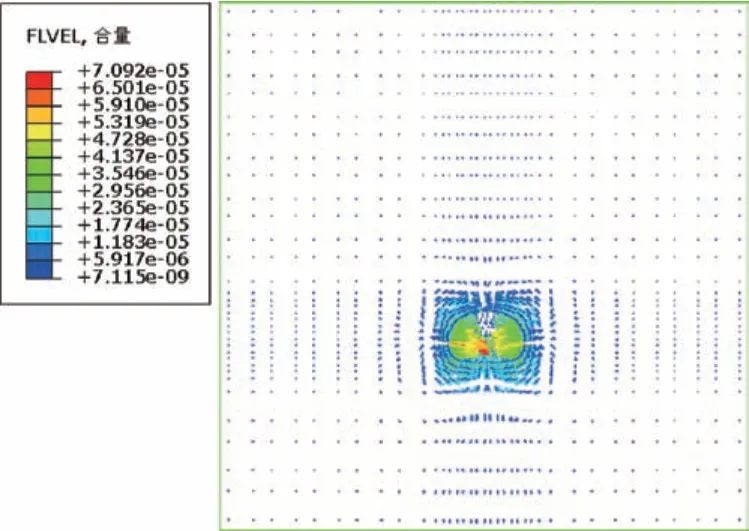
图11 隧道涌水速率矢量图(m/s)Fig.11 Vector diagram of tunnel water inflow rate

如图12 所示, 施工过程中, 隧道的开挖面没有施做初期支护, 原有稳定的渗流场改变, 隧洞周边孔隙水压力严重下降。 随着隧道不断向前开挖, 由于之前开挖段隧洞初期支护的及时封闭, 隧洞周围孔隙压力趋于稳定。

图12 孔隙压力变化云图(Pa)Fig.12 Cloud map of pore pressure change

同时对比了隧道开挖过程中拱腰处、 拱底处、 拱顶处孔隙水压力的变化情况, 见图13, 初始孔隙水压力随着水头高度的增加而增加, 符合静水压力趋势。结果显示隧道的拱腰处孔隙水压力随着隧道开挖不断深入孔隙水压力呈现不断增加的趋势, 且开挖至距离贯通点8 m 左右急剧减小, 水头高度的不断增加, 孔隙水压力的变化拐点越来越提前, 拐点由水头高度0 m 时距离贯通点7 m 提前至水头高度40 m 时距离贯通点8 m; 拱底处孔隙水压力随着隧道开挖不断深入呈现减小趋势, 且开挖至距离贯通点3 m 左右小幅度增加, 水头高度的不断增加, 孔隙水压力的变化拐点距离贯通点越近, 由水头高度0 m 时的4 m 减少至水头高度40 m 时的3 m; 拱顶处孔隙水压力则随着隧道开挖直至贯通点始终呈减小趋势。

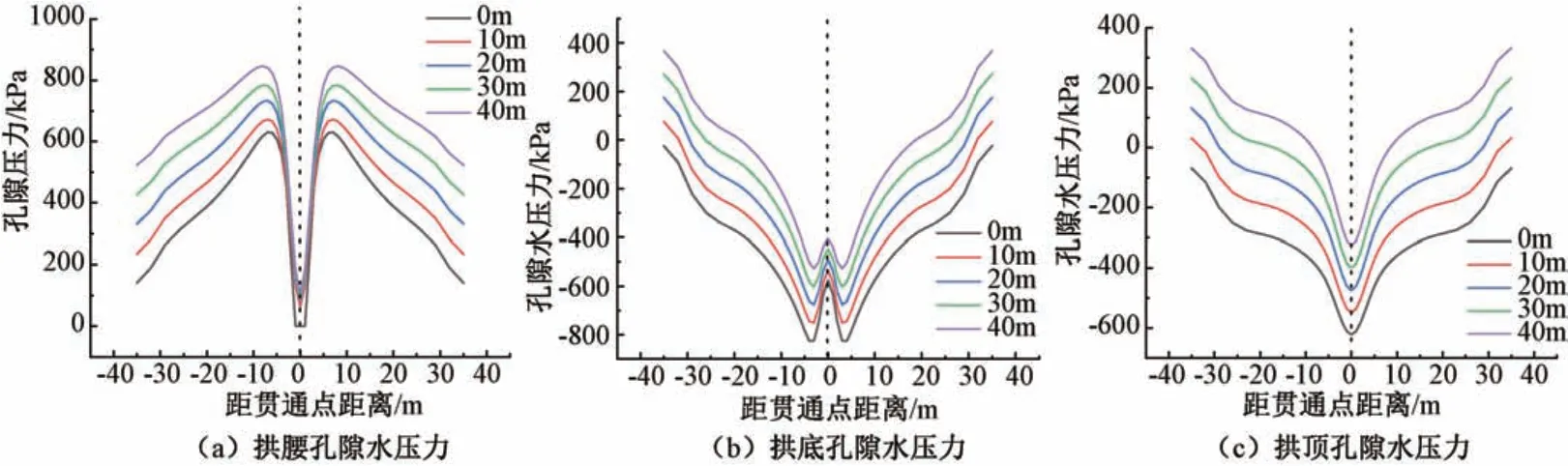
图13 不同水头高度下孔隙水压力对比Fig.13 Comparison of pore water pressures under different water head heights

结果表明, 由于围岩破碎, 孔隙率较大, 地下水会顺着孔隙通道深入隧道内部, 表现为隧道周边围岩的孔隙水压力迅速减小, 且隧道内突涌水风险及涌水量在贯通区最大, 随距贯通点距离增大而减小; 另一方面, 在支护结构施作完成后, 由于支护结构的防水作用, 会使得周边围岩的孔隙水压力逐步恢复至开挖前的水平。

3.2.5 掌子面挤出变形

在隧道围岩富水环境下, 掌子面的变形对隧道的稳定性有着关键性影响, 掌子面在施工过程中受到洞周和掌子面后方岩体向洞内方向的应力挤压产生向隧道纵向的突出变形。 通过模拟隧道开挖得出上下台阶法施工过程中掌子的面变形情况, 以水头高度40 m工况隧道开至双向塑性区贯通时掌子面挤出变形为例, 见图14。 由图14 (a) 可见掌子面的挤出变形最大值集中在上下台阶的分界线中心位置, 不断向隧洞周围减少。 上台阶的最大挤出变形发生在台阶的中下部, 下台阶的最大挤出变形发生在台阶的中上部。 由图14 (b) 可见掌子面变形范围在掌子面后方呈半圆状, 挤出变形量以掌子面上下台阶分界线中心位置沿隧道纵向呈圆弧状逐渐减小。

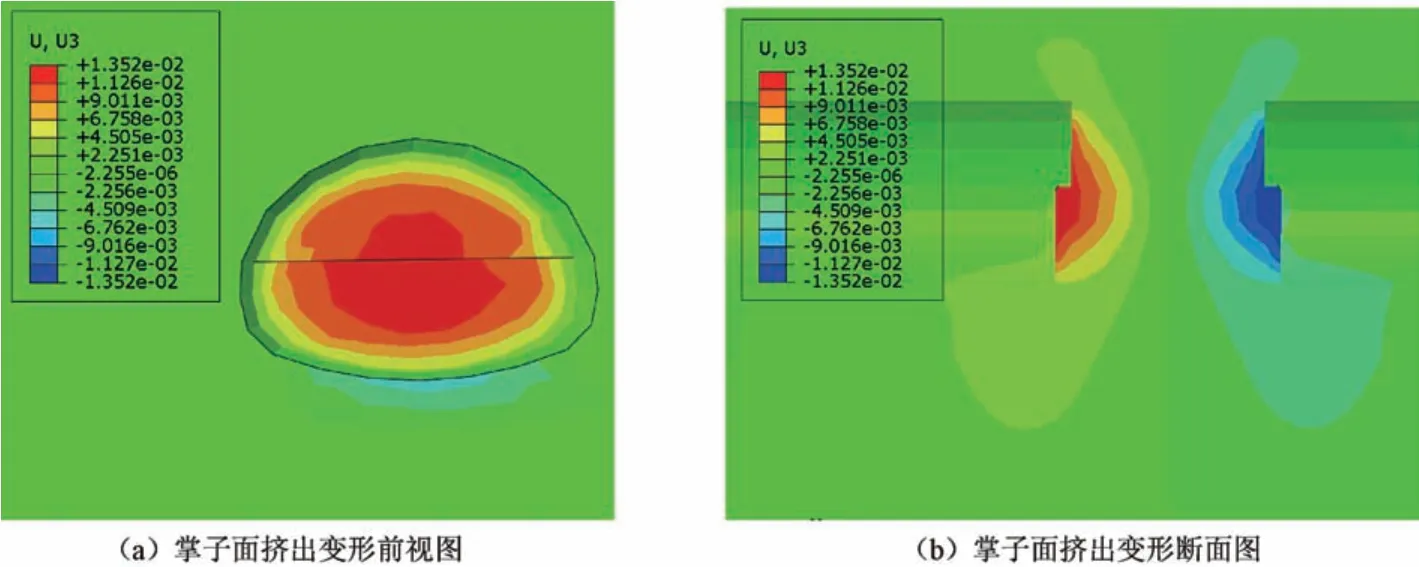
图14 水头高度40 m 掌子面变形云图(m)Fig.14 Cloud map of deformation of the face at a water head height of 40 m

对岩体干燥和不同水头高度的6 种工况下隧道上下台阶掌子面随开挖距离演变的挤出变形数据整理后进行对比, 见图15。 开挖面与贯通区距离越大, 隧道掌子面挤出变形越小, 说明贯通区坍塌风险极高。 在贯通位置处, 挤出变形迅速降低, 是由于该部分原有挤出变形较大的岩体被挖除所致,

图15 掌子面上下台阶隧开挖距离最大变形图Fig.15 The maximum deformation diagram of the excavation distance of the upper and lower step tunnels on the face

挤出变形在隧道开挖由3 m 进尺至15 m 处转为1 m 进尺时有一个很明显的衰减趋势, 表明隧道开挖进尺对掌子面的挤出变形稳定性有一定影响, 进尺的减小会提升掌子面的稳定性。 通过对比, 掌子面挤出变形随水头高度每增加10 m 平均增大0.77 mm, 这表明, 地下水的存在, 会显著增大掌子面挤出变形,增加贯通区失稳风险。

由此可见, 地下水不仅会增大贯通区的突涌水量, 还会显著增大隧道贯通区的挤出变形, 提高失稳风险, 因此因尽量避免在富水区域进行隧道贯通作业。

4 结论

本文依托福建莆炎高速公路文笔山1#隧道工程,基于渗流场—应力场耦合原理建立了破碎带深埋隧道三维数值仿真模型, 研究了富水破碎带中贯通隧道的力学特性, 主要结论如下:

1) 在拱腰围岩处的最大主应力、 拱顶沉降与拱底隆起分别随着水头高度增加呈减小和增大趋势; 塑性区随着水头高度的增加, 贯通距离增大, 掌子面挤出变形增大, 且开挖进尺的减小, 掌子面的稳定性越高。 隧道在开挖过程中孔隙压力向隧洞周围集中, 且隧道开挖面在初期支护及时封闭后孔隙水压力趋于稳定。

2) 建立了隧道在破碎带双向掘进贯通的流固耦合仿真模型, 围岩破碎, 孔隙率较大, 地下水会顺着孔隙通道深入隧道内部, 表现为隧道周边围岩的孔隙水压力迅速减小, 且隧道内突涌水风险及涌水量在贯通区最大, 随距贯通点距离增大而减小。

3) 水头高度每增加10 m, 掌子面挤出变形约增大0.77 mm, 地下水不仅会增大贯通区的突涌水量,还会显著增大隧道贯通区的挤出变形, 提高失稳风险, 隧道应尽量避免在富水区域贯通。