深埋底抽巷炮掘水间隔装药结构与炮眼布置优化

刘少伟，隋纪胜，贾后省，付孟雄，于 涛，姚丙傲

(1.河南理工大学 能源科学与工程学院，河南 焦作 454000；2.煤炭安全生产与清洁高效利用省部共建协同创新中心，河南 焦作 454000；3.河南省新郑煤电有限公司，河南 新郑 451100)

钻爆法作为破岩成巷(隧)的主要技术手段之一，具有施工成本低、效率高的特点，适用于低瓦斯矿井巷道及隧道掘进[1]。随着我国煤炭资源开采逐步向深部发展，巷道埋深增加，围岩应力增大，导致炸药单耗增加、成巷(隧)效率降低，而巷道掘进的施工进度是制约井下开采效率的因素之一[2]。如何实现快速掘进并保证施工进度及施工人员的安全，成为现阶段亟需解决的难题。因此，对钻爆中炮孔的布置、装药结构的设计提出了更高要求。

如何提高炮孔利用率是国内外众多学者研究的主要方向。谢理想[3]等采用数值模拟的方法对地应力与应力波传播进行了分析，研究结果得出地应力对应力波产生的压力荷载具有抵制作用，使得岩体受压力荷载作用产生的损伤范围受到影响；胡建华[4]等利用CAD和LS-DYNA数值模拟软件，构建了爆破精细化网格模型，认为应力波相互叠加作用是影响掏槽腔体成型的关键；龚敏[5]等运用LSDYNA3D进行掏槽参数优化研究，对炮孔的布置形式进行了优化，模拟结果得出当炮孔中存在空孔时，可使掏槽效率提高30%以上；李启月[6]等运用LS-DYNA对不同直径的空孔在爆破时的动态破碎过程进行了模拟，得出了直孔掏槽的应力分布规律；李延龙[7]等对水炮泥堵塞作用运动机理进行研究，并获得了炮泥在孔内的运动规律；杨仁树[8-9]等提出超深掏槽孔掏槽爆破技术用以提高炮孔利用率以及基于炮孔长度优化的问题，证明了存在最优掏槽孔超深系数η可使炮眼利用率达到最高；Yi[10]等探讨了炮孔间微差起爆时应力波之间的相互影响；戴俊[11]等利用ANSYS/LS-DYNA 数值模拟双炮孔爆破裂纹扩展过程，得到了孔间裂缝的合理间距为400～700 mm；宗琦[12-15]等先后对水垫层装药对爆破效果的提升作用、炮孔水耦合装药爆破对孔壁产生冲击压力、炮孔不同的装药结构对爆破能量影响以及水介质不耦合装药结构爆破后对岩石的破坏范围等方面做了大量研究；刘永胜[16]等对爆炸振动场和爆炸应力场进行研究，分析了岩体中缺陷处填充空气或水对爆炸应力场的影响；杨建华[17]等针对深埋圆形隧洞爆破开挖过程，分析了不同掏槽方式对开挖面地应力瞬态卸荷诱发围岩振动的力学特性，从掏槽方式选择、孔网参数布置、起爆网路优化的角度探讨了诱发振动的控制方法；郑祥滨[18]等对单螺旋空孔直眼掏槽的爆炸应力波传播规律与成腔过程进行了数值模拟研究，发现爆破效果与掏槽孔至空孔的距离相关；杨国梁[19]等对复式掏槽爆破进行了分析，发现复式掏槽爆破更有利于孔底岩石向自由面抛出；单仁亮[20]等对巷道掏槽爆破的作用机理进行研究，提出了应力应变特性和岩石性质对掏槽爆破效果的影响；钟明寿[21]等根据爆炸力学的相关理论建立起耦合装药、不同耦合介质(包括水、空气和泥土)装药条件下炮孔壁处爆炸载荷和透射波比能量的计算方法。

钻爆法适用范围广泛，所以在未来很长一段时间内将作为巷道掘进的主流工艺[22]，而目前大部分学者都是针对炮孔的布置形式进行研究，鲜有对装药结构的研究。文章以赵家寨矿岩巷钻爆法施工为背景，提出水间隔柱状不耦合装药结构，旨在为类似岩巷掘进提供可参考的施工方案。

1 底抽巷掘进面概况及存在问题

赵家寨矿14206工作面主采二1煤，煤层埋深约400 m。底抽巷沿灰岩掘进，设计断面为直墙半圆拱形，尺寸为5.1 m×3.6 m，净面积15.8 m2，设计长度1 036.2 m，灰岩的坚固性系数为7。因巷道底板为砂质泥岩与砂岩互层，采用综掘机沿巷道掘进时，掘进段大量用水会导致巷道底板遇水泥化，不利于现场施工，因此采用钻爆法掘进，巷道围岩层位关系及掘进断面如图1所示。

图1 巷道围岩层位关系及掘进断面Fig.1 Layer relationship and excavation cross-section of surrounding rock in tunnels

现场实际调研发现，循环进尺短的主要原因为：掏槽孔和崩落孔的间距超过了药柱的有效破碎半径，导致炮孔之间未完成切割，无法为后续爆破提供新的自由面，造成整体进尺较短，循环进尺为1.5 m，炮孔利用率为75%，且掘进面超欠挖现象较严重。因此，需对14206工作面的底抽巷围岩爆破参数和装药结构进行优化。

2 水间隔装药结构及爆破效果分析

2.1 岩石爆破破碎机理

炸药在岩体中爆破时，爆炸瞬间产生爆生气体和爆生产物使炮孔周围岩石破碎，形成微小颗粒和初始裂隙。冲击波在传播过程中衰减成应力波，在孔壁的切向产生拉应力，形成径向破裂，当径向压缩应力波传播至自由面时，反射形成拉伸波，若反射拉应力大于岩石的抗拉强度，则会引起岩石进一步破裂，包括初始裂隙的扩展和二次裂隙的形成[23]。爆生气体的膨胀、挤压、尖劈作用促使裂隙发生延伸和扩张，形成岩石碎块。炸药爆炸冲击围岩过程如图2所示。

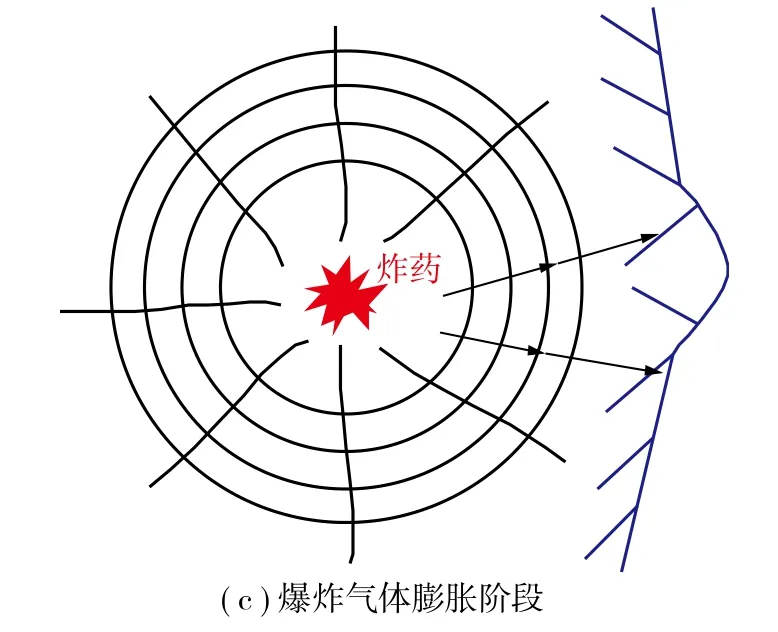
图2 炸药爆炸冲击围岩过程Fig.2 Process of explosive impact on surrounding rock

2.2 单孔爆破计算模型构建及装药结构方案

为了提高岩巷的成巷速度，采用数值模拟水间隔柱状不耦合装药(以下简称水间隔装药)条件下，炸药爆炸形成的有效破碎半径和孔底的破碎状态，以确定最优的炮孔间距和装药结构。

由文献[24]可知，与空气间隔装药相比，水间隔装药应力衰减慢，压力作用时间长，炮孔透射比能量大，可提高爆炸的能量利用率。因此，笔者仅对水间隔条件下岩石破碎效应进行分析。

模拟采用非线性动力有限元软件LS-DYNA，计算模型如图3(a)所示，建立四分之一模型，镜像得到全模型。四分之一模型尺寸为1 m×1 m×3 m，采用solid164实体单元进行网格划分。为保证模拟结果的准确性，岩石、空气、炸药均采用映射网格划分，网格尺寸为1 cm，计算时长1 ms。不同工况时模型尺寸相同，炸药、空气和水均采用初始体积分数法设置，采用动力松弛法设置10 MPa应力，计算时间步与模型最小网格匹配。模型边界被限制在XOY平面上，并被定义为无反射边界模拟波在无限岩体内传播。炮孔直径为38 mm，炸药尺寸为ϕ35 mm×300 mm，选用矿用乳化炸药，炸药密度为1.0 g/cm3，装药方案见表1。

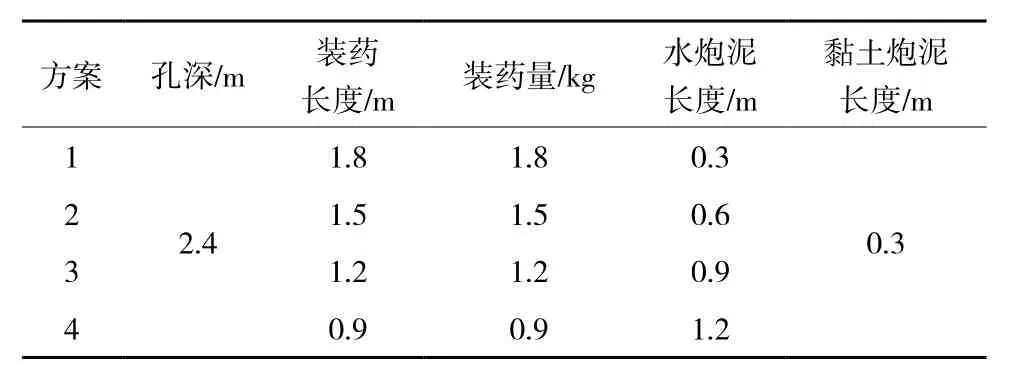
表1 装药方案Table 1 Charging scheme

在距炮孔口0.35 m和孔底0.35 m及岩石中部0.8，1.6 m处分别选取4个测点(Ⅰ，Ⅱ，Ⅲ，Ⅳ)作为分 析对象，测点位置如图3(b)所示。

2.3 模型材料及本构方程

炸药采用MAT_HIGH_EXPLOSIVE_BURN 模型，炸药状态方程采用EOS_JWL方程描述[25]。

式中，P1为爆炸产生的压力；V为相对体积，即当压力为P1时的体积与初始体积的比值；E0为炸药的初始比内能；A，B，R1，R2，ω为参数，由试验确定。

炸药状态方程的主要参数为：V= 1.0 g/cm3，E0= 4.192 GPa，A= 214.4 GPa，B= 0.812 GPa，R1= 4.2，R2=0.9，ω= 0.15。炸药的材料参数为：密度ρ1＝1.0 g/cm3，爆速D＝0.4 cm/μs，单位体积爆轰能E＝4.192 GPa。

空气采用MAT_NULL材料模型，状态方程采用EOS_LINEAR_POLYNOMIAL方程描述[26]。

式中，P2为空气压力；E2为初始单位体积内能；C0～C6为与气体性质有关的常数，其中C0=C1=C2=C3=C6= 0，C4=C5=0.4；μ=ρ/ρ0- 1，其中，ρ，ρ0分别为当前气体密度和初始时刻密度。

空气状态方程及材料参数值见表2。

表2 空气状态方程及材料参数值Table 2 Air state equation and material parameter values

通过实验室试验对现场取样的岩石进行参数标定，岩石材料采用RHT模型，因为混凝土和岩石都具有应变硬化、损伤软化和应变率效应等特性，所以岩石的部分参数可采用RHT混凝土的本构模型来描述岩石在冲击动载下的损伤行为[27]，岩石材料参数见表3。

表3 岩石主要力学参数Table 3 Main mechanical parameters of rock

2.4 爆破动态损伤特征

为观察到不同方案爆破后岩石的动态破碎特征，采用数值化提取技术对岩石的损伤演化过程进行分析，不同装药结构岩石损伤演化结果如图4所示。

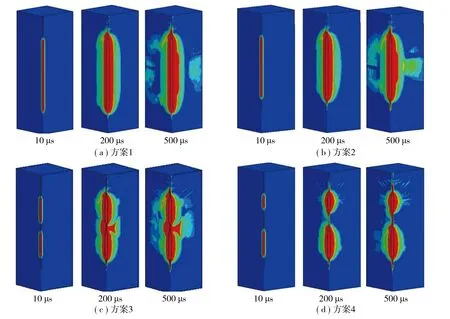
图4 4个方案在不同时步的岩石损伤演化Fig.4 Rock damage evolution of four schemes at different time steps

由图4可知，随着装药量的逐渐减少，炸药爆炸产生的损伤区域呈显著缩小的趋势。方案1中，在200 μs时爆炸形成圆柱形损伤区，此时损伤部位光滑平整；在500 μs时，模拟爆炸运行结束后孔底产生大面积破碎。方案2中，在200 μs时爆炸形成圆柱形光滑平整的受损区域；在500 μs时，岩石中部形成“喇叭状”的破坏损伤后未继续扩展，表明此时模拟爆炸的计算已经完成，底部水炮泥的存在缓解了应力波的冲击，对孔底损伤较小。方案3中，在200 μs时，爆炸形成了圆柱形损伤区，孔底无损伤；在500 μs时，2段装药柱完全起爆，上、下段形成“喇叭状”损伤，因底部水炮泥的存在缓解了应力波的冲击，孔底无损伤。方案4中，在200 μs时，爆炸形成了2段球型的破碎区域，损伤区光滑平整，无孔底损伤；在500 μs时，岩石破碎形成漏斗状破坏，损伤未继续扩展，表明此时模拟爆炸的计算已经完成，底部水炮泥的存在缓解了应力波的冲击，由于装药量较少，上、下2个药柱间未形成有效的爆破空腔。

为进一步说明4种装药结构的破碎范围，绘制了剖面损伤线，如图5所示。

图5 岩石损伤剖面线Fig.5 Rock damage profile lines

由图5可知，4种方案径向(x)最大破碎范围约为60 cm，轴向(y)最大破碎范围约为210 cm。

为了解4种装药结构起爆后对岩石内部损伤程度，提取各测点的损伤值并进行定量分析，如图6所示。由图6可知，RHT模型通过损伤值定义破碎范围，由测点Ⅰ，Ⅱ可知，在孔底水炮泥的作用下，岩石损伤值由全长装药的完全破碎(损伤值为1)变为局部损伤，减小了施工现场超挖的现象；测点Ⅲ，Ⅳ结合图5分析，在水炮泥的压缩下，分段装药也具有等长装药大致相同的轴向破碎距离，能够形成光滑的破碎范围，在一定程度上减少了炸药的单耗，节省了施工成本。

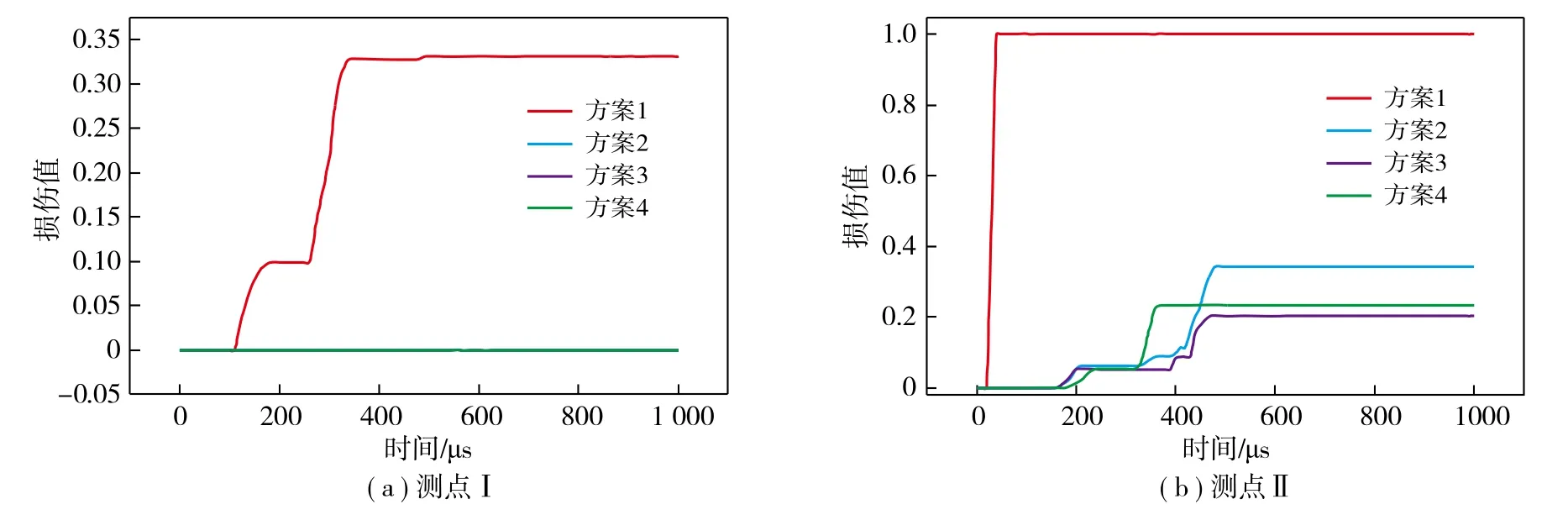
图6 各测点围岩损伤值曲线Fig.6 Curves of surrounding rock damage value of each measuring point

2.5 应力传播特性分析

为分析爆破过程中应力的变化趋势，提取各测点的有效应力并绘制成曲线，如图7所示。

图7 各测点有效应力时程曲线Fig.7 Effective stress time history curves of each measuring point

2.6 爆破后围岩振动特征分析

爆破振动作为爆破的危害之一[28]，必须在施工过程中引起足够的重视。为分析爆破后围岩振动特征，提取各测点的振速数据并绘制成曲线，如图8所示。由图8可知，在测点Ⅰ处，方案1，2，3的最大振速相近，约0.38 m/s；方案4的略小，约0.35 m/s。在测点Ⅱ处，方案1因无水炮泥封底而受到应力波的直接作用，速度瞬间增大至5.3 m/s左右；方案2，3，4因孔底受水炮泥黏滞性的影响，最大振速约0.35 m/s。对比测点Ⅰ和Ⅱ的数据可知，水的黏滞作用可以降低应力波对岩石的冲击作用。在测点Ⅲ处，方案3的最大振速约0.51 m/s；方案1，2的相近，约0.39 m/s；方案4的药量较少，起爆后测点受到的最大振速约0.28 m/s。在测点Ⅳ处，方案3的最大振速约0.7 m/s；方案2的约0.65 m/s；方案1，4的较小，其中方案1约0.41 m/s，方案4约0.32 m/s，这是由于方案1的装药结构中无水炮泥封堵孔底，应力波主要作用在孔底，径向测点受到的爆轰速度减小。对不同装药结构下炸药的有效破碎半径进行分析可知，方案1，2，3的破碎效果大致相同，径向破碎半径约为60 cm。因此，可根据数值模拟结果有针对性地对装药结构进行布置。

综上可知，方案1虽形成了光滑的圆柱形损伤区域，但同时导致孔底大面积破碎，且容易造成能量流失；方案2和方案3虽然装药量较少，但均产生了与方案1大致相同的损伤区域，能量得到了较为合理的利用；方案4由于装药量太少，并未形成有效的损伤区域。与方案1相比，方案2，3，4由于孔底水炮泥的存在，有效减弱了应力波对孔底的冲击，缩小了孔底的损伤范围，防止了施工现场超挖现象的发生。

3 底抽巷掘进面爆破数值模拟

3.1 模拟方案

为提高巷道掘进单次进尺深度，满足现场施工任务需要，对炮孔的装药结构和布置设计了2种模拟方案。方案1为井下生产实际布置，如图9(a)所示；方案2为根据单炮孔模拟结果对装药结构和炮孔布置进行优化后的改进方案，如图9(b)所示。

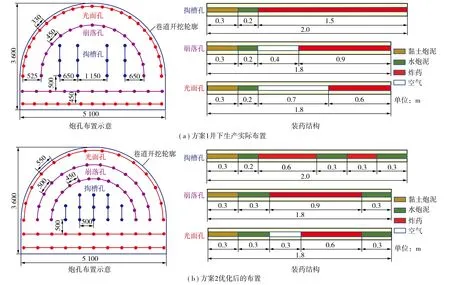
图9 2种方案的炮孔布置及装药结构Fig.9 Arrangement of blast holes and charging structures for two schemes

装药量统计见表4。

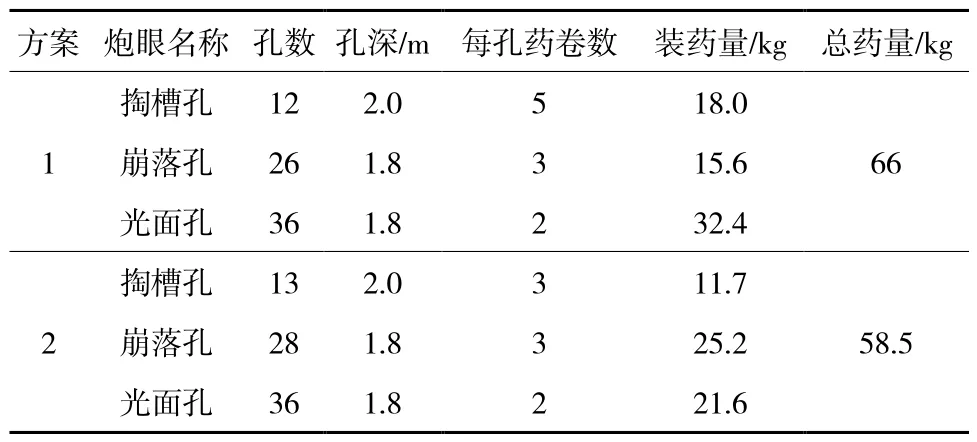
表4 装药量统计Table 4 Statistical table of drug dosage

3.2 模型构建

为更清晰地对比空气间隔装药与水间隔装药在巷道掘进中的优劣，建立全断面等比例模型模拟2种装药方案在掘进过程中的破岩情况，模型尺寸为10 m×10 m×3 m，如图10所示。

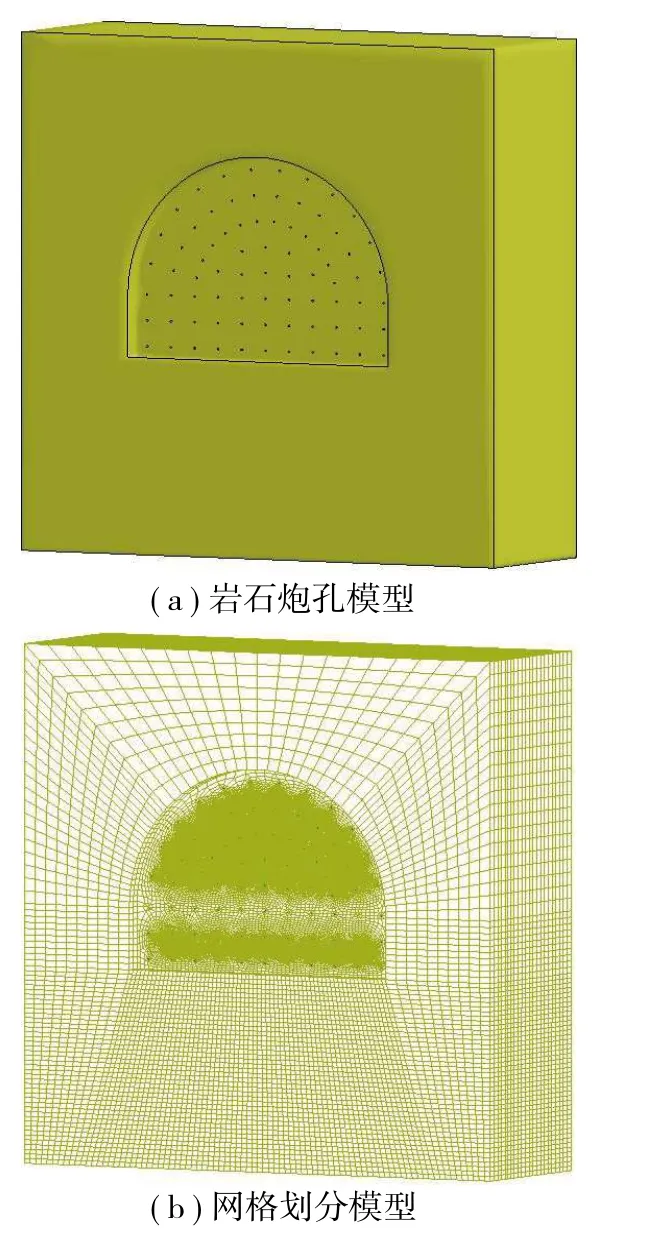
图10 巷道全断面爆破模型Fig.10 Full section blasting model of roadway

为避免因网格畸变严重而运算报错，炮孔采用映射网格划分，周围岩体采用扫掠划分。

由于爆炸分析过程较复杂，为了便于对结果进行分析，做如下基本假设：

3.1 气管导管固定的重要性 气管导管妥善固定对麻醉术中及术后的安全管理至关重要，稍有不慎，即可能造成严重的并发症。据报道，气管内插管的非计划拔管是常见的全身麻醉的主要并发症，甚至危及患者的生命安全［1-4］。气管导管妥善固定是手术顺利开展的先决条件，良好的导管固定方法是患者术中及术后安全管理的重要保障。

(1) 以网格变形来描述岩石破碎的过程，忽略实际施工过程中新自由面的产生对后续爆破的影响。

(2) 忽略岩石中节理裂隙对破岩的影响。

3.3 爆破效果分析

3.3.1 方案1 爆破效果分析

爆破模型方案1模拟采用集中装药结构，全部正向起爆。为了能直观观测到岩石内部爆破产生的破碎，沿模型轴向选取一系列截面，如图11所示，炮孔周围岩石的临界损伤程度用不同的颜色表示，损伤梯度从红色减小到绿色。由损伤剖面显示可知，损伤值由爆炸位置向外扩展时逐渐减小。

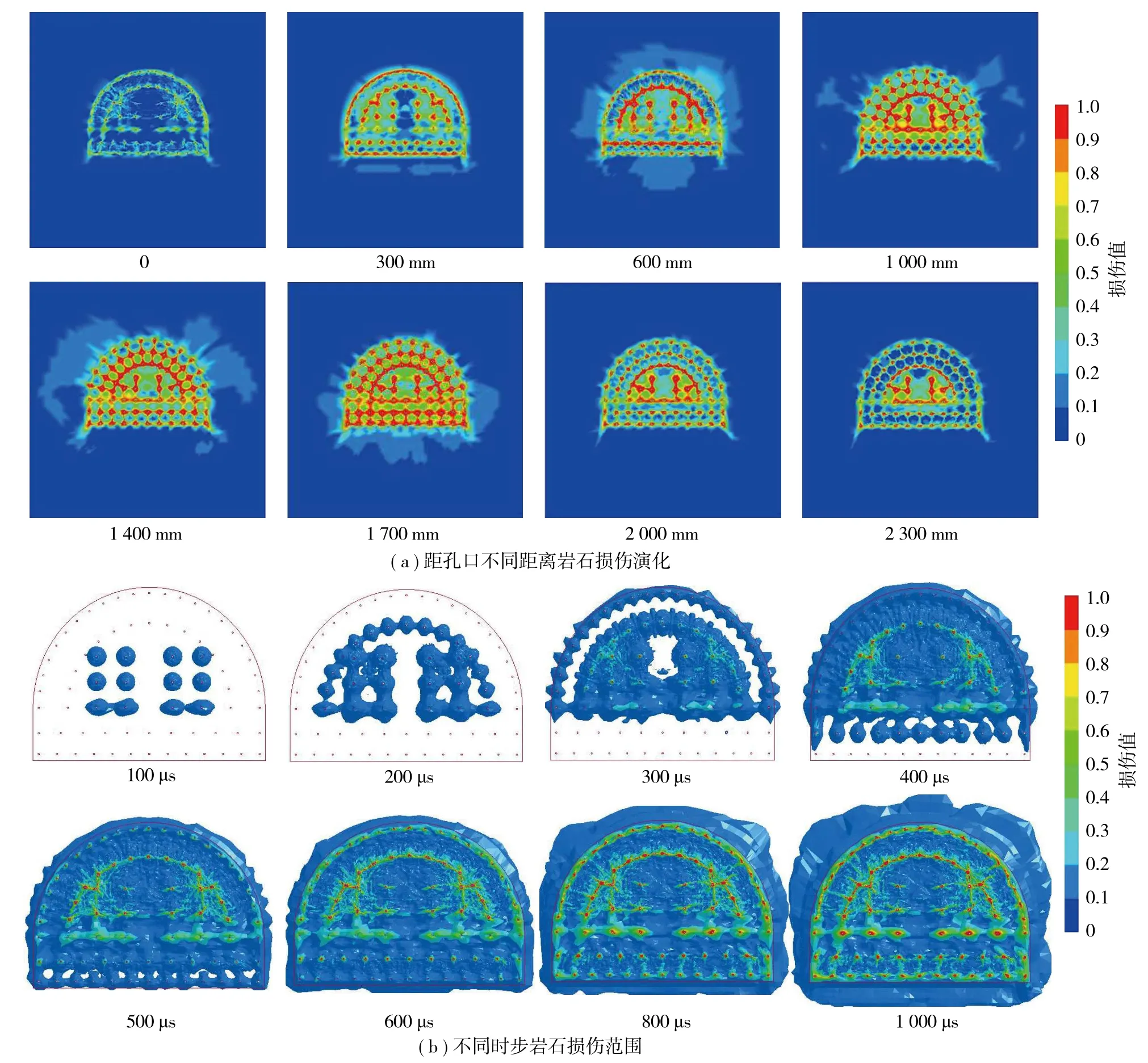
图11 方案1爆破损伤模拟结果Fig.11 Simulation results of blasting damage in scheme 1

由图11(a)可知，爆破结束后距孔口500 mm内，岩石破碎效果较差，虽然已炸出巷道轮廓，但是炮孔之间并未贯通，岩石并未被切分破碎，其依旧保持原有的完整性，且没有形成新的自由面，不能为上部岩石的抛掷提供空间；距孔口500～1 200 mm，因处于炸药的中心，爆破效果较好，形成了清晰的轮廓线，但炮孔之间并未被切分破碎，整体处于完整状态，并且掏槽孔间有未被扰动岩石，无法使用挖装机破碎清除；距孔口1 200～1 500 mm，已炸出巷道轮廓，炮孔之间并未贯通，但是对岩石的扰动较大，可以采用挖装机破碎清除；距孔口1 500～1 700 mm，岩石并未被切分破碎，其完整性高且未被扰动，无法实现破碎清除。由图11(b)可知，外侧光面孔在空气间隔下应力波在孔道内传递，在巷道外形成光滑的破碎区，对径向损伤较小，损伤半径约为5 cm。

3.3.2 方案2 爆破效果分析

爆破模型方案2模拟采用集中装药结构，全部正向起爆，爆破模拟结果如图12所示。

图12 方案2爆破损伤模拟结果Fig.12 Simulation results of blasting damage in scheme 2

由图12(a)可知，在炮孔口处的水炮泥和黏土炮泥共同作用下，应力波被压缩、减弱，虽然爆炸未完全破碎孔口，但岩石内已经产生损伤，可用挖装机掏碎清除，这既可以减少孔口岩石的抛掷，又能减少对附近机械的破坏，保护了施工人员的安全。距孔口300 mm处爆炸产生应力波相互叠加，对径向岩石进行破坏，使各炮孔之间相互贯通，岩石被切割成较小块体后形成环向的破碎区，并在动能作用下向自由面抛落；距孔口1 100 mm处属于炸药集中区，周围岩石破碎最为剧烈，炮孔之间完全贯通；距孔口1 100～1 800 mm处，周围岩石破碎后巷道轮廓清晰，炮孔之间的岩石均已完成切割；距孔口1 800～2 000 mm处，由于底部药量减少，岩石内部虽已被爆破，但其损伤度较低，挖装机无法实现破碎清除。

由图12(b)可知，爆破后岩体整体损伤区域光滑平整，对巷道扰动较小，爆破形成的轮廓轨迹满足现场的施工要求。

由上述2个方案的爆破模拟效果分析可知，采用优化后的方案，不仅总炸药用量减少，而且大幅提高了岩体的破碎范围和破碎程度，极大地破坏了岩体的完整性，使爆炸产生的裂纹在岩体内连接而切割了岩体，为后续爆破提供了新的自由面，并增加了巷道掘进的进尺深度，满足了岩巷掘进的要求。

4 工业性试验

试验地点为赵家寨矿14206工作面底抽巷，采用优化后的装药结构和炮孔布置方式。在实际施工中，由于岩体为非理想均质的弹性体，其含有原生裂隙和孔隙等，在爆破后水炮泥受高压冲击，水进入裂隙和孔隙中形成“水楔”，提高了岩石被爆后的破碎范围，优化后的巷道掘进进尺为1.8 m，炮孔利用率为90%。优化前后爆破效果对比如图13所示，采用优化装药结构和炮孔布置后，在水炮泥的黏滞作用下，爆破后的孔底光滑平整，无超欠挖发生。

图13 优化前后爆破效果对比Fig.13 Comparison of blasting effects before and after optimization

5 结 论

(1) 数值模拟了单孔爆破水间隔装药结构，合理的装药结构能产生与等长装药大致相同的损伤区域，且使能量得到较为合理的利用，减少炸药用量；孔底水炮泥有效减弱了应力波对孔底的冲击，缩小了孔底损伤范围，防止了施工现场超挖现象的发生。

(2) 由全断面分段装药爆破数值模拟结果可知，装药结构和炮孔布置优化改进方案相较于原方案，爆破后岩体整体损伤区域光滑平整，对巷道扰动较小，爆破形成的轮廓轨迹能够满足现场的施工要求，且减少了炸药损耗，节约了施工成本。

(3) 以赵家寨矿14206工作面底抽巷为试验地点，采用优化后的装药结构和炮孔布置方式。现场实测数据显示，优化后的炮孔利用率达到了90%，单次进尺可达1.8 m，且爆后掘进面平整光滑，无超欠挖现象发生。