地应力环境对深埋硐室岩爆特性影响的数值模拟研究

赵红亮，仇 岩，梁海安，杨泽平，张 娟

(东华理工大学 土木与建筑工程学院，江西 南昌 344000)

随着矿山建设、水利水电和油气开采等行业的蓬勃发展，我国地层的浅部资源正在日益枯竭，深部开采逐渐成为资源开发的常态。当岩体开挖深度超过700 m，工程开挖作业即进入深部地质环境，在深部地质环境下开挖的硐室被称为“深埋硐室”。与浅埋硐室相比，深埋硐室具有埋置深度大、原岩应力和地应力高等显著特征[1]。地应力赋存于岩体之中，是地下工程环境中最主要的指标之一，作为高地应力环境下特有的工程地质灾害现象，岩爆是硐室边缘部位应力集中超过了岩体的强度极限，从而导致岩体发生脆性破坏，并伴有围岩片帮剥落、弹射抛掷等动力失稳的现象[2]，在煤炭行业被称为冲击地压。轻微岩爆会使硐室围岩产生片帮现象，而强烈的岩爆往往会使岩石爆裂，崩出的破碎岩石会造成设备损坏、工期延误、人员伤亡等严重后果，岩爆问题已成为岩体地下工程和岩石力学领域的世界性难题。岩爆的产生与地应力聚集特性和地应力量级有着密切关系，一般来说，较高地应力区的岩体相较于较低地应力区的岩体，弹性模量更大，强度更高，储存的弹性变形能更多，更易产生岩爆。

王学滨[3]等利用FLAC模拟了不同围压条件下圆形巷道的岩爆过程，模拟结果表明，随着围压的增大，圆形巷道“V型”岩爆坑的破坏深度增加、圆形硐室附近剪切带花样的对称性变差，在高压状态下，剪切带花样与滑移线网有相似之处；肖繁[4]等基于最大主应力的岩爆判别准则，预测了巷道周边各部位的岩爆烈度等级，巷道不同部位的岩爆烈度等级由高到低依次为：底板两侧＞巷道两帮＞拱顶边缘；刘剑[5]等采用主成分分析法和改进贝叶斯(Bayes)判别法，选取岩石单轴抗压强度、脆性系数、岩石弹性能量等指标，建立了岩爆综合预测模型；陈卫忠[6]等按照地下工程开挖卸荷特点，开展了脆性花岗岩常规三轴、不同卸载速率条件下峰前、峰后三轴卸围压试验，探讨了岩爆岩石的变形破坏特征和岩爆形成力学机制；陈结[7]等对长期预测和短期预警方法及存在的问题、机器学习方法、冲击地压短期预警及长期预测的应用，以及传统的经验驱动和机理驱动与机器学习的数据驱动在冲击地压预测预警方面的联系与差异做了总结；罗天敏[8]等对国家能源集团新疆能源有限责任公司下属矿井冲击地压监测预警现状进行了分析，提出了多参量集成监测预警平台本地化建设方案；杨凡杰[9]等为了对岩爆进行更准确的预测，结合试验和理论分析认为，岩爆机制的研究在本质上应是对岩体中裂纹动态扩展问题的研究，进而提出一个新的岩爆能量判别指标——单位时间相对能量释放率指标；张修峰[10]等通过冲击地压多参量联合监测预警方法研究、监测监控平台系统开发和现场实践，探索了新形势下冲击地压监控预警新模式，实现了矿井与防冲研究中心、井上与井下、静态数据与动态数据、预警结果与现场处置措施等智能联动及自动上报；吕鹏飞[11]等提出一种基于粒子群算法(PSO)优化最小二乘支持向量机(LSSVM)预测方法，即冲击地压分级预测的PSO-LSSVM方法，该方法综合考虑煤矿开采深度、地质构造、煤的坚固性系数、最大主应力、煤层倾角变化、煤厚变化、顶板岩层厚度、开采工艺、顶板和底板岩石强度共10项指标因素，构建冲击地压预测指标体系；陈卫忠[12]等开展脆性花岗岩常规三轴、不同控制方式、不同卸载速率条件下，峰前、峰后卸围压试验，从能量的原理探讨岩石破坏过程能量积聚-释放的全过程，研究岩石的变形破坏特征、能量集聚-耗散-释放特征和基于能量原理的岩爆判据；姚精明[13]等采用物理实验和多重分形理论相结合的方法，研究了煤样变形破坏过程中多重分形谱宽度与其冲击倾向、释放能量的内在关系；吕森鹏[14]对实际工程中岩爆的发生机理、预测预报模型开展试验与理论研究、对岩爆防治对策进行实际探讨，从而提出了可靠的预测方法和防治对策；陈玉涛[15]提出一种邻近地质构造的不规则孤岛工作面冲击危险性评价方法；夏永学[16]等针对综合指数法和多因素耦合法在进行冲击危险性评价时存在临界突变和权重量化困难等问题，通过因素分类、指数叠加和归一化处理，建立了改进的综合指数方法；宫凤强[17]等基于现有的岩爆分级判据分析高地应力环境下围岩的破坏现象，提出了高地应力“强度&应力”耦合判据及其定量分级标准，结果表明，基于岩石强度和地应力两种要素提出的“强度&应力”耦合判据能够在众多工程实例检验结果中证实该判据的合理性；荣海[18]等对坚硬岩层结构特征、结构形成条件、结构失稳尺度、结构失稳释放能量等进行了分析，并分别给出了相应的计算公式，确定坚硬岩层失稳对冲击地压的控制作用。

综上所述，现有的研究大都从影响岩爆产生的单一因素作为出发点，引入岩爆判别指标，判断地应力对岩爆特征的影响，但是影响岩爆产生的因素具有多样性，仅凭单一的岩爆判别指标研究地应力对岩爆特征的影响过于片面，因此笔者在前人研究的基础上，利用硬岩在某个特定围压状态下的试验数据，拟合出了硬岩的极限储能值经验公式，从导致岩爆发生的能量角度和应力角度出发，引入了弹性变形能和岩石应力强度比作为岩爆发生的判别指标，通过FLAC3D数值模拟技术输出岩爆判别指标云图和监测曲线，结合相关岩爆倾向判据分析地应力环境对岩爆烈度等级和破坏区域的影响。

1 岩爆的评价指标和判据

1.1 弹性变形能指标

基于弹性变形能理论，岩体产生破坏主要是能量驱动的结果。当岩体可释放的弹性变形能Ue达到岩体破坏所需的极限储能U0时，也即Ue=U0时，岩体内部弹性变形能完全释放，岩体产生静态破坏，此时不会发生岩爆灾害；当Ue=U0时，岩体发生动态破坏，诱发岩爆的产生。

弹性变形能作为表征岩爆现象发生的物理量，能够结合相关岩爆判别准则来对岩爆发生的烈度等级进行分析。

岩体发生岩爆破坏的条件为

针对岩石的极限储能值U0，笔者结合文献[6，12，14]中有关花岗岩在加、卸载速率为0.1 MPa/s，不同控制方式下的极限储能结果(表1)，拟合得到了其在特定围压状态下的极限储能经验公式，拟合曲线如图1所示。

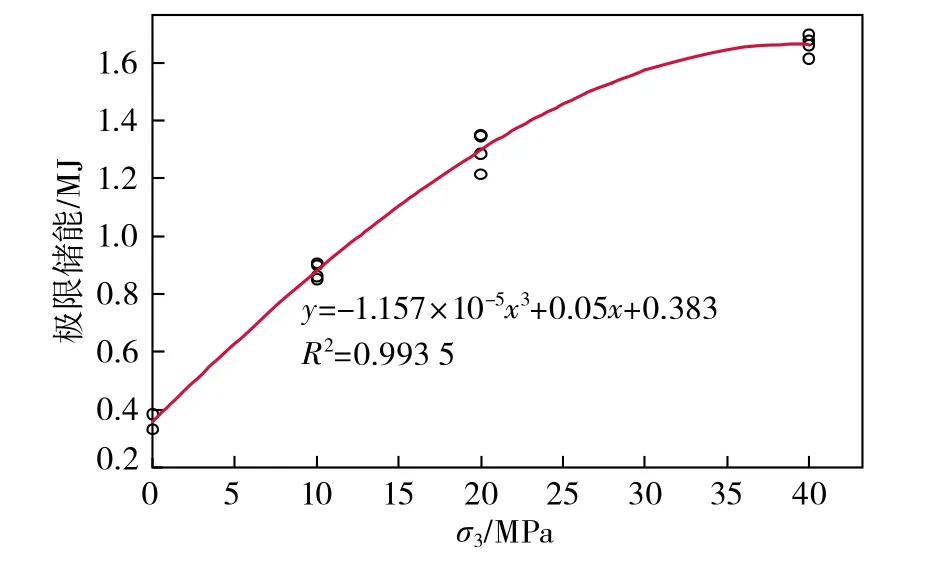
图1 岩石极限储能与围压拟合曲线Fig.1 Fitting curve of rock limit energy storage and confining pressure

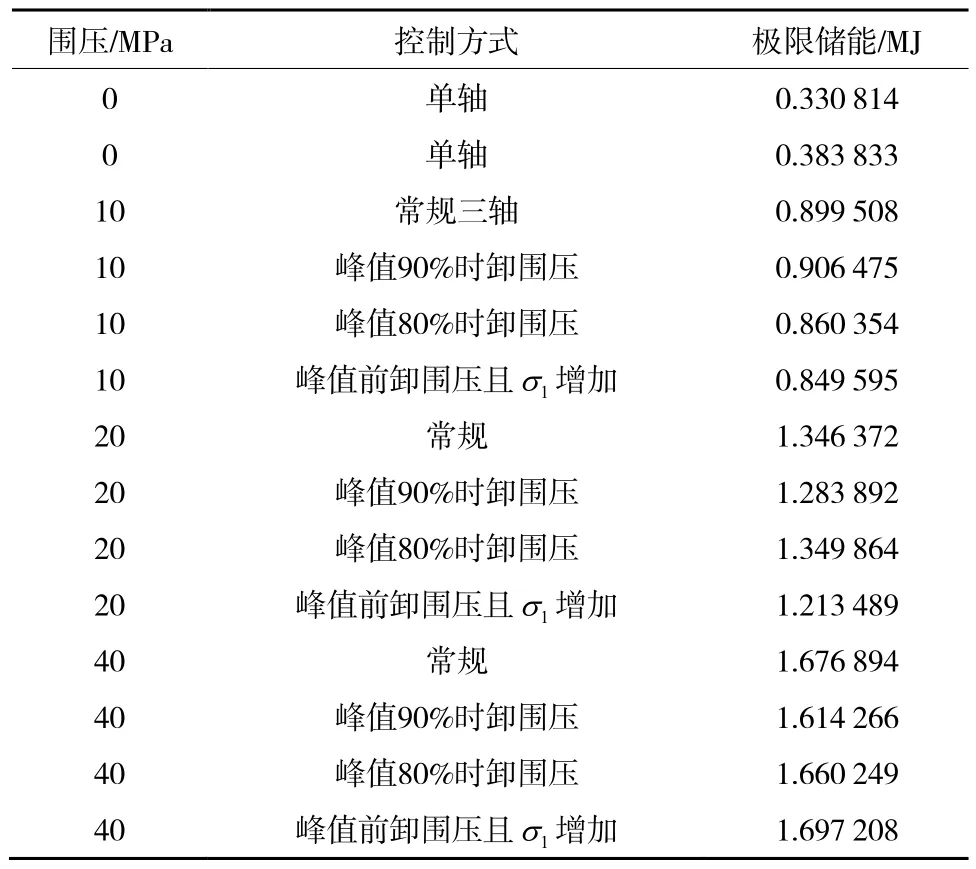
表1 花岗岩在不同控制方式下的极限储能Table 1 Limit energy storage of granite under different control methods

极限储能经验公式为

弹性变形能物理表达式为

式中，σ1,σ2,σ3为单元体的3个主应力；μ为泊松比；E为弹性模量。

1.2 能量判别准则

陈卫忠[12]等定义岩爆能量指数为岩体单元的真实能量U与岩石极限储能U0的比值，具体判据为

1.3 岩石应力强度比指标

HOEK[20]根据南非矿井的巷道破坏情况，利用岩石单轴抗压强度和硐壁切向应力建立了表征岩爆与硐室围岩应力关系的岩石应力强度比指标，即

式中，σθ为硐壁切向应力；σc为岩石单轴抗压强度。

E.Hoek判别准则为

2 数值模拟结果分析

2.1 数值模型及岩石力学参数

硐室的长度远大于其截面尺寸时，可视为平面应变问题，在FLAC3D程序中建立准三维数值计算模型，如图2所示。

图2 硐室三维数值计算模型Fig.2 Three-dimensional numerical model of chambers

模拟工况为：开挖隧硐埋深为1 500 m，模型尺寸为50 m×50 m，中央位置处为直径10 m的圆形待开挖隧硐，左右两侧边界施加水平方向位移约束，前后边界施加水平方向位移约束，底部边界施加垂直和水平方向位移约束，上部边界施加上覆岩体自重应力。先对模型施加初始地应力场，当计算达到应力平衡状态后，再开挖圆形硐室。假设岩体为均质各向同性，并采用FLAC3D内置的Morh-Coulomb本构模型。数值计算采用的花岗岩物理力学参数为：弹性模量E为50 GPa，泊松比为0.2，容重为26.9 kN/m3，黏聚力c为2.6，内摩擦角为43°。

2.2 不同地应力环境下主应力差分布特征

岩爆是高应力集中的结果，因此应着重关注硐室周围的应力集中区域。岩爆产生的破坏类型多为压剪破坏，导致岩体破坏的剪切应力可由主应力差间接表示。由于FLAC3D数值分析软件无法直接输出模型的主应力差，笔者基于主应力差理论，利用FISH语言进行软件的二次开发，从而实现主应力差云图的输出。

图3为不同侧向压力系数时的圆形硐室主应力差云图。考虑到实际工程当中面临的地应力环境不同，笔者通过侧向压力系数λ为0.50，0.75，1.50，2.00时的模拟结果，分析地应力最大主应力方向对硐室岩爆产生的影响。

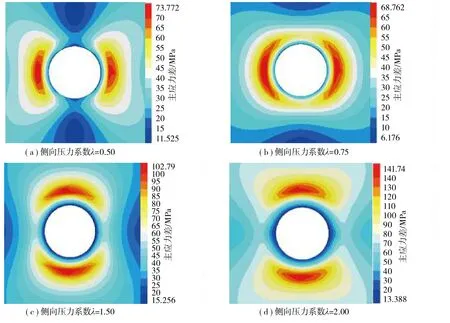
图3 圆形硐室主应力差分布云图Fig.3 Cloud map of main stress difference distribution in circular chambers

由图3可知，受开挖扰动的影响，围岩应力在一定范围内重新分布，越靠近圆形硐室周边区域，围岩主应力差的分布不均匀性越显著，随着开挖远离圆形硐室边缘，主应力差分布不均匀程度明显降低。

当地应力场中的水平应力小于竖向应力(λ＜1.0)时，硐室两侧的应力集中情况较为显著，主应力差最大值位于硐室两侧，对应硐室两侧的剪应力集中程度较为明显。应力集中区距离硐室边缘约1.2 m，最大主应力差为68.762～73.772 MPa，该状态下可能发生岩爆灾害的区域主要为硐室两侧。

当地应力场中的水平应力大于竖向应力(λ＞1.0)时，硐室顶部和底部的应力由应力释放状态转变为应力集中状态，对应硐室顶部和底部区域的剪应力集中程度较为显著，应力集中区距离硐室边缘约3.1 m，最大主应力差为102.79～141.74 MPa，该状态下可能发生岩爆的区域主要为硐室的顶部和底部位置。

2.3 不同地应力环境对硐室岩爆的发生及烈度等级的影响

2.3.1 弹性变形能变化特征及分析

基于弹性变形能理论得到岩体单元弹性变形能量公式(3)，利用FLAC3D内嵌FISH语言编写计算函数，输出圆形硐室弹性变形能云图，通过岩体开挖后硐室周围能量的变化，分析侧向压力系数对岩爆的影响。

图4为不同侧向压力系数下，圆形硐室的弹性变形能分布云图，当λ＜1.00时，弹性变形能积聚区位于硐室两侧，弹性变形能的释放区域位于硐室的顶部和底部；当λ=0.50 时，弹性变形能最大值为1.939 5 MJ；当λ=0.75 时，弹 性 变形 能最 大 值为1.838 4 MJ。当λ＞1.00时，弹性变形能的积聚区域由硐室的两侧转变为硐室的顶部和底部；当λ=1.5时，弹性变形能最大值为4.766 9 MJ；当λ=2.00时，弹性变形能最大值为5.326 MJ。

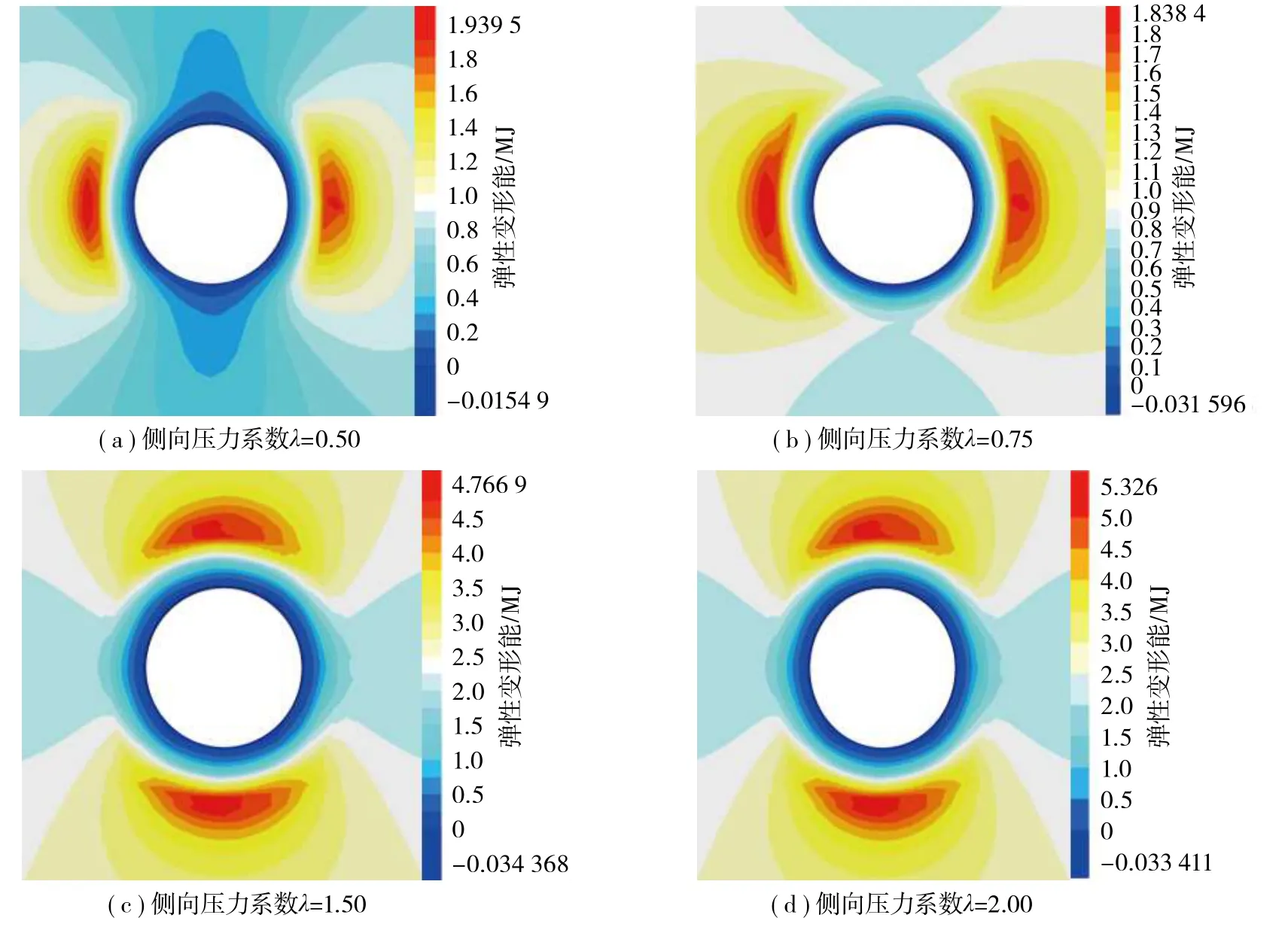
图4 圆形硐室弹性变形能分布云图Fig.4 Cloud map of elastic deformation energy distribution in circular chambers

由弹性变形能分布特征可知，地应力环境的变化会影响硐室周边弹性变形能积聚区的分布及数值的变化，相应地发生岩爆破坏的部位和烈度等级也会发生变化。当λ＜1.00时，弹性变形能的积聚区域位于硐室两侧，对应硐室两侧发生岩爆的可能性较硐室其他部位大；当λ＞1.00时，弹性变形能积聚区域由硐室两侧位置转移至硐室的顶部和底部，对应硐室顶部和底部两处位置发生岩爆的可能较硐室其他部位大。

为了进一步探究侧向压力系数λ对硐室岩爆特征的影响，在圆形硐室周围布置监测点，监测岩体开挖后弹性变形能的变化，得到硐室周围弹性变形能变化曲线，结合岩爆能量判据对圆形硐室岩爆发生的破坏区域和烈度等级进行分析。由于模拟岩体为均质各向同性，开挖圆形硐室上下左右均对称，因此在圆形硐室顶部、腰部分别布置一排5个监测点，如图5所示。

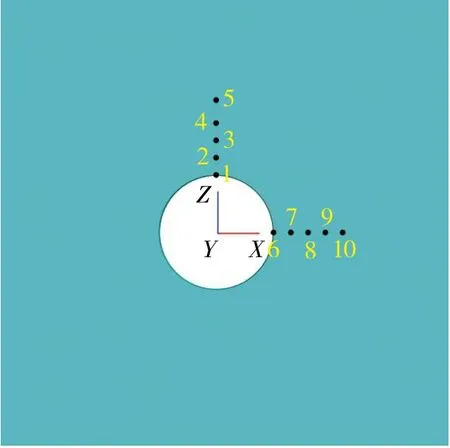
图5 圆形硐室监测点布置示意Fig.5 Layout diagram of monitoring points in circular chamber s

由图6(a)和图4(a)可知，当λ=0.50时，硐室顶部和底部的能量整体处于弹性变形能释放状态，岩体内部不存在弹性变形能积聚区，且各监测点的能量均未超过岩石的储能极限值，因此硐室顶部和底部不会发生岩爆灾害。

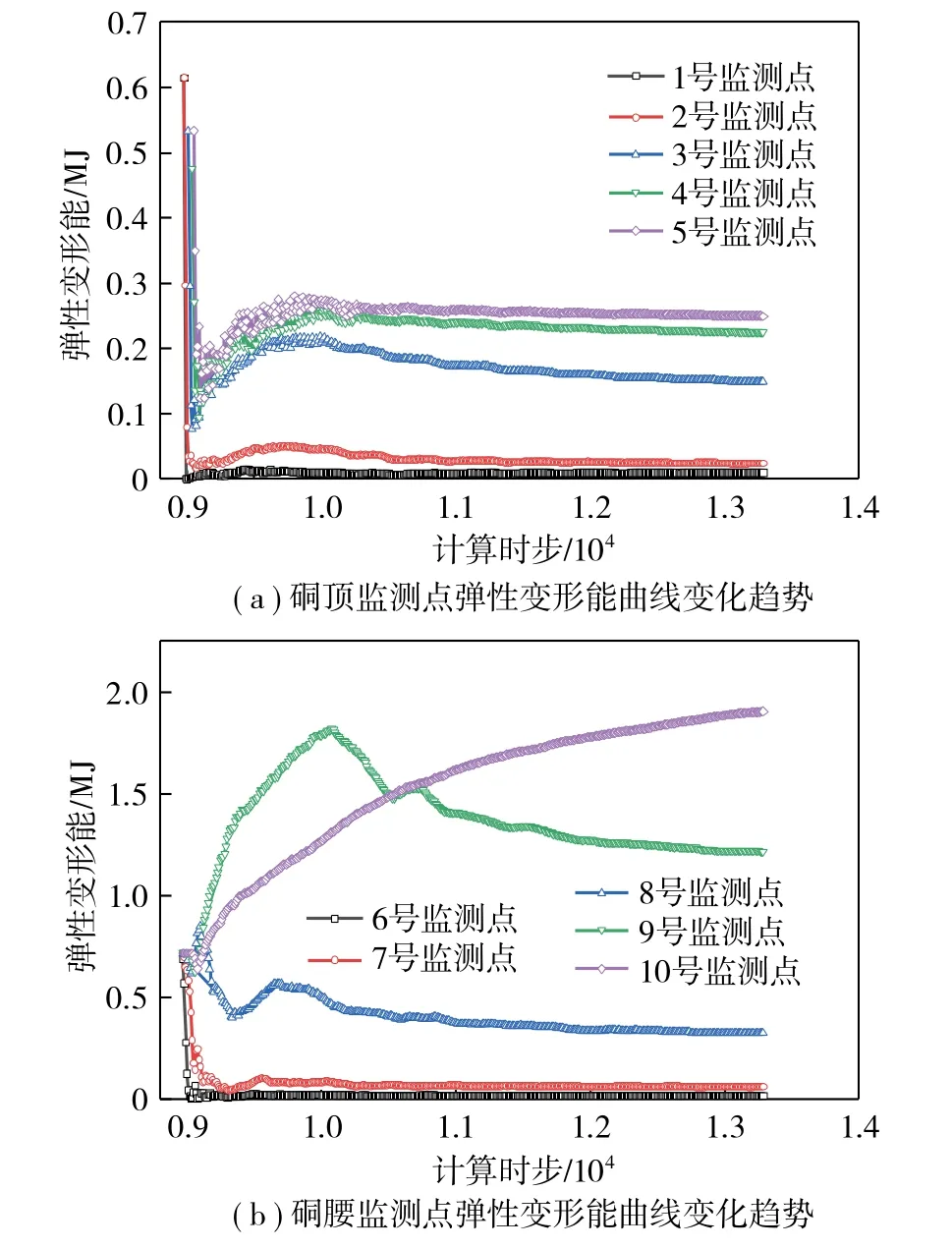
图6 λ=0.50 时硐室周围监测点弹性变形能变化曲线Fig.6 Variation trend of the elastic deformation energy curves of the monitoring point around the chambers when λ=0.50

由图6(b)可知，6号监测点岩体单元的能量U6=0.68 MJ，岩体单元能量超过岩石的极限储能值U06=0.42 MJ，岩爆能量指数U6/U06=1.6，因此硐室腰部6号监测点岩体单元存在岩爆风险；7号监测点岩体单元的能量U7=0.72 MJ，岩体单元能量超过岩石的极限储能值U07=0.50 MJ，岩爆能量指数U7/U07=1.4，因此硐室腰部7号监测点岩体单元存在岩爆风险；8号监测点岩体单元的能量U8=0.63 MJ，岩体单元能量超过岩石的极限储能值U08=0.62 MJ，岩爆能量指数U8/U08=1.0，因此硐室腰部8号监测点岩体单元存在岩爆风险。结合岩爆能量判据可知，硐室两侧表现为IV级强烈岩爆倾向。应力的调整使得能量积聚区向岩体内深部转移，由岩体内部9号和10号监测点弹性变形能增量的变化，结合图4(a)可知，圆形硐室腰部两侧的弹性变形能积聚区距离 硐室边缘约3.8 m，影响范围约2.5 m。

图7为λ=0.75时硐室周围监测点的弹性变形能变化曲线。

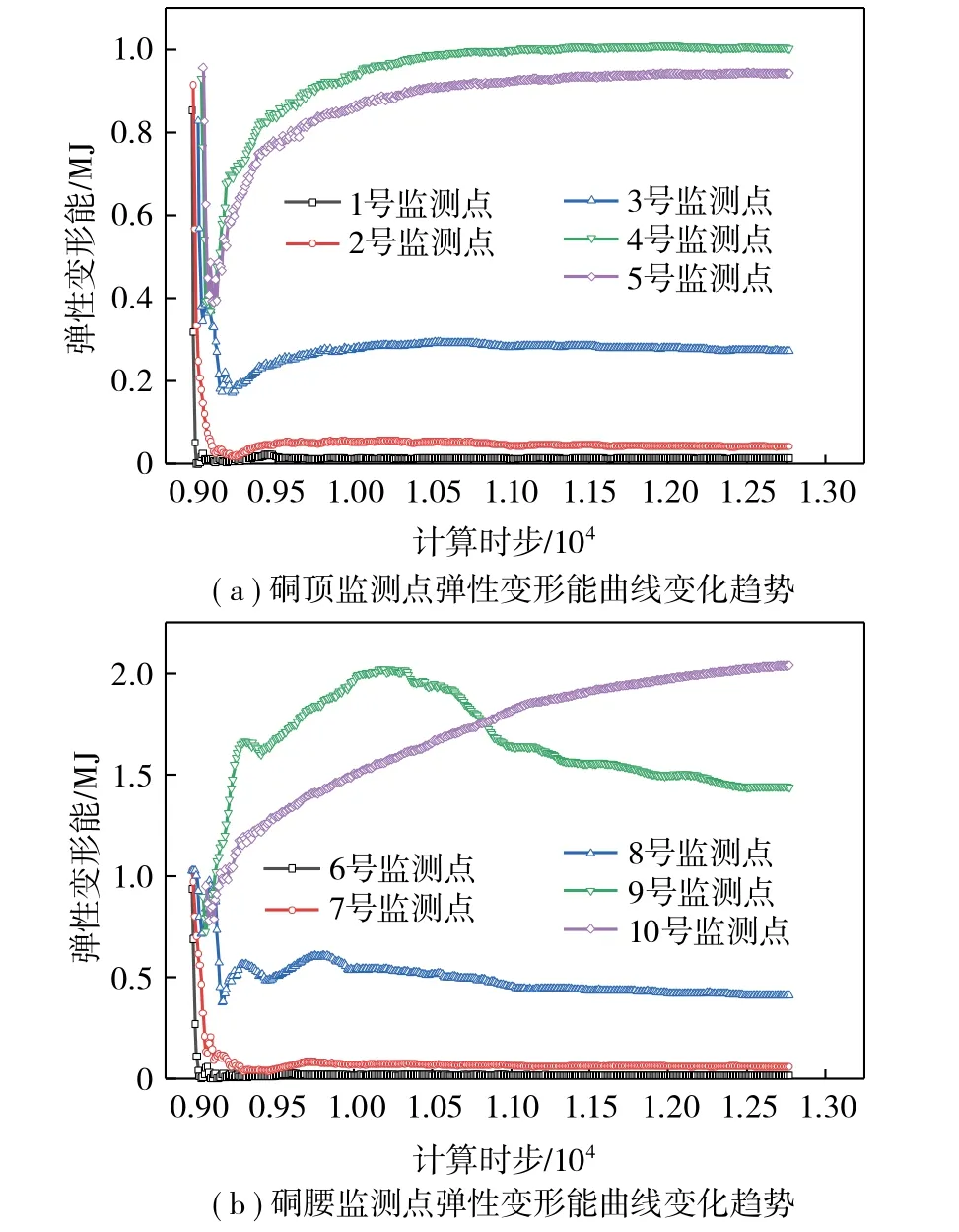
图7 λ=0.75 时硐室周围监测点的弹性变形能变化曲线Fig.7 Variation trend of the elastic deformation energy curves of the monitoring point around the chambers when λ=0.75

由图7(a)和图4(b)可知，当λ=0.75时，圆形硐室顶部和底部的能量整体处于弹性变形能释放状态，岩体内部不存在弹性变形能量积聚区，且各监测点的能量均不超过岩石的储能极限值，因此硐室顶部和底部不会发生岩爆灾害。

由图7(b)可知，6号监测点岩体单元的能量U6=0.94 MJ，岩体单元能量超过岩石的极限储能值U06=0.90 MJ，岩爆能量指数U6/U06=1.0，因此硐室腰部6号监测点岩体单元存在岩爆风险；7号监测点岩体单元的能量U7=1.03 MJ，岩体单元能量超过岩石的极限储能值U07=0.95 MJ，岩爆能量指数U7/U07=1.1，因此硐室腰部7号监测点岩体单元存在岩爆风险；8号监测点岩体单元的能量U8=1.03 MJ，岩体单元能量超过岩石的极限储能值U08=0.98 MJ，岩爆能量指数U8/U08=1.1，因此硐室腰部8号监测点岩体单元存在岩爆风险。结合岩爆能量判据可知，硐室两侧表现为IV级强烈岩爆倾向。应力的调整使得能量积聚区向岩体内部转移，由岩体内部9号和10号监测点弹性变形能增量的变化，结合图4(b)可知，圆形硐室腰部两侧的弹性变形能量积聚区域距离硐室边缘约3.4 m，影响范围约2.0 m。

图8为λ=1.50时硐室监测点的弹性变形能曲线。

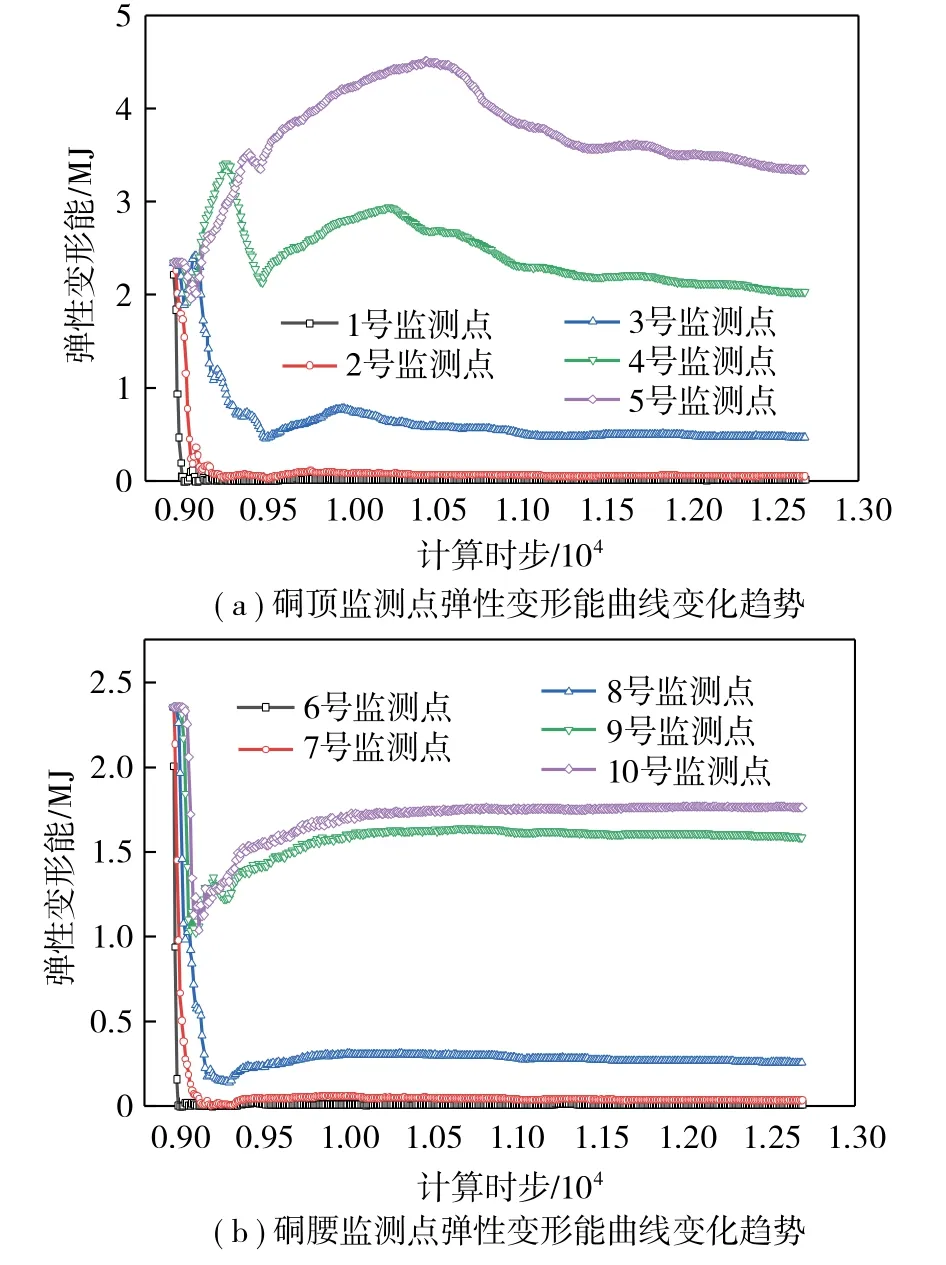
图8 λ=1.50 时硐室周围监测点弹性变形能变化曲线Fig.8 Variation trend of the elastic deformation energy curves of the monitoring point around the chambers when λ=1.50

由图8(b)和图4(c)可知，当λ=1.50时，圆形硐室腰部两侧的能量整体处于弹性变形能释放状态，岩体内部不存在弹性变形能量积聚区，因此腰部两侧不会发生岩爆灾害。

由图8(a)可知，1号监测点岩体单元的能量U1=2.20 MJ，岩体单元能量超过岩石的极限储能值U01=1.24 MJ，岩爆能量指数U1/U01=1.8，因此硐室顶部1号监测点岩体单元存在岩爆风险；2号监测点岩体单元的能量U2=2.35 MJ，岩体单元能量超过岩石的极限储能值U02=1.35 MJ，岩爆能量指数U2/U02=1.7，因此硐室顶部2号监测点岩体单元存在岩爆风险；3号监测点岩体单元的能量U3=2.40 MJ，岩体单元能量超过岩石的极限储能值U03=1.40 MJ，岩爆能量指数U3/U03=1.7，因此硐室顶部3号监测点岩体单元存在岩爆风险；结合岩爆能量判据可知，硐室顶部和底部表现为IV级强烈岩爆倾向。应力的调整使得能量积聚区向岩体内部转移，由岩体内部4号和5号监测点弹性变形能增量的变化，结合图4(c)可知，圆形硐室顶部和底部的弹性变形能量积聚区域距离硐室边缘约4.1 m，影响范围约4.6 m。

图9为λ=2.00时硐室监测点的弹性变形能曲线。

图9 λ=2.00 时硐室周围监测点弹性变形能变化曲线Fig.9 Variation trend of the elastic deformation energy curves of the monitoring point around the chambers when λ=2.00

由图9(b)和图4(d)可知，当λ=2.00时，圆形硐室腰部两侧的能量整体处于弹性变形能释放状态，岩体内部不存在弹性变形能量积聚区，因此腰部两侧不会发生岩爆灾害。

由图9(a)可知，1号监测点岩体单元的能量U1=2.50 MJ，岩体单元能量超过岩石的极限储能值U01=0.98 MJ，岩爆能量指数U1/U01=2.6，因此硐室顶部1号监测点岩体单元存在岩爆风险；2号监测点岩体单元的能量U2=2.60 MJ，岩体单元能量超过岩石的极限储能值U02=1.10 MJ，岩爆能量指数U2/U02=2.4，因此硐室顶部2号监测点岩体单元存在岩爆风险；3号监测点岩体单元的能量U3=2.70 MJ，岩体单元能量超过岩石的极限储能值U03=1.30 MJ，岩爆能量指数U3/U03=2.1，因此硐室顶部3号监测点岩体单元存在岩爆风险；结合岩爆能量判据可知，硐室顶部和底部表现为IV级强烈岩爆倾向。应力的调整使得能量积聚区向岩体内部转移，由岩体内部4号和5号监测点弹性变形能增量的变化，结合图4(d)可知，圆形硐室顶部和底部的弹性变形能量积聚区域距离硐室边大约4.5 m，影响范围约5.8 m。

2.3.2 岩石应力强度比变化特征及分析

利用岩石应力强度比来表征岩爆与硐室围岩应力的关系，基于FISH语言编写岩石应力强度比公式(4)的计算函数，通过提取应力集中区监测点的最大切向应力，替代弹性分析中硐壁最大切向应力的解析解，输出圆形硐室岩石应力强度比云图，从力学角度研究不同侧向压力系数λ对硐室岩爆特征的影响。

图10为不同侧向压力系数λ下圆形硐室岩石应力强度比云图。

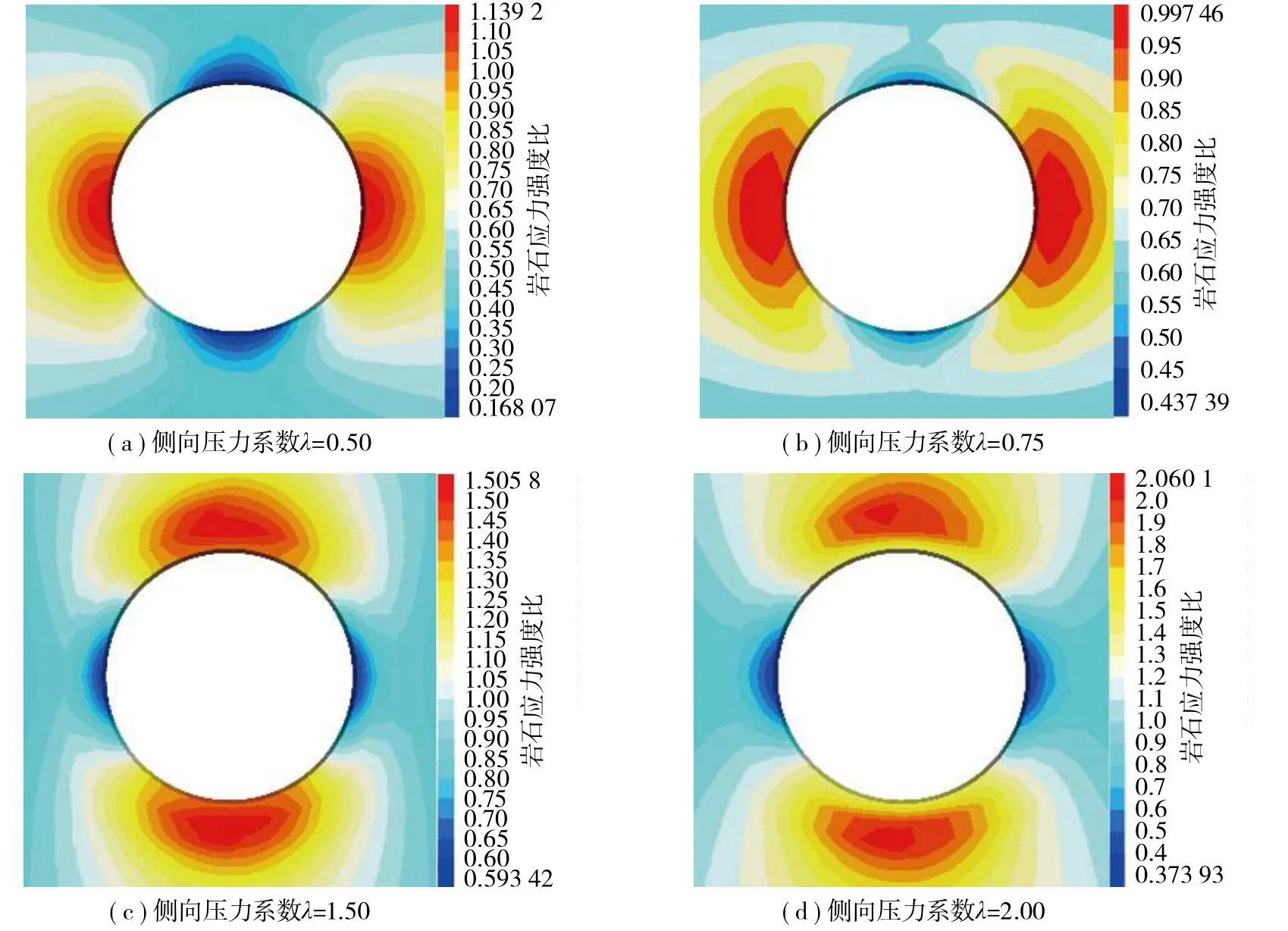
图10 不同侧向压力系数λ 下圆形硐室岩石应力强度比云图Fig.10 Rock strength stress ratio nephogram of circular chambers under different lateral pressure coefficients

由图10可知，当λ＜1.00时，岩石应力强度比的最大值位于硐室两侧；当λ=0.50时，岩石应力强度比最大值为1.139 2；当λ=0.75时，岩石应力强度比最大值为0.997 46，结合E.HOEK岩爆判据可知硐室两侧部位表现为IV级强烈岩爆倾向。当λ＞1.00时，岩石应力强度比的最大值位于硐室顶部和底部；当λ=1.50时，岩石应力强度比最大值为1.505 8；当λ=2.00时，岩石应力强度比最大值为2.060 1，结合E.HOEK岩爆判据可知硐室顶部、底部表现为IV级强烈岩爆倾向。

3 结 论

(1) 当λ＜1.00时，应力集中区域和弹性变形能聚集区位于硐室两侧，随着侧向压力系数λ的增加，应力集中区的主应力差最大值降低，能量聚集区的弹性变形能数值逐渐下降。应力重新分布后，围岩内部弹性变形能聚集区向岩体内部转移的距离由3.8 m缩小至3.4 m，对应岩爆产生的风险变小，破坏深度减小。

(2) 当λ＞1.00时，应力集中区域和弹性变形能聚集区域位于硐室顶部和底部，随着侧向压力系数λ的增加，应力集中区的主应力差最大值增大，能量聚集区的弹性变形能数值逐渐增加。应力重新分布后，围岩内部弹性变形能聚集区向岩体内部转移的距离由4.1 m增加至4.5 m，对应岩爆产生的风险变大，破坏深度增大。

(3) 不侧向压力系数λ下，硐室存在岩爆灾害的风险等级均表现为IV级强烈岩爆。当λ＜1.00时，产生岩爆的部位在硐室两侧，随着侧向压力系数λ的增大，该部位的岩石应力强度比逐渐减小，对应岩爆发生的风险减小，破坏范围缩小；当λ＞1.00时，产生岩爆的部位在硐室顶部和底部，随着侧向压力系数λ的增大，岩石应力强度比值由1.5增大至2.1，对应岩爆产生的风险变大，破坏范围增大。

笔者借鉴国内相关学者对岩石储能机制的相关试验研究，重新拟合了不同围压下花岗岩的极限储能经验公式，引用相应的岩爆指数能量判别准则用于表征岩石受载过程中的储能特征和能量转化，可以较好地从能量角度解释岩石工程失稳破坏机制，但限于岩石力学试验的复杂性，对加卸载速率的影响考虑还不够充分，尚有不足之处。