基于AO优化VMD-小波包的岩石破裂声发射信号去噪算法

王婷婷，李 方，霍雨佳，王振豪，赵万春

(1.东北石油大学 电气信息工程学院，黑龙江 大庆 163318；2.东北石油大学 黑龙江省网络化与智能控制重点实验室，黑龙江 大庆 163318；3.东北石油大学 非常规油气研究院，黑龙江 大庆 163318；4.东北石油大学 陆相页岩油气成藏及高效开发教育部重点实验室，黑龙江 大庆 163318)

岩体受应力或载荷作用时，内部会发生微小的变形进而产生微裂纹。在此过程中，储存的能量会释放出来，并以弹性波的形式在介质中传播，这种现象称之为声发射(Acoustic Emission，AE)现象[1]。岩石破裂过程中的声发射信号可以反映岩体破裂的过程，对其进行处理和分析可较为准确地揭示岩体破裂的位置、裂缝形成的类型及岩体损伤的程度等，有利于预防由于岩石失稳破坏过程所导致的工程事故与灾害[2]。

在实际工程或岩石力学试验中，外界嘈杂的环境及设备间的摩擦等背景噪声也被传感器接收，因此设备收集到的声发射信号会包含部分无效噪声，影响后续的处理分析进而丧失预测的准确性。因此，对实测声发射信号进行降噪预处理十分必要[3]。

声发射信号是一种非线性、非平稳的信号，目前，常见的去噪方法有：傅里叶变换(FT)、小波变换(WT)、经验模态分解(EMD)、完全自适应噪声集合经验模态分解(CEEMDAN)、小波包分解、变分模态分解(VMD)等[4-5]。其中，单纯采用傅里叶变换进行去噪，效果并不理想[6]；小波变换适合分析随机非平稳信号，对于降噪处理受限于小波基函数的选择等[7]；经验模态分解在信号降噪处理过程中会伴随模态混叠现象，去噪的同时会消除部分有效信号，易造成失真[8]；小波包分解也称为小波包，是改进的小波变换，它对信号的高、低频分量均进行分解，比小波变换更全面、细致，但单纯使用小波包算法进行信号去噪同样会受限于小波基函数、阈值类型等的选取，使得信号降噪过程变得困难[9]。针对上述问题，2014年，UCLA的DRAGOMIRETSKIY[10]等提出了变分模态分解(Variational Mode Decomposition，VMD)算法，这是一种信号分解估计方法，相较于传统分解算法其对于干扰量具有更强的鲁棒性，分解速度更快，因此很快被信号处理领域广泛应用。苏梦哲[11]等就使用VMD对含有干扰分量的微震信号进行了降噪处理，结果表明VMD很好地去除了信号中的噪声，获得的信号更接近原始信号；戚庭野[12]等提出一种基于鲸鱼算法优化变分模态分解(WOAVMD)参数的方法并对瞬变电磁信号进行降噪处理，获得的信号信噪比和均方误差均较好。虽然VMD在信号降噪方面表现优异，但随着研究的深入该算法的一些不足也暴露出来，如处理信号前需人为设定固定的分解模态个数K和二次惩罚因子α，在此过程中取值过大或过小都会对分解精度造成影响[13]。

为充分发挥VMD和小波包的优点并合理规避两种算法的不足，笔者提出了一种优化改进的VMD和小波包联合的去噪方法。在此方法中，首先引入天鹰优化(Aquila Optimizer，AO)算法对VMD进行改进，由改进的天鹰优化(Improved Aquila Optimizer，IAO)算法寻优得到VMD分解所需的最优参数，取代人为设定参数，最大限度地保证了分解精度；然后，计算每个分量与原始AE信号的相关系数，通过相关系数来区分出含噪和未含噪分量，并采用小波包去噪方法对含噪分量进行去噪，将去噪后的分量与未含噪分量合并重构，输出去噪后的信号；最后，通过仿真及实测信号验证，结果表明与小波包、CEEMDAN-小波包、WOA-VMD去噪算法相比，此算法能够更精准地抑制噪声，性能更优。

1 降噪算法基本原理

1.1 VMD算法原理阐述

变分模态分解(VMD)算法是将一组信号非递归分解成K个具有准正交性及特定稀疏性本征模态函数(IMF)，实现信号的有效分离。VMD算法是基于Wiener滤波、Hilbert变换以及频率混合等概念得来的[14]，其整体思路是构造变分问题。变分约束需要满足所有分量之和与原本信号一致，约束变分模型为

式中，{uk}为VMD分解后得到的K个本征模态分量，{u1,u2,… ,uk}；{wk}为K个本征模态分量各自的中心频率，{w1,w2,… ,wk}；f(t) 为原始信号；∂t为梯度计算符号；δ(t)为狄拉克雷函数；*为卷积运算符号；s.t.为约束项。

为解决变分约束问题，完成由约束性问题到非约束性问题的转化，引入拉格朗日算子λ以及二次惩罚因子α，变换后得到增广Lagrange计算式，即

式中，α的取值会影响算法去噪效果，适当的α值能够降低噪声干扰。

最后采用交替方向乘子(Alternate Direction Method of Multiplers，ADMM)算法不断对{uk},{w k},λ进行迭代更新，直至满足终止条件，输出最终的K个IMF分量及对应中心频率。

从上述公式可以看出，参数K和α取值会对算法的分解结果产生重要影响。K值过小会导致分解不够充分，过大则容易出现虚假分量和频率重叠等问题；α值过小信号去噪不够彻底，过大则会错误去除有效成分。凭经验选取上述参数值无法确保其为最优参数。

针对此问题，笔者引入天鹰优化算法对VMD进行改进，得到最佳参数组合[K，α]。在此过程中，包络熵反映信号的稀疏性，信号中噪声越多，有效成分越少，表现为包络熵值越大；相反，信号包含有效成分越多，包络熵值越小[15]。也即当包络熵值最小时，信号包含的有效成分最多，此时对应的参数为最优。因此，笔者采用包络熵的最小值作为天鹰优化器的适应度函数，来评估参数组合的分解效果。包络熵Ep数学计算公式为

式中，m为采样点数；qp为a()q的归一化形式；a()q为经Hilbert变换后的包络信号。

1.2 天鹰优化算法原理阐述

2021年，LAITH Abualigah[16]等提出了一种新型元启发式基于种群的智能优化算法，称之为天鹰优化(Aquila Optimizer，AO)算法。与鲸鱼算法(WOA)、麻雀算法(SSA)等相比，天鹰优化(AO)算法收敛速度更快、全局搜索能力更强[17]。算法灵感源于天鹰捕猎，实现步骤为

(1) 初步确定探索范围(步骤1)

在此步骤中，天鹰在高空中垂直弯腰飞翔，搜寻猎物所在区域，初步确定最佳区域，这种行为的数学模型表达式为

式中，X1（t+ 1）为第t+ 1次迭代的解；Xbest(t) 为迭代至当前的最优解，天鹰位置适应度也最小；t为当前迭代次数；T为最大的迭代次数；XM(t) 为当前迭代的平均位置；rand 为在[0，1]区间内随机取值；N为总体的大小；Dim 为维度。

(2) 缩小探索范围(步骤2)

在此步骤中，高空飞行的天鹰确定猎物活动范围后，会在这片区域上方盘旋，随时准备落地，攻击目标。这种轮廓飞行方式目的是减小最优解的寻找空间。这种行为的数学模型表达式为

式中，X2(t+ 1)为此方法下第t+ 1次迭代的解；XR(t)为种群在[1，N]内的随机解；x，y为搜索过程中的螺旋形状；r为盘旋时的半径，r1取[1，20]；θ为盘旋角度；U，ω分别取固定值0.005 65，0.005；D1取[1，D]；Levy(D) 为莱维飞行分布函数。

式中，s，β分别取固定值0.01，1.5；u，v在[0，1]内随机取值；Γ 为伽玛函数。

(3) 扩大开发范围(步骤3)

在此步骤中，天鹰准备落地，此时天鹰会垂直下降，接近猎物对其进行试探性攻击。这种行为的数学模型表达式为

式中，X3(t+1) 为此方法下第t+1 次迭代的解；UB，LB为上下限；α，δ为开发调整参数，均取0.1。

(4) 缩小开发范围(步骤4)

在此步骤中，天鹰已接近猎物，随机飞行，攻击并捕捉猎物。这种行为的数学模型表达式为

式中，X4(t+1) 为此方法下第t+1 次迭代的解；1G为天鹰在此过程中的各种运动；2G为天鹰的飞行速率； QF（T） 为平衡搜索策略的质量函数。

基于混沌变量的随机性、有序性、遍历性等特点，为提升AO的全局搜索能力，克服其盲目性，引入Circle混沌映射确定AO的初始天鹰种群，Circle混沌映射公式[18]定义为

式中，A，B分别取固定值0.5，0.2；mod 为取余函数。

将引入Circle混沌映射后的AO命名为改进的天鹰优化(IAO)算法，图1为AO和IAO算法的寻优收敛曲线，可以直观地看到IAO算法收敛速度更快，且不易发生局部最优的现象。

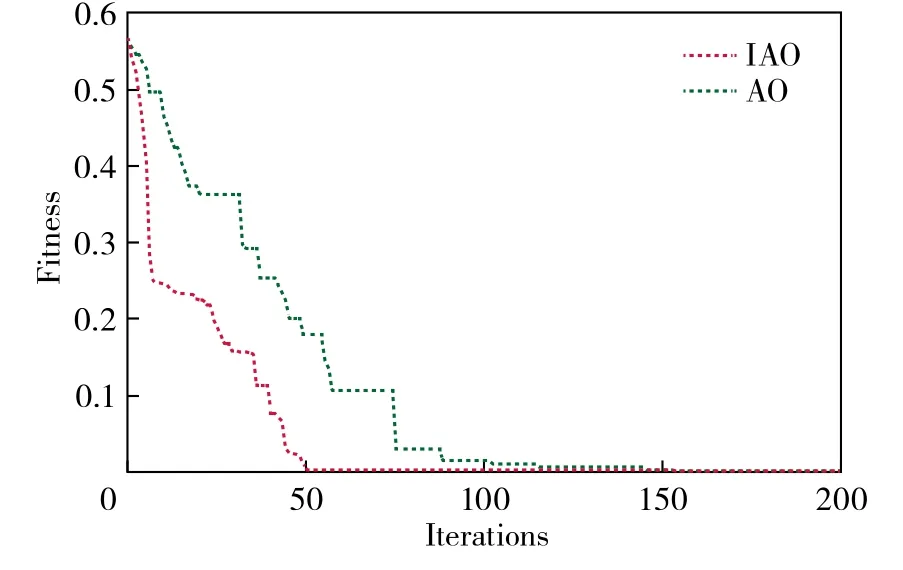
图1 AO 和IAO 的寻优收敛曲线Fig.1 Optimization convergence curves of AO and IAO

1.3 小波包分解去噪原理

小波包分解是对小波变换的改进，增加对高频信息的分解，去除高频噪声信号，可以更好地提取各个频段的有效信息，提升去噪质量。小波包分解的表达式为

式中，μ为尺度；z为位置；n为频率；为小波包分解后的子集。

式中，μ=……, -1 , 0；为第-μ层分解。

根据递推关系可以求解出小波包分解的数学模型为

式中，hz2-l，gz2-l分别为低通及高通分解滤波器。

对正交小波函数和尺度函数进行定义，得到双尺度方程为

对应的小波包重构由式(25)得到。

1.4 IAO优化VMD-小波包去噪算法

相关系数能够表征变量之间的紧密程度，数值越大，相关性越好。因此，为进一步区分出VMD分解后的含噪模态分量，笔者引入相关系数iC对其进行筛选，定义相关系数公式为

式中，iε为分解得到的各个模态分量；ϕ为原始输入信号。

IAO优化VMD-小波包去噪算法去噪流程如图2所示。

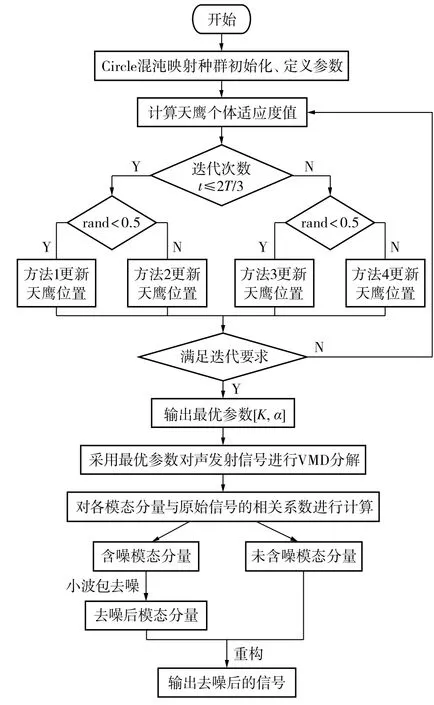
图2 IAO 优化VMD-小波包去噪算法流程Fig.2 IAO optimized VMD-wavelet packet denoising algorithm process

综上所述，IAO优化VMD-小波包去噪算法实现步骤为

(1) IAO对VMD进行参数寻优。将VMD算法的K和α两个参数作为优化目标，设定AO算法种群规模及最大迭代次数，引入Circle混沌映射初始化种群，进入迭代计算。

(2) 计算天鹰个体适应度。根据迭代条件进行判定，利用对应方法更新天鹰位置，随着迭代次数增加，天鹰个体位置不断更新，直至满足终止迭代条件后，输出最优结果[K，α]。

(3) 利用第(2)步得到的最优参数对AE信号进行VMD分解，得到K个本征模态分量。计算各模态分量与原始AE信号的相关系数，设置阈值筛选出含噪模态分量以及未含噪模态分量。

(4) 保留未含噪模态分量，并对含噪声模态分量利用小波包分解去噪。

(5) 将去噪后得到的模态分量与保留的未含噪模态分量进行合并重构，输出去噪后的声发射信号。

2 算法仿真信号分析

为了验证本文算法对AE信号降噪的普适性和有效性，在MATLAB平台上构建AE信号数学模型对其进行仿真分析。使用MITRAKOVIC D[19]等提出的随机序列，构建声发射信号的模拟数学模型。数学表达式为

式中，Qη为第η个叠加信号量的幅值；Oη为第η个叠加信号量的衰减因子；tη为叠加信号的延迟时间；fη为叠加信号的主频；F为需要叠加信号的数量。

采用式(27)对声发射信号进行仿真分析。笔者选用的仿真信号参数取值为：F= 2，Q1=Q2= 2，O1= 5.14 × 108，O2= 2.48 × 108，t1= 0.4 ms，t2=0.5 ms，f1= 80 kHz，f2= 50 kHz，信号采样频率fs设置为106Hz，模拟得到的声发射信号波形和频谱图，如图3(a)，(b)所示。

图3 模拟AE 信号及含噪AE 信号的波形及频谱图Fig.3 Waveform and spectrum diagram of analog AE signal and noisy AE signal

由于现实采集到的岩石破裂声发射信号包含诸多干扰噪声，为了使模拟AE信号更接近实测信号，笔者对模拟AE信号随机添加一组白噪声，得到含噪声发射信号的波形和频谱图，如图3(c)，(d)所示。

对模拟声发射信号运用笔者提出的算法进行降噪处理。首先，利用IAO算法来寻求对AE信号进行VMD分解所需的最优参数组合。为了更直观地验证IAO优化VMD参数的优越性，笔者采用鲸鱼算法(WOA)作为对比，两种方法均设定种群大小为30，最大迭代次数为20，迭代优化曲线绘制如图4所示。由图4可知，IAO算法在第6次迭代时已达到收敛，包络熵最小值为2.562，而WOA算法在第9次迭代时才达到收敛。结果表明，引入Circle混沌映射后的AO算法在求解速度和精度方面均表现优异。

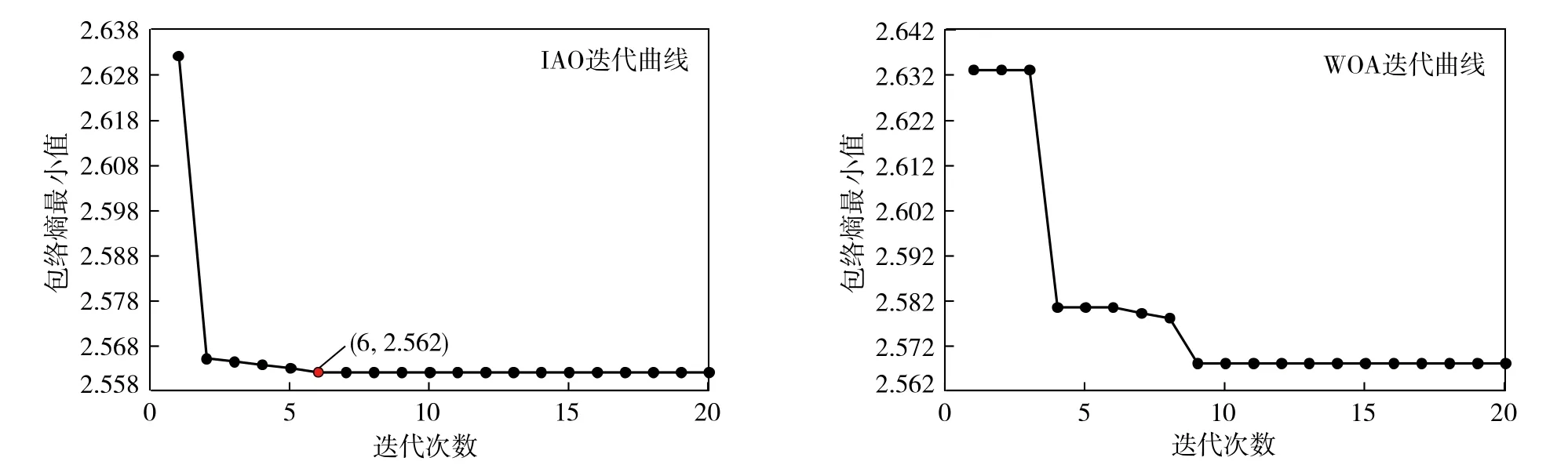
图4 IAO 和WOA 优化VMD 迭代曲线(仿真信号)Fig.4 IAO and WOA optimized VMD iteration curve(simulate signal)

经IAO优化后，MATLAB工作台得到的最优参数组合为[6，4 195]，即K=6,α=4 195。IAO算法成功解决了凭经验选取VMD算法参数非最优的问题，避免了信号有效成分的丢失，去噪更加彻底。

随后，笔者将获得的最优参数代入VMD算法对模拟含噪AE信号进行分解，各模态分量如图5所示。

图5 仿真信号的各模态分量Fig.5 Each modal component of simulate signal

由图5可知，本文算法获得的最优参数模型很好地完成了对复杂模拟信号的有效分解，经过VMD分解获得的模态分量IMF1，IMF2波形平滑且规则，IMF3～IMF6分量的波形复杂且变化较大，包含噪声较多。根据式(26)对各IMF分量与原始信号间的相关系数进行计算，结果见表1。

表1 各模态分量与原始信号的相关系数Table 1 Correlation coefficient between each modal component and the original signal

为提高相关系数在本文的适用性，考虑到不同声发射信号之间的差异性，在结合各模态分量波形图并进行多次试验验证后，拟定将相关系数大于0.5的模态分量视为优势分量(未含噪模态分量)，将相关系数小于0.5的模态分量视为需要去噪分量(含噪声模态分量)，尽可能保留原始信号完整信息，避免有效信号分量被视作噪声错误去除。

观察表1发现，IMF1，IMF2分量的相关系数均大于0.5，根据区分准则，IMF1，IMF2应被视为优势分量(未含噪声)予以保留；IMF3～IMF6分量的相关系数均小于0.5，表明其包含较多噪声成分，需要进行小波包分解降噪处理。同时，将图5的IMF1，IMF2分量波形与未含噪模拟AE信号的波形进行对比，发现二者的波形与未含噪模拟AE信号的波形较为相似，包含大量原始信号特征，应予以保留；而IMF3～IMF6分量的波形具有明显的毛刺，显然包含噪声较多。可见，通过信号波形特征进行噪声分量的区分与利用相关系数进行区分得到的结果是一致的，这进一步验证了笔者设置的相关系数筛选阈值为0.5的合理性。

综上，笔者对提出的IAO优化VMD-小波包去噪算法的模态分量区分准则进行了验证。相关研究表明，Db4(Daubechies4)小波基能够有效去除岩石声发射信号中的干扰信息，Db4小波基的紧支性和衰减性，能更好地体现AE信号的突发性和复杂性[20]。因此，利用Db4小波基函数对含噪模态分量进行分解。为了平衡信号的细节保留以及噪声抑制的效果，减少计算的复杂程度，进行了不同阈值函数以及不同层数的小波包分解对比试验验证，采用能更好保留信号特征的硬阈值函数对含噪分量进行三层分解，得到降噪后的模态分量，最后将其与保留的未含噪模态分量进行信号合成重构，输出去噪后的信号。为验证本文算法的效果，将其与小波包去噪、CEEMDAN-小波包去噪、WOA-VMD去噪等3种方法进行对比，各方法降噪后得到的波形及频谱图如图6所示。

图6 含噪模拟声发射信号不同算法去噪后的波形及频谱图Fig.6 Waveform and spectrum of simulated acoustic emission signals with noise after denoising using different algorithms

由图6可知，本文提出的算法去噪效果最好，降噪后得到的信号波形较为光滑，去除噪声的同时保留了原始信号的有效信息，较好地拟合了原始信号。其他3种算法去噪后的信号仍有一定量的噪声分量残留，毛刺较多。经CEEMDAN-小波包去噪后的信号主频部分产生了失真，最大幅值仅为1.972 V，明显低于原始信号，信号的部分有效信息被错误消除；WOA-VMD算法由于未引入小波包去噪对相关系数低于0.5的IMF分量进行处理，导致部分干扰噪声仍然残留。

另外，观察频谱图可以看出，本文算法去噪后的模拟AE信号的次、主频特征明显，完整的提取了各频次的主要特征，保留了次、主频的幅值。单纯使用小波包处理后的信号虽然去除了部分高频噪声，但并不彻底，高频部分仍存在较大波动；其他两种算法虽然也提取出了次、主频的基本特征信息，但明显可以看到信号在高频部分仍有大量噪声残留；CEEMDAN-小波包去噪后的信号未能完整保留次、主频的幅值。

声发射信号常采用信噪比(SNR)以及均方根差(RMSE)作为去噪效果评判指标，其公式为

式中，为去噪后的信号；d为信号长度。

一般认为，信噪比越大，均方根差越小，去噪效果越好。为了全面评价笔者提出算法的降噪效果，对各算法去噪结果的降噪指标进行对比，结果见表2，去噪前的模拟AE信号SNR为4.02 dB。

表2 不同算法去噪效果对比(模拟AE信号)Table 2 Comparison of denoising effects of different algorithms (analog AE signal)

由表2可知，本文算法去噪后的信号信噪比最高，均方根差最小，两种指标均优于其他3种算法。综上所述，可以认为本文提出的IAO-VMD-小波包去噪算法对声发射信号的降噪更有效，可为后续AE信号的分析提供参考。

3 岩石破裂声发射信号去噪

3.1 岩石破裂声发射试验

对单轴压缩试验进行声发射信号采集，试验采用PCI-2声发射监测系统，加载系统为WSM-200kN型微机控制岩石刚度试验机，如图7所示。

图7 声发射监测系统及微机控制加载系统Fig.7 Acoustic emission monitoring system and microcomputer controlled loading system

试验结合辽河油田某区块同一批次采集的岩体储层特点，利用工程沙、黏土、石英砂等材料，根据试验需求以及式(30)的岩体脆性计算方法，按照相关比例进行配比[21]，模拟真实情况。制备了脆性矿物含量分别为0，10%，30%，50%的方形岩心样品(参考真实岩心矿物组成)，尺寸为50 mm×50 mm×50 mm。加载速率设为2 mm/min，采用4通道采集AE数据，采样频率设置为1 MHz。

式中，V为不同矿物的体积；BRIT为脆性指数；quartz为石英；carbonate rock为碳酸盐岩；clay为黏土。

试验后随机选取一条AE信号进行可视化，如图8所示。

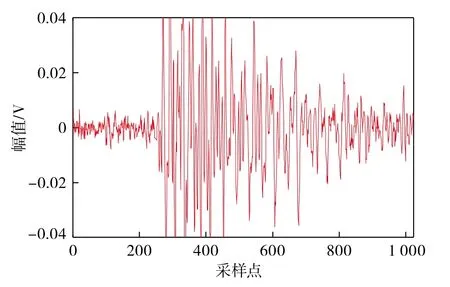
图8 选取的岩石破裂声发射信号Fig.8 Acoustic emission signal of rock fracturing

3.2 岩石破裂AE信号降噪

岩石破裂过程中产生的AE信号包含丰富的损伤演化信息，当岩体脆性矿物含量不同时，采集到的有效AE信号特征也各不相同。为方便后续探索不同脆性矿物含量下岩石AE信号的特征，构建脆性矿物含量与岩石可压性之间的关系，对采集的AE信号进行降噪处理十分必要。

由于试验加载时间较长，采集到大量AE信号，受限于篇幅无法逐一呈现信号的降噪过程及效果。笔者从4组不同脆性矿物含量(0，10%，30%，50%)的声发射信号样本库中，随机各选取了一组AE信号进行去噪分析，来对本文算法进行验证。

首先，对脆性矿物含量为0的信号采用本文算法进行降噪分析。AE信号VMD分解参数的IAO优化迭代曲线如图9所示，当迭代至第5次时，包络熵达到最小值2.894。

图9 IAO 优化VMD 迭代曲线(脆性矿物含量为0)Fig.9 IAO optimized VMD iteration curve(0 brittle mineral content)

IAO优化后得到的最优参数组合为[6，4 560]，即K= 6,α= 4 560，代入VMD算法，对实测声发射信号进行分解，得到的脆性矿物含量为0的AE信号各模态分量如图10所示。

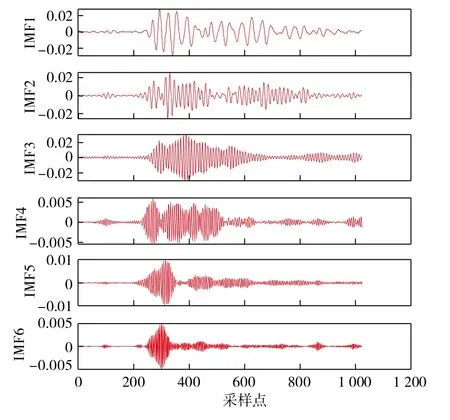
图10 脆性矿物含量为0 的AE 信号各IMF 分量Fig.10 IMF component maps of AE signals with 0 brittle mineral content

随后，对各模态分量与实测AE信号之间的相关系数进行计算，结果见表3。

表3 各模态分量与实测AE信号的相关系数Table 3 Correlation coefficient between each modal component and the actual test of AE signal

根据上文设定的相关系数筛选阈值(0.5)，对IMF1～IMF3分量进行保留，对IMF4～IMF6分量进行小波包降噪处理，之后将去噪后的IMF4～IMF6分量与保留的IMF1～IMF3分量进行合并重构，输出去噪后的信号。作为对比，笔者同时采用小波包、CEEMDAN-小波包、WOA-VMD三种算法对脆性矿物含量为0的AE信号进行去噪处理，各算法降噪后得到的波形及频谱图如图11所示。

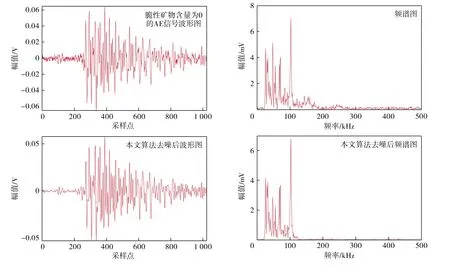
图11 脆性矿物含量为0 的AE 信号不同算法去噪后的波形及频谱图Fig.11 Waveform and spectrum of AE signal with 0 brittle mineral content after denoising using different algorithms

由图11可知，利用本文算法降噪后得到的声发射信号光滑度最高，毛刺也最少，去除噪声的同时较好地保留了原始信号的有效信息；频谱图特征明显，且与原始信号高度一致，高频噪声基本得到去除。小波包处理后的信号虽然去除了部分噪声，但频谱特征出现了较大波动；经CEEMDAN-小波包去噪后信号的低、高频部分仍有噪声残留，幅值低于原始信号，主频部分产生了失真；WOA-VMD效果相对较好，但与本文算法相比仍有少量噪声信号未能去除。

各去噪算法的降噪评价指标见表4。

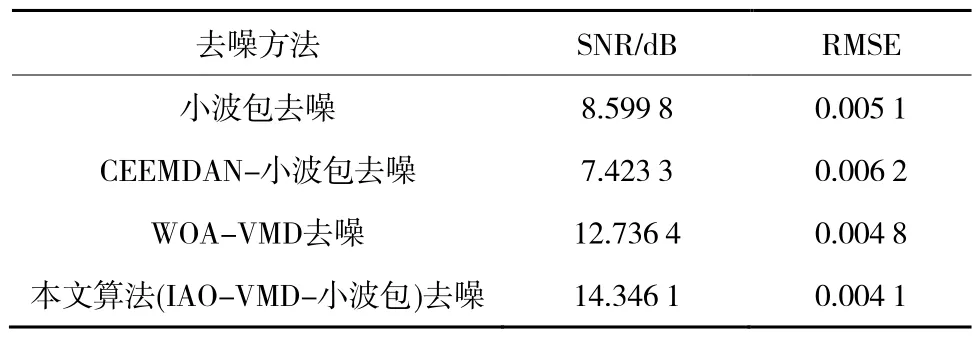
表4 不同算法去噪效果对比(脆性矿物含量为0)Table 4 Comparison of noise removal effects of different algorithms (0 brittle mineral content)

由表4可知，本文算法去噪后获得信号的SNR值最高，RMSE值最小，其在实测岩石破裂AE信号上降噪效果依旧显著，再次证明了笔者提出的去噪算法性能较好。

不同脆性矿物含量的岩石在破裂过程中产生的声发射信号特征各不相同，为验证本文算法对不同脆性矿物含量的声发射信号降噪的普适性，笔者对脆性矿物含量分别为10%，30%，50%的声发射信号进行了去噪处理，最终根据多个信号的去噪效果来进一步验证本文提出的IAO-VMD-小波包去噪算法的优越性。

随机选取脆性矿物含量分别为10%，30%，50%的AE信号，经过本文算法去噪后，得到的信号波形及频谱图如图12所示。

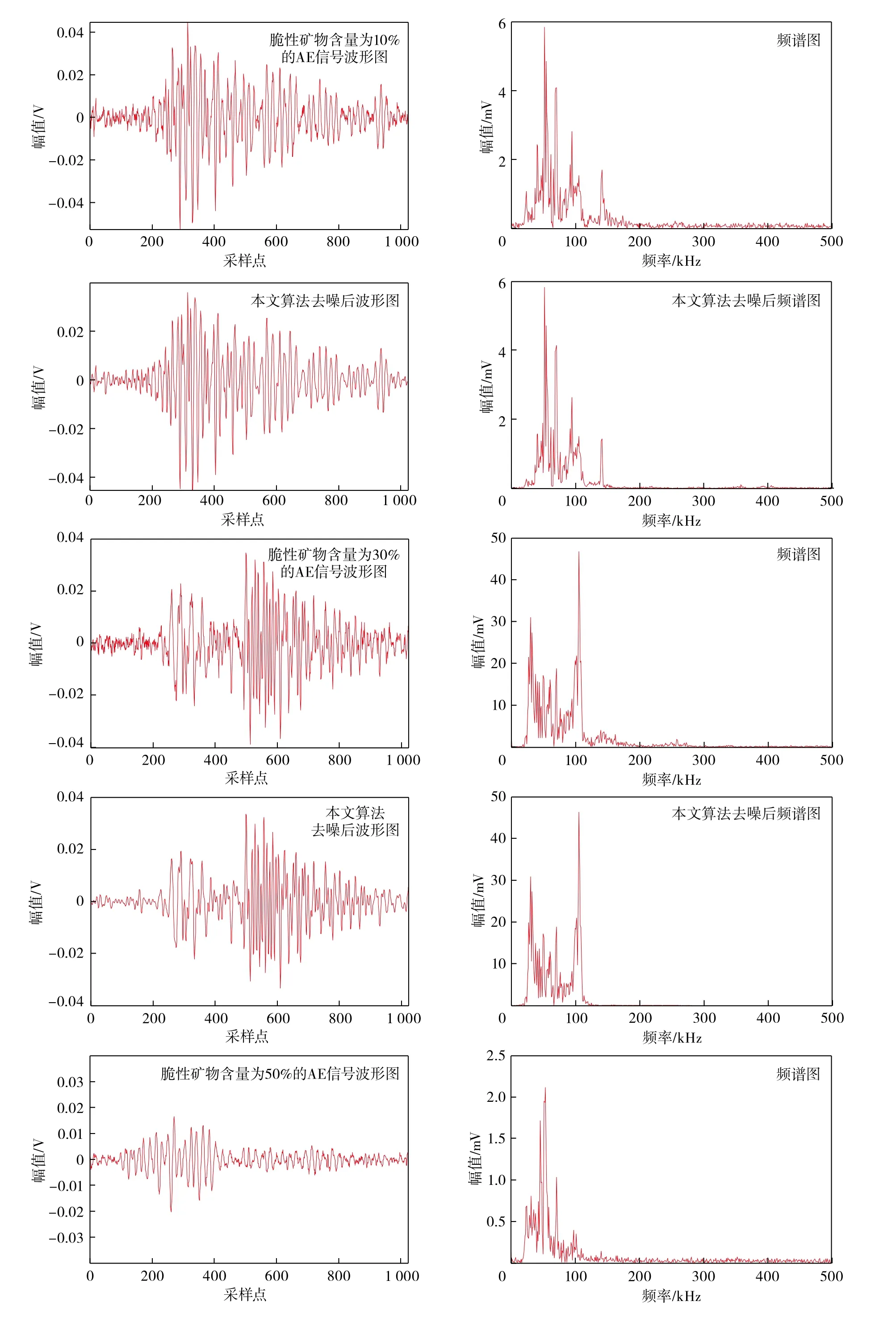
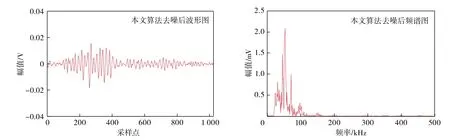
图12 不同脆性矿物含量AE 信号去噪后的波形及频谱图Fig.12 Waveform and spectrum of AE signals with different brittle mineral contents after denoising

由图12可知：基于IAO-VMD-小波包去噪算法对3组不同脆性矿物含量(10%，30%，50%)的声发射信号降噪均可取得较好效果，3组随机信号去噪后波形均较为光滑，保留了原始信号的主要特征，且未出现畸变、幅值变化等情形。各组信号的频谱特征也与原始信号高度一致，次、主频特征明显，高效地抑制了噪声干扰。

作为对比，采用不同算法(小波包、CEEMDAN-小波包、WOA-VMD)对以上3组不同脆性矿物含量的AE信号同样进行去噪，各降噪评价指标见表5。

表5 不同算法去噪效果对比(脆性矿物含量为10%，30%，50%)Table 5 Comparison of noise removal effects of different algorithms (brittle mineral content of 10%，30%，50%)

由表5可知，3组不同脆性矿物含量的AE信号经本文算法去噪后，得到的信号信噪比(SNR)均为最大，均方根差(RMSE)也均为最小，相较于其他3种算法而言，本文算法的去噪效果最好。试验结果表明，本文算法(IAO-VMD-小波包)能够较好地对各种不同脆性矿物含量的岩石破裂AE信号进行降噪处理，提取原始信号的完整有效信息，在岩石破裂声发射信号去噪方面更具优势。

4 结 论

(1) 提出一种基于改进AO的参数优化VMD算法，应用于岩石破裂AE信号的去噪过程中。在天鹰优化算法中加入Circle混沌映射，适应度函数选择包络熵最小值来对VMD算法进行参数寻优，解决了凭经验选取VMD算法参数非最优的问题。

(2) 提出IAO-VMD-小波包去噪算法，利用相关系数对各模态分量进行含噪与未含噪区分，未含噪分量予以保留，对含噪分量进行小波包去噪处理，得到去噪后的分量与保留的信号分量进行重构，输出去噪后的信号。运用仿真分析，对不同的去噪算法结果进行对比得出：IAO-VMD-小波包去噪算法降噪后的AE信号在波形、频谱图、信噪比及均方根差等方面均表现出较好的效果。

(3) 利用IAO-VMD-小波包去噪算法对不同脆性矿物含量的实测岩石破裂AE信号进行去噪处理。并与小波包、CEEMDAN-小波包和WOA-VMD算法去噪后得到结果进行对比。结果表明，该算法在保留AE信号次、主频特征的同时，高效地抑制了噪声干扰，得到的信号均具有最高的信噪比(SNR)和最小的均方根差(RMSE)，进一步证明了其在岩石破裂声发射信号去噪方面的优越性，为后续对AE信号进行准确分析提供了参考。