大断面六边形巷道周边应力分布及其支架设计

任智敏，吕梦蛟，王神虎，王 禹，张广太

(1.山西工程职业学院 采矿工程系，山西 太原 030009；2.山西潞安矿业(集团)有限责任公司 左权五里堠煤业有限公司，山西 晋中 032600)

随着井下大型机械化装备的发展，厚及特厚煤层一次采全高采煤法已被广泛应用[1]，为满足机械装备的运输、安装、通风、管线布置等要求，减少巷道上方煤损，回采巷道断面日益增大[2-3]，致使围岩破碎区半径增加，巷道稳定性降低，主要表现为整个支护系统失效及大面积冒顶、底臌、片帮等[3-5]。对于常规矩形巷道，由于应力集中，剪破裂从顶角起呈剪切滑移方式扩展，拉破裂沿主应力迹线发育，最终形成拉剪破裂网络[6-7]，导致顶角垮塌、顶板弯曲折断、煤帮大挠曲变形片帮[8-9]。由此可知，应力集中控制着巷道力学效应，是决定巷道稳定与否的根本原因之一[10]。工程实践表明弧形断面在改善巷道应力集中方面具有独特的优越性。笔者前期通过物理和数值模拟试验证实将大断面高帮矩形巷道的直边帮改造为“近似弧形”的折边帮后，巷帮的破坏程度明显降低[11-12]，此时巷道断面演化为六边形。六边形巷道的“近似弧帮”可使来自顶底板的压力沿帮传递，是一种类似压力拱的挤压结构。该结构相较于直边帮，除了可明显提升帮体承载能力外，还能在一定程度上降低帮中部的拉应力集中。故仅从围岩稳定性角度看，六边形巷道就具有理论研究价值。因此，进一步通过理论分析研究六边形巷道围岩力学特征，特别是根据应力集中来判断围岩发生破坏的潜在部位是揭示该类巷道稳定性机理的关键环节。有关折边形巷道围岩力学特性的理论解析通常采用两种方法[13]，一种是作出折边形断面的外接圆，将折边形巷道等效为圆形巷道，通过极坐标下的弹性力学理论求解；另一种是基于复变函数理论，利用解析函数的多级数展开原理建立任意孔形围岩力学分析的非迭代求解方法[14]。后者在非圆形巷道应力分布特征的表达上更为详细。

由于煤矿的地质及开采条件复杂，影响煤矿巷道围岩应力分布的因素众多。其中两类因素最为基础，一是地应力，主要由自重应力和构造应力构成，随着巷道开挖应力在围岩上重新分布，是围岩力学分析模型的基本边界条件，决定着围岩静应力分布的大小和形态[15-16]。当地应力较高时，围岩静应力可使巷道出现岩爆或持续大形变[17-18]，会极大地增加巷道的控制难度。二是采掘扰动应力，顶板活动产生的动载以应力波形式传至巷道围岩边界，在其作用下围岩产生动应力[19]。该应力与动载作用强度、扰动历时、应力波波速、围岩物性高度相关[20-21]。采掘带来的周期性扰动使得巷道围岩反复经历加卸载，在既有静应力引起的损伤基础上，交变动应力会进一步加剧围岩损伤程度和范围[22-23]。因此，研究地应力和采掘扰动应力与六边形巷道周边应力分布的变化规律对评估巷道稳定性具有重要意义。在巷道控制方面，锚杆和支架分别作为基本支护和加强支护被广泛使用，由于锚杆支护不受巷道断面形状的限制[24-25]，故六边形巷道的锚杆支护机理和方法与矩形等巷道无异，但其棚架支护则需要根据其断面形状和围岩变形量进行设计[27-28]。

综上，笔者将针对大断面回采巷道易失稳的问题，结合具体工程背景，选择六边形巷道，利用弹力复变函数理论分析巷道周边应力，确定最优巷道断面，在此基础上，分析地应力及动载对巷道的影响，并设计适于该巷道的六边形支架。研究成果将为六边形巷道围岩稳定性分析与控制提供理论参考。

1 六边形巷道周边应力分布

1.1 巷道断面轮廓映射函数

笔者以五里堠矿3号煤层地质开采条件为工程背景。工作面煤层埋深 0H=400 m，上覆岩层平均容重γ=25 kN/m3，侧压系数λ=1.5。煤层呈单斜构造，倾角1°～6°，平均厚度6.2 m，抗压强度17 MPa，弹性模量E=2.3 GPa，泊松比μ=0.3。

煤层巷道选择六边形，巷宽H、巷高B及巷帮倾角α的取值见表1。

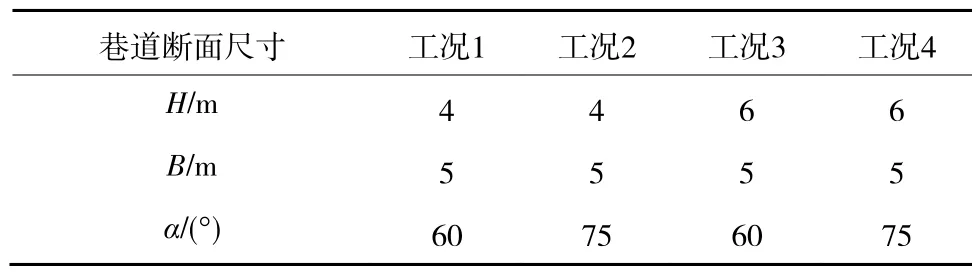
表1 六边形巷道断面几何尺寸Table 1 Geometric dimension of section of hexagon entry

对于非圆形断面巷道的应力-位移分析，可通过复变函数法求解弹性解析解。但前提是需获得表征巷道断面轮廓的映射函数，映射原理如图1所示，具体求法参照文献[29]。

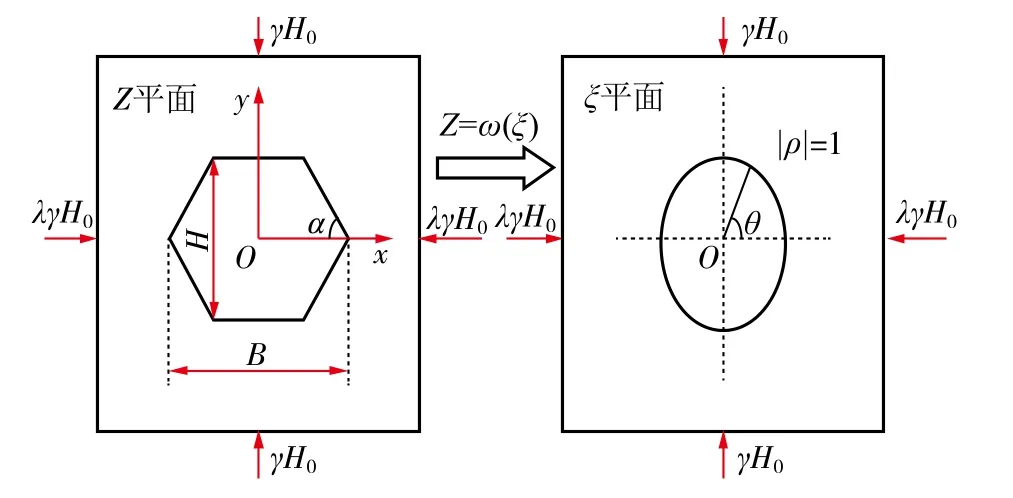
图1 巷道断面形状映射示意Fig.1 Mapping diagram of entry section shape

设由单位圆外域到巷道断面外域映射函数的级数形式为

式中，Ct=at+ ibt，t= 1, 2, ···,m。

选择(0，0)为坐标原点，则C0= 0。当Z取巷道周边上的值(x,y)时，其与对应的单位圆上的点满足：

将式(2)展开，可得巷道周边上点坐标x，y为

式中，

对式(3)～(4)进行迭代得到各工况映射函数系数，见表2。

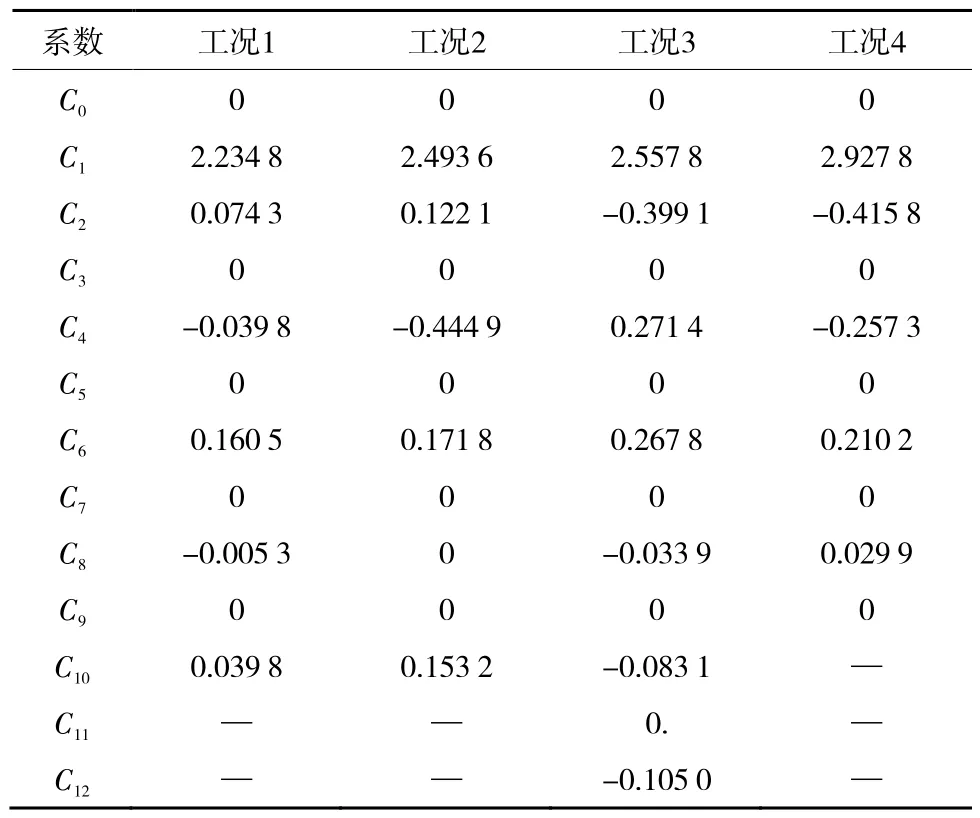
表2 映射函数系数Table 2 Coefficient table of mapping function

映射巷道断面与原巷道断面的对比如图2所示，显示两者十分接近，表明映射近似巷道断面可满足工程计算要求。

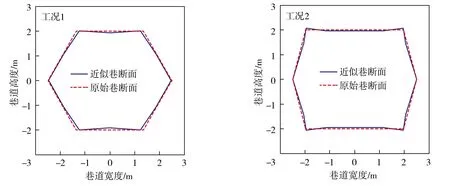
图2 原巷道形状与映射巷道形状Fig.2 Original entry shape and mapped entry shape

1.2 应力分布规律

按照平面应变问题求解巷道应力及位移。将式(1)简写成

其在巷道围岩中任意一点的水平应力σx、垂直应力σy及剪应力τ xy[30]分别为

表3和图3分别为工况1～4的巷道周边垂直应力和水平应力计算结果和分布情况。其中，拉应力为正、压应力为负。

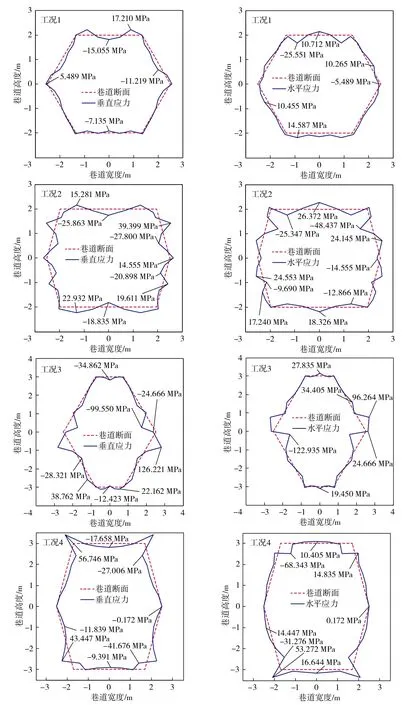
图3 巷道周边应力分布Fig.3 Stress distribution around roadway

表3 巷道周边应力计算结果Table 3 Calculation results of stress around roadway MPa

图3以分布在巷道断面轮廓线外的应力为正，以轮廓线内的应力为负。

图3显示，各工况的巷道周边应力具有相似的分布规律：

①垂直应力以压应力为主。在顶板上，压应力沿顶板中部向顶角方向呈3种分布形态：一是逐渐减小(工况3)；二是过渡成拉应力后减小(工况1，2)；三是在顶角处演变成较大拉应力(工况4)。在巷帮上，应力从顶底角向帮中方向呈两种分布：一是逐渐增大，并在帮中部出现拉压应力交替(工况1，3)；二是逐渐减小(工况4)，或是拉压应力交替的波动式减小(工况2)。

②水平应力以拉应力为主，其分布形态与垂直应力基本一致，表现为水平拉应力区即是垂直压应力区，反之亦然。

③底板应力明显小于顶板和巷帮应力。对比发现，工况1的应力值最小，应力集中程度最低，特别是其帮部垂直与水平应力集中系数仅为1.12和1.04。

工况1与工况2相比，巷帮应力分布的均匀程度显著提高；与工况3相比，其断面形状的“尖扁”度降低，轮廓曲率减小，消除了因帮中部明显转折“凸起”产生的畸高应力；与工况4相比，显著缓解了顶底角的应力集中。

说明六边形巷道在高宽比小于1且帮倾角适度时会呈现出较好的受力状态。同时考虑到煤层赋存、掘进支护、设备通行、管线布置等因素，煤矿多数巷道采用高宽比小于1的断面，结合工况1在受力方面的优势，表明宜将其作为巷道断面设计的优先选择。

1.3 最优帮倾角的确定

最优帮倾角是指最有利于围岩稳定的帮倾角，而围岩稳定性与其损伤程度密切相关，体现为围岩塑性区大小。

笔者通过数值模拟，分析帮倾角与塑性区的变化关系，从而确定其最优值。构建以工况1为背景的巷道围岩FLAC3D数值模型。巷道断面方向为x轴(取30 m)，巷道轴向为y轴(取1 m)，竖直方向为z轴(取45 m)。顶边界应力约束，左右边界x方向和前后边界y方向的速度为0，底边界x，y，z方向速度均为0，侧压系数为1.5。

笔者采用M-C模型作为巷道围岩变形破坏的本构模型，在构建模型时使用的岩层力学参数见表4。

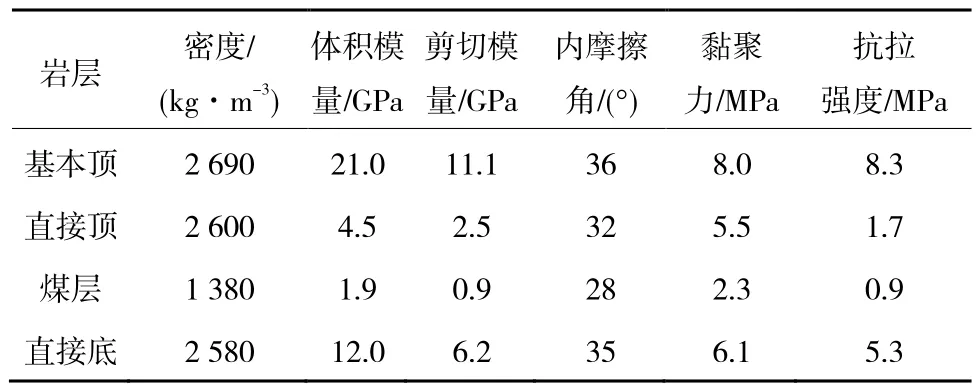
表4 岩层力学参数Table 4 Mechanical paramenters of rock stratum

计算得到帮倾角为60°，65°，70°，75°，80°时巷道围岩塑性区分布，如图4所示。由图4可知：①巷帮浅部为拉剪破坏、深部为剪切破坏，破坏深度2～3 m；顶、底板为剪切损伤，损伤深度分别为2 m和1 m，显示帮倾角对巷帮的影响最大，其次是顶板，最后为底板。此时，若支护不利，遭遇破坏的围岩将发生剥落，与已剥落围岩相邻的岩体因失去约束而发生形变，强度恶化，继而剥落，如此连锁失稳下去，直至冒落岩石充满巷道空间，破坏才会停止；②随着帮倾角增大，帮下部破坏面积首先增大，之后向下扩展至底板，随后帮上部破坏面积增加并向顶角扩展。原因是帮倾角较大时，折边巷帮趋近直边，导致其分散应力的能力显著降低，帮上应力分布的不均匀性增加，出现多个应力集中区，应力峰值向帮上、下部转移，这与1.2节工况2和工况4所示的计算结果相吻合。总体看，巷帮破坏面积在帮倾角60°时最小，约是帮倾角65°，70°，75°，80°时的75%，64%，60%，56%，此时巷道稳定性最好，故将工况1的最优帮倾角定为60°。

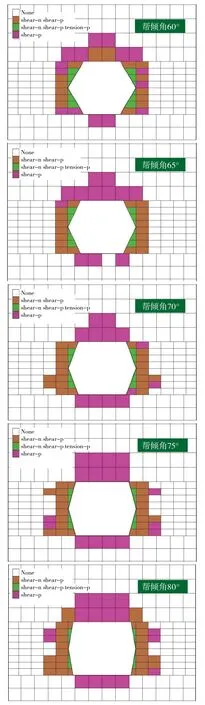
图4 不同帮倾角下的巷道围岩塑性区Fig.4 Plastic zone of surrounding rock at different slope angle of roadway-rib

2 影响巷道周边应力分布的主要因素

2.1 埋深与侧压系数的影响

在工况1基础上，通过式(5)～(7)探讨不同地应力环境下六边形巷道周边集中应力的变化规律。选择的地应力参数为：埋深400，600，800，1 000 m；侧压系数0.25，0.50，0.75，1.00，1.25，1.50，1.75，2.00。

计算结果如图5和表5所示，巷道周边集中应力(MPa)为σ=K1Hλ+K2H，K1，K2为系数。

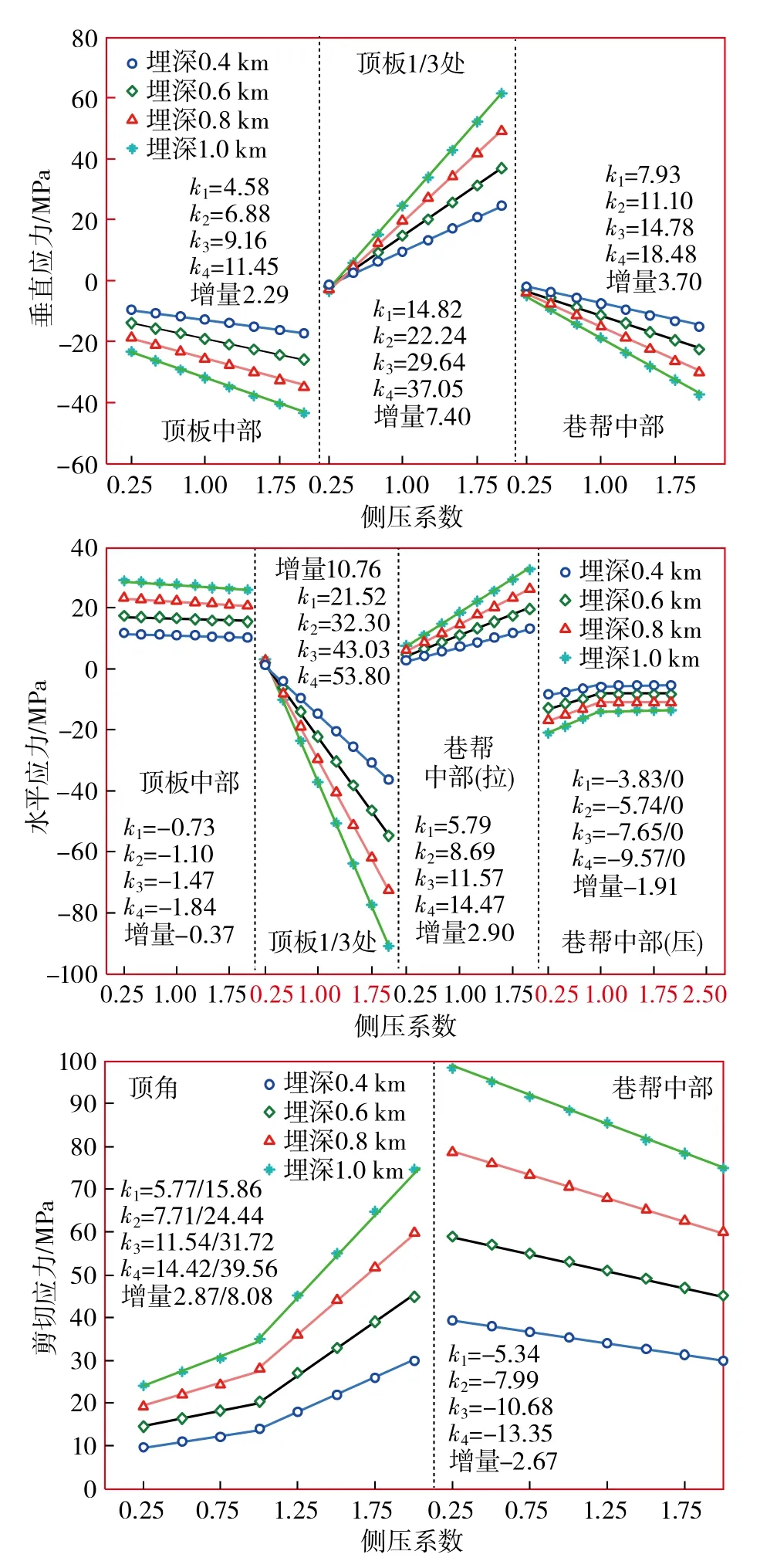
图5 埋深与侧压系数对巷道周边应力的影响Fig.5 Influence of buried depth and lateral pressure coefficient on stress around roadway

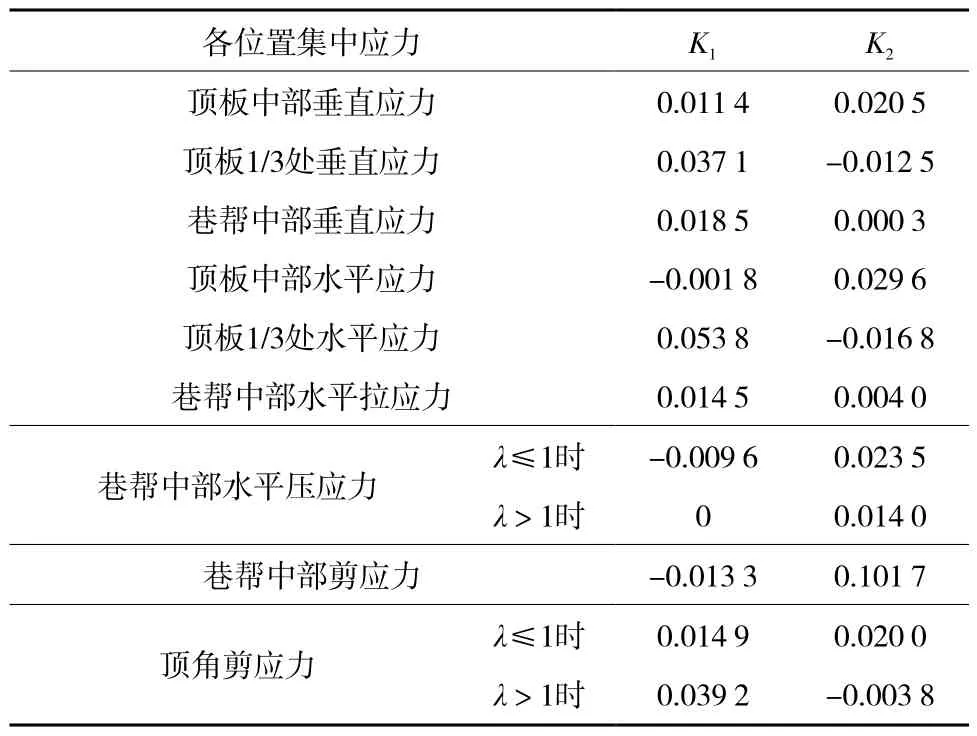
表5 巷道周边集中应力计算Table 5 Calculation table for concentrated stress

图5中k1～k4分别代表埋深为400，600，800，1 000 m时应力(σ)-侧压系数(λ)关系曲线的斜率。个别曲线斜率具有两个值，由斜杠区分，斜杠前、后数值分别表示侧压系数小于1和大于1时的曲线斜率。

埋深一定时，巷道周边应力随侧压系数增加呈线性变化，分3种形式：一是线性单增(斜率＞0)，涵盖顶板中部垂直压应力、顶板1/3处垂直拉应力和水平压应力、帮中部垂直压应力和水平拉应力；二是线性单减(斜率＜0)，包括顶板中部水平拉应力和帮中部剪应力；三是分段线性变化(斜率为双值)，主要为顶角剪应力和帮中部水平压应力，在λ＜1时两者均缓慢单增，λ＞1时前者快速增大，后者维持不变。上述说明因侧压系数增大，巷道断面不同位置应力将有增有减，但出现应力减小的位置及幅度非常有限，如，帮中部剪应力降幅约为21%，而顶板中部水平拉应力降幅较小，在浅埋深时几乎可以忽略，故整体上应力以增为主。另外，侧压系数对巷道各部位应力的影响程度不同，表现为曲线斜率越大，影响越显著。据此可知，因侧压系数改变，顶板1/3处的应力变化最大、顶板中部应力变化最小。

巷道周边应力随埋深增加呈线性增大，在图5中表现为曲线斜率的均匀增加，其又细分为两种情况：一是不论侧压系数如何变化，埋深增加引起的应力增幅基本恒定，包括顶板中部水平拉应力、帮中部水平压剪应力；二是侧压系数越大，埋深增加引起的应力增幅也越大，反之越小。表明煤矿转入深部开采后，若水平地应力较大，则顶板、顶角等处的应力会显著增大，破损风险加剧。鉴于工程背景脆性岩体的特征，仅从单一应力作用效应的角度看，巷道破坏将呈现两种类型，一类破坏是由顶板中部及巷帮中部的拉应力集中造成的，这类破坏所造成的洞形改变会使巷道周边拉应力趋向减小，故通常局限在一定范围之内；另一类破坏是由于巷道顶板、顶角及帮中部的压、剪应力集中引起的，表现为劈裂或剪切破坏，此类破坏所引起的洞形变化通常趋向于使破坏部位的压、剪应力集中程度进一步增大。所以应及时支护，有效控制围岩变形，阻止已进入塑性弱化阶段围岩强度的继续恶化，避免破坏出现累进性地加速发展，造成严重后果。

利用表4可对巷道周边重要部位应力进行预测。如，估算埋深700 m、侧压系数1.50时巷帮中部水平拉应力：

2.2 振动荷载的影响

巷道除受到地应力等静载作用外，还会受到各种动载的作用，包括采动、爆破、顶板断裂、回转下沉等引起的振动荷载。以振速作为振动荷载的强度表征，由此产生的动载荷 dσ按式(8)[31]计算，即

式中，ρ为介质密度，取1 300 kg/m3；c为振动产生的应力波波速，取3 600 m/s；v为振源振速，m/s。

选择前述的最优六边形断面，得到振速为0.36，0.48和0.60 m/s时的巷道周边应力，如图6所示。

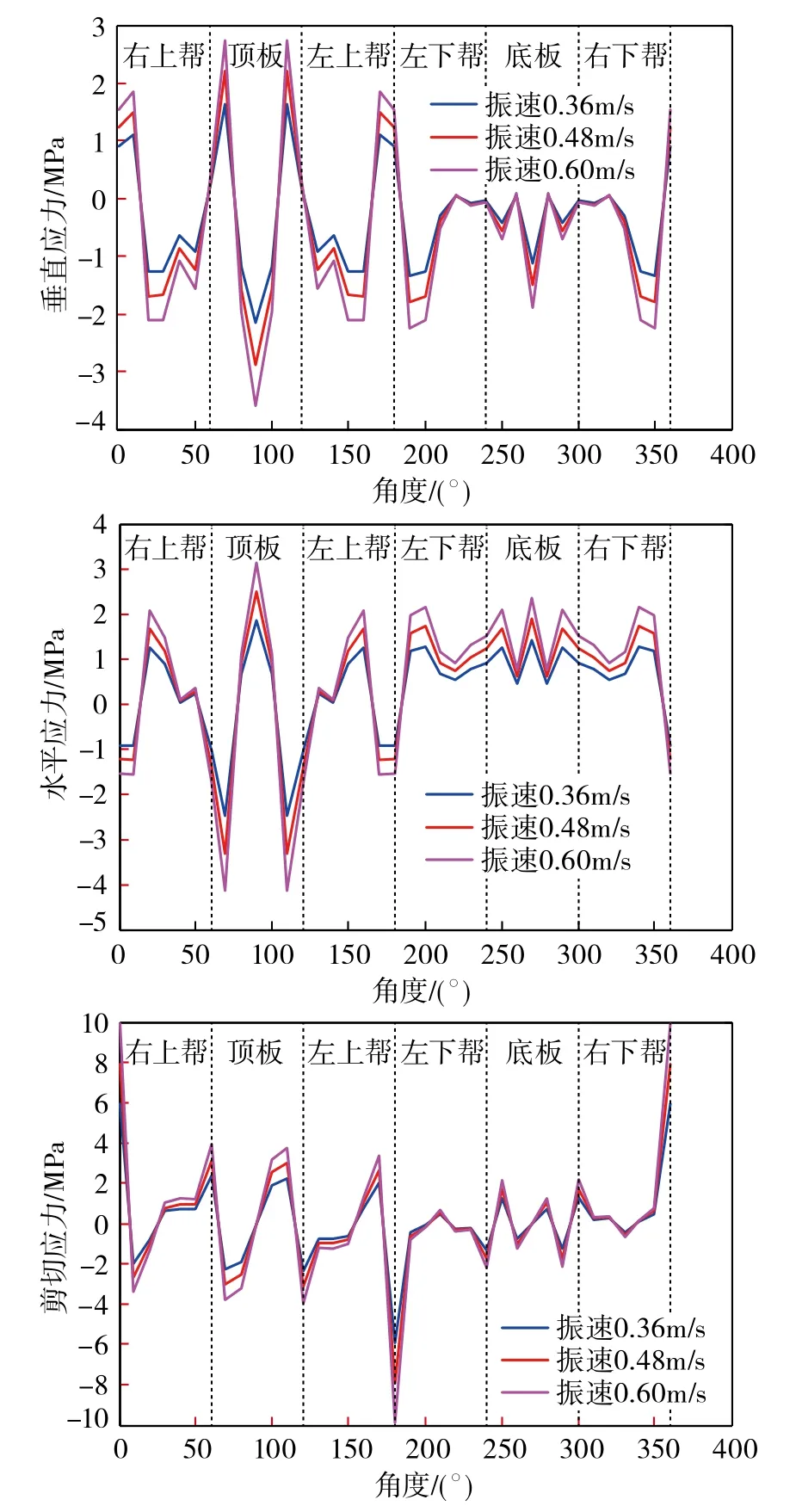
图6 振动荷载下巷道周边应力分布Fig.6 Distribution of surface stress of entry under dynamic load

模型设定围岩受到双向等压动载作用，计算结果表明动荷载下六边形巷道周边应力分布规律与静荷载下的应力分布规律基本相同，应力随振速增加而增大，但增幅因应力类型和分布位置不同而各异。垂直应力在顶底板中部、巷帮中部以及顶角的增幅最为明显；水平应力于整个巷道上的增幅均较大；剪应力增幅主要集中于顶角和帮中部。说明随着动压增加，巷道周边动应力的集中程度会显著增高。加之动-静集中应力叠加，造成围岩形变能明显积聚，从而诱发围岩冲击失稳。这解释了静压不大的巷道因一个较强扰动而突变失稳的原因。可见，为避免此类事故发生，除采取加强巷道支护、卸载降压等方式提升围岩稳定性外，降低采掘工作中各类振动强度亦是不能忽视的措施。如减慢采煤机割煤速度、减少爆破装药量、改善工作面煤壁强度或提高采煤工作面支护强度以预防顶板断裂及活动造成的矿震等。

另外，分析发现围岩各类应力对振动荷载强度的敏感程度不同，其敏感度排序依次是水平应力＞垂直应力＞剪切应力。这主要体现在动载变大时巷道底板水平拉应力会整体性显著增大，此时宜对底板增高的拉破坏风险予以一定关注。必要时可架设底拱或安装底锚。

3 六边形巷道支架设计

针对六边形巷道断面的特殊性，设计符合工程背景条件的六边形支架，对于六边形回采巷道的加强支护具有重要理论意义和实践价值。仍以工况1为例，在围岩应力作用下围岩表面发生位移，继而对约束支架产生压力，即围岩形变压力。根据该压力确定围岩支架内力、支架间距，选定支架构件材料、截面尺寸和连接方式[32]，从而设计出适应于特定开采地质条件的六边形巷道支架。

3.1 巷道围岩表面位移

巷道表面水平位移ud和垂直位移vd分别按式(9)和式(10)计算[33]。

计算结果如表6和图7所示。

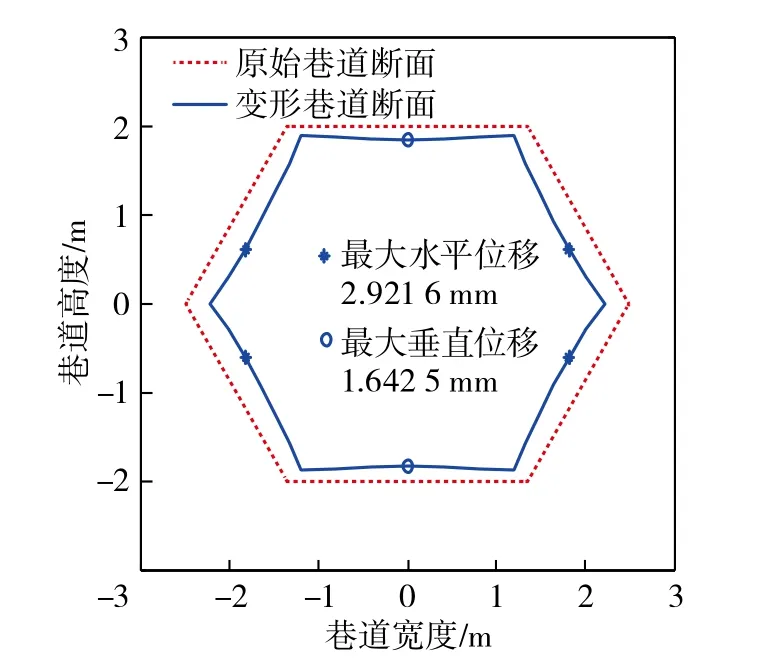
图7 巷道表面位移分布Fig.7 Distribution of surface displacement of entry

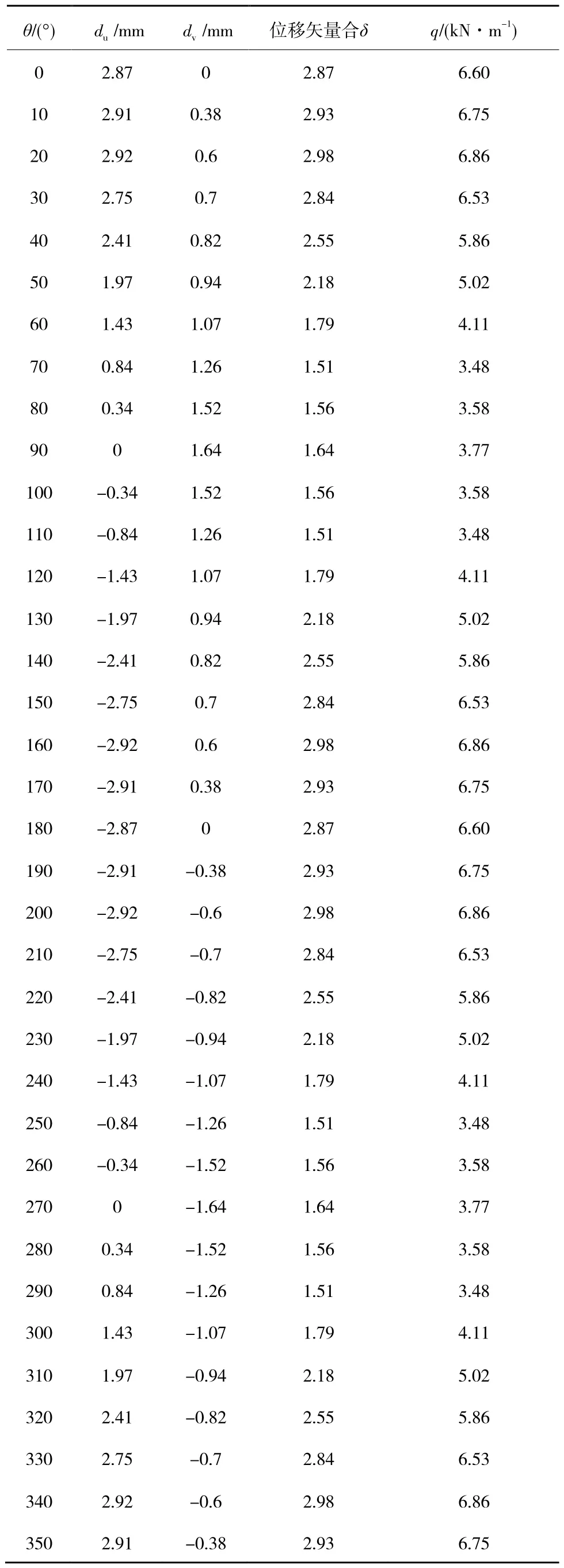
表6 巷道表面位移与支架外载计算结果Table 6 Calculation results of entry surface displacement and support external load

图7中巷道表面位移为水平和垂直位移矢量合δ。对于顶、底板，位移在其中部最大并沿两侧逐渐减小，至顶、底角处又略有增大；对于巷帮，位移在帮中部最大，沿上、下帮逐渐减小。帮部平均位移是顶、底板平均位移的1.68倍，占巷道表面位移的64.04%，说明巷道的收敛量主要来源于巷帮位移。但不论巷帮还是顶、底板，其位移量均很小，在工程容许范围内，印证了折边帮巷道较好的抗变形能力。

3.2 支架受力分析

支架所受外载(围岩压力)为均布荷载，计算公式为

式中，k为弹性抗力系数，取 4.6 ×103kN/m3；δ为巷道表面合位移，m；a为架间距，取0.5 m。

q计算结果见表6，并对其进行数据拟合，得到支架各构件的外载表达式。其中，架顶梁：

上帮架腿：

下帮架腿：

式中，x为以节点C，B，A为起点的各构件上任意一点的位置。

支架均布荷载分布如图8(a)所示。

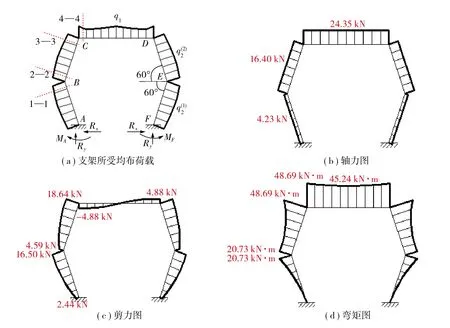
图8 支架外载及内力分布Fig.8 External load and internal force distribution of support

由以上分析可知，支架顶梁长l1=2.69m，上(下)帮架腿长l2=2.31m，q1和q2的等效集中力F1=9.77kN，F2= 14.06kN，F2至点B的距离d2=1.07m，帮倾角α= 60°。视支架为整体，通过∑Fy= 0，∑Fx= 0，∑M= 0，可计算出架与底板固定端的受力为

以各构件为研究对象，将其受力按截面的垂直与平行两方向分解，利用静力平衡条件，得节点两侧截面的轴力N、剪力Q和弯矩M，其中内力下标为截面编号。

进一步求得支架顶梁内力为

上帮架腿内力为

下帮架腿内力为

可知，支架各构件最大内力所在位置分别为顶梁4—4截面：轴力为24.35 kN、剪力为4.88 kN、弯矩为48.69 kN·m；上 帮架 腿3—3 截 面：轴 力 为16.40 kN、剪力为18.64 kN、弯矩为48.69 kN·m；下帮架腿1—1截面：轴力为4.23 kN、剪力为16.50 kN、弯矩为20.73 kN·m。因此，梁腿节点、上下帮架腿节点是支架最容易发生破坏的部位，即支架选型时强度校核的关键部位。

3.3 支架构件及其连接设计

选择支架构件型号为25b的热轧工字钢，其截面如图9(a)所示，参数见表7。依据关键部位内力计算其截面最大剪应力τmax、最大拉应力σtmax、最大压应力σcmax，计算结果见表8。由于工字钢材质为碳素结构钢Q235，其抗拉、抗压强度f=215MPa，抗剪强度fv= 125MPa，支架最大应力小于强度，表明型钢选择符合设计要求。

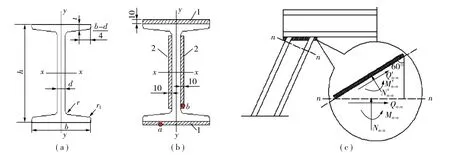
图9 支架截面与节点焊接示意Fig.9 Schematic diagram of support section and node welding

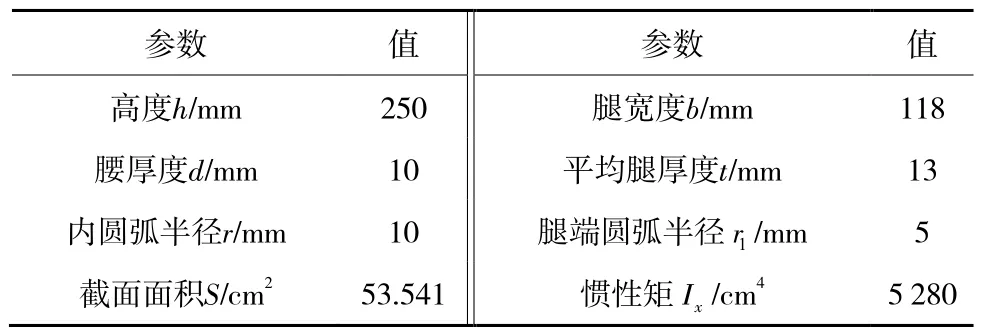
表7 工字钢支架截面参数Table 7 Section parameters of I-steel support

表8 支架构件最大应力Table 8 Maximum stress of support member MPa

支架节点处的构件采用直角焊缝连接。焊缝在工字钢截面上的布置如图9(b)所示，其中焊缝1为端缝，焊缝2则既是端缝又是侧缝，两者的有效截面积分别为Af= 4 7 88mm2和Af′=3 136 mm2。焊脚尺寸hf= 10mm，焊缝惯性矩Ix′ = 5.86 × 107mm4。

根据图9(c)可知，焊缝受到的压力为

剪力为

下标n—n于节点C时取3—3截面，于节点B时取1—1截面。在上述外力作用下，焊缝有效截面应力σ应满足：

其中，

式中，fβ为端焊缝强度增大系数，取1.22；fσ为端缝应力，MPa；fτ为侧缝应力，MPa；ymax为焊缝截面中心距点a或b的距离，mm；ffω为角焊缝强度设计值，Q235钢时取160 MPa。

由钢结构理论知，焊缝1和2的最大应力值分别位于点a和b。通过式(39)～(41)计算得a，b两点在节点C的应力为105.49 MPa和88.36 MPa；在节点B的应力为44.30 MPa和38.76 MPa。可见，上述应力均小于160 MPa，表明焊缝参数设计满足工程要求。

4 结 论

(1) 建立了基于复变函数理论的六边形巷道围岩力学模型，揭示了巷道周边垂直、水平及剪切应力分布规律。对比分析不同帮倾角下巷道围岩塑性区演化特征，发现高宽比为0.8的六边形巷道的最优帮倾角为60°。

(2) 获得了最优断面六边形巷道周边集中应力与侧压系数及采深的变化曲线，给出了不同地应力环境中巷道关键部位应力的估算表达式。分析了巷道动应力随振源振速增加的变化规律，发现动-静应力叠加明显加剧了围岩应力的集中程度，成为动压巷道失稳的诱因。

(3) 揭示了六边形巷道表面位移分布规律，获得了围岩压力函数。计算了六边形支架内力，显示梁-腿、上腿-下腿节点是支架受力最大的部位，据此确定了支架型材、支架截面形状与尺寸、节点焊接方式、焊缝参数。通过强度校验证明支架设计满足工程要求。