深井矩形巷道围岩应力分布规律及支护优化

杨 宁，赵美霞，黄玉兵

(1.江苏建筑职业技术学院 建筑建造学院，江苏 徐州 221116；2.江苏建筑节能与建造技术协同创新中心，江苏 徐州 221116；3.中国矿业大学(北京) 深部岩土力学与地下工程国家重点实验室，北京 100083)

受所处的地应力环境、服务年限、地质条件等因素的影响，我国的巷道断面形状以圆形、矩形、梯形、拱形、直墙半圆拱形等[1]为主。矩形巷道在开挖、支护方面具有快速、简便的优势，且断面利用率高，但矩形巷道易产生应力集中，承载能力和稳定性较差，因此多被用于服务年限相对较短的回采巷道[2-3]。传统求解方法很难得到精确的矩形巷道应力解析解[4]，特别是大埋深矩形巷道，其围岩应力分布更复杂，巷道稳定性控制更加困难[5-6]。

在矩形巷道围岩应力分布方面，国内外学者[7-9]通过理论计算、数值模拟等手段取得了一系列重要的研究成果。MUSKHELISHVILI[10]提出了通过复变函数法求解非圆形孔口弹性问题的基本原理与一般解法；施高萍[11]等利用复变函数分析法和映射函数法，计算了不同侧压系数和跨高比下矩形孔口的应力值，并得到了两种影响系数对孔边应力分布的影响规律；赵凯[12]等采用多角形法进行矩形巷道的映射函数逼近，并采用复变函数解法得到了巷道围岩周边应力的分布及变化规律；李廷春[13]等利用FLAC3D有限差分软件中的Cvisc模型，模拟了矩形巷道的变形破坏过程，结合现场监测结果，得到了巷道各部位的破坏模式。在巷道的稳定性控制方面，范子儀[14]等研究了不同煤柱尺寸下采动巷道围岩塑性区分布形态及应力分布特征，提出了“提升支护层次、优化大变形区域支护”为核心的支护方案；郭平[15]等在优化巷道断面基础上提出了3种巷道支护方案，并采用数值模拟方法对各方案的可靠性进行对比分析，获得了优化支护方案；王志[16]等提出一种端部扩孔锚固方法，并通过理论模型及数值计算，分析了端部扩孔锚固界面应力分布、脱锚长度扩展及端面挤压应力分布，研究了不同锚固方式巷道围岩变形、应力集中特征；谢龙[17]等采用理论分析、数值模拟等研究方法，对寸草塔二矿31204工作面回采巷道超前锚索支护的注浆压力、注浆时间及注浆间排距等参数进行了优化设计；王琦[18]等基于现场锚注扩散试验和数值模拟，提出深部巷道锚注支护设计方法；陈定超[19]等采用现场调研、数值模拟和工业性试验等手段，揭示了巷道断面尺寸效应和构造应力强弱效应对大断面巷道围岩灾变的诱导机理，提出了以“顶板强压支护+两帮注浆加固+底角锚注阻隔”为核心技术的巷道围岩稳定控制对策；张懿[20]等结合具体工程背景分析厚煤切顶巷道顶板采动失稳特征，提出了以单体液压支柱支护为承载结构的厚煤切顶巷道顶板支护控制对策，并构建了单体支柱顶板承载力学模型；李国锋[21]等采用FLAC3D软件建立了粗糙锚固结构面数值模型开展剪切试验，并对锚固系统的剪切特性以及受力变形和破坏特征进行了系统研究；刘兵晨[22]等基于岩层控制关键层理论，分析了综放工作面沿空留巷上覆岩层结构特征，获得上覆岩层活动规律。

上述研究成果丰富了矩形巷道围岩应力求解和分析手段，针对的多是稳定围岩的应力分布和演化规律，控制手段多为加强锚杆(索)支护或围岩注浆。随着煤炭开采向深部发展，工程地质条件多变，泥岩段分布广泛，围岩大变形灾害频发，因此，深井巷道围岩应力分布规律和稳定性控制仍有待进一步研究。

基于此，笔者以赵楼煤矿5302工作面轨道巷为工程背景，基于复变函数理论分析矩形巷道围岩应力，分析不同埋深、不同宽高比、不同围岩条件下巷道围岩应力分布特征，对巷道帮部不同深度围岩进行稳定性分析，从改善围岩力学性质和优化支护参数两方面提出巷道支护优化方案，并开展数值和现场试验验证。

1 围岩应力分析模型的建立

1.1 工程背景

赵楼煤矿位于山东省巨野煤田，该矿5302工作面位于五采区中部，平均埋深856.7 m。最大水平应力约为34 MPa，约为垂直应力的1.36倍。西边与未开采的5303工作面相邻，东边与已开采的5301工作面相邻，如图1所示。轨道巷顶底板岩层以粉细砂岩、细砂岩和泥岩为主，其中泥岩层岩体裂隙发育，结构松散，整体强度低。

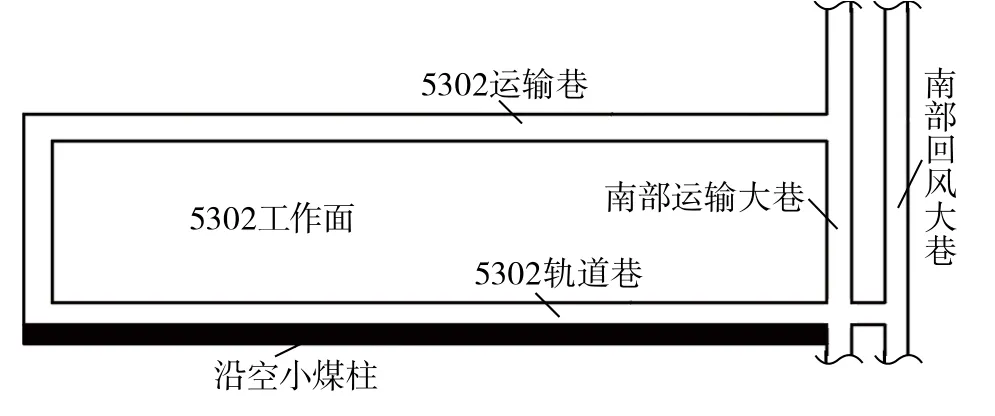
图1 5302工作面巷道平面图Fig.1 Plane figure of 5302 working face

5302工作面轨道巷为矩形巷道，该巷道净宽和净高分别为4 800 mm和3 800 mm，采用锚网+锚索+钢梯的全锚支护形式。工作面回采期间，巷道变形破坏严重，破坏位置主要集中于巷道两帮和顶板肩角处，具体表现为帮部剧烈臌出、金属网撕裂、顶板肩角沉降、顶板锚杆(索)失效等，现场破坏情况如图2所示。

图2 现场破坏情况Fig.2 The filed destructiou situation

1.2 围岩应力分析模型

(1) 基本假设

巷道周边设为无限平面区域，忽略支护阻力影响，将围岩受力问题简化为平面应变问题。

(2) 模型建立

矩形巷道周边围岩在开挖之后，其围岩应力会重新分布。建立的力学计算模型如图3所示，其中q1为水平外力，q2为垂直外力，设矩形巷道的宽度和高度分别为a和b。

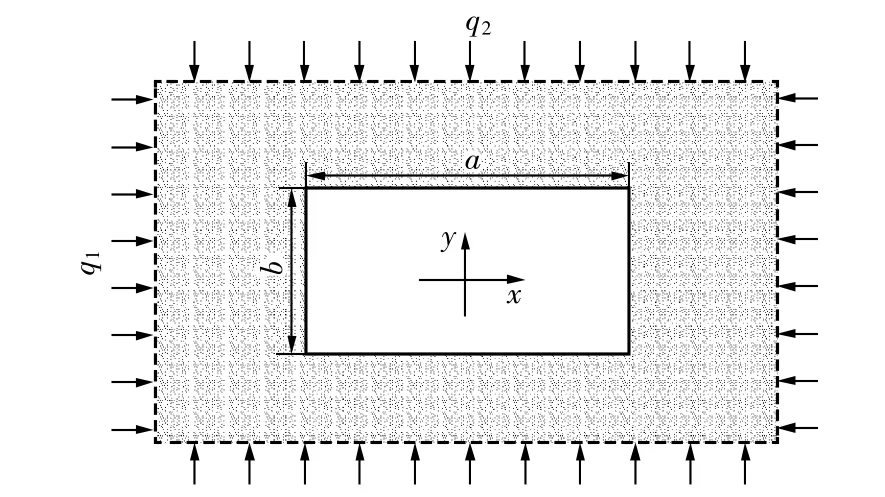
图3 矩形巷道围岩应力简化力学模型Fig.3 Simplified mechanical model of surrounding rock stress in rectangular roadway

(3) 围岩应力分析模型

利用复变函数理论[23]和保角变换方法[12,24]，通过映射函数Z=ω(ζ)将矩形巷道在Z平面上所占区域变换为ζ平面上的中心单位圆进行围岩应力的计算，如图4所示，从而推导出矩形巷道围岩在弹性状态下的应力解。

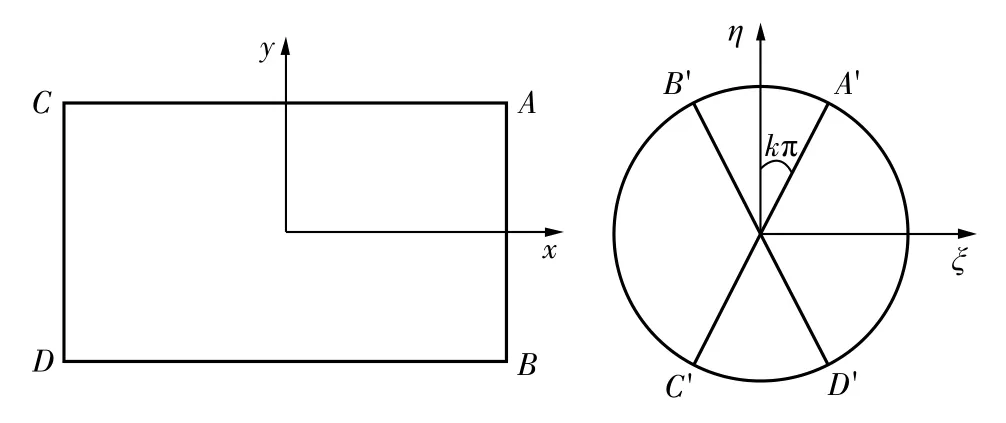
图4 矩形平面Z到单位圆ζ平面的映射Fig.4 Mapping from rectangular plane Z to unit circle ζ plane

计算过程中，将Z平面上矩形巷道各点映射到ζ平面上中心单位圆内[12]，仅取前3项进行计算，则

式中，β为复数，R为实数，与矩形巷道宽高比c有关。

针对矩形巷道的平面应变问题，首先对φ(ζ)和ψ(ζ)两个复势解析函数进行求解，进而通过以上两个解析函数表达巷道围岩应力，求解的一般公式[13]为

式中，和分别为矩形孔口边界上x，y方向面力之和；B，B'+iC'为常数，与矩形孔口远场应力有关。为方便计算引入记号f0

式中，和分别为矩形孔口边界上沿x，y方向的分布面力。

将式(5)代入式(2)～(4)，求解得到φ(ζ)和ψ(ζ)，代入式(7)，并用式(6)求解曲线坐标中矩形孔口的围岩应力分量σθ，σρ，τρθ。

2 围岩应力分析与支护方案优化

以5302工作面为背景，取平均垂直外力q2为25 MPa和侧压系数λ为1.36，利用矩形巷道围岩应力分析模型，对不同埋深、不同宽高比、不同围岩力学参数下巷道围岩应力特征进行分析，提出优化设计方案。

2.1 围岩应力状态分析

(1) 不同埋深

固定巷道的宽度和高度分别为a=4.8 m 和b=4 m，垂直外力2q=Hγ(取γ=25 kN/m3，H为巷道埋深)。选取巷道埋深分别为700，800，900，1 000 m四组模型对巷道围岩应力分布进行分析，变化规律如图5所示。

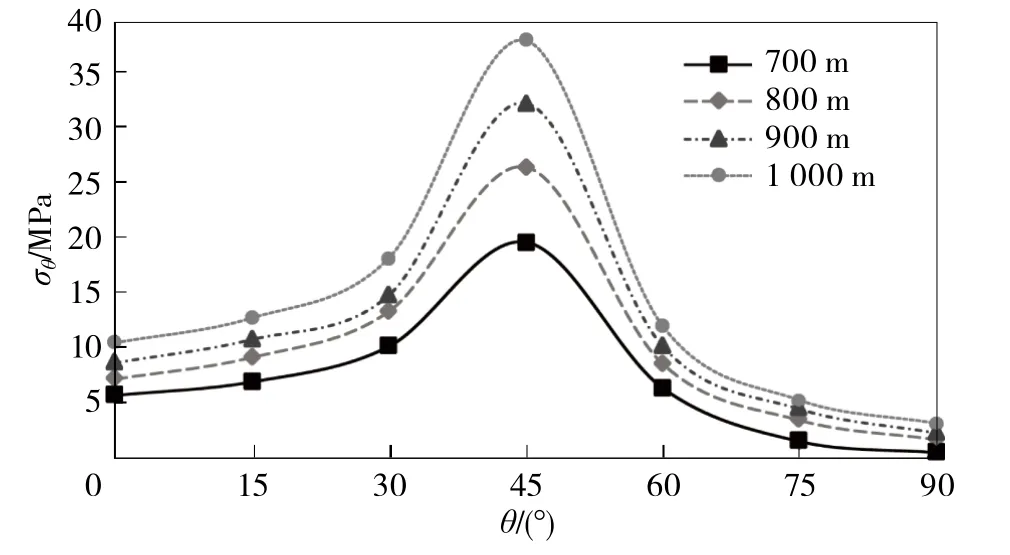
图5 不同埋深下矩形巷道围岩应力变化规律Fig.5 Stress change chart of surrounding rock of rectangular roadway under different depth of burial

由图5可知，巷道围岩应力受埋深H的影响十分显著。埋深对肩角区域的应力集中程度影响最为明显，且随埋深的增大应力值不断增大；两帮及顶底板处的应力受埋深的影响相对较小且随埋深的增大，其应力增长幅度较小。其中，巷道肩角区域的应力变化幅度最大，且同一位置的应力在不同埋深H的作用下表现为两帮的变化幅度大于顶底板的变化幅度。

(2) 不同宽高比

固定巷道高度b为4 m，选取巷道宽度a为2.8，3.6，4.0，4.8 m和5.6 m，即巷道宽高比c分别为0.7，0.9，1.0，1.2和1.4共5组计算模型。5组模型的计算系数见表1[24]，利用Matlab数学软件对前述解析式进行编辑，对每组模型的围岩应力特征进行分析，得到不同宽高比下矩形巷道围岩应力变化规律，如图6所示。

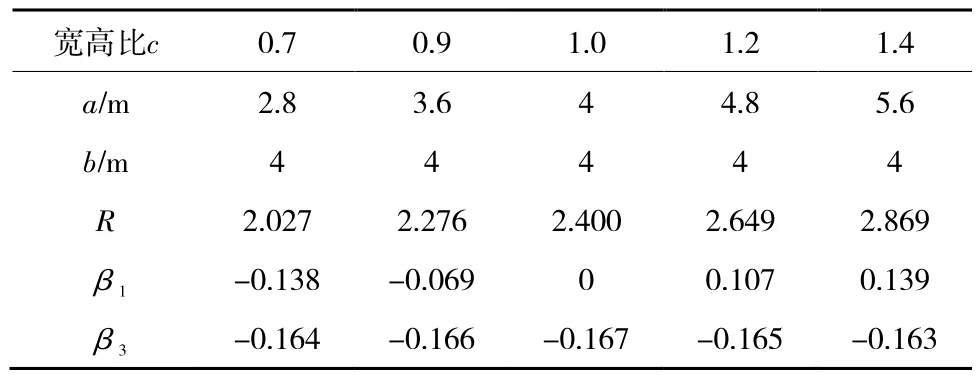
表1 不同宽高比c下保角变换参数的计算系数Table 1 Computational coefficients of conformal parameters under different width-height ratios c

图6 不同宽高比下矩形巷道围岩应力变化规律Fig.6 Stress variation pattern of surrounding rock of rectangular roadway under different width-height ratio

由图6可知，映射角度在40°～45°时应力达到最大值，说明肩角区域的围岩应力集中程度最为明显，顶底板及巷道两帮的围岩应力较小。宽高比c对矩形巷道围岩应力值和分布特征影响较小，其中帮部应力随宽高比的增大而增大，且变化幅度基本一致，但顶底板处应力随宽高比的增大而减小。当侧压系数λ固定时，肩角处应力在0＜c≤1.0时单调递增，且c=1.0时应力取到极大值，在c＞1.0时单调递减。

(3) 不同围岩参数

通过上述分析可知，不同埋深和不同宽高比下矩形巷道帮部围岩应力大于顶底板围岩应力，且现场原支护方案表现为巷道两帮变形破坏程度最大。因此，主要针对巷道帮部围岩稳定状态进行分析，选取巷道帮部θ=0°这条映射路径，通过式(8)[25]，作此映射路径上不同内摩擦角和黏聚力条件下的围岩稳定性系数分布曲线，如图7所示。分析巷道帮部围岩的稳定性，其中，稳定性系数为负值时表明巷道围岩处于安全状态。

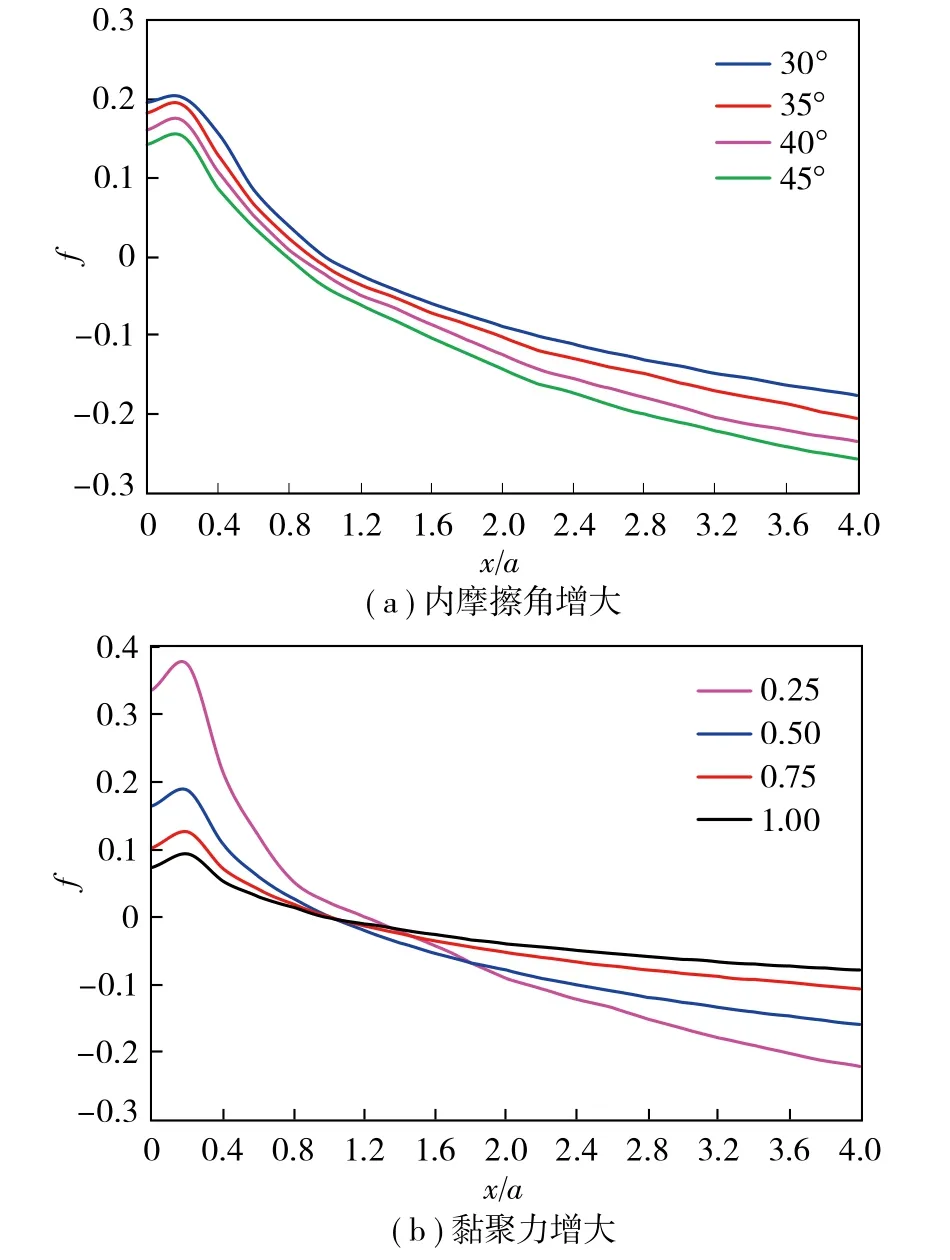
图7 不同围岩参数下稳定性系数随巷道表面距离变化曲线Fig.7 Curves of risk factors with distance from the roadway surface under different surrounding rock parameters

式中，f(ρ, ,θ φ）为围岩稳定性系数；φ为岩体内摩擦角；1σ为最大主应力，MPa；3σ为最小主应力，MPa。

由图7可知：①随着围岩内摩擦角的增大，巷道同一位置处，稳定性系数逐渐降低并趋于负值，围岩由外向内快速趋于稳定状态。说明内摩擦角增大一定程度上可以提高围岩的承载能力，从而降低巷道围岩失稳破裂的可能性。②黏聚力由0.25增大至0.50时，围岩稳定性系数下降最多，且很快趋于负值，但黏聚力增大至0.75和1.00时，其稳定性系数曲线变化趋势与0.50时相差不大，说明对某一岩体，在一定物理力学参数范围内提高黏聚力可有效提高其稳定性，但超出范围后提升能力有限，且弱于内摩擦角。综上，在一定范围内提高围岩力学参数可有效降低帮部围岩稳定性系数，提升巷道整体稳定性。

2.2 矩形巷道支护方案优化

由巷道围岩应力特征及帮部围岩稳定性分析可知，矩形巷道肩角区域的围岩应力集中程度最为明显，提高围岩参数对围岩整体稳定性及承载能力有一定促进作用。因此，从优化锚杆支护参数和提高围岩力学性质两方面对巷道尤其是帮部围岩进行支护优化。

(1) 锚杆参数设计

巷帮作为顶板承载基础，是巷道围岩承载结构中竖向荷载的主要承载者，减小巷道围岩竖向荷载能够有效控制煤帮变形。

针对破碎围岩，通过悬吊理论确定锚杆的长度，即

式中，l为锚杆设计长度，m；l1为锚杆锚固长度，m，l1=nh0，n为安全系数，h0为冒落拱高度；l2为锚杆有效长度，m；l3为锚杆外露长度，m。

为保证支护过程中锚杆的可靠性，其有效长度应大于冒落拱高度，即l2≥h0。

巷道开挖后，应力重新分布导致围岩不断破碎，形成以巷道为中心的冒落拱[26]，并在围压作用下不断扩大。基于极限平衡原理和普氏理论，且考虑到计算结果的可靠性，利用式(10)对锚杆参数进行优化。

式中，A为巷道宽度的1/2，m；b为巷道高度，m；fφ为岩体的内摩擦角；f为顶板岩层的普氏系数；m为安全系数，一般取1.5～2.0。

(2) 围岩力学参数

研究表明注浆能够提高围岩力学参数和巷道稳定性。原支护方案仅采用锚杆(索)加固巷道，未对巷道进行注浆加固。在优化方案中，选用中空注浆螺纹锚杆，以水泥单浆液为主，水灰比为0.5∶1，同时加入质量为水泥用量1.5%的减水剂，注浆压力控制在2～3 MPa。

参考已有研究中关于破碎煤岩体注浆加固试验及注浆后参数的选取方法[27-30]，煤岩体在注浆加固后弹性模量、黏聚力、抗拉强度变为原来的1.5～2.0倍，内摩擦角增加3°～5°，泊松比减小0.02～0.05。考虑到实际注浆加固的效果，其有效加固区内各围岩参数均取较小值，具体见表2。

表2 5302工作面矩形巷道地层围岩参数Table 2 Mechanical parameters of surrounding rock in stratum of rectangular roadway in 5302 working face

(3) 优化方案设计

① 原支护方案

顶板锚杆为ϕ22 mm×2 500 mm的KMG500高强左旋无纵筋螺纹钢锚杆，间排距850 mm× 800 mm；顶板锚索为ϕ22 mm×6 200 mm高强低松弛预应力钢绞线及配套锁具，间排距1 700 mm× 1 600 mm。

帮部采用ϕ22 mm×2 500 mm的KMG400左旋无纵筋全螺纹锚杆，间排距800 mm×800 mm；实体煤侧及沿空侧帮部设置的锚索直径22 mm，排距设置为1 600 mm，长度为6.2，3.5 m，原支护方案见图8。

图8 原支护方案Fig.8 Initial supporting plan

② 优化方案

基于对锚杆参数设计和围岩参数的改善分析，结合现场实际地层条件和施工情况，提出以下优化方案：两帮采用ϕ22 mm×3 000 mm的注浆锚杆进行注浆加固，间排距为1 600 mm×1 600 mm，浆液水灰比为0.5∶1，注浆压力不超过3 MPa；顶板锚杆改用ϕ22 mm×3 000 mm的高强螺纹锚杆，顶板其他支护参数与原方案一致，帮部注浆锚杆补强方案如图9所示。

3 支护效果数值模拟分析

为了验证优化方案的控制效果，利用FLAC3D有限差分软件对原支护方案和优化方案进行模拟，以指导现场矩形巷道支护方案设计。

(1) 模型建立建立如图10所示的巷道模型。依据表2中围岩参数对各地层赋值，按平面应变问题进行分析。对锚固加固区进行模拟优化时，依据现场锚注试验的注浆加固范围[31]，参考文献[32-34]的研究成果，设置两侧有效加固范围为1.20 m。

(2) 围岩应力对比分析

原方案与优化方案下巷道围岩的最大、最小主应力模拟结果，如图11和图12所示。

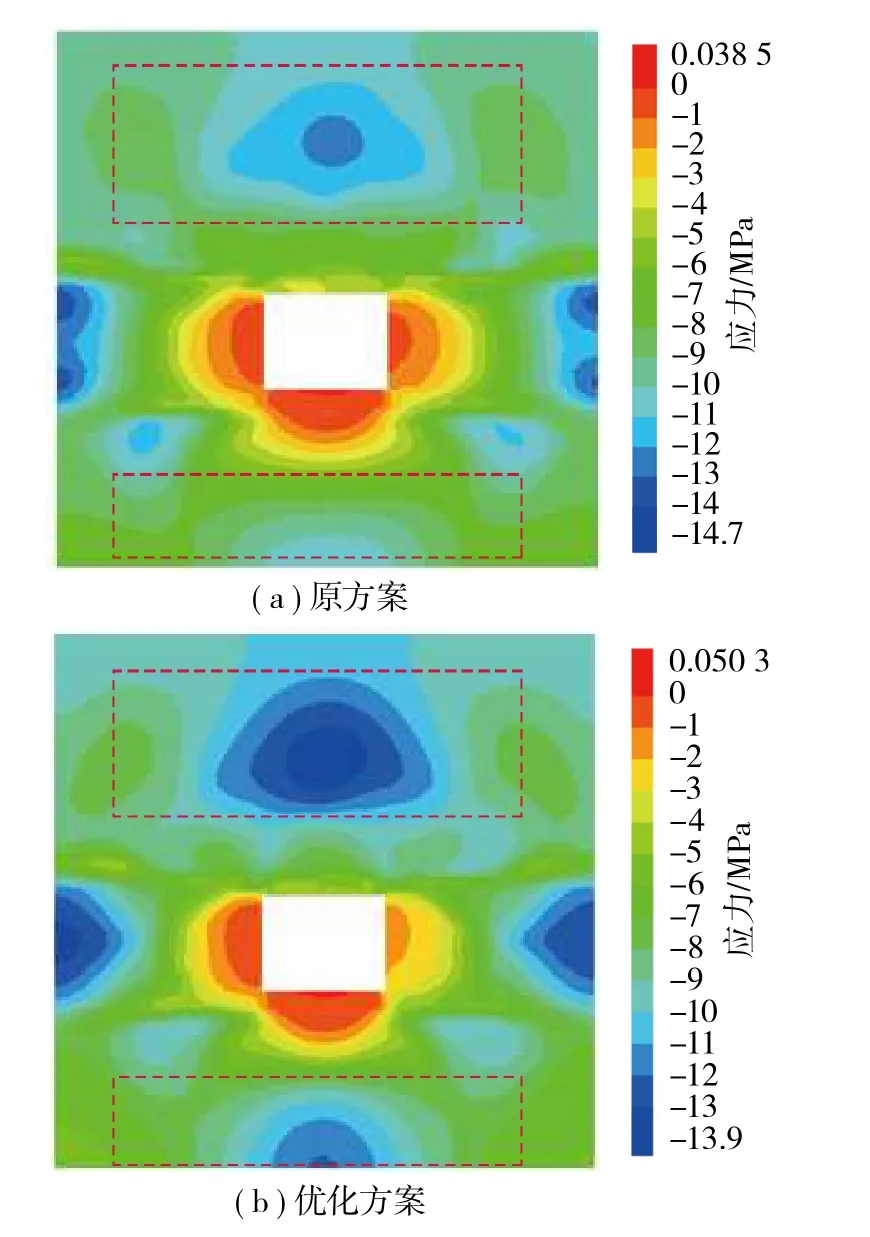
图12 最小主应力结果Fig.12 Comparison diagram of minimum principal stress

由图11和图12可知，矩形巷道4个肩角区域的围岩有明显的压应力集中现象。相较于原支护方案，可以观察到随着优化方案支护强度的提高，围岩应力集中区逐渐靠近巷道，分布范围减小，说明注浆在一定程度上充填了破碎岩体裂隙，提高了围岩完整性，同时在巷道周边形成了有效承载结构，抑制了围岩内部应力的过度集中。

(3) 围岩变形对比分析

原方案与优化方案下巷道围岩的水平位移和垂直位移模拟结果，如图13和图14所示。

由图13和图14可知，围岩变形主要集中在巷道表面至围岩内部5.0 m内，巷道两帮变形量大于顶底板处围岩变形量。提取巷道变形最大值可知，原方案最大水平位移和垂直位移为407 mm和299 mm，优化方案最大水平和垂直位移为273 mm和204 mm，分别降低了32.9%和31.8%，控制效果显著。

4 现场试验

为进一步验证“顶板锚杆加强、巷帮注浆加固”破碎围岩条件下锚注支护参数设计的可行性，在5302轨道巷开展了现场试验，如图15所示。对巷道收敛变形进行现场监测，结果如图16所示。

图15 现场试验Fig.15 Field test

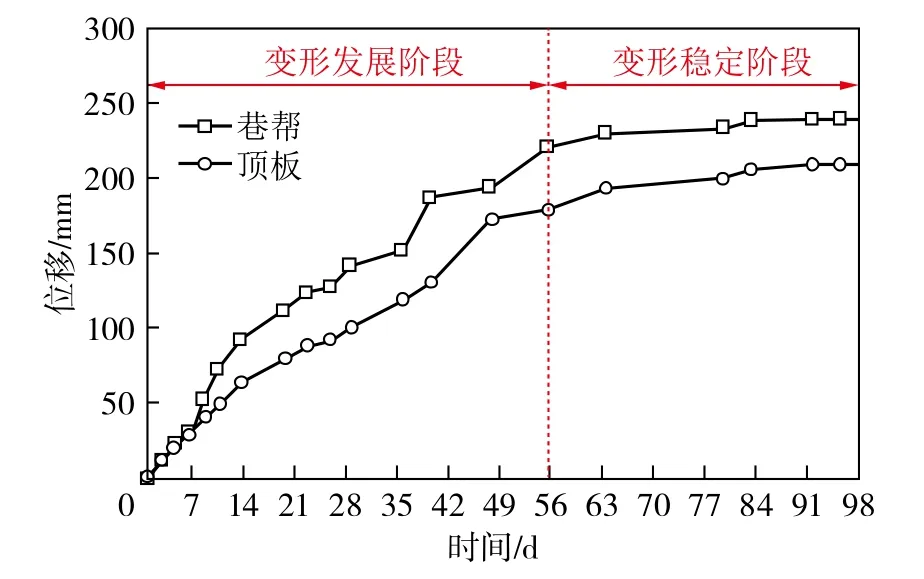
图16 巷道收敛监测曲线Fig.16 Displacement change of roadway surface

分析图16可知，巷道收敛变形在56 d左右趋于稳定，两帮变形量约2 5 6 m m，顶板沉降量约197 mm。监测数据表明，采用顶板锚杆加强、巷帮注浆加固方案有效控制了巷道围岩变形。

5 结 论

(1) 基于复变函数理论，分析了不同宽高比和埋深下矩形巷道围岩应力分布特征，结果表明：矩形巷道肩角处应力集中现象明显，应力值从大到小依次为：肩角＞两帮＞顶底板；宽高比c对巷道围岩应力的影响较小，但埋深对巷道围岩应力的影响非常显著。

(2) 对原支护方案下变形破坏最为严重的巷道帮部进行稳定性分析表明，改善围岩内摩擦角和黏聚力可以提高巷道围岩的稳定性及承载能力。基于此，从锚杆参数和围岩性质两方面进行设计优化，指导现场工程。

(3) 采用FLAC3D有限差分软件模拟了原支护方案和优化方案，对比分析了两种方案下的围岩应力和变形，数值模拟和现场监测结果表明：优化方案的巷道帮部变形比原方案降低了32.9%，控制效果明显，验证了优化方案的合理性。