一种凸多边形的爆破网络等时线算法研究
郑 武,王 磊,吕仁辉
(武汉科技大学计算机科学与技术学院,湖北武汉430081)
1 问题的提出
在爆破工程中,为了精确控制爆破过程,通常需要借助等时线来分析爆破的趋势[1],通过将起爆时刻相同或相近的炮孔用等时线连接起来,就可以更加直观地看到爆破的进度,而且可以根据等时线进一步确定整个爆破的延伸方向。在实际中,通常是先计算出每个炮孔的起爆时刻,然后统计出起爆时刻相同或相近的炮孔,最后分析爆破的趋势。某爆破项目的示意图如图1,其中数字代表起爆时刻,有箭头的线段代表孔外延时,没有箭头的曲线代表等时线,红色实心小三角形指明了爆破的岩石移动方向。CHI Bao-ming[2],ZHANG Wei[3]等学者对针对爆破网络设计中的等时线进行了相关研究和探讨。研究者们提出的等时线算法,针对布孔比较规律的情况下比较有效,但却有不同延时时间的等时线会存在交叉,获取等时线时间过长等问题[1-3]。
爆破网络等时线的生成与优化问题描述如下:在给定的爆破网络中,所有炮孔的起爆时刻已知,炮孔的位置已知,需要将起爆时刻相同(或近似相同)的炮孔用等时线连起来。要求生成的等时线至少满足4个条件:
(1)同一等时线不会自相交叉;
(2)等时线简明直观,路径较短;
(3)等时线能自动适应网络变化;
(4)等时线生成效率较高。

图1 某工程爆破网络示意图
为了更详细地说明问题,将工程爆破中的相关术语及算法问题形式化描述如下:
定义1 起爆时刻,即爆破工程中炮孔实际起爆的时刻。爆破网络给定之后,每个炮孔的起爆时刻是客观存在的。起爆时刻可以根据爆破网络中的炮孔布局计算得出。
定义2 等时线,即爆破工程中,为了准确直观地分析爆破过程,将起爆时刻相同(或近似相同)的炮孔连接起来的线。
本文通篇都涉及到等时线一词,包括等时线的定义、计算、生成、优化等,等时线的形式化定义如下:
定义 Xi、Xj为两个不同的炮孔,t(Xi)、t(Xj)是炮孔的起爆时刻,Δt是允许的时间间隔。
若│t(Xi)-t(Xj)│≤Δt,则称 Xi、Xj等时,采用等时线连接;
若│t(Xi)-t(Xj)│ > Δt,则称 Xi、Xj不等时,不用等时线连接;
其中 1≤i≤n,1≤j≤n。
严格按照前文所述的算法要求来完成算法的实现。为了避免同一等时线的交叉问题,采用凸多边形算法进行等时线的连接。为了使得生成的等时线路径较短,采用自定义三角形算法进行比较,并采用贪心算法进行优化。具体分为如下几个过程:
(1)将爆破网络中的炮孔按照起爆时刻进行分类。
(2)将同一起爆时刻段的炮孔按层次划分,主要采用凸多边形生成算法进行归类。
(3)将同一起爆时刻段上的炮孔按照上一步划分的层次,初步形成等时线。过程如下:已知最外层的凸多边形,形成一个回路。首先将次外层的凸多边形上的各个顶点插入到回路中去,插入时选取插入后使得路径最短的动作来做。然后按照从外到内的顺序依次将各个凸多边形上的顶点插入到回路中去。文中采用一种三角形方法来快速选择优先插入的炮孔。
(4)判断形成的等时线是否存在自相交叉情况,如果存在则进行去交叉算法。
(5)使用贪心算法进一步优化等时线。
2 算法描述
在实际的爆破工程中,一般会用到大量的炮孔,炮孔的位置是根据爆破的需要而分配,炮孔的起爆时刻也不全相同。在统计完炮孔的起爆时刻后,会发现同一起爆时刻的炮孔位置很散乱的分布,这时如何将各个起爆时刻相同的炮孔连成一条等时线呢?使用相邻连接的办法经常会造成连线的交叉、相邻的距离很远等缺陷,为了避免这些问题,我们需要采用一种新的等时线生成算法——基于凸多边形的插入算法。为了尽可能详细的说明这一算法,本文只讨论一条等时线的生成,基本模型如图2。给定一些均匀分布的炮孔,这些炮孔的起爆时刻相同或近似相同,每个炮孔的位置已知,要求把这些炮孔连成一条等时线。图2中所有炮孔的起爆时刻相同或近似相同,炮孔的位置是均匀随机分布的。

图2 均匀分布的100个炮孔
2.1 按层次划分炮孔
第1步 在图2所示的区域里搜索出以炮孔位置为顶点的最外层的凸多边形,标记这个凸多边形上的炮孔,并标记这个凸多边形为0层(搜索凸多边形可以参考 Graham's Scan 算法)[4];
第2步 在剩余没有被标记的炮孔中搜索以炮孔位置为顶点的最外层的凸多边形,标记这个凸多边形上的炮孔,并标记这个凸多边形为第1层。
……重复第2步的操作,直到剩余的没有标记的炮孔位置不足以构成一个凸多边形。
在执行完所有的步骤之后,原来没有规律的炮孔已经被按层次分开了,如图3。

图3 搜索所有的凸多边形
2.2 炮孔分层插入
在找到所有的凸多边形后,对这些凸多边形进行编号,从最外层到最内层依次为第0层,第1层,第2层,……,第n层(注意,如果最里面有不在凸多边形上的炮孔,那么把这些炮孔记作最内层上的,即第n层)。
插入过程如下:
第1步 将第1层上所有的炮孔依次插入到第0层,执行完之后第1层为空,第0层上新增加了原来第1层所有的炮孔;
第2步 将第2层上所有的炮孔依次插入到第0层,执行完之后第2层为空,第0层上新增加了原来第2层所有的炮孔;
……重复第2步的操作;
第n步 将第n层上所有的炮孔依次插入到第0层,执行完之后第n层为空,所有的炮孔都被添加到第0层上,即当前只有一层。
为了保证最终形成的等时线最短,没有交叉,就需要确定最优的插入算法。具体的过程是将待插入的炮孔在每个能够插入的位置进行一次插入操作,而最终选择执行完插入操作后总路径最短的插入方法,具体的插入过程分成两步。
2.2.1 插入位置选择
算法如图4。炮孔p0有两个插入位置可以选择(p1与p2之间,p2与p3之间),采用算法1之后增加的长度为Δs1=a1+b1-c1;采用算法2之后增加的长度为Δs2=a2+b2-c2;比较Δs1和Δs2的大小,选择其中较小的插入算法。

图4 算法及效果示意图
2.2.2 插入炮孔的顺序选择
选择先插入点示意图如图5。有p01,p02两个炮孔需要被插入到等时线上,那么如何确定哪个炮孔先插入进去呢?做法是先按照步骤1对p01,p02分别选出最优的插入位置,然后选出完成插入操作后路径最短的炮孔,则这个炮孔就被选择优先插入。
2.2.3 优化——去交叉
在完成上述操作后,基本上可以生成满足要求的等时线。经测试,上述方法在中等规模数量(150个炮孔左右)下没有问题,但是在炮孔数量庞大(200个以上)的情况下,偶尔会出现一两处交叉情况,如图6(a)。经过反复试验发现,出现交叉情况只会在少数情况而且在很小区域里,采用贪心算法矫正这部分的交叉即可(如图6(b))。

图5 选择先插入点示意图

图6 交叉情况示意图
矫正交叉过程如图7。p1-p4与p2-p5出现交叉情况如图7(a),只要将p1连到p2,p4连到p5即可消除交叉,如图7(b)。
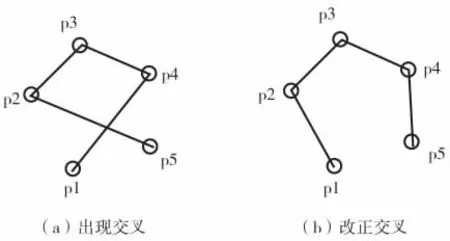
图7 矫正交叉过程图
3 测试结果
本程序的运行测试是在Windows7 32位操作系统上进行的,处理器是Intel CORE2 2.20 GHz,安装内存为2.00 GB。
对本文的算法进行了两方面的检测,首先用自动生成的大量炮孔进行检测,然后用实际爆破工程图进行检测。在采用自动生成的炮孔检测时,采用200个炮孔进行10次检测,发现生成的等时线符合要求,生成速度较快。在采用实际工程案例测试时,采用了10个规范布局图进行检测,发现生成的等时线满足工程要求。同时实际项目中等时线所花时间比均匀随机布孔花的时间少得多,主要是因为实际项目有多条等时线,每条等时线上的炮孔的数量较少造成的。具体测试数据见表1和表2。
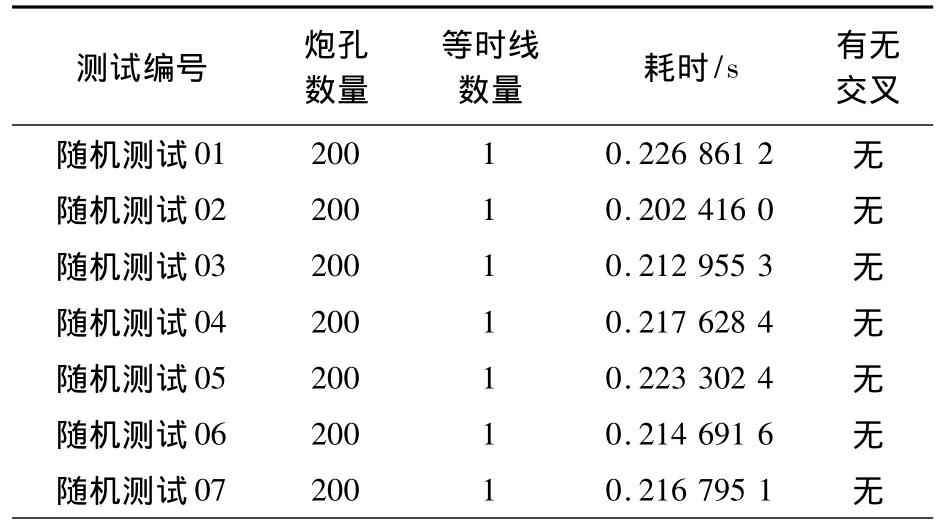
表1 均匀随机分布炮孔测试结果

续表

表2 实际工程案例测试结果
4 结语
本文主要探讨了基于凸多边形插入的爆破网络等时线的生成及优化算法,通过分层插入的方法使复杂的爆破网络具有清晰的层次,并且有条理地将每一个炮孔插入到相应的等时线上,最后说明了插入过程中的问题及解决方案。通过具体的实验证明,该算法可以适用于复杂网络情况的等时线生成,并且可以达到较好的效果。
[1]张乐,颜景龙.起爆延期等时线的生成及其应用研究[J].工程爆破,2010,16(2):86-90.
[2]CHI Baoming,LI Zhijun,YE Yong.Study on the arithmetic of automatically drawing isoclines of groundwater level based on GIS[J].Journal of Jilin University(Earth Science Edition),2007,37(2):261-265.
[3]ZHANG Weiqin,QING Yan ,JIAN Xingxiang.Natural neighbor interpolation and its application to 2D grid of irregular data[J].Computing Techniques for Geophysical and Geochemical Exploration,2011,6(3):291-295.
[4]RONALD L G.An efficient algorithm for determining the convex hull of a finite planer set[J].Information Processing Letters,1972,1(1):132-133.

