铁道车辆不同等效锥度计算方法对比及软件编制
陈迪来, 曾 毅, 夏张辉, 杨 超, 贺梓豪
(1.上海应用技术大学 轨道交通学院, 上海 201418;2.中国铁路广州局集团有限公司 工务部, 广州 510088;3.中国铁道科学研究院集团有限公司 机车车辆研究所, 北京 100081;4.中国铁路广州局集团有限公司 广州动车段, 广州 510000)
等效锥度是评价轮轨接触状态的重要指标,直接关系到车辆运行的安全性和旅客乘坐的舒适性[1-3]。等效锥度过小时,铁道车辆车体容易出现低频晃动,发生“一次蛇行”;当等效锥度过大并出现“负斜率”特性时,铁道车辆容易出现转向架失稳报警和车体抖动,发生“二次蛇行”[4-5]。随着我国铁路里程日益增多,车轮和钢轨间的接触状态更加复杂,不同车辆与不同线路上的钢轨匹配后,等效锥度会发生明显变化。需要对等效锥度进行管理,确保等效锥度处于正常范围,保障列车运行的品质。
20 世纪60 年代,欧美各国开始研究蛇行运动和轮轨接触对车辆运行平稳的影响。经过多年研究,确定了等效锥度的计算原理以及应用标准。国际铁路联盟和欧盟铁路技术规范对服役车辆的等效锥度限值给出了不同的建议限值[6]。标准EN 15302 用于等效锥度算法的验证,标准UIC 519 给出了等效锥度的计算方法[7]。国内铁道车辆领域内很多研究工作探讨了等效锥度和车辆动力学性能的关系,比较等效锥度计算方法间的不同之处。通过镟修车轮、打磨钢轨、焊接接头不平顺区间等检修方法,可以明显改善车辆运行过程的稳定性[8]。轮轨参数的变化也会导致轮轨接触几何关系发生改变,影响高速列车动力学性能。等效锥度广泛用于表征轮轨接触几何,却没有考虑非线性接触,简单描述更好的方案以解释接触非线性对铁路车辆运行动力学的重要影响[9]。虽然等效锥度与轮轨接触状态间没有出台具体标准,但是依据等效锥度对车轮廓形及钢轨廓形进行动态检测及管理,进而决定车轮廓形的镟修及钢轨廓形的打磨是非常有效的[10]。既有计算等效锥度软件大多数都是使用商业软件(如SIMPACK、ADMAS 等)中某1 种计算公式,并且1 次只能计算某一个车轮廓形和一个钢轨廓形间的等效锥度。随着智能运维系统中测量的轮轨数据越来越多,单一计算方法及单次计算不能很好表征出不同轮轨间的特征。因此,有必要研究出批量计算等效锥度的计算程序及不同计算方法对比的软件,方便铁路工程师对大数据时代下的轮轨数据进行批量管理和提取有效信息。
本文首先介绍了不同等效锥度的计算方法及影响因素,研究了不同计算方法间的差异,编制了批量计算等效锥度的软件,并对标准及磨耗后LM车轮踏面与r60 钢轨间等效锥度进行了计算,同时建议以轮对横移量为2 mm 处等效锥度作为3 mm 等效锥度的补充,用以评价轮轨接触状态,为智能运维平台中等效锥度的管理提供参考。
1 等效锥度的计算方法
等效锥度通常是根据车轮踏面的滚动圆半径差(rolling radius difference,RRD)函数(见式(1))求得。RRD 函数就是轨道车辆左、右车轮的滚动半径差随轮对横移量变化的函数[10]。下面对UIC 915 积分法、简化法、简谐线性法、线性回归法、概率法进行简单介绍。
1.1 UIC 519 积分法
轨道车辆运行过程中,自由轮对在轨道上的运动可以用下式来表达:
车辆运行速度为常量v=dx/dt,其中x为纵向位移量;t为运行时长;由此即可得:
根据速度v得到的关系式联立,综上得:
将被测车轮踏面锥度角假设为γ,可以得出车轮滚动圆半径差Δr与γ相关的关系:
用含有γ的式子表示出Δr并代入式(4)中:
x=0 时,y=0 且dy/dx=0。继续将转化后所得到的常数系数的二阶微分方程求解,得到结果即为Klingel 公式(见式(7))的正弦波波长λ,即:
Klingel 理论中指出的锥形踏面轮对在线路上具有相对固定的正弦运动轨迹,这一运动轨迹的波长取决于轮对踏面的锥度以及左右轮轨接触斑之间的距离[7]。等效锥度为波长相同的锥形踏面锥度角的正切值,即为Klingle 理论中的tanγ。线性化方法对轮对的周期运动做出假设,引入参数λec作为等效锥度,积分得到车轮运动波长,将其与Klingel 公式中的正弦波波长λ比对,相同波长下的锥形踏面的等效锥度数值作为结果,经转化得出式(8):
1.2 简化法
简化法将轨道车辆的等效锥度近似的以理想状态下锥形车轮踏面来表示,把理论上的锥形踏面滚动圆附近的一段为常数的直线段设为斜度λ。计算时通过滚动圆半径差Δr和轮对横移量y,建立关于近似等效锥度λ的值,当轮对横移量发生改变时,λ也会改变,将此时数值作为等效锥度λec(见式(9))。
1.3 简谐线性法
车辆运行时将车轮的横向移动看作是简谐运动,假设由转向架轮对系统性质决定的周期运动,相当于轮对所受的力与轮对的位移呈正比关系,将轮对横移量y假设为正弦运动。建立一个关于轮径差的“描述函数”,描述函数法是从频率域的角度研究非线性控制系统的稳定性的一种等效线性化方法。为使离散的非线性方程f(y)线性化,并使之与近似的线性方程f(y)≈kx的二次误差最小化[11]。因此,有式(10):
对上述关系式求导可以得出k的函数表达式:
进行求解得出x=Asinθ,其中A为谐波线性化幅值。
通过描述函数的线性化处理,近似的可以得出与线性化幅值A有关的等效锥度的表达式(见式(12))。轨道车辆的等效锥度与轮对横移量有关,当A改变时,得到等效锥度λec。
1.4 线性回归法
线性回归是一种以线性模型假设来拟合自变量与因变量之间关系的方法。通过将RRD 函数的拟合曲线分段,并对其每个区段进行一阶线性回归计算,可以得到自变量为轮对横移量y;一次项系数为k的一次函数,再对每一区段拟合后所显示的直线函数斜率的1/2 近似地作为等效锥度。线性回归算法的拟合方程式(13)如下所示:
由该函数方程式可以看出,斜率为k,则被测车轮的等效锥度λec即为式(14):
1.5 概率法
概率法认为列车在无蛇行失稳的情况下,轨道车辆运动过程中轮对所发生的横向运动属于一种服从正态分布的随机运动。与线性回归法相同,采用概率法计算时首先要对RRD 函数进行直线拟合。假设得到的拟合函数与RRD 函数间存在一定误差,将该误差设为E的函数关系式(见式(15)):
正态概率密度函数为:
当RRD 函数服从正态的概率分布,使E具有最小的拟合直线常数,可以得出函数斜率k和常数量b的表达式(17):
为计算出函数斜率k具体取得的数值,对式(17)中各项用积分表示,得到如下表达式组(18):
实验表明在多数运行情况下,振幅±4 mm 范围内,概率密度函数中常数σ=2.5 mm,新轮对µ=0,正态分布函数常数a需要满足如下式(19):
计算出表达式组(18)中各项参数的值,代入得出k的 1/2 为等效锥度λec(20):
2 等效锥度算法的编程实现
轮轨接触应力是影响轮轨磨耗和接触疲劳的重要因素,在相同的法向轮轨力作用下,轮轨接触面积越大接触应力越小[12]。轮轨接触点和滚动圆半径差也是2 个重要参数,计算接触点面积能够初步推算出等效锥度的情况和运行的状态,改变轮对横移量和修正轮对侧滚角可以计算左右两侧轮轨的最小垂向距离,比对后输出轮轨接触点计算值。滚动圆半径是车轮在运动状态下,用于计算车轮周长等于车轮实际运行的距离的等价半径,两侧滚动圆半径之差为Δr,结合RRD 函数对等效锥度进行求解。等效锥度要确定轮对横移量和滚动圆半径差的关系,通过不同算法的使用,其应用的计算场合和精度也有所不同。
2.1 UIC 915 积分法
使用插值函数找到左右轮滚动圆半径差为零时所对应的点,分别对左右不同轮对的横向位移范围进行相关约束,继续使用插值函数得出左右车轮的RRD 函数曲线。根据引入的边界条件采用三次样条插值对函数进行曲线拟合和不定积分输出其各自区间内的函数图像。
对左右轮轨等效锥度取值,计算并输出摇头角与等效锥度的图线。对轮对摇头角使用3 次样条插值完成曲线拟合,将拟合后的函数曲线进行不定积分整合,取规定范围内不同的锥度值在函数中评估数值经过计算得出波长λ。可以根据已知的Klingel 公式转化求得所需的等效锥度数值。
2.2 简化法
简化法是等效锥度的计算方法中较为简单的一种算法,利用滚动圆半径差和轮对横移量的插值函数关系表示出轮轨间的锥度。改变横移量数值,车轮锥度的大小会发生变化,以此时所采用的数据点计算出来的锥度即可认为是轮轨等效锥度。简化法在编程过程中数据的取值范围比较小,因此存在一定的局限性,可以推测出输出数据的图像误差会比较大,但其名字简化法的含义就在于计算和编程过程比较简单也是一种特殊的算法优势。
2.3 简谐线性法
简谐线性法编程时需要将测量等效锥度的轮轨的横向运动假设为简谐运动,设置调和函数参数θ在0 到2π的区间,间隔π/100 进行取值。描述函数是对非线性特征在正弦信号作用下输出进行谐波线性化处理所得到的近似描述[13]。需要先得到一个关于轮径差Δr的“描述函数”,然后对计算得出的进行曲线拟合,再将谐波准线性曲线进行不定积分,并分别按照其基本区间绘制出图像。调用fnval 函数在区间内2π点对函数描述评估,再经过计算得出等效锥度数值。
2.4 线性回归法
线性回归法是在存在2 种及以上变量的情况时可以使用的一种统计分析定量关系的方法,通过数理统计中的回归分析可以确定变量之间的定量关系。
在编程时同样先规定等效锥度的取值,通过polyfit 函数进行阶数为一的最小二乘法直线拟合,得到的P1(1)数值即为函数表达式的一次项系数,即函数斜率。已知等效锥度等于斜率的1/2,简单计算后即可得出结果。
2.5 概率法
概率法编程设置等效锥度的范围取值并对RRD 函数进行插值处理,下一步引入正态分布概率函数σ。根据正态分布函数的性质可以得知,函数曲线在横坐标为µ时两侧曲线对称。当µ值固定时,随着σ数值的增大曲线越趋于陡峭,且当输入车轮踏面为新踏面时,默认µ值取0 计算概率函数的常数。根据正态概率分布式(16),以MATLAB程序语言的形式表达,计算出给定截面上的概率函数。
对于拟合的函数直线,同样根据上一章节内容已知关于其斜率k值的函数,分别对关系式中的各个组成部分进行积分,再将其代回式中计算出k值取1/2 作为等效锥度的数值。
3 计算程序
3.1 程序介绍
通过MATLAB 软件对计算程序的操作界面和算法编程,设计了2 个独立操作的GUI 控制操作界面,分别命名为“轮轨几何接触计算程序”(见图1)和“等效锥度计算程序”(见图2)。轮轨接触和等效锥度结果分开,使输出的各部分图像清晰明了便于辨识,同时数据有机地结合,实现从数据输入、参数设置、结果计算和图像输出等环节。点击图1 中“Left Wheel”“Right Wheel”可以单一或者批量导入车轮廓形,点击“Left Rail”“Right Rail”可以单一或者批量导入钢轨廓形,实现轮轨接触几何的批量计算,能为铁路工程管理轮轨外形节约时间。

图1 轮轨接触几何计算的操作界面Fig.1 Operating interface for geometric calculation of wheel-rail contact
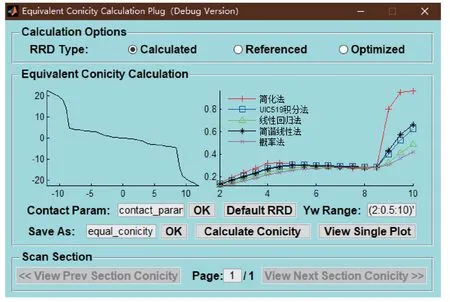
图2 等效锥度计算的操作界面Fig.2 Operating interface for the equivalent conicity calculation
主控制界面主要由设置、加载文件、插值、装配等部分组成。加载文件后按需求更改4 条曲线方向,确保数据处于合适的计算状态。确认插值和匹配,进行下一步计算可以分别得到左右两侧的轮轨接触点、轮径差、滚动角等数据曲线,底部设置的切换按钮可以在批量输入轮轨数据时浏览各组图像。
等效锥度计算模块可以实现对任意车轮计算等效锥度。将等效锥度算法独立编程完成后分别保存,并连接嵌入到计算程序中。在下方的等效锥度计算区域中,通过对接触参数设置后可以直接调用轮轨接触计算模块计算得到的RRD 函数以及计算得到的等效锥度曲线图像,操作程序底部的切换按钮可以实现当前与前后被测轮轨数据的显示切换,方便在多个数据输入程序时的批量计算和观察比较。
3.2 程序测试
载入“轮轨接触几何计算程序”和“等效锥度计算程序”控制程序。在设置选项部分设置长度单位为毫米(mm)、角度单位为弧度制(rad)以及计算模式。分别点击左右车轮踏面和钢轨廓形,通过预设路径将数据导入到程序中(测试采用LM 型踏面和r60 型钢轨),可以单击图像下方的“View”对输入的轮轨曲线(见图3)进行查看。选择“Multiple”模式,导入多个数据并通过“View”两侧的“Prev”“Next”进行上、下不同导入数据的切换。
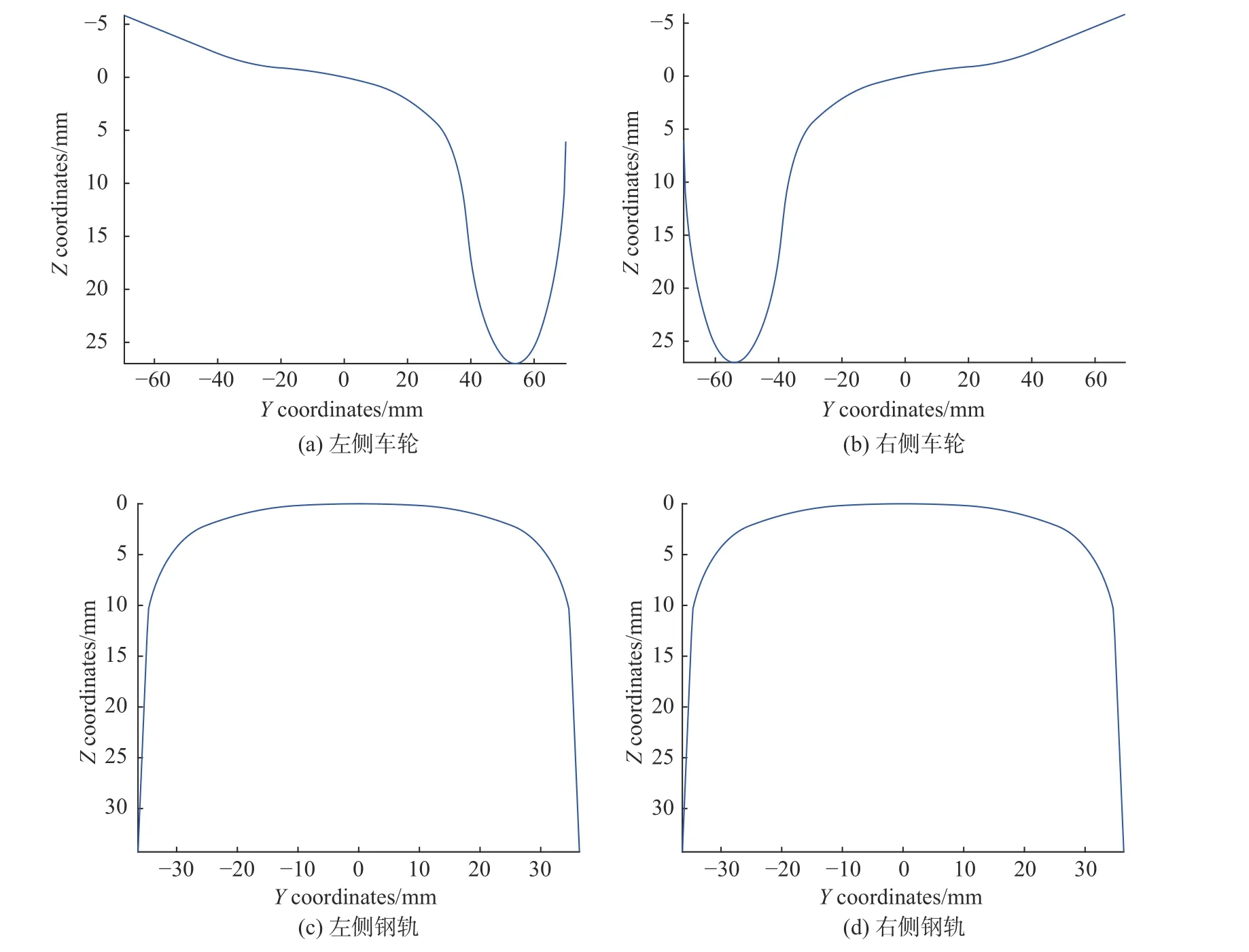
图3 轮轨曲线Fig.3 Wheel/rail profile
插值方法按需求设置,本程序提供了“linear”线性插值、“cubic”立方插值、“spline”3 次样条插值这3 种方法,可依照实际情况选择使用,调至合适的阶数点击“Apply”。输入轨道车辆的装配数据,本次采用标称半径420 mm、标准轨距1 435 mm、跨度1 493 mm 等,点击“View Assembly”对输入轮轨数据的匹配情况进行观察(见图4),对4 个不同方向的平面3D 配合图像检查完毕后,点击“Complete Assembly”确认。
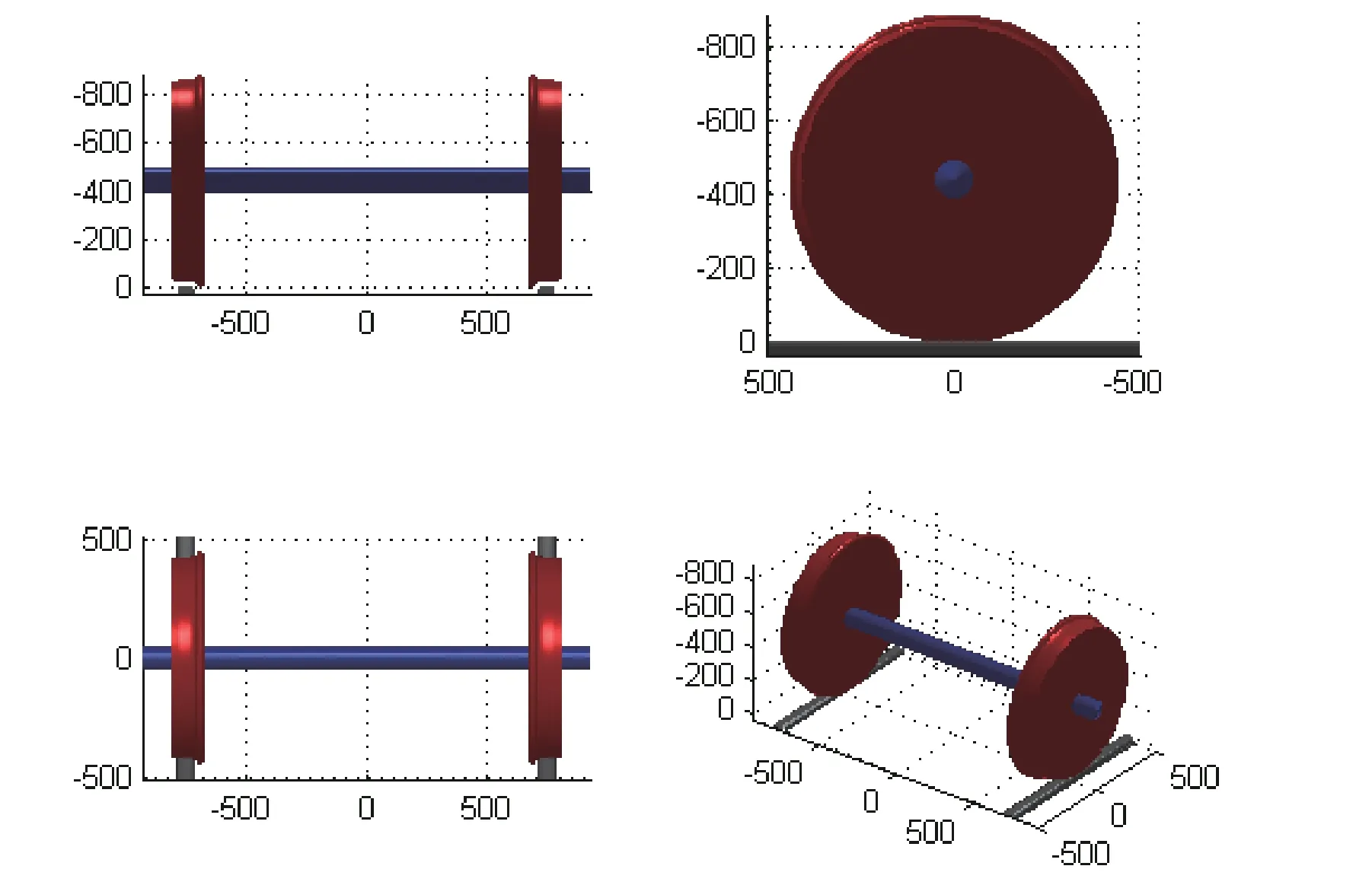
图4 装配图像Fig.4 Assembly image
按照测试需求进行设置以及装配参数调整完毕后,点击右上方的“Start Calculation”计算输入的轮轨数据和预设的装配数据,计算出部分几何参数图像(见图5),各个图像也同样支持单独放大查看。通过观察关于接触点、滚动角、轮径差等参数的曲线可以对当前轮轨的接触参数进行分析,发现配对维修的错误原因所在,及时解决问题提高检测效率。

图5 轮轨接触点分布Fig.5 Distribution of wheel-rail contact points
转换到等效锥度计算程序界面,将RRD 函数的类型选择切换到“计算”模式,点击“Default RRD”和“Calculate Conicity”将会在左右两个图表中分别显示出预设RRD 曲线(见图6)和采用5 种等效锥度计算方法得到的曲线(见图7)。

图6 RRD 函数曲线Fig.6 RRD function curve
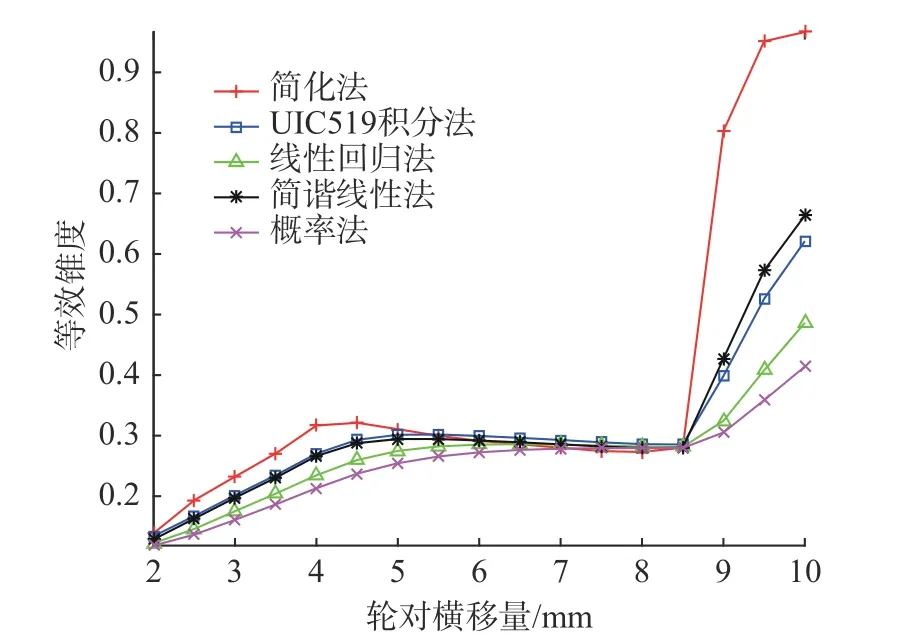
图7 等效锥度曲线Fig.7 Equivalent conicity curve
结合图6 和图7 可以看出,RRD 函数在轮对横移量为[–8.5, 8.5] mm 范围内,呈现线性趋势,此时各种算法计算得到的等效锥度基本相同。当RRD 函数有明显跳跃时,各种算法得到的等效锥度有较大的区别。简谐线性法和UIC 519 积分法的曲线在整个变化过程中,走向变化都基本吻合,在所有曲线开始突变时,二者间差异也最小。而采用简化法测得的等效锥度数值上升变化剧烈,中期较为平稳的阶段,下降趋势也十分明显。
选用1 组磨耗后的轮轨数据(LM 车轮踏面和磨耗60 kg/m 钢轨)进行测试。可以清楚的看到轮轨廓形在运行磨耗下发生改变,重复上文的测试步骤可以计算出磨耗后的部分轮轨参数(见图8)。

图8 磨耗后轮轨接触点分布Fig.8 Distribution of wheel-rail contact points after abrasion
操作等效锥度计算程序得到磨耗后的RRD 函数(见图9)和等效锥度曲线(见图10)。

图9 磨耗后RRD 函数曲线Fig.9 RRD function curve after abrasion

图10 磨耗后等效锥度Fig.10 Equivalent conicity after abrasion
结合分析图9 与图10,磨耗后的轮轨匹配后其锥度差距增大,RRD 函数非线性特征增强,使得各算法得到的等效锥度曲线差异较大。可以明显看出简化法与其他4 条曲线走势相差甚远,主要原因是简化计算直接将轮轨型面等效为线性变化的直线区段,当轮轨外形出现磨耗后,型面不再是单一直线,因此不建议对磨耗后的轮轨采用简化法计算等效锥度。由于等效锥度直接体现的就是自由轮对的蛇行运动,而简谐线性法和UIC 519 积分法都是将车辆运行轨迹近似看成正弦曲线,这种假设与实际轮轨运行最为接近,因此,采用简谐线性法和UIC 519 积分法计算数据较为准确。
选用1 组磨耗后的轮轨数据(LM 车轮踏面和打磨前60 kg/m 钢轨)继续测试,结果如图11 和图12 所示。
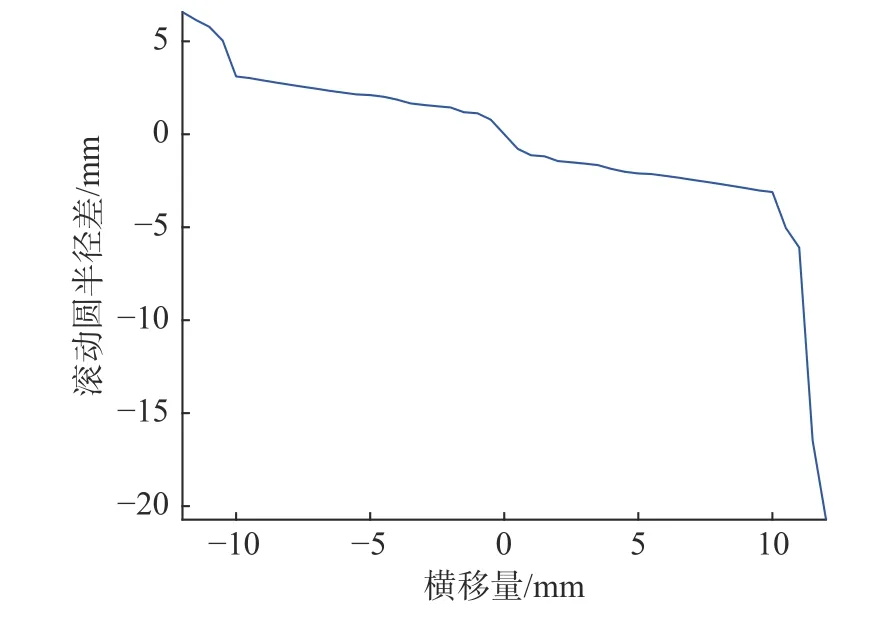
图11 打磨前RRD 函数曲线Fig.11 RRD function curve before grinding
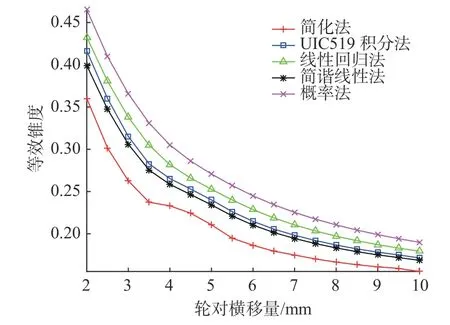
图12 打磨前等效锥度Fig.12 Equivalent conicity before grinding
国际铁路联盟UIC519 定义名义等效锥度指轮对横移量为3 mm 时等效锥度的计算数值,但若只采用单一某点(3 mm)处等效锥度来评价轮轨接触状态并预测车辆稳定性不是很全面。结合图11 和12 分析,等效锥度出现了“负斜率”增长,若只采用3 mm 时的数值往往较小,因此,建议增加轮对横移量为2 mm 时数值作为辅助评价轮轨接触状态。也可以看出,简化计算方法得到的等效锥度值与其余几种方法相差较大,不建议采用简化计算方法来评价等效锥度。
4 结 语
等效锥度直接反映了轮对蛇行运动的波长,通常采用RRD 函数求得。当RRD 函数呈现线性时,不同等效锥度的计算方法基本一致;当RRD 函数有明显跳跃时,不同算法计算得到的等效锥度值存在较大差别,尤其是在磨耗后的接轨接触中,简化法计算得到等效锥度差异较大,其余方法计算得到的等效锥度最为接近,能较真实地反映轮对蛇行运动的波长。同时建议采用轮对横移量为2 mm 处的等效锥度作为3 mm 等效锥度的补偿,以免局部某一点的较大误差影响了等效锥度的计算结果。等效锥度用以评价轮轨接触状态,能及时对车辆的廓形进行镟修和指导钢轨打磨。

