基于卷积神经网络的Gray-Scott 模型图像分类算法
李艳秋, 朱鲁帅
(1.上海应用技术大学 理学院, 上海 201418;2.南京工业大学 数理科学学院, 南京 211816)
图灵发现不均匀的图案或空间非均匀性可能来自扩散,称为图灵不稳定性[1]。从生物学角度看,生物体呈现的斑图是由基因和体内的化学反应决定的,对斑图分类的研究有利于探索斑图形成的理论机制和生物学根源,甚至可以揭示某些疾病产生的原因和基因的异常表达,作为预防疾病的手段。图灵斑图是从理论上研究自然界存在的真实斑图,从计算机或人工智能角度来讲,计算机认识世界的基础就是对这些斑图进行分类,有了分类之后才可能进一步做更细致的视觉任务。那么,斑图的分类是非常有必要的。
斑图分类依赖于图像分类技术。图像分类领域的较快发展是由于深度学习的发展。在图像分类问题上,深度学习算法比传统的机器学习算法有更大的优势。特别是,卷积神经网络在图像分类问题上模仿了人类大脑中神经元识别斑图的方式,神经网络通过训练数据,然后通过迭代学习权重的最佳值,并在训练数据中提取重要的特征,从而确定规则。经过大量的研究表明,神经网络是图像分类的有效方法[2-4]。此外,聚类分析也是图像分类的重要方法,它是一类无监督的学习算法[5-7]。使用聚类算法可以提高图像分类的准确性和效率[8]。由于数据本身具有定性或定量的特征,可以通过聚类分析对大量的数据进行分类和分组以了解数据集的内在结构。
1 文献综述
图像分类是使用计算机将图像内容分成不同的目标区域并描述分类。由于计算机技术的飞速发展,图像分类作为计算机视觉的核心问题之一,是人工视觉判读的延续和发展,计算机图像分类比人工图像分类要快得多,分类精度也达到了很高的水平。在“信息爆炸”的今天,图像信息的获取和使用越来越方便,图像文件的交换和传输越来越频繁[9]。
随着图像分类领域研究的不断深入,很多学者提出了不同的图像分类算法。Kekatos[10]于1993年提出了支持向量机(support vector machine,SVM)算法,该算法可以通过核函数将输入空间中的非线性可分离数据映射到高维特征空间。然而,支持向量机算法不能很好地处理大量、多样的图像。K 近邻算法具有较高的精度和稳定性,但容错性较差,效率较低。传统的图像分类方法对于一些简单的图像分类是有效的,但它们被实际情况的复杂性所淹没。经过近几年人工智能领域的快速发展,深度学习已广泛应用于金融业、工业制造、智能驾驶等领域,并取得了显著的成果。卷积神经网络(convolutional neural network,CNN)作为深度学习的代表算法,可以有效地处理高维数据。LeNet5 是Lecun 等[11]于1998 年为手写数字设计的卷积神经网络,出现在2010 年开始的ImageNet挑战赛中,在目标检测和识别方面取得了良好的结果。此后,学者们优化了CNN 结构的输入和特征提取,提高了模型的泛化性能。
本文对图像分类进行了深入研究,通过对斑图的分类可以更好地了解环境因素的变化对生态系统的影响以及形成生态现象的机制[12-24]。然后,利用机器学习中的特征工程方法获得更好的图像训练特征。使用人工神经网络和聚类算法对系统生成的点、线状图数据进行了更详细的讨论和分析。众所周知,深度学习框架只能被视为提供非线性回归[15],但本文所讨论的特征工程与其相反,允许通过单层神经网络对具有非线性的数据特征进行有效分类和聚类。
2 图像分类算法的基本原理
由于受到哺乳动物视觉过程的启发,CNN 的工作原理更接近于生物意义上的神经网络,可以有效处理二维图像数据,是深度学习快速发展的重要推动力之一。CNN 最大的创新是采用了局部连接和权重共享的思想,改进了层与层之间的连接形式,用局部连接代替了多层感知器(multilayer perceptron,MLP)的全连接,因此,CNN 可以看作是MLP 的一个变种。
目前,卷积神经网络被广泛应用于目标检测、图像分割和自然语言处理等领域,由于其强大的特征表示能力,越来越多的学者开始探索和研究它的学习能力。基本的网络运行过程主要是通过从大规模样本中学习相关特征,并在测试过程中能够评估性质相似的测试数据。因此,卷积神经网络有3种主要网络结构:卷积层、池化层和全连接层。
卷积层主要对输入数据进行特征提取,并对输入数据中的隐含关联性进行采样,类似于图像过滤操作。卷积过程通常可以看成是权重矩阵与图像矩阵的乘法。在操作过程中,图像上的每一层像素矩阵被卷积核以指定的像素距离扫描,扫描的图像区域所对应的数值被相乘,然后相加,得到卷积操作后尺寸较小且失去边缘信息的特征图。卷积后的输出图像大小为:
式中:Oh和Ow分别表示卷积操作后特征图的高度和宽度;M为卷积操作前的输入图像;Mh和Mw分别为输入图像的高度和宽度;Kh和Kw分别为卷积核的高度和宽度;P为卷积操作时输入图像边缘的像素点填充;S为卷积核每次移动的像素距离,也叫步长。
卷积的计算过程有2 个主要步骤:①矩阵内积乘法;②内积乘法结果的求和。2 个元素在同一位置的矩阵的乘法,得到1 个新的矩阵。这个新矩阵的所有数值求和,得到1 个数值,就是卷积运算的结果。
池化层是基于局部相关的思想,通过对1 组局部相关的元素进行抽样或信息聚合,得到新的元素值,本质上属于降维采样的过程。其主要目的是为了神经网络在训练和学习过程中去除冗余信息、压缩特征、简化网络的复杂性,一般理解为减少参数数量,在一定程度上可以避免过拟合的发生。
全连接层(fully connected layer,FC)在整个卷积神经网络中充当“分类器”。当卷积层和集合层将原始数据映射到隐藏的特征空间,全连接层则起到将学到的“分布式特征表示”映射到样本标记空间的作用。
在卷积神经网络中,卷积和池化这2 个线性网络层构成了整个模型,所以模型的多层网络级联仍然是线性的,这种线性关系只能处理线性可分的问题,但通常遇到的问题是非线性的,所以需要使用激活函数来增强网络的非线性表达。常见的非线性激活函数有Sigmoid、ReLU 和Tanh。Sigmoid是1 个常用的非线性激活函数,其数学表达式为
式(3)能够不断地将输入的实值转化为0~1的输出。若为非常大的负数,输出就是0;若为非常大的正数,输出就是1。然而,梯度消失问题往往发生在反向传播过程中,模型不能正常收敛。
Tanh 部分解决了Sigmoid 关于零中心化(Zero-Centered)的输出问题。导数范围在(0,1)之间变得更大,而Sigmoid 在(0,0.25)之间,梯度消失的问题得到了缓解。Tanh 函数的数学表达式为
ReLU 函数使一部分神经元的输出为零,这就造成了网络的稀疏性,减少了参数的相互依赖性,缓解了过拟合问题。ReLU 函数的数学表达式为
3 斑图的产生机制
探索斑图的存在需要讨论稳态问题[16-17]。在这项工作的研究中,选择了Gray-Scott 模型来描述浮游生态系统[18]中斑图的形成:
式中:u、v分别代表t时刻浮游动物和浮游植物的种群密度;du和dv分别为2 种群的扩散系数;k和f分别代表由毒素释放造成的浮游动物死亡率和浮游动物有额外的食物维持种群的增长率[19-20]。Ω∈R2为有限区域,文中模拟时设定尺寸为10×10,模型具有周期性边界条件。
求解方程组
当然,对于种群模型[23-24],正平衡点处的动力学行为更值得关注。当T0<0,D0>0时,系统式(6)对应常微分方程的平衡点局部渐近稳定,若加入扩散项之后,式(6)的平衡点变为不稳定状态,此时会出现图灵斑图。
图1 显示了在du=1 和dv= 0.5 时,基于系统参数k和f的相位图。图1 中的灰色区域代表正平衡点稳定状态。在不稳定区域,Gray-Scott 反应扩散模型产生各种形状的图案,包括“条纹状”“斑点状”“倒斑点状”和混合形状图案。不同字母代表不同模式斑图。
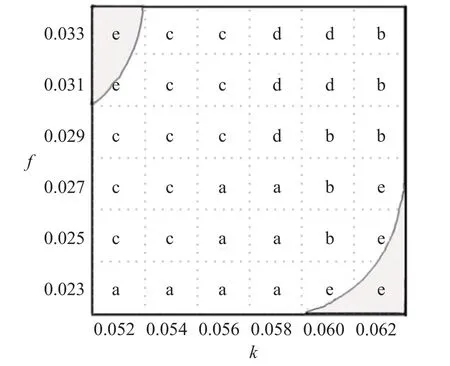
图1 du=1 和 dv=0.5 时,相位图随系统参数 k和 f的变化Fig.1 When du =1 and dv =5, the phase diagram changes with the system parameters k andf
图2 显示了在固定扩散系数du=1 和dv= 0.5 的情况下,通过改变参数k和f产生的图案。定义了5 000个模拟秒,其中每个模拟秒4 步。

图2 系统(6)斑图随k-f的变化Fig.2 Describe the changes in the system’s (6) pattern with respect tok-f
4 斑图分类过程
选择了4 组不同模式的斑图,见图3。对应参数:(a)f=0.021,k=0.052;(b)f=0.023,k=0.060;(c)f=0.027,k=0.056;(d)f=0.029,k=0.060。利用神经网络框架对这4 组斑图进行分类。所有生成的4 组斑图的训练集和测试集按7∶3 的比例进行训练,并将其送入位于64×64 的像素矩阵中。
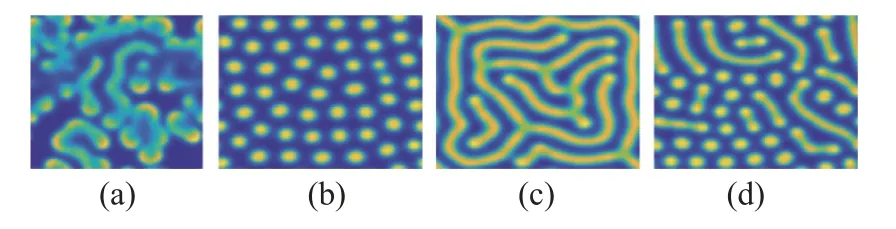
图3 Gray-Scott 反应扩散模型生成的4 种斑图Fig.3 Four plaque plots generated by the Gray-Scott reaction diffusion model
使用单层神经网络对图像进行分类,为了将神经网络应用于4 类别分类,使用包含4 个输出节点的输出层对神经网络进行训练。上述结构的所有训练过程如下:
(1) 随机初始化网络中的所有权重。
(2) 使用梯度下降(gradient descent,GD)和Adam 优化器对672 幅图像进行了2 000 次迭代训练。
(3) 使用288 张图像验证分类的准确性。
在训练前确定适当的样本特征可以提高分类的准确性,利用斑图的特征而不增加神经网络的层数来提高分类准确率。
利用先验知识将神经网络转化为一种特殊形式。由于输入图像是非线性的,传统的层次结构Z=WX+b(其中X表示特征,W、b分别表示训练权重和偏置项)计算精度不高,因此,在本文中,将传统层结构的模型定义为基线模型。由于区域、层界面位置和分布可以用于区分球形、条纹和斑点以及混合斑图。所以,修改后的模型与基线模型进行比较,使用非线性函数、梯度、拉普拉斯等修改后的特征能够更好地反映。考虑以下Ginzburg-Landau 自由能的泛化[25],
式中,d1、d2为系数。式(9)可以通过模拟相位分离产生复杂的图案,而形成的图案是由条纹状和斑点状图案组成。如果式(9)可以生成各种复杂图案,那么生成的图案就可以按照这样的方法进行分类。在文献[14]中,给出了2 种不同的图像数据下X,(1-X2)2和∇X的网格图。提出对于给定的图像数据,∇X和(1-X2)2可以呈现条形或圆形的体积和界面区域。
通过式(9)的变分求导来推导出以下广义函数的最小点:
式中:Y是非零固定变量;〈,〉是内积。基于上述结论,神经网络前向传播如下:
式中:σ表示激活函数;b表示误差项;∇X和X-X3为特征;对应的权重分别为W1和W2,如果在同一个单层神经网络中有2 个特征,则应该使用2 个权重,以防止数据集拟合不充分。
在本文中,使用具有2 个输入特征的单层神经网络分类器,对2 个输入特征分别进行加权,与1个偏置项相加,通过激活函数获得输出,然后使用反向传播算法训练神经网络。反向传播算法是一种迭代算法,在该算法中,对于每个输入特征,在单个网络层中分别训练2 个权重,每个权重通过独立的反向传播进行更新,以使目标的误差更小。最后,重复前面的步骤,直到停止训练。图4 是1 个具有上述2 个输入特征的单层神经网络的结构示意图。

图4 2 个输入特征的前向传播神经网络结构Fig.4 Forward propagation neural network structure for two input features
表1 展示了通过上述分析得到的在GD 和Adam 优化器下,单特征和双特征神经网络的训练精度。由表1 可见,本文提出的模型与基线和其他模型,在GD 和Adam 优化器下都取得了明显的改进。此外,不同的特征对神经网络的收敛速度也有很大影响。与其他模型相比,双特征模型可以用较少的迭代次数(600 次)收敛分类,而单特征模型则需要2 000 次的迭代才能收敛。

表1 单特征和双特征GD 和Adam 优化器测试精度对比Tab.1 Comparison of test accuracy among single-feature, dualfeature GD and Adam optimizer
5 实例分析结果
聚类就是把1 个给定的数据集按照某个特定的标准进行分割,通过将其分割成不同的类或者簇,使得同一类的数据对象的相似性尽可能大,同时不在同一类的数据对象之间的差异性也要尽可能大[26-27]。为了更加深入地去了解聚类算法,使用上面讨论过的特征和图2 中的所有斑图来对数据进行聚类。对于聚类的好坏,可以通过聚类结果进行验证。簇间距离越大,聚类效果越好;簇内距离越小,聚类效果越理想。
图5 表示的是二维空间中36 种斑图的可视化。相同颜色的点代表相同类型的斑图。通过使用每个特征的均值和方差,在二维空间中以每个斑图20 个点来可视化所有斑图。其中,图5(a)是使用∇X和X-X3的平均值进行聚类。从图中很容易看出它是8 个聚类,这将是一个好的聚类。当然,聚类的数量最初是未知的,主要是由于斑图的复杂程度决定。图5(b)是使用∇X和X-X3的方差的聚类结果,与图5(a)相比,使用方差的聚类效果远不如使用均值的聚类。图5(c)是使用∇X的均值和X-X3的方差进行聚类的结果。图5(d)是使用X的均值和X-X3的方差进行聚类的结果。通过对上述4 种聚类结果可以看出,图5(c)和(d)的聚类结果差别很大,聚类标准比较模糊。

图5 二维空间中36 种图案的可视化Fig.5 Visualization of 36 patterns in two-dimensional space
为了更加直观的看出聚类的效果,使用图5(c)、(d)中X、∇X的平均值和X-X3的方差这3 个特征在三维空间中对所有图案可视化,其中,每个图案代表40 个点。结果如图6(a)所示。通过肉眼可以看出,聚类效果比以前要好。

图6 将总共36 个图案且每个图案40 个点在三维空间(a)中进行可视化,可视化三维空间(b)中的每个图案上的点都代表相同颜色的相同簇中的点Fig.6 Visualization of a total of 36 patterns with 40 points per pattern in 3D space (a), where the points on each pattern in 3D space(b) represent points in the same cluster of the same color
最后,使用120 个数据点的平均值在三维空间中进行聚类分析,将集群的数量设置为5,用相同的字母来代表每个聚类的斑图。
根据之前的聚类,通过图7 来表示每个聚类的斑图。其中,图7(a)~(d)是图3 选择的斑图,图7(d)是复杂斑图,图7(e)表示稳定状态。实线以内的区域满足稳定性条件。它与图2 有很好的一致性。
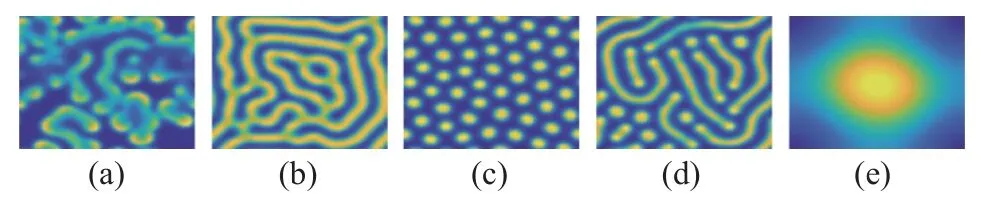
图7 用字母表示每个簇的图案Fig.7 The representation of the pattern of each cluster with different letters
6 结 语
本文以毒素作用下浮游动物和植物生态反应扩散模型为媒介,分析了系统共存平衡的图灵不稳定性是产生斑图的先决条件。然后利用机器学习方法中的特征工程对图像进行分类。通过可视化结果可以看出,特征∇X和X-X3比单一特征具有更好的分类和聚类效果。考虑到所用斑图的高度非线性,训练的高精度和低迭代速度仍需在未来改进,神经网络在反应扩散动力系统中的应用将一直是学者们关注的热点问题。同时,对所有高度相似的斑图进行更精确的分类和聚类是一个非常具有挑战性的问题。这将是非线性偏微分方程演变和图像分类技术的重要部分。

