三锚系大型浮标运动响应特性数值研究

高洋洋，胡阳宁，王立忠，李培良

（1.浙江大学 海洋学院，浙江 舟山 316021；2.浙江大学海南研究院，海南 三亚 572025）

随着海洋油气矿产、海上风电和渔业等资源开发力度逐渐增大，如何准确获取所在海域的海洋环境水文气象资料，是海洋资源开发面临的重要难题之一［1-2］。与传统的固定式海洋环境监测装备相比，海洋浮标因其具有在复杂海洋环境中可开展定点、长期、连续的风浪流等海洋环境数据实时监测等优势［3］，在海洋资源开发中得到广泛应用。

浮标结构运动响应和锚泊系统设计直接关系到浮标系统的稳定性和可靠性，影响浮标的施工布放与安全运维［4］。Carpenter等［5］和Jenkins等［6］分别针对圆盘和圆柱形式浮标开展了随机波浪作用下其运动响应特性的数值模拟和试验研究，研究表明圆盘浮标在涌浪情况下横摇响应幅值较大，圆柱浮标在涌浪情况下垂荡响应辐值较大［7］。李家来和谢宇新［8］对不同直径的圆盘形式浮标开展了水动力性能分析，结果表明，随着浮标直径的增大，RAO 的幅值逐渐降低，浮标随波性能变好。缪泉明等［9］基于三维势流理论研究了10 m 圆盘浮标的水动力和动态响应特性，对极限海况下不同水深的三锚系统浮标运动响应与锚链张力进行了数值模拟计算，为浮标标体与锚泊系统的设计提供参考。董春明［10］对浅水环境下潮流能装置的锚泊系统进行数值模拟研究，结果表明，含有浮筒的装置可在很大程度上减小系泊链张力，抵御强台风。李珂翔等［11］采用格林函数法分析了不同间距、位置分布对多浮体水动力特性的影响，研究发现浮体分布夹角对浮体水动力系数的影响随着间距的减小愈加显著，在浮体间距较大时，夹角对水动力系数的影响不显著，浮体间距与波浪的相位关系占主导因素。Li 和Wu［12］将Kotorayama 方法从单点系泊问题扩展到多点系泊问题，在时域内对多根锚链系泊的浮标水动力特性进行了研究，分析了浮标运动响应与波高的关系，结果表明，作用在系泊锚链上的水动力荷载会对浮标的运动响应产生显著影响。Paul等［13］和Tsukrov 等［14］研究发现悬链线式和张紧式系泊方式的浮标结构力学性能和运动响应存在较大差异，在特定海况条件下悬链线系泊方式产生的动态张力可达到张紧式的3 倍。Zhang 等［15］和张素侠等［16］研究发现，系泊缆在松弛—张紧过程中产生的瞬态荷载远大于正常工况下的动态张力，该瞬态荷载与系泊缆长度、刚度、材料特性相关。Hsu 等［17］对波浪作用下循环运动锚链张力特性研究发现，受冲击张力作用的影响，锚链最大张力比未发生冲击张力情况下增大约37%～68%。Gao 等［18］开展了往复激励下浮标锚链动力响应特性试验，研究了运动自由度、运动周期与幅值以及锚链初始形态对于锚链非线性张力变化的影响。结果表明锚链非线性动力响应主要受预张力与运动周期影响，在较小运动周期与较大预张力下，锚链运动响应与动态张力变化呈现较强的非线性，锚链顶部动态张力由多个谐波分量组成，较大预张力时锚链在水平和竖直激励作用下均会产生张力极值突变现象，不同运动自由度会显著影响锚链动态张力极值。

近年来随着海洋牧场的建设，连续定点立体海洋要素观测的需求增加，浮标可定点、长期、连续监测海洋水文气象数据，已成为最主要的海洋环境监测手段之一［3］。蝶形浮标和圆柱浮标随波浪运动剧烈，会对部分传感器电子元器件的使用产生影响［19］。大型浮标具有容量大、抗恶劣环境、抗破坏性强等特点，适合近海区域的长期定点观测［20］。为了克服恶劣环境诸如台风海况条件对浮标监测系统的影响，如何提高浮标的适用性、可靠性及安全性显得尤为重要。锚泊系统的设计关系到浮标的安全运维，在浅水环境下浮标锚泊系统的设计较深水环境而言更为复杂，需要满足锚链张力与定位的难度更大。在浅水锚泊系统设计时，需要延长躺底段长度以增加锚链的系泊力，占用的水域面积增大，相应的成本提高；若降低锚链预张力，增加躺底段锚链的相对长度，则导致浮体的运动幅度增加，加剧浮体的运动响应［21］。中国东南沿海台风频发，极易发生浮标走锚事故，且受海底观测设备电缆与锚泊系统缠绕问题等安全因素的限制，影响海洋环境要素的连续性观测［22-23］。因此亟需研发适用于近海海洋牧场可长期、稳定、连续、实时观测海洋环境要素的大型浮标［24］。

综上所述，以三锚系大型浮标系统为研究对象，开展了浮标系统水动力与动力响应特性数值模拟研究，分析了浅水环境下浮标附加质量、辐射阻尼、运动响应幅值算子RAO等水动力参数，阐明了不同风浪流工况下三锚系浮标系统与辅助浮筒的运动响应特性，揭示了浅水环境下三锚系浮标锚泊张力变化规律。研究成果可为三锚系浮标系统的设计优化提供理论依据和技术支撑。

1 数学模型

1.1 控制方程

基于势流理论开展了三锚系大型浮标系统水动力特性研究，假定流体为均匀、不可压、无黏性、无旋的理想流体［25］，将浮标周围波动场内任意一点的速度势记为ϕ(x，y，z，t)，关于速度势的求解可分为以下3 个部分：

其中，ϕI(x，y，z，t)为入射势，ϕD(x，y，z，t)为绕射势，ϕR(x，y，z，t)为辐射势，其中绕射势和辐射势合称为散射势ϕS。

基于三维势流原理，考虑静水回复力和波浪激励力的作用，频域内规则波作用下浮标运动平衡方程［4］为：

其中，M表示浮标质量矩阵，μ表示浮标附加质量矩阵，λ表示阻尼矩阵，C表示浮标静水回复力矩阵，即系统刚度矩阵；Ẍ、Ẋ、X为浮标6 个自由度运动的加速度、速度和位移，6 自由度分别为纵荡、横荡、垂荡、横摇、纵摇、艏摇；F为波激力。

时域内浮标系统运动响应方程［4］为：

其中，K(t-τ)为系统延迟函数矩阵；Fi(t)为作用在浮标的环境荷载；Fm(t)为锚泊系统张力。

基于计算流体力学水动力软件AQWA 与OrcaFlex 开展了三锚系大型浮标系统水动力特性数值研究。AQWA 软件是由ANSYS 开发的海洋工程结构水动力分析软件， 通过势流理论求解速度势拉普拉斯方程，可进行各种浮体的水动力性能和各自由度响应计算，获取浮体的静水刚度和RAO 值、附加质量和辐射阻尼等水动力系数。

OrcaFlex软件是由英国Orcina公司开发的动力学分析软件，搭载了三维非线性时域有限仿真程序，可以通过定义系泊缆段数和长度来实现有限元网格划分的效果，对浮体和线杆结构的耦合进行动力分析，对单点系泊、多点系泊等不同系泊系统进行静态和动态分析。

1.2 数值模型

三锚系大型浮标主要由10 m浮标标体、辅助浮筒和锚泊系统等部分组成，舱室主要包括电池舱、仪器舱及6 个浮力舱。桅顶平台可安装太阳能电池、锚灯、GPS 天线、避雷针及各种传感器等。辅助浮筒主要作用是避免锚泊系统与海底观测设备电缆发生缠绕，保证海底观测设备的正常运行。辅助浮筒上设有一体化航标灯与可视标志，增加浮标的可视度、安全性。

浮标标体结构示意如图1所示，浮标标体、辅助浮筒及锚泊系统主要设计参数如表1所示。该浮标直径为10 m，作业水深25 m，辅助浮筒直径为2.4 m，3 个辅助浮筒呈120°分布在浮标周围，辅助浮筒中心距离浮标中心24 m。浮标水动力计算模型与网格示意如图2 所示，锚泊系统坐标示意如图3 所示。浮标系统采用三点锚泊方式固定，海底锚固点距离浮标中心95 m，锚泊基础采用霍尔锚，浮标与锚泊基础、辅助浮筒之间通过锚链连接。

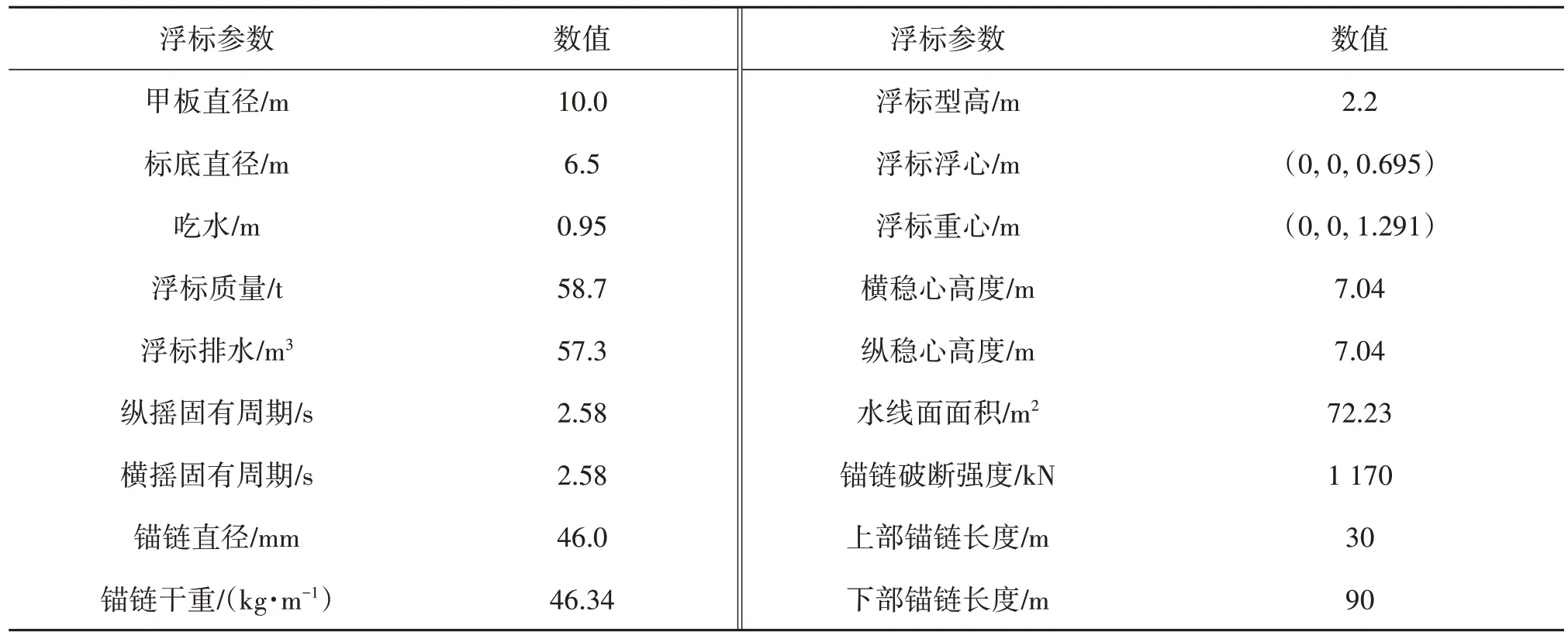
表1 三锚系浮标主要设计参数Tab.1 Design parameters of three⁃anchor buoy

图1 浮标标体结构示意Fig.1 Buoy overall structure

图2 浮标与辅助浮筒模型与网格示意Fig.2 Buoy model configuration and local mesh

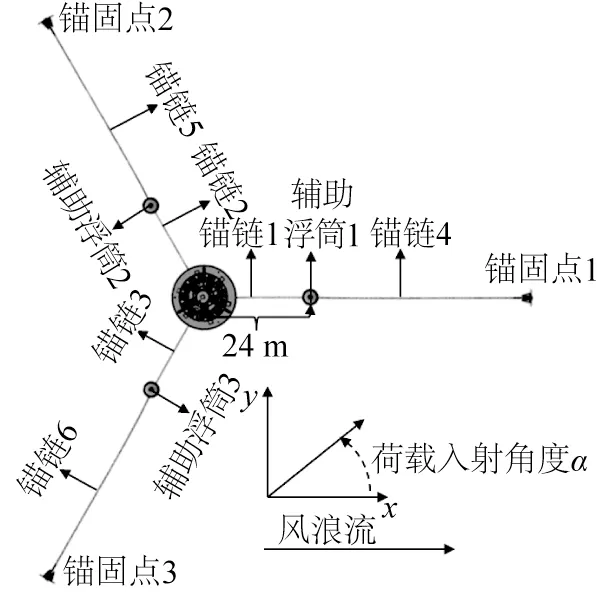
图3 三锚系浮标锚泊系统坐标示意Fig.3 Coordinate diagram of three-anchor buoy mooring

2 浮标水动力性能

2.1 初稳性分析

良好的初稳性可保证倾斜的浮标恢复至平衡位置，初稳心高度是衡量浮标初稳性好坏的重要指标［26］。浮标初稳心高度H计算公式为：

式中：Zb为浮心垂向坐标，Zg为重心垂向坐标，Zs为稳心垂向坐标，r为小倾角下稳心半径，IX为浮体水线处横截面积对其形心X轴的面积惯性矩，A为浮标在水线处的横截面积，y为水线到x轴的距离，D1是浮标水线处的直径，V为浮标的排水体积。通过计算可得浮标的初稳心高度为7.042 m，大于海洋浮式结构初稳心高度的规范要求［27］，说明该浮标设计满足初稳性设计要求。

2.2 大倾角稳性分析

大倾角稳性可用来判断浮标所能承受的极限荷载，计算其丧失稳性后倾覆的极限横倾角度。开展了浮标大倾角稳性校核，浮标的静稳性臂和动稳性臂分别按式（7）、（8）进行计算：

式中：l为静稳性力臂，ld为动稳性力臂，θ为静力矩上限角，φ为变量倾角，Iφ为吃水线面积对转动轴的惯性矩，ηθ为水线面浮心距与纵剖面相交轴距离，a为重心与浮心的距离，V为排水体积，V1为入水体积，V2为出水体积。

图4 为浮标的静稳性臂和动稳性臂曲线，如图所示，浮标的静稳性消失角为95°，在横倾角φ=30°处的静稳性臂为2.07 m，最大复原力臂对应的横倾角为29°，满足相关规范的设计要求。

图4 浮标稳性力臂曲线Fig.4 Buoy stability arm curve

2.3 水动力性能分析

采用频域分析方法分析了浮标结构的水动力特性，研究了浮标水动力性能的变化规律。图5 表示浮标纵荡、垂荡、横摇与艏摇的RAO 值、辐射阻尼及附加质量随波浪周期的变化曲线。

图5 浮标水动力性能变化特性Fig.5 Hydrodynamic performance of buoy

如图5所示，波浪入射角度对垂荡与艏摇RAO 值影响较小，除入射角度α=90°工况外，浮标纵荡RAO 值均随波浪周期的增大而增大，当α=90°时，纵荡RAO幅值接近于0。浮标垂荡RAO值随着波浪周期的增大呈现增大后趋于稳定的趋势。入射角度对横摇响应影响较大，当α=45°、90°、135°时，横摇RAO 值呈先增大后减小的趋势，在T=3 s处达到峰值。随着波浪周期的增大，浮标纵荡、垂荡、横摇和艏摇辐射阻尼均呈现先增大后减小的趋势。纵荡和横摇附加质量随着波浪周期的增大呈现先增大后减小的趋势，在T=5 s 处达到最大。当T≥2 s时，垂荡和艏摇附加质量随着波浪周期的增大逐渐增大，最后趋于稳定。

3 三锚系浮标与锚泊系统运动响应特性

3.1 入射角度对浮标运动响应特性的影响

这里开展了极端海况下不同入射角度对三锚系浮标运动响应特性的影响研究。布放海域的具体海洋环境参数［28-30］如表2所示，极端工况选取风速为45 m/s，表层流速为2.0 m/s，波浪频谱采用Jonswap谱，有效波高为9.1 m，谱峰周期为14.2 s，谱峰因子取3.3。风浪流荷载方向取最危险的同向工况，入射角度α取0°～180°。图6表示不同入射角度下浮标的6自由度运动响应最大值分布。如图6所示，当入射角度为α=0°和α=180°时，浮标在纵荡方向上运动位移显著增大，运动最大值分别达到了14.6 m 和15.3 m；当α=90°时，纵荡运动位移较小。与纵荡方向相反，当入射角度为α=0°和α=180°时浮标在横荡方向上的位移较小，而当α=90°时，横荡方向上的运动位移则达到了14.8 m，与入射角度α=0°和α=180°时浮标纵荡方向的运动最大值相近。浮标横摇运动旋转角度最大值在α=90°明显大于纵摇方向，最大值为21.1°，而纵摇运动在α=0°和α=180°时最大值明显大于横摇方向，最大值分别为16.3°和21.7°。纵荡和横荡、纵摇和横摇受到荷载入射角度的影响较大，当运动方向与环境荷载入射方向一致时，受到荷载的影响其运动最大值相对于其他入射角度显著增大；而垂荡和艏摇运动因与波流环境荷载作用不在同一平面，受入射角度的影响较小，垂荡最大值在α=180°时达到最大值9.1 m。

表2 海洋环境条件Tab.2 Ocean environmental conditions

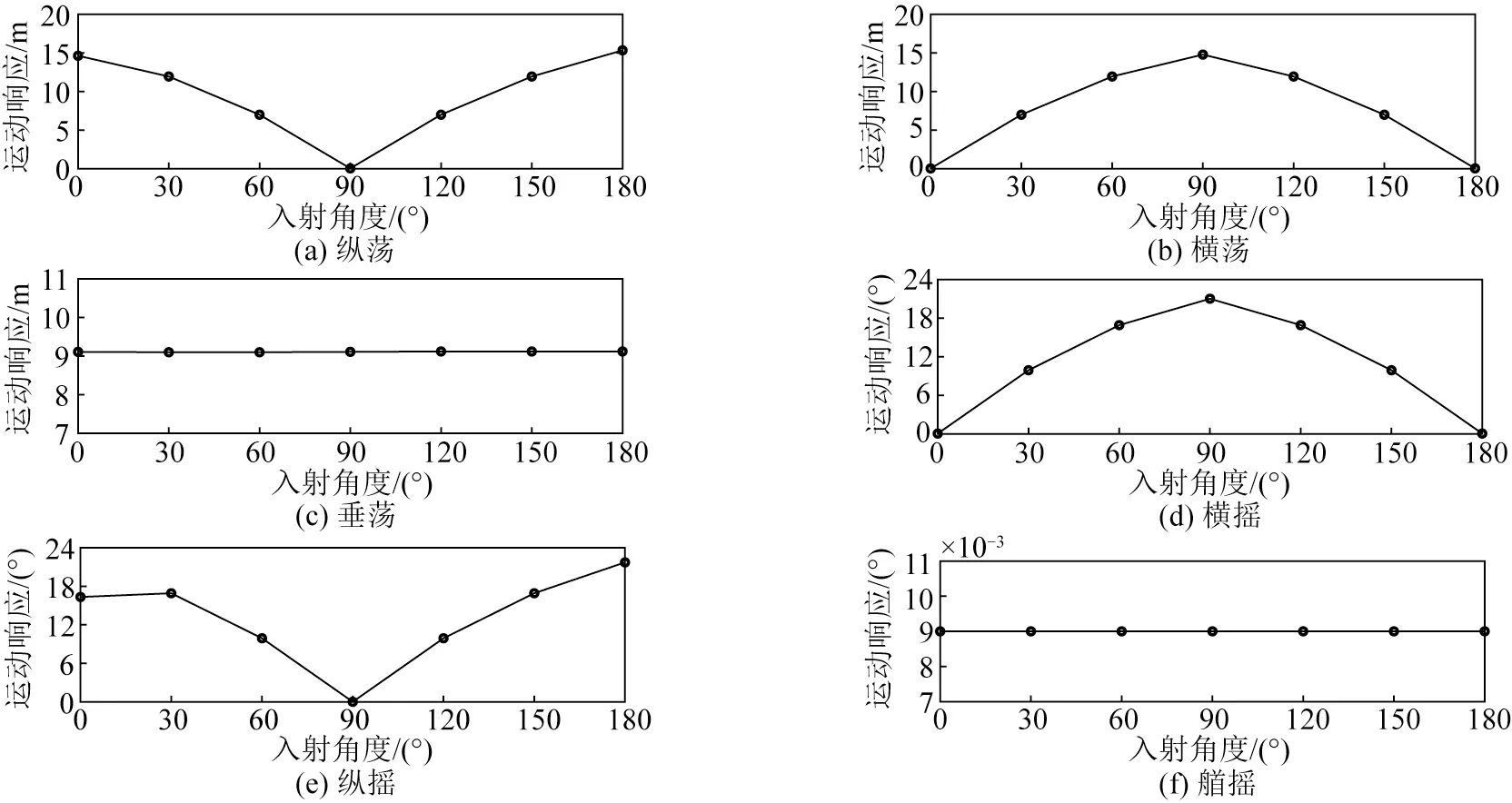
图6 不同入射角度下浮标运动响应最大值Fig.6 Maximum value of buoy motion response at different angles of incidence

3.2 波浪要素对浮标运动响应特性的影响

开展不同波浪要素下浮标6自由度运动响应特性研究。取风、浪、流同向，α=180°角入射，风速和流速分布均保持不变，具体海洋环境波浪参数如表3所示。波浪频谱取Jonswap谱，有效波高4 m≤Hs≤9.1 m，谱峰周期14.2 s≤Tp≤16.7 s，谱峰因子均取3.3。图7 为不同有效波高工况下浮标6 自由度运动响应最大幅值变化曲线（谱峰周期14.2 s）。通过分析可知，当有效波高Hs从4 m 增大为9.1 m 时，浮标6自由度运动响应最大幅值均逐渐增大。由于风浪流环境荷载入射方向与纵荡方向一致，浮标纵荡运动幅值变化较大，当Hs=9.1 m 时，纵荡运动最大幅值达到15.33 m，纵摇运动最大幅值达到21.7°。随着有效波高的增大，浮标垂荡运动最大幅值从3.7 m（Hs=4 m）逐渐增大至9.1 m（Hs=9.1 m）。由于浮标横荡和横摇运动与风浪流环境荷载方向垂直，其运动幅值相对较小，艏摇运动在三锚系的约束下，其幅值也相对较小。

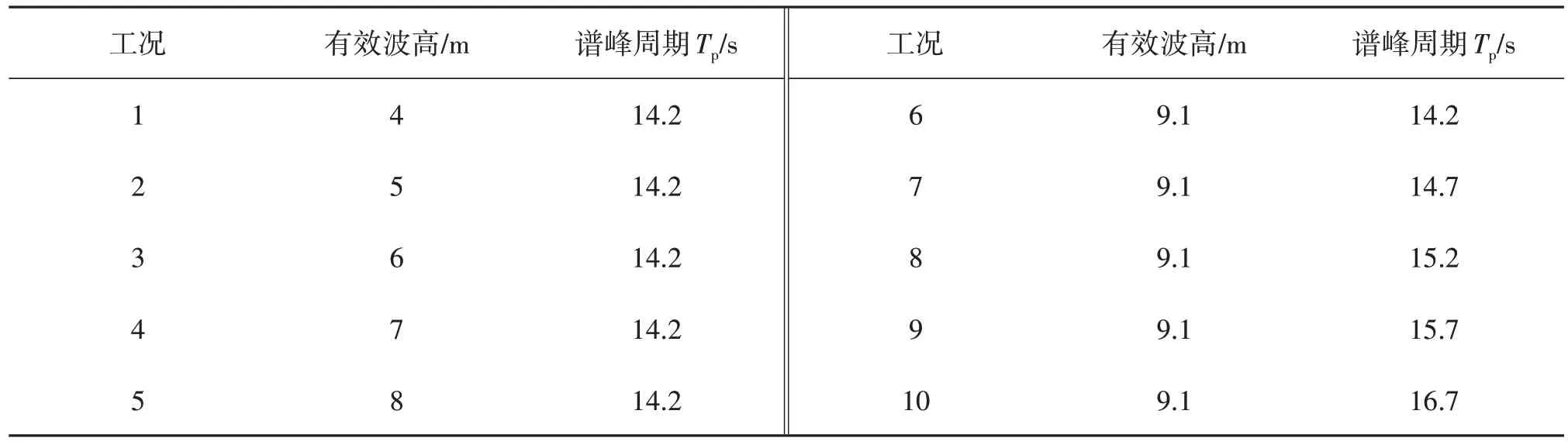
表3 海洋环境波浪参数Tab.3 Variation of wave parameters

图7 浮标运动响应最大值随有效波高的变化曲线Fig.7 Variations of maximum values of buoy motion responses with significant wave heights

图8 为浮标6 自由度运动响应最大幅值随谱峰周期变化曲线（有效波高9.1 m）。当14.2 s≤Tp≤16.7 s 时，随着波浪谱峰周期的增大，浮标的纵摇运动最大幅值逐渐减小，在Tp=14.2 s时达到最大值21.7°，当Tp=16.7 s时，纵摇运动最大幅值减小为14.7°。与纵摇运动相似，浮标横摇运动最大幅值也随波浪谱峰周期的增大而减小。纵荡与横荡运动受波浪谱峰周期的影响较小，随着谱峰周期的增大，两者的运动响应最大值增幅较小，当Tp=14.2 s时，浮标纵荡运动最大幅值为15.3 m，当Tp增大为16.7 s时，纵荡运动最大幅值增大至16.9 m。浮标的垂荡和艏摇运动响应受波浪谱峰周期的影响较小，随着谱峰周期的增大，垂荡和艏摇运动最大幅值分别基本保持在9.1 m和0.009 1°。

图8 浮标运动响应最大值随谱峰周期变化曲线Fig.8 Variations of maximum values of buoy motion responses with peak wave periods

3.3 入射角度对浮标锚泊张力特性的影响

这里开展了极端海况下不同入射角度对三锚系浮标锚链张力特性的影响研究。图9为极端工况下6根锚链张力最大值随风浪流入射角度的变化曲线，如图所示，当入射角度与锚链处于同一平面时，锚链张力最大值明显增大，当α=0°和α=180°时，锚链1和4处于迎浪向，锚链张力最大值明显大于锚链2、3和锚链4、5两组4根锚链。锚链1的张力最大值从α=0°时的17.3 kN减小至α=180°时的12.4 kN，而锚链4的张力最大值从α=0°时的90.2 kN 增大为α=180°时的118.3 kN。当α=120°时，锚链2 和5 接近荷载入射方向，张力最大值明显大于其余4根锚链，张力最大值分别为12.2 kN和97.6 kN。当α=60°时，锚链3和锚链6处于迎浪向，锚链6的张力最大值显著增大，明显大于锚链4和锚链5，锚链3和6的张力最大值分别为11.3 kN和103.8 kN。当α=90°时，锚链2、3、5 和6 接近荷载入射方向，其张力最大值明显大于锚链1 和锚链4。通过对比分析，当风、浪、流荷载与锚链呈同一平面入射时，锚链的张力最大值明显增大，处于侧浪向的锚链张力最大值相对较小。当α=180°时，锚链4张力值最大，其安全系数为9.89，大于中国船级社CCS规范规定的安全系数1.67，符合相关规范要求。

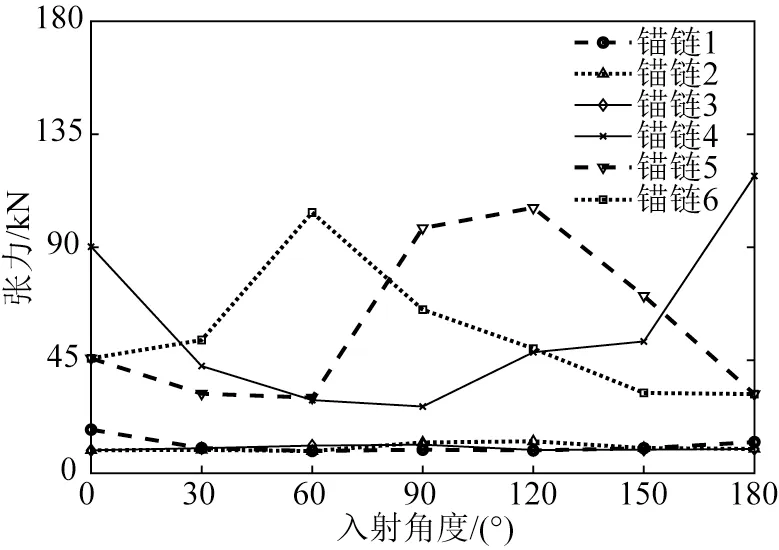
图9 不同入射角度锚链张力最大值变化曲线Fig.9 Variation of maximum mooring tension with different incident angles

通过对比分析，当风、浪、流荷载与锚链呈同一平面入射时，锚链的张力最大值和平均值明显增大，处于侧浪向的锚链张力最大值和平均值相对较小。

3.4 波浪要素对浮标锚泊张力特性的影响

开展不同波浪要素参数下三锚系浮标系统系泊锚链张力特性研究，海洋环境参数工况如表3所示，波浪频谱取Jonswap 谱，有效波高4 m≤Hs≤9.1 m，谱峰周期14.2 s≤Tp≤16.7 s。图10 为浮标系泊锚链张力最大值随有效波高的变化曲线（谱峰周期14.2 s）。如图10所示，随着有效波高的增大，6根锚链张力最大值逐渐增大。由于锚链4 处于迎浪向，当Hs=9.1 m 时，锚链4 张力最大值达到118.3 kN。同处于迎浪向的锚链1，随着有效波高的增大，其张力最大值也随之增大，当Hs增大为9.1 m 时张力最大值达到最大14.3 kN。锚链2、3、5 和6处于侧浪向，随着有效波高的增大，其张力增大幅度与锚链1和4相比较小。当Hs=9.1 m时，锚链4锚泊张力最大，为118.3 kN，其安全系数为9.89，大于CCS 规范规定的安全系数1.67，6 根锚链锚泊张力均满足规范要求。

图10 不同有效波高工况锚链张力最大值变化曲线Fig.10 Variation of maximum mooring tension with different significant wave heights

图11 为浮标系泊锚链张力最大值随谱峰周期的变化曲线（有效波高9.1 m），如图所示，6 根锚链的张力均值随波浪谱峰周期Tp的增大变化较小。当14.2 s≤Tp≤16.7 s时，锚链4、5和6出现明显的极端张力，随着谱峰周期的增大，锚链1、2极端张力基本保持不变，而锚链4极端张力变化较大当Tp＞15.7 s时，锚链4张力最大值显著增大，且当Tp=16.7 s 时张力最大值达到213.2 kN。对比锚链4、5 和6 张力最大值变化可知，随着谱峰周期的增大，浮标的纵荡响应逐渐增大，纵摇响应减小，锚链4 的张力最大值相对于锚链5 和6 会急剧增大。锚链5 和6 的张力最大值随着谱峰周期增大逐渐增大，但是由于处于侧浪向，锚链5 和6 张力最大值和均值变化较小，当Tp=16.7 s时锚链5和6张力达到最大值，分别为39.8 kN和39.7 kN。当Tp=16.7 s时，6根锚链中，锚链4张力值最大，为213.2 kN，其安全系数为5.48，大于CCS规范规定的安全系数1.67，6根锚链锚泊张力均满足规范要求。

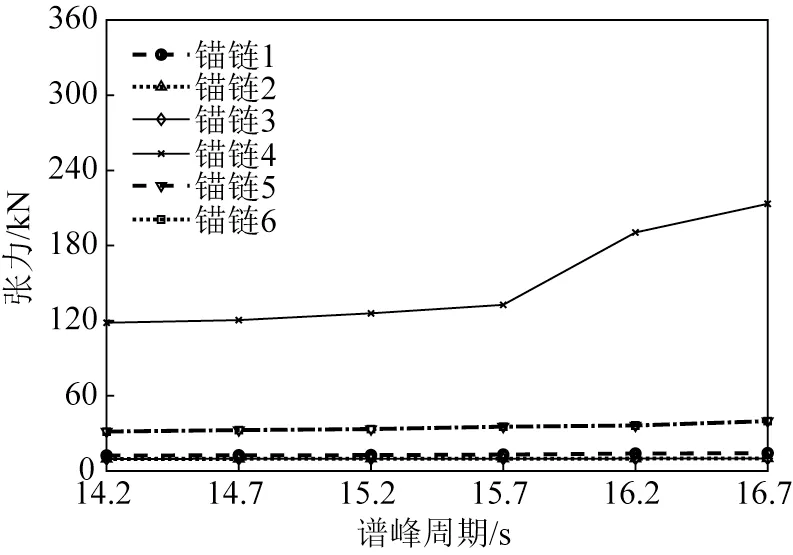
图11 不同谱峰周期工况锚链张力最大值变化曲线Fig.11 Variation of maximum mooring tension with different peak wave periods

综上所述，锚链在风浪流环境荷载和浮标运动作用下发生松弛与张紧状态的循环往复变化，在短时间内受冲击作用出现张力急剧增大现象，锚链1和锚链4处于迎浪向，受波浪影响较大，锚链4出现的极端张力远大于其他锚链。

4 辅助浮筒对三锚系浮标系统的影响

4.1 辅助浮筒对三锚系浮标运动响应特性的影响

这里研究了作业工况和极端工况下三锚系大型浮标运动响应变化特性，对比分析了辅助浮筒对浮标运动响应特性的影响。图12 表示有无浮筒的三锚系浮标系统示意。三锚系浮标系统布放海域的具体海洋环境参数如表2 所示，极端工况选取风速为45 m/s，表层流速为2.0 m/s，波浪频谱采用Jonswap 谱，有效波高为9.1 m，谱峰周期为14.2 s，谱峰因子取3.3。风、浪、流荷载方向取最危险的同向工况，入射角度α=180°。

图12 有无浮筒的三锚系浮标系统示意Fig.12 Different mooring modes of the three-mooring buoy system

图13 为作业工况和极端工况下三锚系浮标系统运动响应示意，在作业工况和极端工况下，浮标与辅助浮筒之间均未出现多体碰撞现象。图14～15分别为在作业工况和极端工况下浮标不同自由度运动响应时程曲线，如图所示，当α=180°时，浮标纵荡和垂荡运动响应最大幅值较横荡幅值大，纵摇运动幅值较横摇和艏摇幅值大。在极端工况下，浮标6 自由度的运动响应最大幅值变化较为剧烈，纵荡最大运动幅值可达15.3 m。由于横荡与波浪荷载作用方向垂直，其运动最大幅值较小。随着波高的增大，浮标垂荡运动最大幅值可达9.1 m。浮标纵摇运动受到波浪荷载的影响较大，其运动最大幅值可达21.7°，横摇、艏摇运动最大幅值远小于纵摇。

图13 不同工况三锚系浮标运动响应示意Fig.13 Dynamic responses of three-anchor buoy and auxiliary pontoon under different working conditions

图14 作业工况下三锚系浮标不同自由度运动响应时程曲线Fig.14 Time history curves of three-anchor buoy responses with different motions under working conditions

图15 极端工况下三锚系浮标不同自由度运动响应时程曲线Fig.15 Time history curve of three-anchor buoy responses with different motions under extreme ocean condition

图16 表示作业工况和极端工况有无辅助浮筒情况下浮标运动响应幅值分布，如图所示，无论是在作业工况还是极端工况，增加辅助浮筒的三锚系浮标的6 自由度运动响应最大幅值均小于无辅助浮筒浮标系统工况。在作业工况下，当无辅助浮筒时，浮标纵摇运动幅值最大，最大幅值可达20.9°，其次为垂荡方向，垂荡运动最大幅值为6.1 m，纵荡与垂荡运动最大幅值接近，约为5.1 m。当增加辅助浮筒时，浮标在纵荡、纵摇及垂荡运动幅值分别减小19.7%、17.2%、23.0%。与作业工况相比，浮标在极端工况下各自由度运动幅度均存在显著增大，其纵摇、纵荡、垂荡运动幅值分别增大28.7%、276.4%、98.3%。当增加辅助浮筒时，浮标纵摇、纵荡、垂荡运动幅值分别减小25.4%、273.2%、93.6%。通过对比分析有无辅助浮筒的浮标运动响应可知，增加辅助浮筒后三锚系浮标的运动响应最大值均小于无辅助浮筒工况。

图16 不同工况浮标运动响应最大值Fig.16 Maximum values of buoy motion response under extreme operating conditions

4.2 辅助浮筒对浮标锚泊张力特性的影响

图17表示作业工况和极端工况有无辅助浮筒情况下浮标导缆孔处的锚泊张力最大值分布。如图17所示，在作业工况下，当浮标存在辅助浮筒时，锚链4、5 和6 的锚泊张力最大值分别为12.3、25.5 和25.4 kN，明显小于无辅助浮筒的浮标锚泊张力最大值，分别减小45%、20%和20%。在极端工况下，当存在辅助浮筒时，浮标锚链4、5和6的锚泊张力最大值均小于无辅助浮筒工况，分别减小19%、31%和31%。与作业工况相比，有辅助浮筒的浮标锚链4、5 和6 在极端工况下张力最大值分别增大106、6 和6 kN，由于和荷载处于同一平面，锚链4 的张力最大值增长幅度最大。通过对比有无辅助浮筒的计算结果发现，在作业工况和极端工况下，辅助浮筒可分担与浮标相连的3根锚链张力荷载，减小锚链的张力最大值，降低浮标的运动响应幅度。

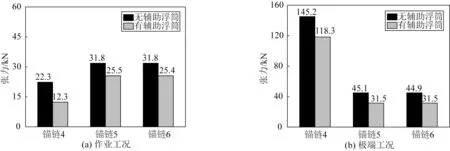
图17 不同系泊方式锚链张力最大值Fig.17 Maximum values of mooring tension forces with and without auxiliary pontoon

为保证辅助浮筒与浮标之间连接的安全性，对辅助浮筒两端系泊系统张力进行了研究，辅助浮筒两端锚链连接示意见图18。如图19 所示，当Hs=4.6 m 时（作业工况），辅助三浮筒A 端的锚链张力最大值分别为9.5、8.9和9.0 kN，B端锚链张力最大值分别为12.3、25.5和25.4 kN，均小于材料破断荷载。当Hs增大到9.5 m时（极端工况），迎浪向辅助浮筒1 的A、B 两端锚链张力变化剧烈，锚链张力最大值迅速增大，A 端张力最大值达到12.8 kN，B 端张力最大值则达到118.3 kN。辅助浮筒2、3 处于侧浪向，两端锚链张力变化相对平稳，辅助浮筒2的A端和B端张力最大值分别为9.7 kN和31.5 kN。综上所述，无论是作业工况还是极端工况，辅助浮筒的运动响应都相对趋于平稳，其两端张力也远小于其材料破断荷载值，可保证辅助浮筒与浮标之间连接的安全性。

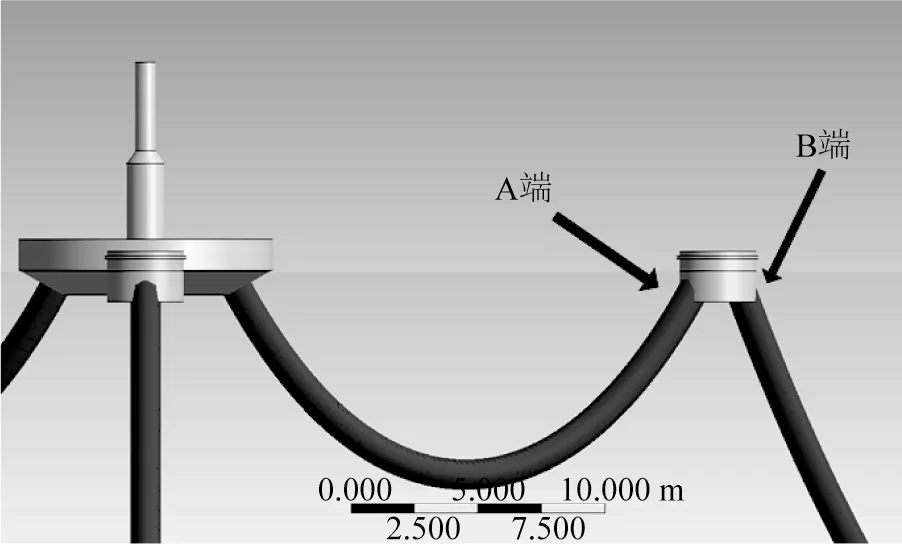
图18 辅助浮筒两端锚链连接示意Fig.18 Schematic diagram of the anchor chain connection at both ends of the auxiliary pontoon

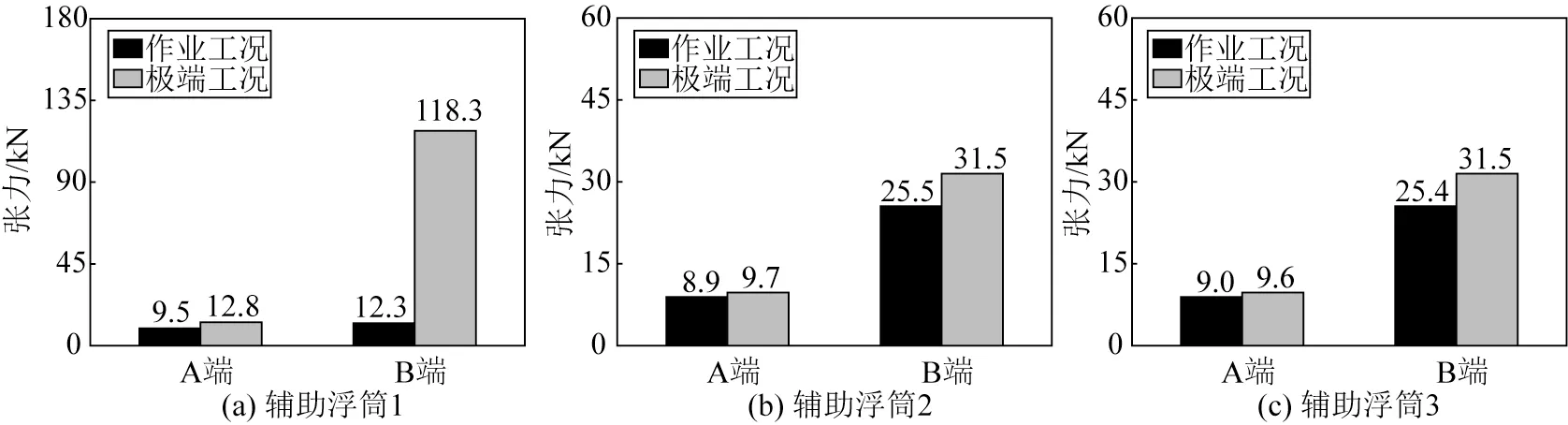
图19 辅助浮筒两端锚链张力最大值Fig.19 Maximum tensions of mooring chain at both ends of the auxiliary pontoon

4.3 辅助浮筒运动响应特性

开展作业工况和极端工况下三锚系大型浮标的辅助浮筒运动响应特性研究。图20 为作业工况和极端工况下辅助浮筒1、辅助浮筒2及辅助浮筒3的不同自由度运动响应最大值分布，如图所示，在作业工况和极端工况下，辅助浮筒的纵荡、垂荡和纵摇运动响应较为明显。在作业工况下，辅助浮筒1、2 和3 的纵荡响应最大值分别为4.9、4.9 和5.0 m，而在极端工况下，辅助浮筒1、2 和3 的纵荡响应最大值分别增大为16.1、15.9和16.0 m。与纵荡运动相反，三浮筒横荡运动响应最大值无明显变化。由于横摇与艏摇运动与荷载入射方向不在同一平面，浮筒横摇和艏摇响应值在风、浪、流荷载的作用下变化较小。在作业工况下，辅助浮筒1、2和3 的纵摇运动响应最大值分别为11.1°、11.7°和11.7°，在极端工况下，分别增大为15.1°、16.2°和16.3°。与作业工况相比，3个辅助浮筒在极端工况下的垂荡最大值增大幅度分别为4.4、4.9和4.9 m。

图20 辅助浮筒运动响应最大值Fig.20 The motion response maximum values of auxiliary pontoon

5 结 语

针对三锚系大型浮标系统开展了水动力与运动响应特性数值研究，揭示了不同波流环境工况下三锚系大型浮标的6 自由度运动响应和锚泊张力变化规律，阐明了辅助浮筒对浮标运动响应和锚泊张力的影响。主要结论如下：

1）由于浮标对称性结构形式，其纵荡和横荡、横摇和纵摇方向的附加质量和辐射阻尼受到波浪的影响差异一致。当T≤5 s，纵荡和横摇附加质量随着波浪周期增大逐渐增大，当T≥2 s，垂荡和艏摇则随着波浪周期的增大而增大。6 自由度的辐射阻尼均随着波浪周期的增大呈先增大后减小的趋势。在同一入射角度下，随着波浪周期的增大，浮标横摇的RAO 值变化较大，呈先增大后减小的趋势，纵荡和艏摇的RAO 值逐渐增大，但是峰值较小，垂荡受波浪周期的影响较小，表明浮标结构设计避开了所在海域的主要波浪周期，避免发生共振。

2）浮标迎浪向的锚链张力大于逆浪向的锚链张力变化，当风、浪、流环境荷载入射方向与锚链处于同一平面时，锚链发生松弛与张紧循环变化，锚链张力短时间内急剧增大，影响锚泊系统的疲劳寿命和浮标安全运维。连接浮标与辅助浮筒的锚链段极端张力受波高变化影响较小，锚链张力最大值远远小于其破断荷载，而连接辅助浮筒与锚体的锚链段受波高变化影响较大，随着有效波高增大，锚链极端张力幅值与出现频次均显著增加；随着波浪谱峰周期增大，锚链极端张力幅值与出现频次也显著增加。

3）在作业工况和极端工况下，辅助浮筒运动响应较小，两端锚链张力最大值远小于破断值；辅助浮筒对三锚系浮标系统的运动响应和锚泊张力存在一定影响，当存在辅助浮筒时，浮标的6自由度运动响应均小于无辅助浮筒的运动响应，各锚链张力最大值小于无辅助浮筒的工况。