深水脐带缆结构阻尼的数值与试验研究
金 川,曹家瑞,李孙伟,陈 凯,俞国军
(1.清华大学深圳国际研究生院,广东 深圳 518055;2.宁波东方电缆股份有限公司,浙江 宁波315801)
深水动态脐带缆是深海油气开发系统的关键结构,被称为海洋油气生产系统的“神经生命线”[1],其内部单元主要包括电缆单元、光缆单元、化学药剂管等功能单元以及聚合物保护层和填充物等结构单元[2]。其中,电缆单元主要为水下生产系统提供电力,光缆单元主要起到传输数据的作用,而化学药剂管是传输化学药剂的通道[3]。动态脐带缆作为连接水上生产系统与水下设备的细长柔性结构物,在运行期间始终受到海洋荷载的作用[4]。特别是海流的作用下,脐带缆两侧会形成交替的漩涡,漩涡脱落则会引起脐带缆结构产生周期性的振动,这种现象被称为涡激振动,是造成动态脐带缆疲劳的主要原因之一[5]。现有研究脐带缆涡激振动响应的方法主要有试验方法、计算流体动力学方法以及经验模型方法。
在经验模型中,尾流振子模型是最为典型的,因其能够很好地预测圆柱体的涡激振动而被广泛运用。首次建立尾流振子模型的学者是Bishop 和Hasson[6],紧接着Hartlen 和Currie[7]将改进的Van Der Pol 方程与结构的振动方程联合求解,用于预测立管的振动。此后,国内外学者对尾流振子模型开展了大量的研究,提出了不同的尾流振子方程和耦合项[8-10]。目前,最常用的模型是将结构的方程与Facchinetti 等[8]提出的尾流振子方程耦合起来。而有研究表明[11-13]:结构方程中的阻尼项会对尾流振子模型的预测准确性造成影响。但是,现有尾流振子模型的阻尼比取值过于保守,小于脐带缆的真实结构阻尼值[14]。
为获得脐带缆真实的结构阻尼,国内外学者开展一系列的试验研究。Fang 和Lyons[14]对脐带缆进行了原型试验,发现脐带缆的阻尼由各单元结构之间滑动引起的库仑阻尼占主导地位。虽然这些测试都为脐带缆结构的设计提供了参考,但是在实际工程中,真实脐带缆的长度更长,并且还受到较大的张力作用,其结构阻尼会受到各种环境因素的影响而改变。根据Fang 和Lyons[15]的研究,脐带缆阻尼在张力的作用下会降低。因此,开展长度更长的脐带缆结构阻尼的研究很有必要。原型脐带缆的海上试验虽然能获得比较直观、真实的数据,但是试验成本高,并且对于长度超过百米的脐带缆开展原型试验显然不现实。数值模型计算方法可以计算复杂弯曲立管结构以及涉及大变形、层间接触模型、变摩擦系数等非线性问题,能够实现超长脐带缆模型的运动模拟。国内外学者们用有限元软件建立了脐带缆三维有限元模型,模拟了构件间的摩擦行为,获得了不错的模拟效果,验证了有限元计算结果的正确性[16-18]。利用数值模拟(有限元)的方法,能够进行脐带缆阻尼的模拟,同时能够进行不同材质和不同摩擦效果的脐带缆运动响应的模拟,对脐带缆的阻尼可以进行较为准确的估计,但是现有的有限元模拟在验证有限元准确性时通常是与理论分析计算的结果进行对比,而未通过试验验证。但是大多理论分析方法都忽略了脐带缆构件间摩擦的影响,这导致采用理论分析的阻尼计算结果不够准确。通过开展脐带缆原型试验获得脐带缆阻尼的真实值,用于验证有限元模型的准确性,使其更具说服力。
因此,文中首先分析了脐带缆结构阻尼的组成和不同参数对脐带缆阻尼的影响以及结构阻尼的试验方法。随后利用ANSYS建立了脐带缆的三维有限元模型并对其结构阻尼进行分析,研究其内部单元的接触对结构阻尼的影响。最后介绍了脐带缆的原型试验,利用自由振动衰减法测出了原型的结构阻尼比,并与有限元模型的结果进行了对比和误差分析,验证了模型的准确性。
1 理论分析
阻尼可以看作是每个振荡周期系统消耗的能量,在动态分析中,阻尼通常表示为每个周期耗散的能量与系统中总能量的比值,而不是耗散的能量本身[19]。在强迫振动中,该比值可表示为损耗因子或阻尼比。这里将对损耗因子进行阐述,分析不同参数对脐带缆阻尼的影响。同时,介绍了结构阻尼的计算方法:自由振动衰减法。
1.1 简谐激励下等效模态损耗因子
脐带缆受到简谐振动时的结构模态阻尼可以用等效滞后阻尼损耗因子表示,其定义为[14]:
以柔性脐带缆为例可以更好地理解等效模态损耗因子。与柔性脐带缆的库仑阻尼相比,空气流体阻尼可以忽略不计。因此,在分析脐带缆的结构阻尼比时只用考虑材料阻尼和库仑阻尼。根据Fang 和Lyons[14]的推导:脐带缆结构阻尼的影响参数包括单元结构的材料阻尼、构件间的库伦阻尼、振幅An以及模态数n。因此,在进行脐带缆有限元模拟时应设置合理的材料阻尼值以及层间摩擦系数等参数,才能保证模拟的准确性。
1.2 自由衰减
结构的阻尼特性无法通过计算得到,用试验的方法确定适当的阻尼比常被用来表示结构阻尼。常用的试验方法为自由振动衰减法[20]。
自由振动衰减法是通过测量结构自由振动时相隔m周期的两个位移幅值之比来确定结构的阻尼比,计算公式如下:
式中:δm= ln (yn/yn+m)为m周期后的对数衰减率,ω、ωD分别为无阻尼和有阻尼时结构的振动频率。当结构阻尼比较小时,式(2)可近似为:
2 脐带缆有限元模型的建立
为明确真实工程中的脐带缆阻尼状态以及影响脐带缆结构阻尼的主要因素,以中国南海某深水油气开发项目的钢管脐带缆为研究对象,根据其几何尺寸和材料参数,利用ANSYS 建立有限元模型并对脐带缆的结构阻尼进行分析。
2.1 脐带缆几何尺寸
试验选择的脐带缆主要由中心钢管、螺旋缠绕的功能构件、外层聚合物护套与内部填充材料组成,表1给出了各构件的几何尺寸,脐带缆截面如图1所示。

图1 脐带缆截面Fig.1 Umbilical section design drawing

表1 脐带缆构件几何尺寸Tab.1 Geometric dimensions of umbilical components
脐带缆中库伦阻尼主要来自各螺旋单元之间、螺旋单元与外层护套之间、主要构件与内部填充之间的相互摩擦。基于此,文中模拟忽略其内部结构对结构阻尼的贡献,在保证简化前后结构整体力学性能(如质量、刚度)不变的前提下,将电缆单元等效为外部为聚合物、内部为铜的双层管状结构。
2.2 脐带缆材料属性
脐带缆模型中各构件的主要材料为超级双相不锈钢、聚合物材料、填充物橡胶以及电缆单元内部的铜。在进行其内部结构阻尼分析时,采用单一的线弹性模型,表2给出了各材料参数取值。

表2 脐带缆材料属性Tab.2 Umbilical material properties
2.3 脐带缆有限元模型
为了探究脐带缆内部各构件间接触作用的影响,基于ANSYS 软件,选用高阶3D20 节点和Solid186 实体单元进行各个构件的模拟,建模时内部螺旋构件螺距为3 m。采用扫掠的方式生成网格,划分网格后的脐带缆有限元模型如图2所示。
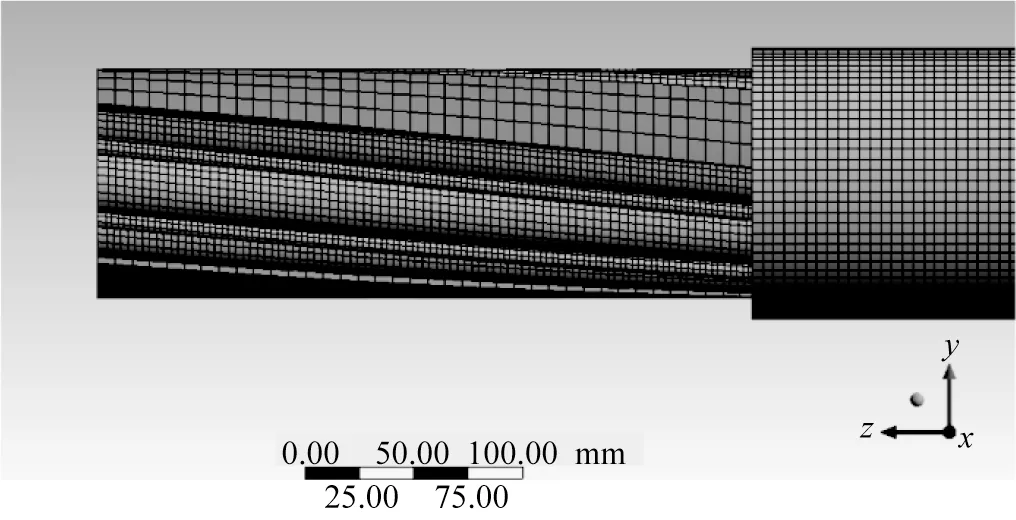
图2 脐带缆模型Fig.2 Umbilical model
接触界面存在于中心钢管之间、中心钢管与各功能单元护套之间、功能单元钢管与聚合物护套之间、各功能单元护套之间、各功能单元护套与外层护套之间以及各构件与填充物之间,均设置为摩擦接触,模型中接触面共65对,表3给出了各接触面材料之间的摩擦系数。

表3 各材料间的摩擦系数Tab.3 Friction coefficient between materials
在设置接触时,在两个构件之间选择较刚的面作为目标面,聚合物护套之间选择对称接触形式(即一个面既为接触面又为目标面)。
进行有限元分析前,将脐带缆一端各构件截面的自由度完全约束,另一端截面上所有节点自由度耦合。并在自由端的y方向施加了大小为36 mm的初始位移,在开始的时间节点抑制位移载荷进行释放,使脐带缆模型进行自由衰减振动。
利用ANSYS Workbench 进行分析,即可得到脐带缆模型中距离固定端1.2 m处(原型试验中的测点1)和2.4 m处(原型试验中的测点2)自由衰减振动的位移响应,结果如图3所示。
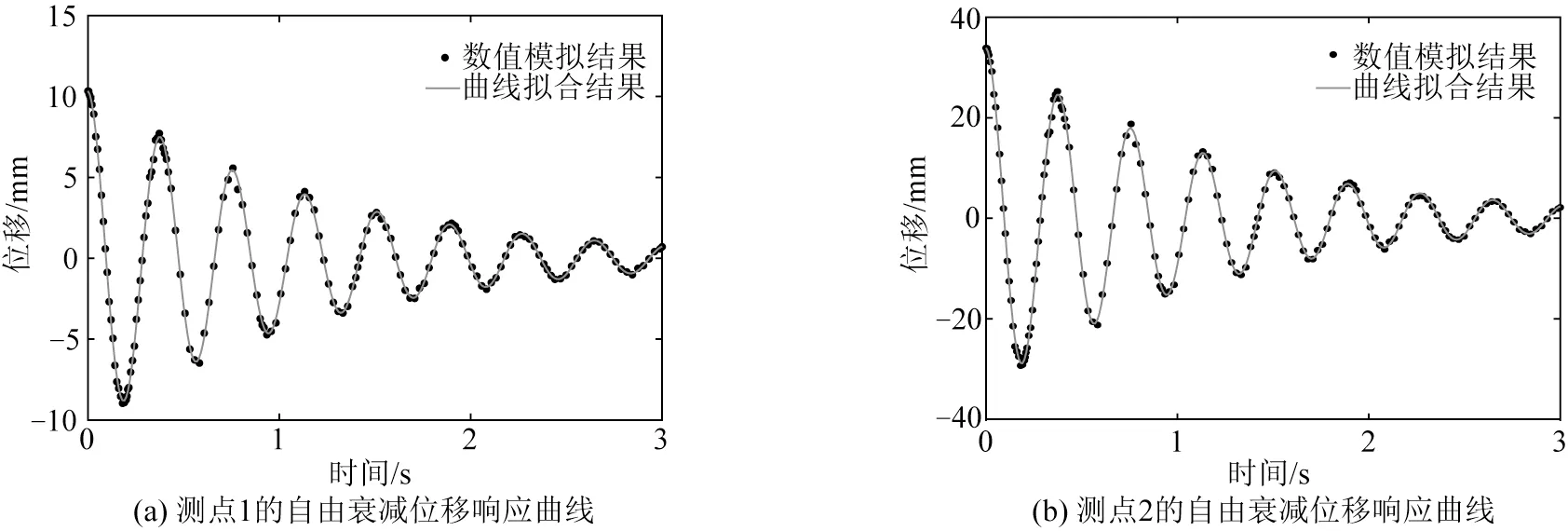
图3 脐带缆有限元模型数值模拟结果Fig.3 Numerical simulation results of umbilical cable finite element model
通过Matlab 拟合得到测点1 的位移响应曲线为x= 10.355 cos (16.6t)exp(-0.846t),计算可知,该脐带缆模型的振动周期为0.376 s,阻尼比为0.051。测点2 的位移响应曲线为x= 33.898 cos (16.6t)exp(-0.844t),振动周期为0.376 s,阻尼比为0.051。
3 脐带缆原型测试
为获得脐带缆结构较为真实的阻尼值以及振动周期,利用自由振动衰减法对用于中国南海某深水油气开发项目的钢管脐带缆开展了原型试验。
3.1 测试装置及步骤
钢管生产公司提供了长2.5 m、直径0.12 m的钢管脐带缆原型试件用于测试脐带缆的结构阻尼值。该脐带缆实际用于中国南海某深水油气开发项目,是该项目的实际备件。为了固定脐带缆进行自由振动衰减的测试,特意制作了一套牢固的夹具,用于固定脐带缆以及尽可能减小端部摩擦对结构阻尼测试的影响。图4给出了试验现场的照片。

图4 脐带缆试件及固定装置Fig.4 Umbilical cable test piece and fixing device
试验采用的是自由衰减法。试验前先利用夹具将脐带缆的一端固定,并在脐带缆上布置了2 个小灯泡作为测量标记点,测点1 距离固定端1.2 m,测点2 距离固定端2.4 m。试验时,先打开SMT-3D(非接触)三维动态位移测量系统,等待位移曲线平稳后,利用工程锤垂直向下敲击脐带缆自由端上部的中间位置,使其发生竖直向下的初始位移,等2个测点位移变为零且平稳后再停止记录。图5给出了测试系统的示意。

图5 测量系统示意Fig.5 Umbilical layout diagram
试验中用到的SMT-3D(非接触)三维动态位移测量系统是利用原创的、具有国际领先水平的快速、高精度亚像素定位算法(subpixel registration algorithm)对高速数字相机视频图像中多个被测点的运动轨迹进行实时、高精度跟踪,可获得外载荷作用下被测点(亚像素精度的)x/y/z三个方向的位移量。其位移精度为:±0.01 mm(x、y值、5 m距离),±0.05 mm(z值,5 m距离)。
此次SMT-3D(非接触)三维动态位移测量系统的采样频率为50 Hz,试验时实际采样频率为5 Hz大于两倍结构自振频率,符合采样要求。试验一共进行了10次,为减小端部夹具与脐带缆摩擦造成的影响,选取前5次测试中的振动幅值较小、振动曲线最完整的结果作为此次试验结果,进行脐带缆的阻尼计算。
3.2 测试结果
利用SMT-3D(非接触)三维动态位移测量系统测得脐带缆测点1 和测点2 的自由衰减位移响应曲线如图6所示。
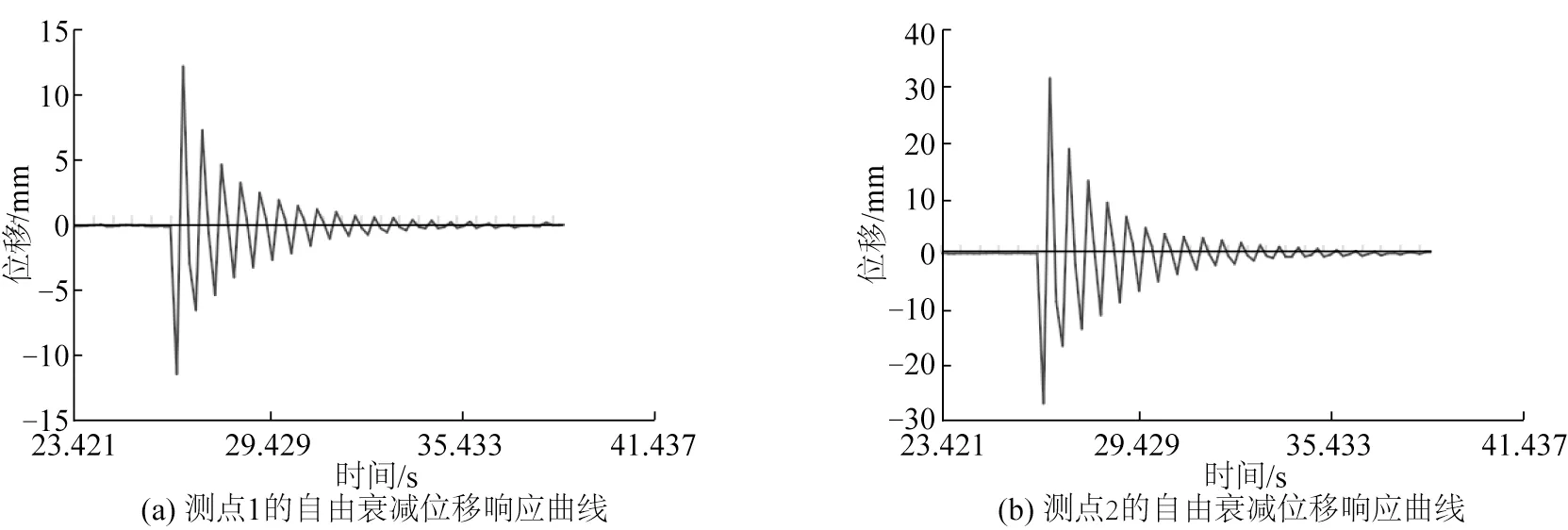
图6 测点的自由衰减位移响应曲线Fig.6 Free attenuation displacement response curve of test point
自由衰减法获得的结构阻尼比往往依赖于所取的振幅。为了获得更加精确的阻尼比,将测试得到的测点1 和测点2 的振动数据利用Matlab 进行拟合,拟合时采用fittype 构造自定义函数,自定义函数的形式为结构自由衰减的指数表达式。图7给出了这两点的自由振动衰减曲线拟合结果。

图7 拟合结果Fig.7 Numerical fitting results
测点1通过Matlab 拟合得到脐带缆位移响应曲线为:x= 11.42 cos (10.18t)exp(-0.563 4t)。计算可知,响应曲线的周期为0.616 s,阻尼比为0.055。测点2 通过Matlab 拟合得到脐带缆位移响应曲线为:x=29.7 cos (10.18t)exp(-0.560 3t)。计算可知,振动周期为0.616 s,阻尼比为0.055。
3.3 结果讨论
将实际测量得到的阻尼数值和ANSYS 模拟得到的阻尼数值进行对比后发现,阻尼比的实际测量值与ANSYS模拟得到的值非常接近,相对误差仅为7.27%。这说明ANSYS模拟能够在很大程度上获取脐带缆阻尼的特性,是一个研究脐带缆阻尼的好工具。同时,周期的相对误差非常大,这说明ANSYS模拟存在一定的误差,主要是在开展原型试验时,固定脐带缆的夹具不能保证完全固定,导致脐带缆在试验中会发生滑移和松动,这也导致了试验测得的脐带缆一阶振动周期和阻尼比的值比有限元模拟的值大。
考虑到实际试验中脐带缆端部没有做到完全固定,在原本有限元模型的基础上将端部的固定约束Fixed Support改为弹性约束Elastic Support,图8给出了自由衰减振动阶段的位移响应。
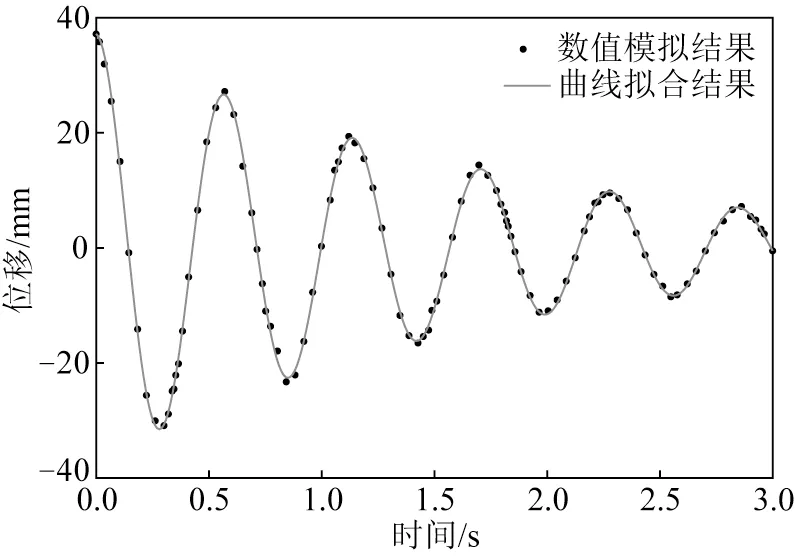
图8 脐带缆有限元模型数值模拟结果Fig.8 Numerical simulation results of umbilical cable finite element model
通过Matlab 拟合得到该位移响应曲线为x= 36.89 cos (11.02t)exp(-0.578 5t),计算可知,该脐带缆模型的振动周期为0.570 s,阻尼比为0.052,端部最大位移为1.03 mm。表4给出了有限元模型模拟结果与原型测试试验结果的相对误差。可以发现在端部没有完全固定的情况下振动周期会有明显增长,更接近原型测试的结果。

表4 数值与试验的误差分析Tab.4 Error analysis of numerical and experimental methods
4 结 语
利用有限元软件ANSYS建立了脐带缆的多层滑移接触摩擦有限元模型,并获得了脐带缆的一阶振动周期和阻尼比。并将结果与该动态脐带缆原型试验获得的值进行了对比,发现文中的有限元模型获得的阻尼值与试验值非常接近。这为将来工程中获得脐带缆阻尼比的值提供了好的方向,既能准确获得真实的脐带缆阻尼比的值,又解决了采用原型试验成本过高这一问题。脐带缆结构阻尼比的值对尾流振子模型关于立管振动的预测结果的准确性较为重要,如果在尾流振子模型中能够采用较为准确的结构阻尼比,预测结果将会更加精确,预测结果对于工程的参考性也就更大。
未来的研究将致力于利用ANSYS 建立实际长度脐带缆的有限元模型,获得其振动状态下的结构阻尼比,并将结果用于对尾流振子模型的改进,从而获得更加准确的预测结果。

