集成于海上风电钢管桩基础上的升降式网箱结构波浪场特性研究

田正林，毛鸿飞，吴光林，赫岩莉，林金波

（广东海洋大学 海洋工程与能源学院，广东 湛江 524088）

随着近岸优良养殖海域的减少，海水养殖逐渐由近海向深海发展，而深远海浪大流急，海况恶劣，给养殖网箱的安装与固定带来了巨大挑战。另外，随着海上风电产业的迅速发展，海上风电基础安装海域逐渐由水深10 m 发展到水深30 m 甚至是更深海域，钢管桩基础是海上风电基础的一种重要结构形式，适用水深为20～50 m，其结构整体性好，刚度大，可承受深海中风、浪、流的巨大冲击作用［1］。近年来，工程师和学者们提出将网箱结构安装在深水钢管桩上，这是解决深水养殖网箱结构安装问题的一种大胆尝试，也是海洋牧场与海上风电项目融合开发的一个重要发展方向，符合国家“陆海统筹”发展的规划目标和“双碳”目标。集成在风电基础钢管桩上的养殖网箱结构可以将波浪、流、风的作用力传递给风电基础结构，以基础结构为固定装置，利用浮架系统、压载水补偿装置和沉子系统使网箱结构在竖向上进行限位升降运动，应对极端海况的侵害。在保障钢管桩基础安全的前提下，将养殖网箱安装于直立钢管桩上可以进一步利用海域优良资源，形成一种风电项目与渔业养殖融合发展的新模态。

传统的浮式网箱结构一般由框架结构、网衣结构和锚固系统3个主要部分组成［2］，深水网箱框架结构是网衣重要的受力载体，网衣受到的水流、波浪等作用将直接作用在网箱框架结构上，框架结构将所受荷载作用到钢管桩上，最终传递到海底基础。网衣是海上养殖网箱结构的重要组成部分，具有维持养殖空间、构建鱼类生境、防止鱼类外逃、防止外界敌害侵袭等关键作用［3］。极端海况下网箱结构内部的流场变化会造成鱼类朝某一方向强烈运动，使得网箱结构产生巨大的倾覆力矩。在深海安装网箱结构时，克服复杂海况对网箱结构的威胁是一个重要挑战，升降式网箱结构在强风暴或极端海况时可以下潜到安全水深，规避侧倾覆危险。黄滨等［4］研究了升降式网箱结构的防倾覆技术，并分析了网箱侧翻的内外影响因素，所得结果对升降式网箱结构的设计及实际应用具有重要指导作用。网箱淹没深度对网箱结构水动力特性及响应特性具有重要影响，王非等［5］采用试验和数值方法研究了淹没深度对网箱结构水动力特性的影响规律。升降式网箱工作中将受到海洋环境条件及自身结构系统组成的影响，其动态变化过程较为复杂，造成倾覆的因素也是多方面的，其中水体的波动是最为突出的一个。而对于安装在钢管桩基础上的升降式网箱结构，由于网箱结构固定于钢管桩上，一般较少发生倾覆事故，但需要控制升降过程中的速度。不同于传统类型的网箱结构，升降式网箱的网衣四周需要固定在坚固的框架结构上，最后固定于钢管桩上，在波浪、水流的作用下，网衣的变形较小［6］，但网衣对水流的作用、流场的影响较大。

网箱结构安装在深海风电钢管桩之上，网箱结构内水体的流动对鱼类的生存环境影响较大，箱体内的流速大小对箱体内水体的交换速度具有重要影响，并决定了适合养殖鱼的种类［7］，且网箱内部及周围的流场特性对结构受力也有重要影响，因此网箱结构对流体的水动力特性影响研究备受关注［8-16］。吴常文等［17］对深水网箱抗风、浪、流性能进行了试验研究，研究发现水流流速主要影响网具系统，而波浪对网箱整体结构有显著影响。由于深海升降式网箱结构的变形较小，在研究网箱结构水动力特性时可忽略网箱的体积变形，而网衣属于多孔柔性结构体［18-20］，孔隙介质结构可以用来模拟网衣对流速的衰减作用［21］。Chen 和Christensen［22］通过多孔介质模型模拟了方形网箱和圆形网箱的阻流作用，分析了网衣周围的流场变化特性，并与试验结果进行了对比。Patursson 等［10］采用孔隙介质模型模拟了水流经过网箱结构的流动情况，Zhao等［23-24］应用多孔介质模型模拟了流体通过网衣的流动，模拟结果通过与试验结果的比对发现具有较好的可信度。Chen和Christensen［25］，Shim等［26］，Cornejo等［27］，Kim等［28］分别采用多孔介质模型数值模拟了网箱与波浪相互作用的流场特性，并进行了相关参数对流场特性影响的分析。多孔介质模型在以往网箱结构水动力特性研究中得到了广泛应用，但在升降式网箱结构波流作用下的三维水动力特性研究中的应用少有报道，在对钢管桩上网箱结构的流场特性研究中及速度分布情况研究中更是匮乏。由于在深海风电钢管桩上安装升降式网箱结构属初步研究阶段，研究成果和应用实例较少，其中涉及到的众多问题需要进一步探讨和解决。

综上，在风电钢管桩基础上安装的网箱结构可以进行垂向升降运动避免复杂海况的影响，且通常钢管桩直径相比于网箱结构水平尺度小得多，在波浪和流的共同作用下网箱结构内部流场主要受到网箱结构的影响。以往研究对网箱结构在波、流共同作用下的内部三维流场特性影响关注较少，而安装于钢管桩基础上的升降式网箱结构在波浪、流等的作用下网箱结构对其内部及周围流场具有重要影响，并且网箱内部流场与网箱结构特性和网箱结构的升降高度有很大关系，其作用机理复杂，罕见报道。文中将基于OpenFOAM 软件包开发波浪与升降式网箱结构相互作用的数值研究模型，采用多孔介质模型模拟网箱结构，优化网衣阻尼特性，研究不同淹没深度下网箱结构的波浪场变化特性，得到网箱结构的最优升降高度范围。所得研究成果将为网箱养殖用户的鱼类品种选择提供参考，为深海钢管桩基础上的升降式网箱结构设计提供借鉴。

1 钢管桩基础上的升降式网箱结构

提出一种安装在风电钢管桩上的升降式网箱结构，其结构形式如图1所示，网箱结构的俯视图如图2所示。升降式网箱结构通过套筒与钢管桩基础连接，网箱结构通过压载水补偿装置进行升降。钢管桩基础上的升降式网箱结构需要在操作工况下提供优良的流场环境，极端工况下克服复杂海况的影响能够下潜至安全的淹没水深，安全淹没深度可以提供正常工况下的流场及保证安全要求。由于试验相对复杂，实施难度较大，考虑到周期和成本，文中拟通过数值计算方法研究安装在风电钢管桩上的升降式网箱结构的流场变化特性。

图1 风电基础钢管桩上的网箱结构Fig.1 Submersible cage structure installed on steel pipe piles

图2 网箱结构俯视图Fig.2 Top view of cage structure

2 数值模型

基于OpenFOAM 平台开发波浪与升降式网箱结构相互作用的数值波浪水槽研究模型，网箱结构采用多孔介质模型模拟，流体模型采用雷诺时均RANS 方程，流体求解方法采用耦合PISO 方法和SIMPLE 方法的PIMPLE方法，研究不同淹没深度下网箱结构的流场变化特性。

目前，有较多的方法模拟孔隙介质流动，但是没有一个普遍的、统一的方法，总体上可以归纳为宏观方法和微观方法两种方法［29］，由于网衣结构无法准确描述结构的几何外形，需要采用宏观的孔隙介质方法模拟网箱结构的孔隙流动，以便更好地理解孔隙介质在流体流动中的全局效应。采用Del Jesus等［30］改进后的模型模拟孔隙介质结构，考虑了孔隙度随时间推移和空间位移的变化效应，孔隙介质内流体流动和孔隙介质外流体运动遵循雷诺时均RANS方程，自由水面通过流体体积法（VOF）进行追踪，详细方程为：

式中：U为速度矢量；n为孔隙度；p为压力；ρ为流体密度：g为重力加速度；μ为动力黏度；α1为流体体积分数；a、b、c为反应材料特性的系数，控制各摩擦项之间的平衡。从形式上可以看出：式（1）～（3），在孔隙介质外孔隙率n为1，忽略孔隙结构阻力后，其为孔隙介质外流体流动方程。

式（2）中的最后3 项分别是模拟层流的线性项［31］、模拟大雷诺数的二次项［31］、代表惯性加速度的非稳态项［32］，通过这3项可以很好地模拟孔隙介质中的流体流动。为了更好地理解式（2），将其进行改写：

式中：A=ρa；B=ρnb。注意式（4）和式（2）除了3 个阻力项后是完全一样的，式中A和B采用Engelund［33］公式，并由Van Gent［34］进行了改进，得到下式：

式中：D50为介质材料的中值粒径；KC为Keulegan-Carpenter 数，引入系统的振荡项和非稳态性，定义为TOuM/(D50·n)，uM为最大振荡速度，TO为振荡周期；摩擦系数α、β需要校正确定，可取为10 000和3［29］。

以上方程需要采用湍流模型进行封闭，采用k-ε模型进行封闭求解流体流动方程［35］。值得注意的是：式中的参数a、b与介质材料有关，需要进行率定确定，文中采用相似孔隙介质结构的经验参数［29，36］，a取50，b取2，c值的变化对大多数情况下的模拟结果影响不大［36-38］，可取为0.34。由于网箱结构透浪透流，波浪反射比较小，因此数值波浪水槽模型左端采用主动吸收边界（给定速度和波面）进行造波，数值波浪水槽模型右端采用主动波吸收系统（吸收波速）进行消波，详细理论及造波消波系统在程序中的具体实施参见文献［37］。

3 模型验证

3.1 造波造流边界验证

为了验证造波边界和消波边界的准确性，建立了无结构物的数值波浪水槽，模拟了水深1.6 m，周期2.1 s，波高0.36 m 时距离造波边界4倍波长处的二阶Stokes 波波面历时曲线，并与理论波形进行对比。数值模拟中比尺选择遵循重力相似准则，模型比尺取为1/25，对应实际海域的波浪条件为：海域水深40 m，周期10.5 s，波高9 m。数值模拟二阶Stokes波波面历时变化曲线见图3，从图3中可以看出：数值模型计算波面与理论波面拟合较好，说明数值波浪水槽造波和消波边界满足要求。

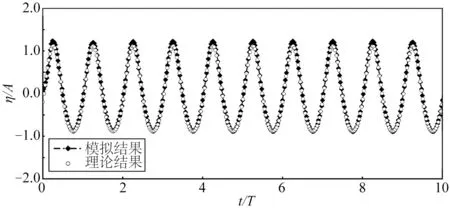
图3 数值计算波面与理论波面历时曲线的对比Fig.3 Comparison of the time series of free surface between simulating and theoretical results

为了验证数值波流水槽的准确性，将波流耦合作用下产生的数值波面结果与He 等［39］数值模拟结果、Umeyama［40］试验数据进行了对比。Umeyama［40］试验所用水槽尺寸为25 m×0.7 m×1.0 m（长×宽×高），左端配有活塞式造波机，右端配有吸波装置，水槽底部可以进行水流的循环，纯流情况下可产生深度平均稳定的流速为0.08 m/s 的流。试验过程中采用的波浪条件为三阶Stokes 波，水深0.3 m，周期1.0 s，波高0.023 4 m，浪高仪距离造波机14 m。数值模拟区域水平向为0 m≤x≤20 m，竖直向为0 m≤y≤0.7 m。网格在x、y方向上平均分布，Δx=0.002 m、Δy=0.001 m。数值模拟15个周期后距离造波边界4倍波长处（x≈18 m）的水面计算结果与试验结果见图4，从图4可以看出，数值模拟水面结果与试验结果基本吻合。

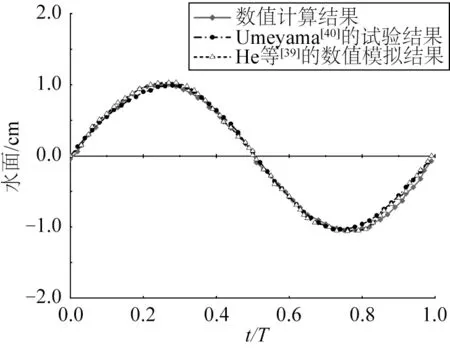
图4 水面的数值计算结果与He等[39]数值模拟结果、Umeyama[40]试验结果的对比Fig.4 Comparison of the computed water surface profiles with the experimental results of He， et al[39] and Umeyama[40]

3.2 流场验证

流场验证前首先需要调整数值模型确定D50和孔隙率的取值，经过调整后D50取0.016 m，孔隙率取0.32。然后以Bi等［41］的网衣试验结果验证数值模型的准确性，以厚度为5 cm 的矩形多孔介质区域模拟网衣，验证所建多孔介质模型可以很好地模拟波浪与网衣作用后的流场。试验过程中采用的水槽尺寸为22 m×0.45 m×0.6 m（长×宽×高），试验水深为0.4 m，网衣固定在0.3 m×0.3 m 的矩形框架上，框架结构为直径6 mm的圆钢材料。试验过程中网衣垂直于试验水槽底部和侧壁，水流垂直作用于网衣结构上，流速采用布置在网衣中心垂直截面上的粒子图像测速仪（PIV）技术进行测量。验证中网衣具体参数见表1，入口水流流速取为0.17 m/s，网衣在水槽中的具体位置见图5。

表1 网衣模型参数Tab.1 The characteristics of the net model

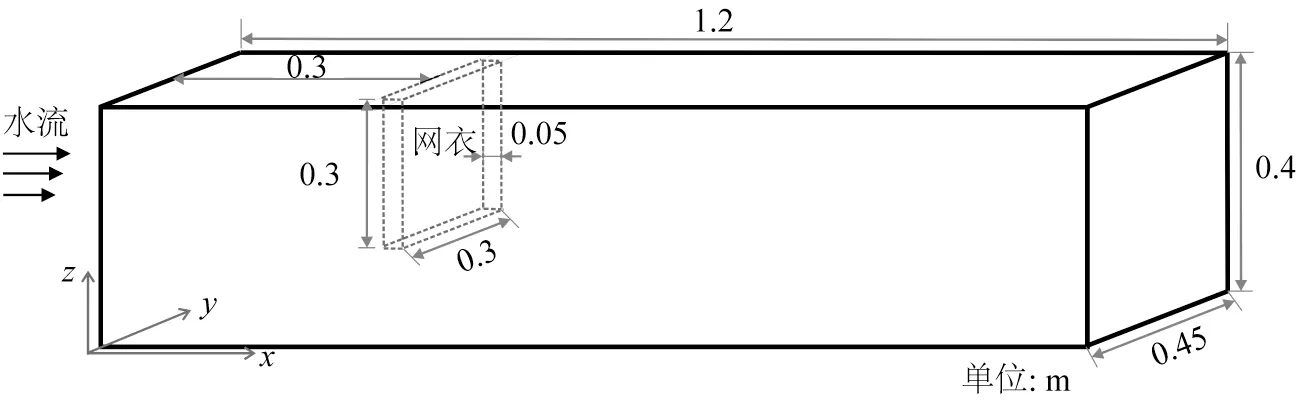
图5 网衣布置Fig.5 The position of net in fluid computational domain

图6为水流流速0.17 m/s，距离网衣背流侧0.15 m处垂向的流速分布曲线。

图6 网衣背流侧0.15 m处z向速度变化曲线Fig.6 Magnitude of current velocity in z direction at 0.15 m on the downstream of net

从图6中可以看出：受网衣阻流效应的影响，网衣背流侧有明显的流速衰减区域，速度有所减小；网衣背流侧0.15 m处流速衰减区域内，水流流速数值模拟结果与朱传之等［42］的仿真结果和Bi等［41］试验结果吻合较好（其平均相对误差分别为4.2%和9.3%），相对平均流速衰减率小于10%，且z方向的流速变化规律相同，说明所建数值模型可以很好地模拟网衣附近的流场变化情况。值得说明的是图6中在z=-300 mm处数值模拟结果与试验结果略有偏差，原因可能是Bi等［41］试验过程中在z=-300 mm处安装有较大阻流作用的直径6 mm的圆钢支架结构。

4 研究条件

4.1 网箱结构参数

文中所考虑升降式网箱结构拟应用于水深30～50 m的离岸外海域。升降式网箱结构需要依附在深水风电钢管桩基础上，钢管桩为4 桩形式，桩距15 m，因此实际海域的网箱结构尺寸为15 m×15 m×12 m（长×宽×高），数值模拟过程中采用的比尺为1∶25，数值模拟的网箱结构尺寸为0.6 m×0.6 m×0.48 m（长×宽×高），网衣线面积系数、目脚直径和目脚长度等参数仍然采用Bi等［41］的网衣模型参数，见表1，多孔介质模型参数D50和孔隙率仍取为0.016和0.32。

4.2 波浪参数

研究海域水深40 m，波浪条件（波高，周期）见表2，其中工况1 代表海域1 年一遇操作工况，工况2 代表海域50 年一遇极端工况。海流条件：工况1 沿深度方向平均流速1.08 m/s；工况2 沿深度方向平均流速1.82 m/s。数值模拟中采用的模型比尺为1∶25，水深D为1.6 m，数值模拟的波浪条件（波高，周期）见表3。

表2 实际海域波浪的极值参数Tab.2 Extreme parameters of waves in practical sea

表3 数值模拟波浪参数Tab.3 Wave parameters in numerical simulation

4.3 研究方案

数值模拟研究中网箱结构被简化为由6 个面网衣组成的三维空间封闭结构，各工况下的网箱结构位置及监测点分布见图7。数值计算中，网箱结构水平方向位置保持不变，只沿垂向进行位置移动，研究网箱结构淹没深度变化导致的流场特性变化规律。

图7 网箱结构及内部测点布置Fig.7 Diagram of the submersible cage structure and the layout of measuring points

5 研究结果与分析

首先研究工况1（操作工况）在波流共同作用下网箱结构内部的流场特性，然后研究工况2（极端工况）在波流共同作用下不同网箱下潜深度的流场变化特性，确定网箱结构极端工况下的最佳下潜深度。

5.1 工况1下的流场特性计算结果与分析

图8 给出了工况1 水深D为1.6 m，波浪周期T=0.9 s，波高H=0.08 m，沿深度方向的平均流速0.216 m/s，网箱结构顶部潜深d=0 m时波浪与网箱结构作用10个周期后第11个周期内的流场。

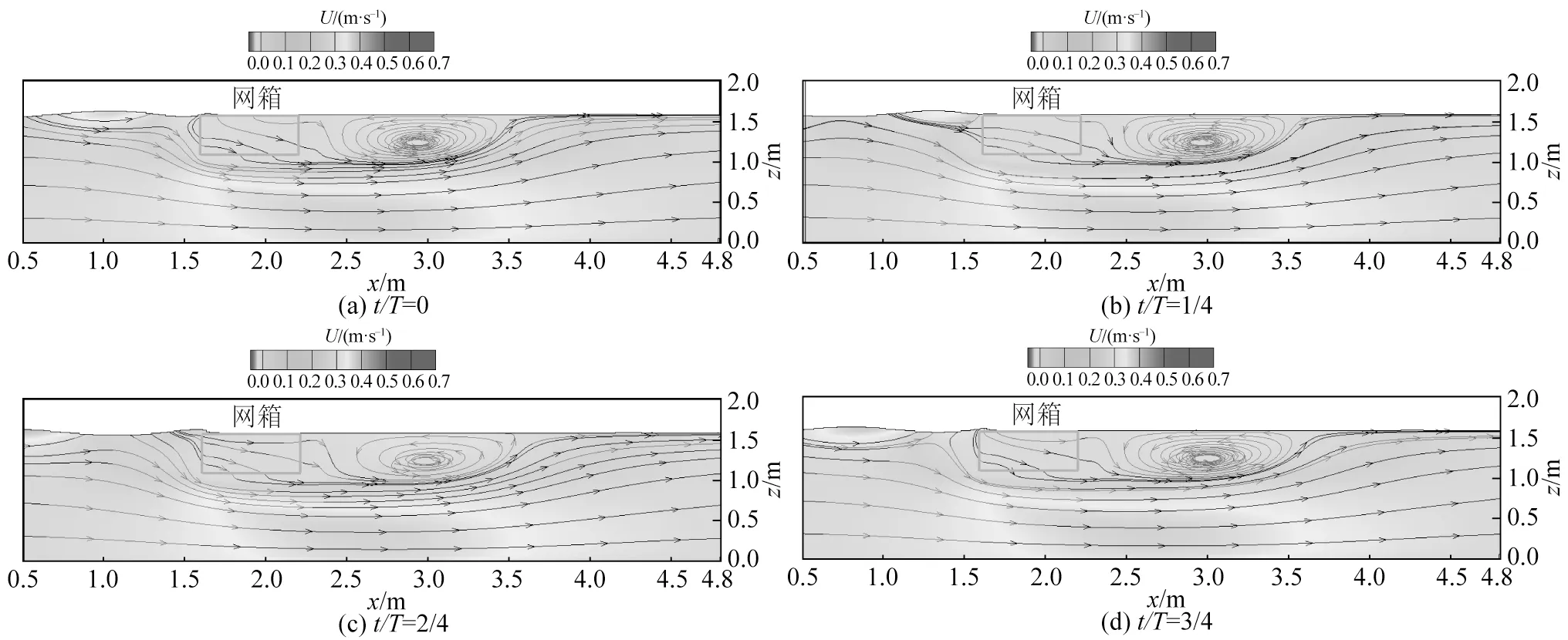
图8 工况1（操作工况）下网箱结构潜深0 m时一个周期内的流场计算结果（流线代表流动方向）Fig.8 Flow field under the operating condition of cage structure when d=0 m in one wave period (Streamlines represent the flow direction)

从图8 中可以看出：波浪、流与网箱结构相互作用过程中网箱结构起到了一定的阻流效应，网箱结构内部流体速度得到了一定的消减；网箱结构背流侧有一定的涡旋形成，速度有一定的减小；网箱结构下方流体速度有一定的增加，这一现象可能是波流作用下网箱结构的阻流作用导致的，并且这一现象在Bi 等［41］物理模型试验结果中也存在，在流的作用下网箱结构下方流体流速呈现增加的现象。

图9给出了1a#～1c#、2a#～2c#、3a#～3c#这9个测点的速度变化曲线。

图9 工况1（操作工况）下网箱结构潜深0 m时的各测点速度历时曲线Fig.9 Velocity variation curve of the measuring points under operating condition when d=0 m

从图9 中可以看出：从测点编号1、2、3 来看，随着测点位置靠后流速逐渐减小，从a、b、c 来看，随着淹没深度的增大，流速也减小；网箱结构内部流场水面附近的速度要大于网箱结构内中下部的流场速度，网箱结构内底部及网箱结构内后半部分流场的速度最小。

5.2 工况2下的流场特性计算结果与分析

工况2（极端工况）下网箱结构顶部淹没深度从0 m开始进行模拟计算，依次模拟网箱结构顶部淹没深度d为0.0、0.2、0.4、0.6、0.8 m，通过对比各种情况下的流场及监测点速度变化，确定网箱结构的最佳淹没深度范围。图10给出了工况2（极端工况）水深D为1.6 m，波浪周期T=2.1 s，波高H=0.36 m，沿深度方向平均流速0.364 m/s，网箱结构顶部潜深0.0、0.2、0.4、0.6、0.8 m 时波浪与网箱结构作用10个波浪周期后（10.25倍周期）的流场，从图10中可以看出：波流作用下网箱结构对流体速度具有一定的阻尼作用，网箱结构内部流场得到了一定的消减，由于网箱结构阻尼作用，网箱结构下方流体速度会有稍许增大。

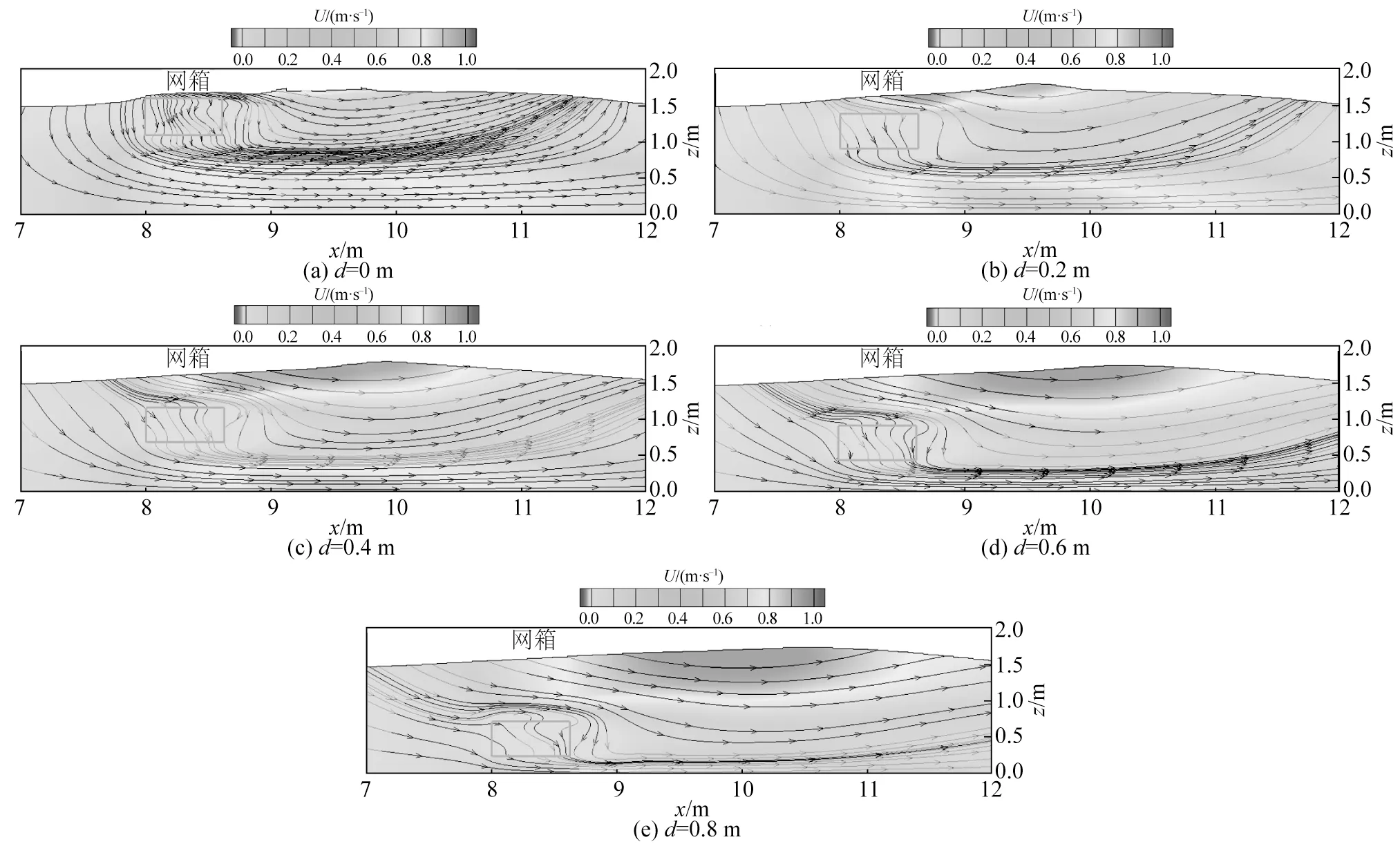
图10 工况2（极端工况）下10.25倍周期时的流场计算结果（流线代表流动方向）Fig.10 Flow field under extreme operating condition of the cage structure when t=10.25T (Streamlines represent the flow direction)

图11 给出了波流作用下网箱结构顶部淹没深度d为0.0、0.2、0.4、0.6、0.8 m 时网箱结构内部1a#～1c#、2a#～2c#、3a#～3c#这9 个测点的速度变化曲线。从图11 中可以看出：淹没深度d= 0 m 时网箱结构内部各测点的速度及速度波动最大，且在网箱结构内垂向中部位置速度最大，网箱结构内前半部分的速度变化幅度最大，网箱结构内后半部分速度较为稳定；淹没深度d=0.8 m 时网箱结构内部各测点的速度及速度波动最小，网箱结构内前半部分和后半部分流场速度变化较小；通过不同淹没工况网箱结构内部各测点速度的时间历程变化可知，网箱结构顶部淹没深度为0.4、0.6、0.8 m 这3 种工况下的各测点速度历时变化曲线最为接近，网箱结构内部流场分布较为一致。

图11 工况2（极端工况）下网箱结构d=0.0, 0.2, 0.4, 0.6, 0.8 m时的各测点速度历时曲线Fig.11 Velocity variation curve of the measuring points under extreme operating condition when d=0.0, 0.2, 0.4, 0.6, 0.8 m

深海养殖网箱结构正常工作状况下，网箱结构应布置在水面附近。极端工况下，为了保障网箱结构的安全及维护鱼类生活的最佳生境，应使得网箱结构下潜到一定深度来保证获得并维持与操作工况时尽可能相同的网箱结构内部流场特性，但网箱结构的下潜深度也要考虑触底问题和经济问题。由以上计算结果可知：工况2下（极端工况）网箱结构顶部淹没深度从0.0 m到0.8 m的过程中，网箱结构内部流场的变化是依次更为稳定的，且网箱结构顶部淹没深度为0.4、0.6、0.8 m这3种工况下测点速度的历时变化曲线最为接近，说明网箱结构淹没深度d在0.4～0.8 m 范围内时淹没深度的变化对网箱结构内部流场的影响最小，网箱结构内部的整个流场相对稳定，此时的网箱结构淹没深度为最佳淹没深度。

6 结 语

基于OpenFOAM 平台开发了海上风电钢管桩基础上升降式网箱在波流共同作用下的水动力数值研究模型，采用多孔隙介质对网衣进行简化计算，开展了极端工况下升降式网箱的水动力特性研究，并与操作工况下的流场特性进行了对比分析，明确了极端工况下升降式网箱结构的最适宜下潜深度范围。研究成果表明：极端工况下升降式网箱结构的最佳下潜深度为水深的1/4～1/2，该下潜深度范围内网箱结构内部流场分布较为均匀，流场速度变化幅度相对稳定，为网箱结构的最佳淹没深度。该研究成果可为海上风电钢管桩基础上安装的网箱结构设计提供参考，以对升降式网箱结构极端海况下网箱结构的有效下潜深度范围进行界定，为升降式网箱结构极端海况下的安全性提供有效保障。

采用数值模拟方法研究了集成于风电钢管桩基础上的养殖网箱结构波浪场变化特性，试图从鱼类生境角度对网箱结构下潜深度给出建议。研究中网箱结构被简化为固定的多孔介质结构，忽略了网衣结构的变形对流场特性的影响，而实际上网衣在水流的强烈作用下会发生变形，涉及到运动网衣对流场特性的影响，相关内容将是未来的研究范围。