初中数学数形结合思想教学案例分析

施秋荣

摘要：数与形是数学的两大基本元素，初中数学教学与学习不能脱离数与形而独立存在.在数学教学中积极应用数形结合思想，可使某些抽象的数学问题变得更加直观、生动，进而促使抽象思维转化成形象思维，帮助学生更好把握数学问题本质.本文中从实际出发，立足实际教学内容，从有理数、不等式、函数、几何四个方面分析了初中数学数形结合思想的具体应用，意在确保数形结合思想能够得到有效落实，学生核心素养可以得到有效提升.

关键词：初中数学；教学研究；数形结合思想；案例分析

在教育深化改革背景下，教师要切实落实立德树人根本任务，深入推进初中数学课堂教学改革，落实学生主体地位，聚焦学生核心素养的培育，探索课堂教学的新范式.在此背景下，“以数解形、以形助数”的数形结合思想的价值和作用愈发凸显，得到了众多数学教师的青睐，且收获了良好的教学效果.新形势下，教师要深入探索教学内容，并立足教学内容之上，以教学目标为指引，贯彻落实数形结合思想.

1 数形结合思想概述

1.1 数形结合思想的定義

数形结合思想指的是利用“数”与“形”之间的关系对数学知识点和数学问题进行研究，并以此为数形转换找到一定条件的一种数学思维方法[1].

1.2 数形结合思想的转换方法

（1）以数解形

以数解形，即将图形转换成数.具体指的是通过分析数学题目中的各种图形，挖掘其所包含的代数知识，在明确图形和数量关系的基础上，用“数”的方式将“形”的属性表现出来，从而使复杂的图形变得简单明了，帮助学生实现快速解题[2].

（2）以形助数

以形助数，即将数转换成图形.具体指的是针对数学中难以用代数进行描述和表达的抽象知识点，可通过合理引入图形的方式将抽象难懂的数学知识点转化为比较直观的形象表达，用“形”的具体将“数”的抽象表现出来，进而帮助学生解决难以理解的数学问题.

（3）数形互变

数形互变，即数字和图形之间的相互转化.具体指的是在解决数学问题的过程中，以题意为基础进行联想，将抽象的数学语言转化成图形，将题目中的图形以数量关系的方式表达出来.这能够让抽象的数学问题变得简单、易解答［3］.

2 初中数学数形结合思想教学案例分析

2.1 数形结合思想在有理数中的应用

有理数是初中数学较为重要的内容之一，且具有较强的逻辑性.对于部分学生而言，有理数学习具有一定的难度.此时，从学生学习能力和实际水平出发，依托数形结合思想，灵活地引入“数轴”这一图形工具，可将数学问题化难为易，进而帮助学生快速、准确地解决数学问题.

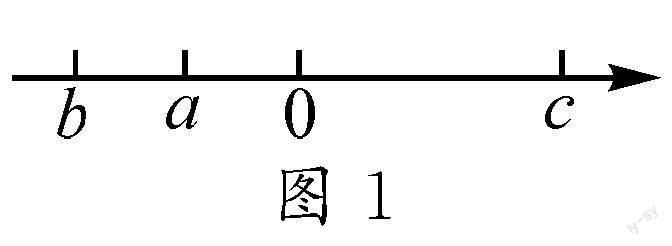
例1 已知a，b，c在数轴上的位置如图1所示，化简|a|－|a+b|+|c－a|+|b－c|.

分析：通过分析数轴可知b＜a＜0＜c，然后可根据有理数的运算法则，判断出绝对值里的代数式的正负性，最后根据绝对值的性质化简.

解析：由数轴，得b＜a＜0＜c.

所以a+b＜0，c－a＞0，b－c＜0.

故

|a|－|a+b|+|c－a|+|b－c|

=－a+a+b+c－a－b+c

=－a+2c.

点评：通过分析数轴准确判断a，b，c之间的大小关系和正负情况，既可以便于学生直观地理解正、负数的概念及其区别，还可以确保学生快速、准确地得到结果.

2.2 数形结合思想在不等式中的应用

中考数学中，代数问题往往以一元二次方程（不等式）的形式出现.在不等式的相关习题中，灵活应用数形结合思想，利用二次函数图象解决不等式问题，这样既可以降低不等式习题的难度，还可以让学生感受到学习的乐趣.更重要的是，这有助于学生数形结合能力的提升，可为学生后续快速、准确解答不等式问题奠定良好基础.

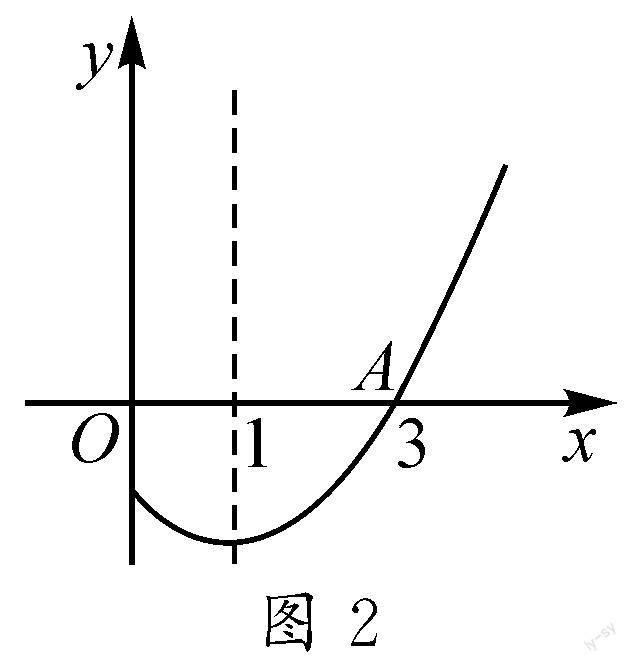
例2 如图2为二次函数y=ax2+bx+c图象的一部分，其对称轴为直线x=1，若其与x轴一交点为A（3，0），则由图象可知，不等式ax2+bx+c＜0的解集是[CD#3].

分析：根据二次函数的对称性，可得出图象与x轴的另一个交点坐标，进而结合图象可得出ax2+bx+c＜0的解集.

解析：由图象可知，二次函数图象对称轴为x=1，与x轴的一个交点坐标为（3，0），所以

图象与x轴的另一个交点坐标为（－1，0）.

结合图象可知，

不等式ax2+bx+c＜0的解集即是y<0的解集.

因此，不等式ax2+bx+c＜0的解集是－1＜x＜3.

点评：利用二次函数的图象和性质解不等式，可以有效降低解题难度，也可以减少计算量.

2.3 数形结合思想在函数中的应用

函数是初中学生新接触的内容，无论从理解，还是接受方面都比较困难，所以找对解题方法十分关键.在函数问题中应用数形结合思想，可提升解题效率，保证解题正确率.

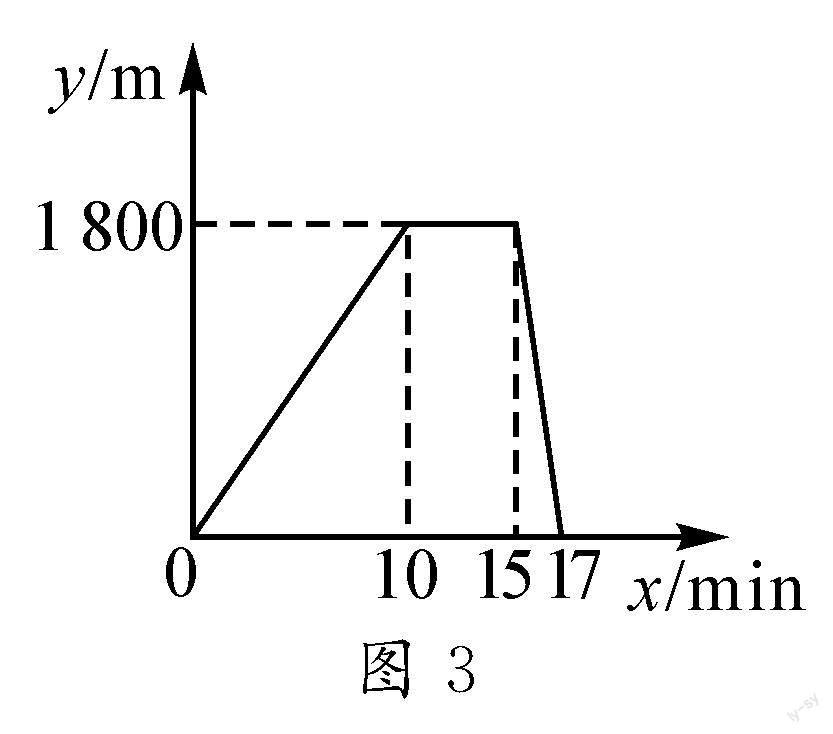
例3 周末上午，小红从家出发跑步去公园，之后在公园停留了一会，并在疲惫时选择打车回家.图3中折线表示小红离家的距离y（单位：m）和所用时间x（单位：min）之间的函数关系，则下列说法中错误的是（）.

A.小红在公园停留了5 min.

B.小红乘出租车用了17 min.

C.小红跑步的速度为180 m/min.

D.出租车的平均速度是900 m/min.

解析：为准确快速解答问题，首先要明确图中横坐标和纵坐标分别代表的实际意义——横坐标代表的是小红所用的时间，纵坐标代表的是小红离家的距离.其次，要明确该折线图由三部分构成.其中第一段表示“小红从家出发跑步去公园”，且离家的距离越来越远，到10 min时，小红距离家的距离为1 800 m，这说明小红家到公园的距离为1 800 m，且小红的跑步速度为1 800÷10=180（m/min）;第二段表示“小红在公园停留了一会”，因此该段中，只有时间在增加，而小红家离家距离并没有增加，且小红停留的时间为5 min.第三段表示“小红在打车回家”，因此，小红离家的距离越来越近，到17 min时，小红与家的距离为0 m，说明小红已经到家，且花费的时间为17-15=2（min），可以得出出租车的平均速度为1 800÷2=900（m/min）.故该题的正确答案为选项B.

点评：数形结合思想把实际问题和图象紧密地结合在了一起，不仅使学生的解题思路更加明确，缩短了学生做题时间，也提高了解题准确率.

2.4 数形结合思想在几何中的应用

初中几何知识具有抽象性特点，是学生需要掌握的重点知识和难点知识.切实强化数形结合思想在几何问题中的应用，不仅可以帮助学生以简单的方式快速解答几何问题，还可以有效培养学生的抽象思维能力.

例4 如图4所示，当菱形ABCD的面积为120 cm2时，正方形AECF的面积为50 cm2，则菱形的边长为[CD#3]cm.

分析：该题是求解长度的问题，其解题关键在于菱形和正方形都是轴对称图形，且二者都具有对角线相互垂直的性质.因此，可依托数形结合思想，用设未知数的方法，解答出正确答案.

解：设AC=2a，BD=2b，则

点评：以数解形的解题方法既可以降低习题难度，也能够为学生提供更加便捷的解题方法，有利于提高解题效率.

数形结合思想可以将形象直观的图形与抽象的数学知识进行有机结合，进而实现教学内容具体化、复杂关系简单化.因此，教师应当加强数形结合思想在数学教学中的应用，并围绕学生实际学习情况和学习特点，为学生总结出更多数形结合思想的应用思路.

参考文献：

[1]陈小红.初中数学数形结合思想教学研究与案例研究[J].读与写，2021，18（4）：157.

[2]许瑞光.基于初中数学数形结合思想教学研究与案例分析[J].文渊（中学版），2020（6）：456-457.

[3]高成荣.初中数学数形结合思想教学研究与案例分析[J].数理化解题研究，2020（29）：14-15.