建设“四性”课堂,促进有效学习
甘晓云
摘要:展开课堂有效性的探索,努力建设“四性”数学课堂,可以凸显“以生为本”的教学理念,促进学生的有效学习.文章以“完全平方公式”的教学为例,具体阐述了建设“四性”课堂,促进有效学习的方式方法.
关键词:数学课堂;完全平方公式;有效学习
当前处于知识经济迅猛发展的时代,教师肩负着培养高素质人才的使命,这就需要教师加强自身专业水平,以顺应新课程改革的时代需求[1].基于此,教师需要展开课堂有效性的探索,努力建设“四性”数学课堂,凸显“以生为本”的教学理念,积极推进课堂教学的改革.何谓“四性”课堂?该如何建设“四性”数学课堂?笔者在比较分析的基础上,基于“完全平方公式”的教学,探索阐述自身的所思所行.
1 以激趣性情境调动学习的主动性
课堂导入需做到激趣引思以调动学习的主动性,这是建设“四性”课堂的基础.这就需要教师从学科特点和学生学习水平出发,为数学问题赋予真实有趣的情境,以调动学生学习的主动性,激活学生迫切解决问题的心理需求,自主自发地投入到趣味性和挑战性的问题解决之中,最终品尝到成功的喜悦.
片段1 激情导入
故事情境:很久以前,村里住着一个贪心邪恶的地主老爷,他不仅拥有万贯家财,还拥有两块土地,一块面积是a2,另一块面积是b2.穷小子阿拉只有一块面积是(a+b)2的土地.这一天,贪心的地主老爷找到阿拉,说:“阿拉,我想用我家的两块土地和你的一块土地交换,可以吗?”如果你是阿拉,你会和地主老爷交换土地吗?
一般情况下,创设问题情境的方式多样,可以是赋予现实场景,也可以是赋予生动的情境,将其融合为情境问题.而不管采用哪种方法,我们的目的都是使其具备激趣性,让学生体验到问题的生动、鲜活、熟悉和趣味,以增强学生的情境体验,将其带入情境之中,不由自主地进行新知的探索.以上片段中,教师为数学问题添加情境,就是为问题穿上华丽的外衣,激发学生的好奇与兴趣.以兴趣驱动思维,让学生产生迫切解决问题的冲动,进而投入到问题的探索中,问题的解决和课堂氛围的高涨也就顺理成章了.
2 以针对性活动加深对数学本质的理解
增强对数学本质的理解就是指通过体验数学知识的发生过程,理解知识的来龙去脉,领悟知识间的区别与联系,完成对数学本质的洞察.这就需要教师从数学本质出发,通过针对性的设计,借助学具操作等方式,引导学生通过拼、画、剪等操作活动,切实体验数学探究的旅程,感受知识发生的过程,以形成对知识本质的深刻理解,提高思维能力和创新能力.
片段2 活动设计
活动1:想一想.
师:从片段1的故事中,你发现了哪些数学表达式?
生1:可以将(a+b)2视为(a+b)(a+b).
师:那就请你们通过两个多项式相乘这一方法进行计算.(教师快速板演学生的想法.)
师:我们称(a+b)2这一形式为“两数和的平方”,那谁能例举“两数差的平方”?(学生很快作答,教师再次板书.)
师:请同学们试着各设计1个“两数和的平方”及“两数差的平方”的式子,再借助多项式乘以多项式计算,看看结果是什么.谁愿意上来板演你的方法?(学生积极举手,教师随机请两名学生板演.)
师:我们一起来观察黑板上的式子,你能从中发现什么?
生2:我发现了三点.(1)所有结果都是三项;(2)首项与末项均是平方,前面的符号也均为正;(3)首项是前一个数的平方,末项是后一个数的平方,而中间项是两数积的2倍,同时首、末项均为正.
师:能将你的发现总结提炼一下吗?(生2思考后娓娓道来,教师完善并板演.)
生:两数和(差)的平方等于这两个数的平方和与它们积的2倍的和(差),即
(a+b)2=a2+2ab+b2,
(a-b)2=a2-2ab+b2.
活动2:拼一拼.
师:ab可对应矩形的面积,a2,b2则可对应正方形的面积.现在请同学们试着用图形去说明以上公式.可以利用边长分别为a,b(a>b)的正方形纸片各一张,长和宽为a,b的长方形纸片各一张,以小组合作的形式进行,通过想、拼、说等形式展开.(学生展开探讨,教师巡视.)
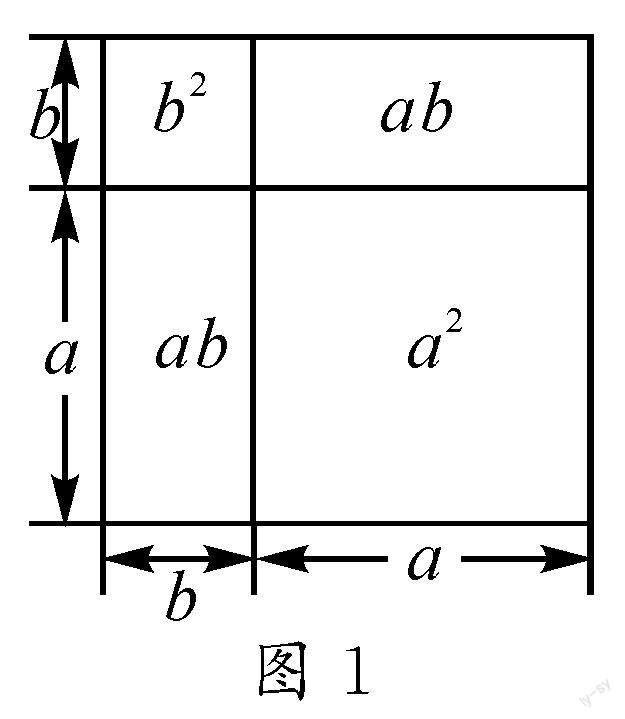
生3:如图1,我们组探索并验证了公式(a+b)2=a2+2ab+b2,利用的是整体表示和分开表示同一个大正方形的面积.
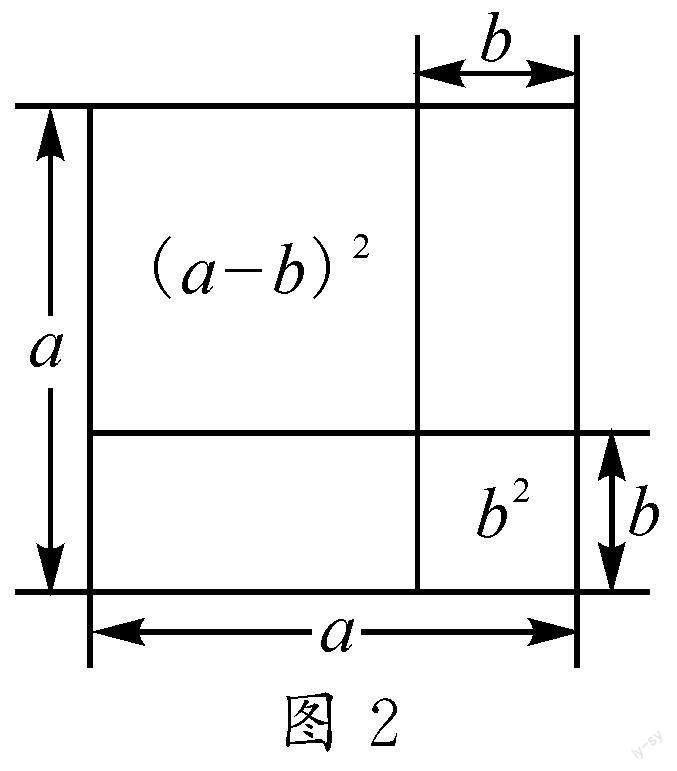
生4:如图2,我们组探索并验证了公式(a-b)2=a2-2ab+b2.左上角的小正方形边长是a-b,面积为(a-b)2,可以视为边长是a的大正方形减去2个边长和宽为a,b的长方形,由于多减了1块,因此加上1个边长为b的正方形的面积.
活动3:算一算.
问题1 图形中的a,b都是正数,那么如何说明对于任意的实数a,b,公式都成立呢?请借助多项式乘多项式的法则进行计算.
数学的美体现在“数”与“形”的协调统一,数形结合是解决问题的有效策略.以上活动设计中,教师让学生在想、拼、算中亲历知识的形成过程,感悟其中蕴含的思想和方法,感受代数和几何间的协调美,凸显对完全平方公式本质的理解和掌握[2].
3 以有效性练习加强知识的应用性
教学中最基本、最广泛的要求就是看学生课堂参与度是否高,取得的学习效果是否好.因此,在教学中,教师需要通过有效性练习让学生亲历知识应用的过程,在解决问题的过程中感悟数学概念、数学思想对现实生活的影响,切实体会到数学知识是有用的,从而自主自发地投入到新知的探索和挖掘中去,完成对知识应用性的追求.这样,数学教学才会达到应有的效果.
片段3 知识应用
师:现在大家可以替阿拉答复地主老爷了吗?
生1:当然不能换.因为(a+b)2=a2+2ab+b2,顯然比a2+b2要大.
生2:两个数进行比较也是要有前提的,这里a,b都是正数.
练习:先选择公式,再计算.
①(5+3p)2;②(2x-7y)2.
在知识应用环节回归导入环节,通过释疑解惑感受完全平方公式的应用价值.进一步地,通过练习,学生明晰公式的基本应用,了解公式间的联系,促进应用意识的建构.经历这样的学习过程,学生能透彻地理解完全平方公式的价值,实现“学以致用”.
4 以开放性问题增强学习的创新性
培养创新能力是素质教育的重心,也是新课程理念中最为关注的问题.这就需要教师针对性地设计学习活动,以开放性问题转变学习方式,为学生搭建思维的“脚手架”,更好地弥补教学中开放性不足、主体性不强、创新性不高等特征,让学生多方位、多角度去思考和探索问题,最终实现思维的进阶,增强学习的创新性.
片段4 拓展延伸
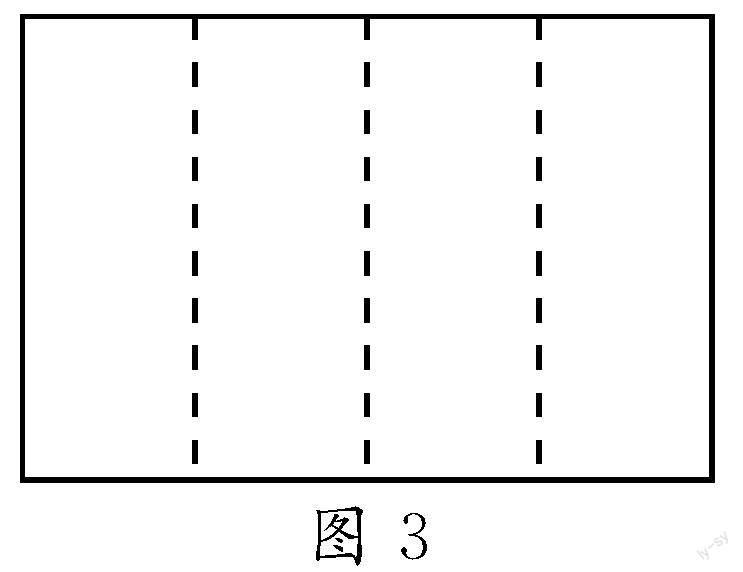
问题2 图3是一个长方形,长为4a,宽为b,用剪刀沿着虚线将其平均分为4块小长方形,再将这4块小长方形拼为图4所示的1个“回形”正方形.观察图形后,利用观察的结果解决以下问题:
(1)当m+n=5,mn=4时,m-n=[CD#3].
(2)已知(2x-500)(400-2x)=2 020,试求(4x-900)2的值.
以上片段4中教师出示的问题是教材问题的改编,改编后的问题更具开放性和挑战性,需要学生利用好本节课学习中的经验,还需要考虑等量关系的运用方式.学生在解决问题時各显神通,有的灵活应用新知,有的借助特殊值法求解,真正锻炼了学生的思维,实现了活学、活用、活化.这样的学习过程,也真正是高效而深入的.
总之,建设主动性、本质性、应用性、创新性的“四性”数学课堂,需要教师基于教学内容的内在线索精心设计教学活动,着眼于相关内容的数学本质来整体组织教学过程,让学生在激趣性情境中深入思考,在针对性活动中深度探索,在有效性练习和开放性问题中有效思维.只有这样,才能让教学达到应有的深度,才是真正有效的数学学习,才能让学生在生机勃勃的数学课堂中发展思维、提高素养.
参考文献:
[1]郭玉峰,史宁中.数学基本活动经验:提出、理解与实践[J].中国教育学刊,2012(4):42-45.
[2]厉兆云.提高学生解题能力的几点尝试[J].教学月刊(中学版),2008(4):41-43.

