初中几何问题中线段长度的求解技巧探究
卢晓雨


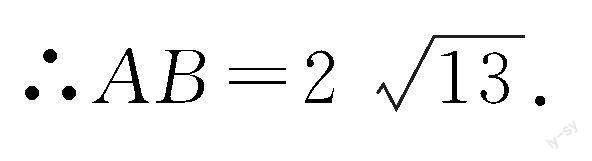
摘要:平面几何是初中数学知识中重要的一部分,线段长度的变化影响着图形的大小、形状.考查线段长度的形式多种多样,相关的问题也都十分灵活.求线段长度的基本方法有等面积法、利用勾股定理、利用相似等.本文中结合不同例题,具体分析解答求线段长度问题常见的解题思路.
关键词:平面几何;线段长度;解法思路
求线段的长度是初中几何的基础问题.解这类题目要综合考虑线段的位置关系,通过题干信息的提取,采用合适的方式进行求解.
1 利用等面积法
等面积法是指用不同方式表示同一平面图形的面积,通过面积的相互转化或面积与边、角关系的互相转化,而使问题得到解决的方法.对于三角形而言,就是指利用三角形的面积自身相等的性质,或根据等高(底)的两个三角形的面积之比等于对应底边(对应高)的比等进行解题的一种方法.利用等面积法解题具有便捷、快速的特点.解题思路大致为:①根据已知条件通过面积的相互转化或面积与边、角关系的互相转化,用不同方式表示同一三角形的面积;②通过题中已知条件进行运算即可求出所求线段长度[1].具体解题思路和步骤如以下例题所示.
例1 如图1,在Rt△ABC中,∠C=90°,AC=4,
BC=3,CD是斜边AB上的高,求CD的长度.
分析:首先根据题中已知条件,可知在一个直角三角形中∠C=90°,以及AC和BC的长度,从而可求得AB的长,又根据CD是斜边AB上的高,通过面积与边、角关系的互相转化,最后进行运算即可求出所求CD长度.
解:∵∠C=90°,
AC=4,
BC=3,
∴AB=5.
又CD为斜边AB上的高,
∴S△ABC=AC·BC
=AB·CD.
∴4×3=5CD.
例2 如图2,已知△ABC中,AD是△ABC的中线,AD=4,BC=6,AC=5,P是AB边上的一点﹐且△PBD是以BP为底的等腰三角形,求线段AP的长度.
分析:首先根据题中已知条件,可得AD⊥BC.再根据面积相等可得DH长度.同理,可得BH长度.最后根据等腰三角形的“三线合一”性质,得到PH=HB,求出PB长度,从而求出线段AP长度.
解:过D作DH⊥AB,垂足为H.
∵AC2=AD2+CD2,
∴∠ADC=90°.
∴AD⊥BC.
在△ABD中,根据面积相等可得
在Rt△BDH中,求得
根据等腰三角形的“三线合一”性质,得
PH=HB,AB=AC=5.
2 利用勾股定理
已知直角三角形的两直角边长分别为a,b,斜边长为c,则a2+b2=c2.因此,在直角三角形中,已知任意两边长,可求第三边长.构造出直角三角形,用勾股定理建立方程求线段长度的解题思路大致为:①根据已知条件构造直角三角形;②利用勾股定理建立方程;③通过计算求出所求线段长度[2].具体解題思路和步骤如以下例题所示.
例3 如图3,在Rt△ABC中,∠C=90°,AC=4,
BC=3,CD是斜边AB上的高,求CD的长度.
分析:首先根据题中已知条件,可知在一个直角三角形中,∠C=90°,以及AC和BC的长度,从而可求得AB的长.再设BD=x,表示出AD.又因为CD是斜边AB上的高,最后利用勾股定理建立方程,通过计算即可求出所求线段CD的长度.
解:∵∠C=90°,
AC=4,
BC=3,
∴AB=5.
设BD=x,
则AD=5-x.
∵CD为斜边AB上的高,
∴在Rt△ADC与Rt△BDC中,有
CD2=AC2-AD2
=BC2-BD2.
∴42-(5-x)2=32-x2.
分析:首先根据题中已知条件,设CE=x,CD=y,再表示出AC和BC,最后利用勾股定理建立方程,通过计算即可求出所求线段AB的长度.
解:设CE=x,CD=y,
∴AC=2x,BC=2y.
∴在Rt△ACD与Rt△BCE中,有
(2x)2+y2=25,
(2y)2+x2=40.
∴x2+y2=13.
∴AB2=AC2+BC2
=4x2+4y2=52.
3 利用相似
利用相似求线段长度是根据边角关系发现相似三角形的模型,从而通过运算得到所求线段长度.解题思路大致为:①根据已知条件构造出相似三角形;②设相应线段为x,建立方程;③通过计算即可求出所求线段长度.具体解题思路和步骤如以下例题所示.
例5 如图5,Rt△ABC中,∠ABC=90°,AB=3,BC=4,Rt△MPN中,∠MPN=90°,点P在AC上,PM交AB于点E,PN交BC于点F,当PE=2PF时,求线段AP的长度.
解:如图6,作PQ⊥AB于点Q,PR⊥BC于点R,则
∠PQB=∠QBR=∠BRP=90°.
∴四边形PQBR是矩形.
∴∠QPR=90°=∠MPN.
∴∠QPE=∠RPF.
∴△QPE∽△RPF.
∴PQ=2PR=2BQ.
∵PQ∥BC,
∴AQ∶QP∶AP=AB∶BC∶AC
=3∶4∶5.
设PQ=4x,
则AQ=3x,AP=5x,BQ=2x.
∴2x+3x=3.
∴AP=5x=3.
根据上述不同的求线段长度例题的分析,可以得到求线段长度的基本方法有等面积法、利用勾股定理以及利用相似等.针对不同类型问题,采取相应的解题方法进行解答.在解题过程中,应加强对问题条件的分析应用,借助已知条件和相关性质去灵活解答,以此提高解题效率.同时,也希望同学们谨记各方法的注意事项,记住各方法的适用条件,在考试中灵活加以运用,避免出现错误.
参考文献:
[1]程长宾.求线段长度最值的常用方法[J].初中数学教与学,2012(23):24-26.
[2]李丹.连结两中点所得线段长度问题的求解策略[J].初中数学教与学,2017(17):23-25.

