弹药斜装条件下包装箱参数优化设计研究

蒋磊，张俊坤，丁志雨

弹药斜装条件下包装箱参数优化设计研究

蒋磊1，张俊坤2，丁志雨1

（1.陆军装甲兵学院士官学校，长春 130117；2.32181部队，西安 710000）

为了优化弹药包装尺寸设计，提高超长弹药包装装载和运输的效率。以铁路运输过程中超长弹药包装的斜装运输为研究对象，分析弹药包装箱和车厢几何尺寸之间的数学关系，以构建斜装运输时车厢允许的弹药包装的最大长度、最小长度、最大宽度随斜装角变化的数学模型。基于该模型，可以对包装箱参数进行优化，以实现铁路车厢最大装载量。并以某型车厢为例，利用MATLAB对该数学模型进行分析计算。得到了给定车厢尺寸条件下，弹药包装相关参数随斜装角的变化规律。利用建立的数学模型可确定适合铁路车厢斜装的弹药包装的尺寸系列，为弹药包装的优化设计和高效装载运输提供了理论依据。

弹药；运输；斜装；包装设计

现代战争中，弹药承担着毁伤敌装备等的重要使命，是部队战斗力的重要载体。弹药补给与运输是合成部队装备保障的重要内容。由于弹药消耗量大，危险系数高，保障任务重[1]，使得弹药装载业务复杂、繁琐而紧迫，是战时保障供应的重点和难点[2-6]。而铁路运输具有运量大、速度快、能耗低、运行距离远等特点，最适合长途运输，是军用装备物资运输的重要途径，因此，铁路运输方式就成为远距离大批量弹药运输的首选方式[7]。弹药包装作为弹药装备储运、管理、供应的载体形式，直接影响到弹药的安全性和可靠性，甚至影响弹药作战效能的发挥[8-10]。斜装作为一种装载方式，常用于超长包装弹药的铁路运输，而与车厢尺寸不匹配的包装设计，易造成斜装装载中的空间浪费，影响装载效率。因此，有必要从基本几何关系和装载要求出发，系统深入地对弹药斜装装载问题进行分析，并研究装载规律，为弹药运输装载计划的制定和弹药包装尺寸的系列化设计提供理论依据[11]，以防止铁路运力浪费，提高弹药补给效率[12]。

1 弹药装载原则与斜装模型的构建

影响弹药运输的因素很多，如弹药的包装、需求量、储备布局、装载方式等，其中包装和装载方式不仅关系到运输工具的运力，同时关系到运输过程的安全，必须予以重视。

1.1 弹药装载原则

弹药装载是弹药补给中的重要环节，各类弹药的装载量是制定弹药运输计划、实施车辆调度的重要依据。由于弹药的危险性，确定了弹药的装载必须遵守以下原则[7,13-14]：

1）总质量不能超过车辆的载质量。

2）弹药的装载高度不超过规定高度。

3）弹药装载应均衡平稳。

4）对于火箭弹和已安放引信的弹药，弹药不得与车辆行驶方向相同，并将弹药固定牢固，因此超长弹药只能斜装，具体装载方式如图1所示。

1.2 斜装模型构建

由于弹药包装箱的长度超出了运输车辆车厢的宽度，造成弹药无法横装运输，必须采用斜装运输。此时由于车辆车厢几何尺寸的限制，使得斜装条件下弹药包装箱的长宽尺寸与斜装角需满足一定的数学关系。

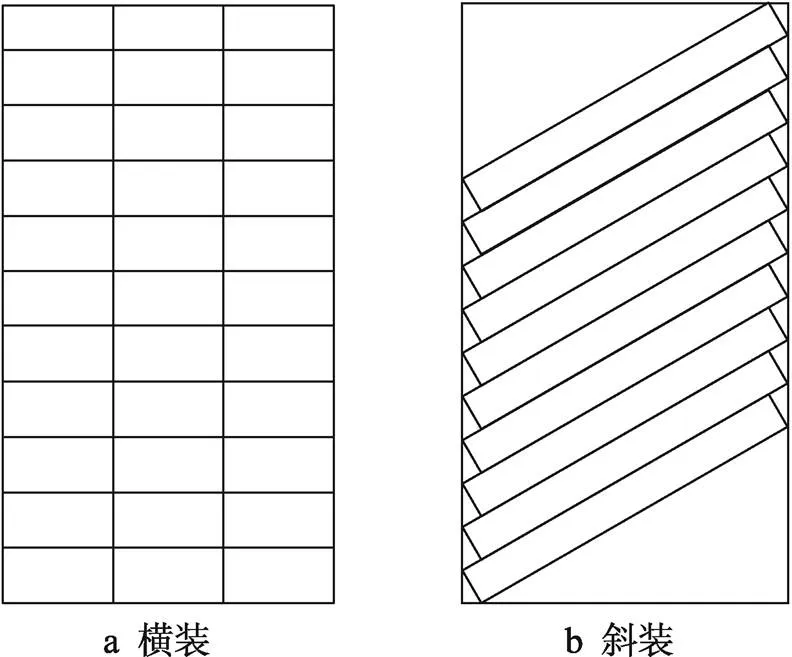
图1 弹药装载方式

车辆车厢尺寸如图2所示，弹药包装箱在车厢中的斜装方式如图3所示。其中阴影部分为弹药包装箱，1、2、3为车厢的长、宽和车门的宽，、为包装箱的长和宽，为弹药包装箱的斜装角。

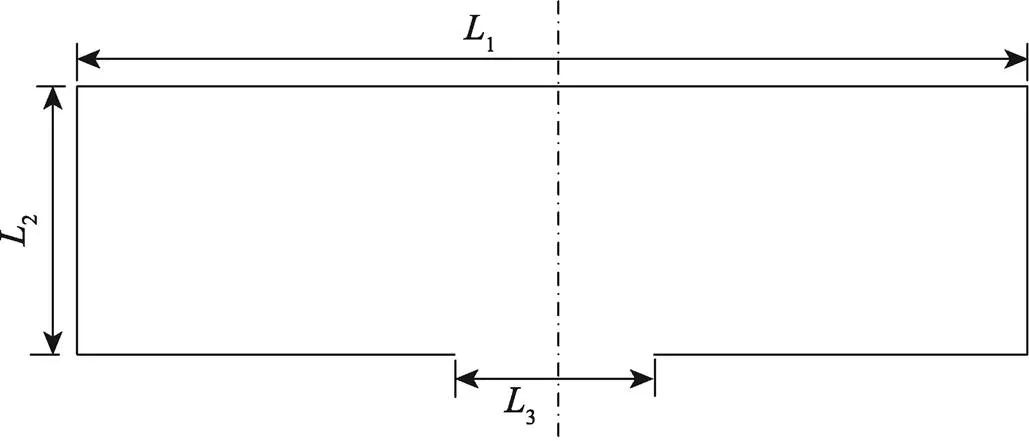
图2 车厢的几何尺寸

通过图中弹药包装箱几何尺寸随斜装角的变化关系，可得斜装角的最小值min满足以下方程：

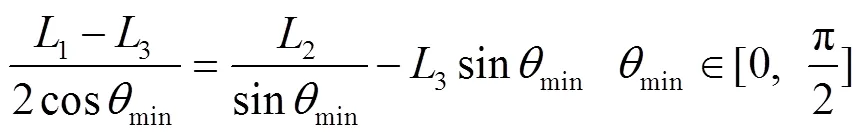
随着斜装角的变化，车厢允许的条件下斜装的弹药包装箱的长度和宽度也在不断变化，通过数学分析可构建斜装条件下，弹药包装箱的长度最大值与最小值，以及弹药包装箱宽度最大值随斜装角的变化规律，如式（2）～（4）所示。

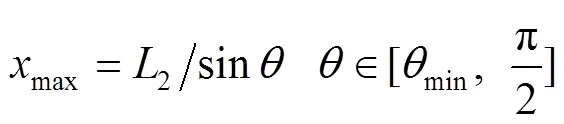
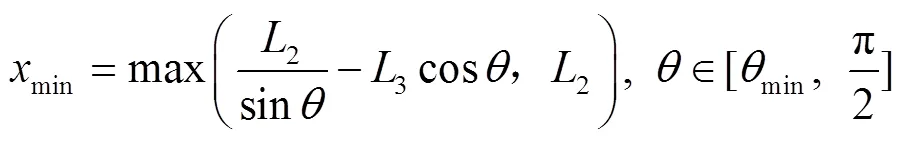
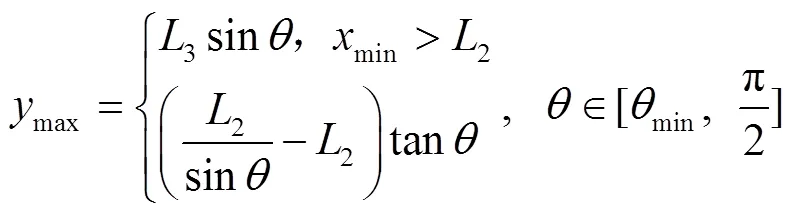
为进一步研究斜装条件下，包装箱长度、宽度和斜装角之间的变化关系，可绘制如图4所示的几何关系。

通过图4中的几何关系，可得包装箱长度随包装箱宽度和斜装角变化的规律，见式（5）～（6）。

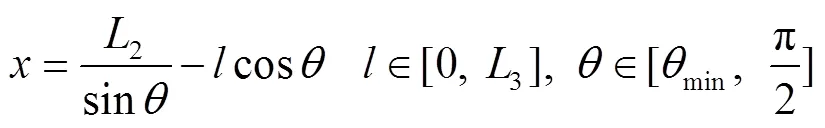
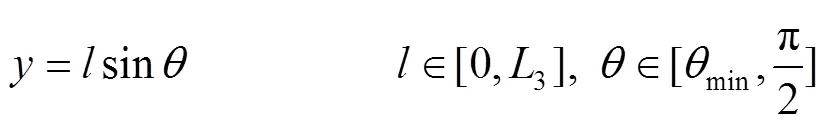
式中：为斜装条件下，弹药包装箱长度在车厢长度上的投影。

­

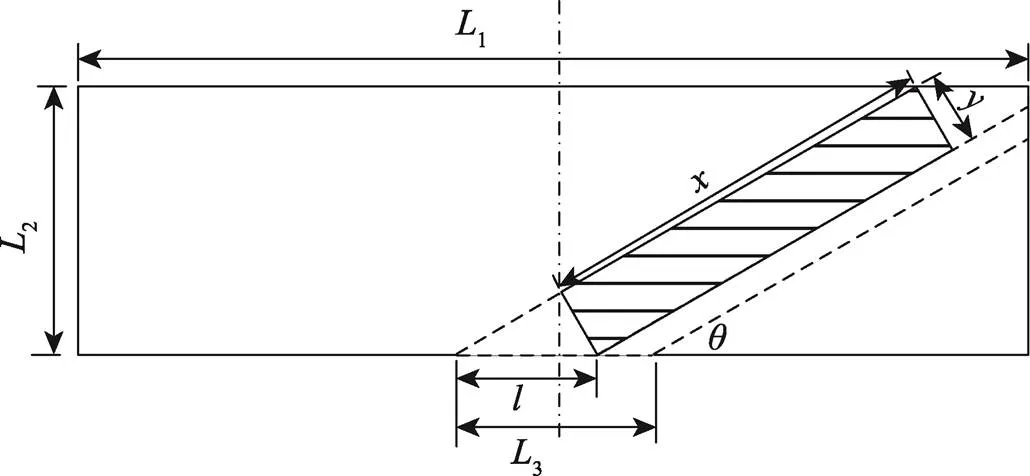
联立式（5）、式（6）可得：

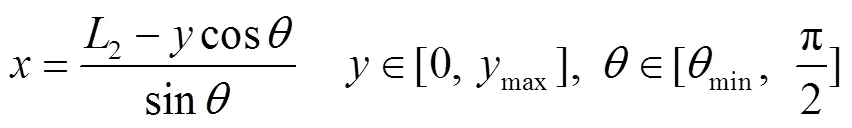
其中max可通过联立式（1）、式（3）和式（4）求得。

通过以上分析，得出了车厢斜装弹药包装箱时，弹药包装箱长度、宽度与斜装角之间的关系，见式（7），从而为指导弹药装载、制定运输计划提供了理论依据。

为使斜装条件下装载数量达到最大化，必须使得包装箱宽度沿包装箱长度方向车厢长度方向上的投影为(1–3)/2的约数，且包装箱宽度在车厢长度方向上的投影小于3。

即：

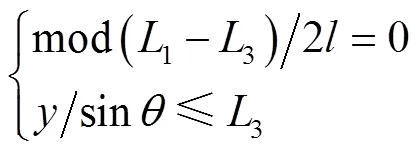
其中，mod为Matlab中的求余函数，因此在斜装运输下，包装箱的最优宽度是离散的。

综上所述，在斜装条件下包装箱的最佳参数见式（9）。

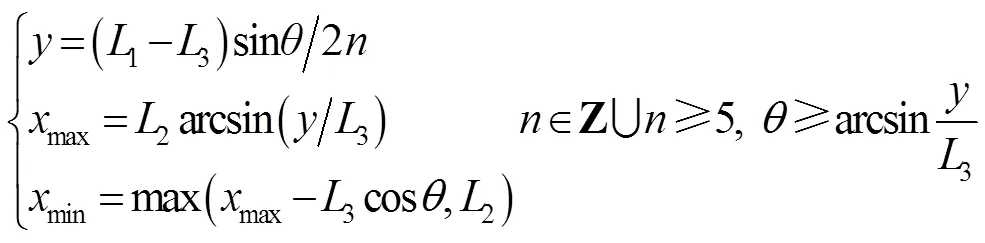
2 模型的应用与分析

目前用于弹药铁路运输的火车车厢型号不同，尺寸也各不相同。本文以某型车厢为例，对所建模型进行了分析和计算，该型车厢的几何尺寸为1=16 094 mm、2=2 800 mm、3=2 539 mm。

将车厢的几何尺寸代入式（1）～（4），利用MATLAB可绘制如图5所示的弹药包装箱最大长度、最小长度和最大宽度随斜装角的变化曲线。

从图5中可以直观地看出，随着斜装角的不断增加，包装箱的最大长度在逐渐减小，且减小的趋势逐渐变缓，最终趋近于2 800 mm。这是因为斜装的前提条件是包装箱的长度大于车厢的宽度。随着斜装角的不断增加，包装箱的最小长度先增加，在斜装角约为21.88°（解析解为22.45°）时发生转折，这是包装箱由斜装方式2向斜装方式1过渡时造成的。随着斜装角度的继续增加，包装箱的最小长度逐渐减小，且减小的速度越来越慢，在斜装角约为35.06°时，包装箱最小长度的变化曲线在此发生转折，且此后的最小长度的临界值一直为2 800 mm。这是因为斜装的必要条件为包装箱的长度必须大于车厢的宽度。随着斜装角的不断增加，包装箱的最大宽度逐渐增加，在斜装角约为35.06°时曲线发生转折，开始逐渐减小。这是由于当斜装角小于35.06°时，包装箱的最大宽度由车门宽度和斜装角决定；而当斜装角大于35.06°时，包装箱的最大宽度由包装箱的最大长度和斜装角决定。

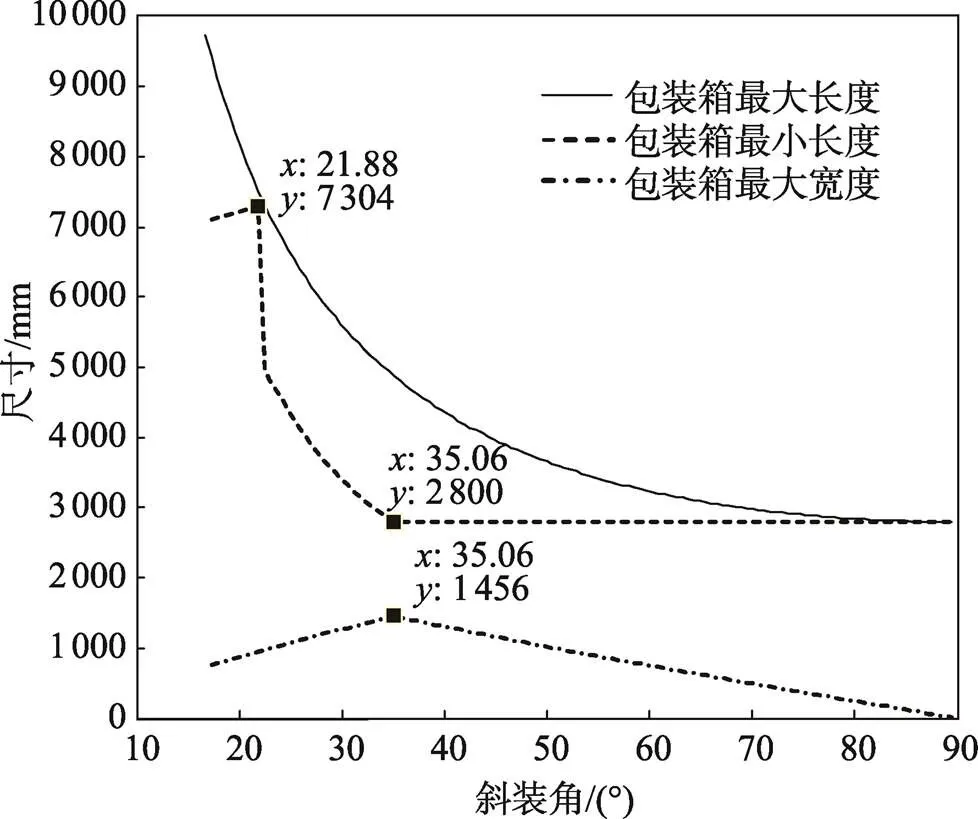
图5 弹药包装箱的最大长度、最小长度和最大宽度随斜装角的变化曲线

将车厢的几何尺寸代入式（7）进行计算，并利用MATLAB绘制弹药包装箱长度随包装箱宽度和斜装角的变化曲面，如图6所示。

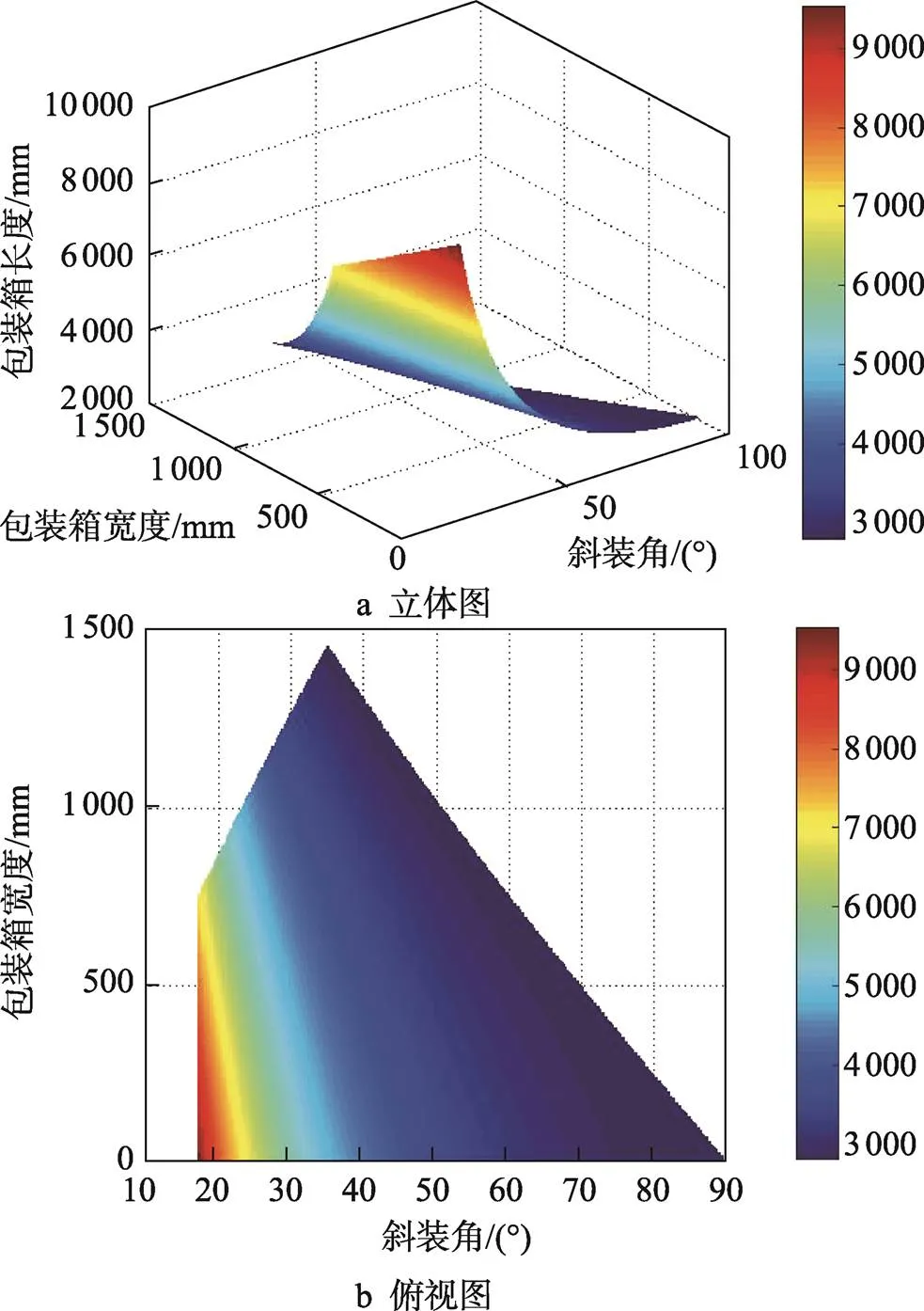
图6 包装箱长度随包装箱宽度和斜装角的变化规律

从图6可以看出，斜装角一定时，随着包装箱宽度的增加，包装箱的长度在逐渐减小；包装箱宽度一定时，随着斜装角的增加，包装箱的长度也在逐渐减小，进而可以得出在一定包装箱宽度下，车厢所能允许的包装箱最大长度；当包装箱的长度一定时，则斜装角与包装箱的宽度成反比。另外从图6中包装箱长度的变化规律可知，随着包装箱宽度和斜装角的增加，二者对包装箱长度变化的影响越来越小。

综合图5和图6可以得出，对于算例中的车厢，可达到最佳装载条件的部分包装箱参数见表1。

表1 算例包装参数

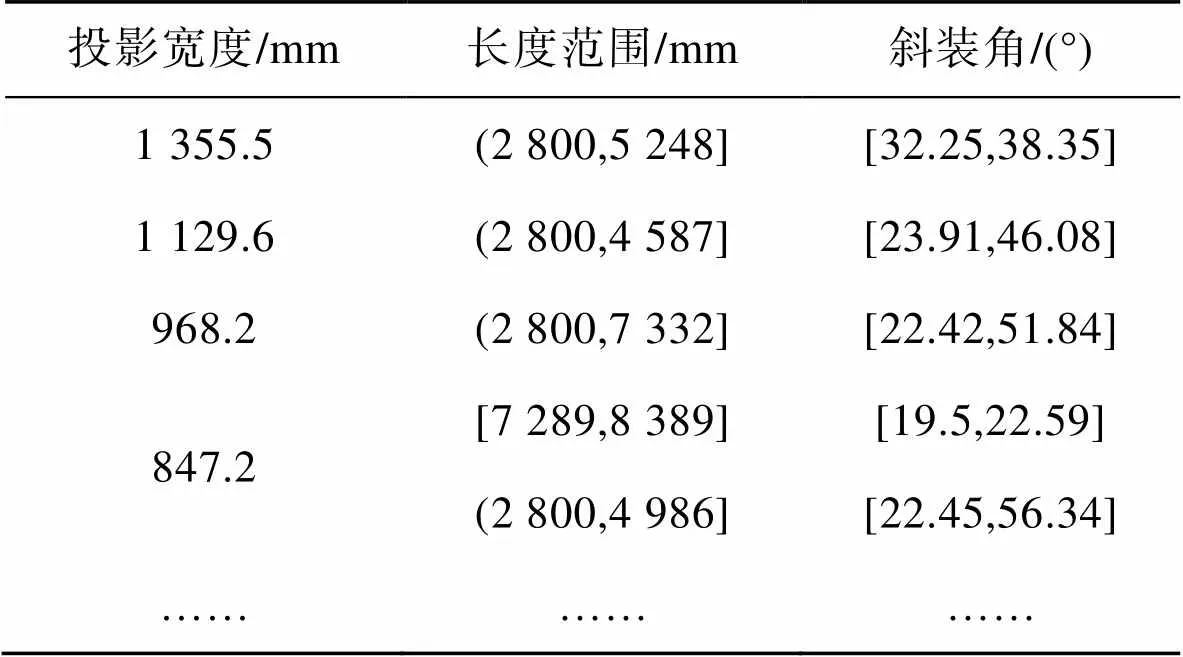
Tab.1 Some optimal parameters of packaging container

通过上面的计算和分析，可以得出算例中的车厢在斜装弹药时，对弹药包装长宽的要求，以及在最佳装载条件下包装箱的参数，从而为包装箱的设计提供了理论依据，以指导弹药的装载形式和提高运输效率。

对于常见的铁路棚车车厢尺寸，在上述计算方法和现行包装标准[15]的基础上，根据给定的常见包装长度，可计算出符合最佳斜装装载条件的部分包装尺寸参数，如表2所示。

表2 常见铁路棚车适用的斜装弹药包装参数

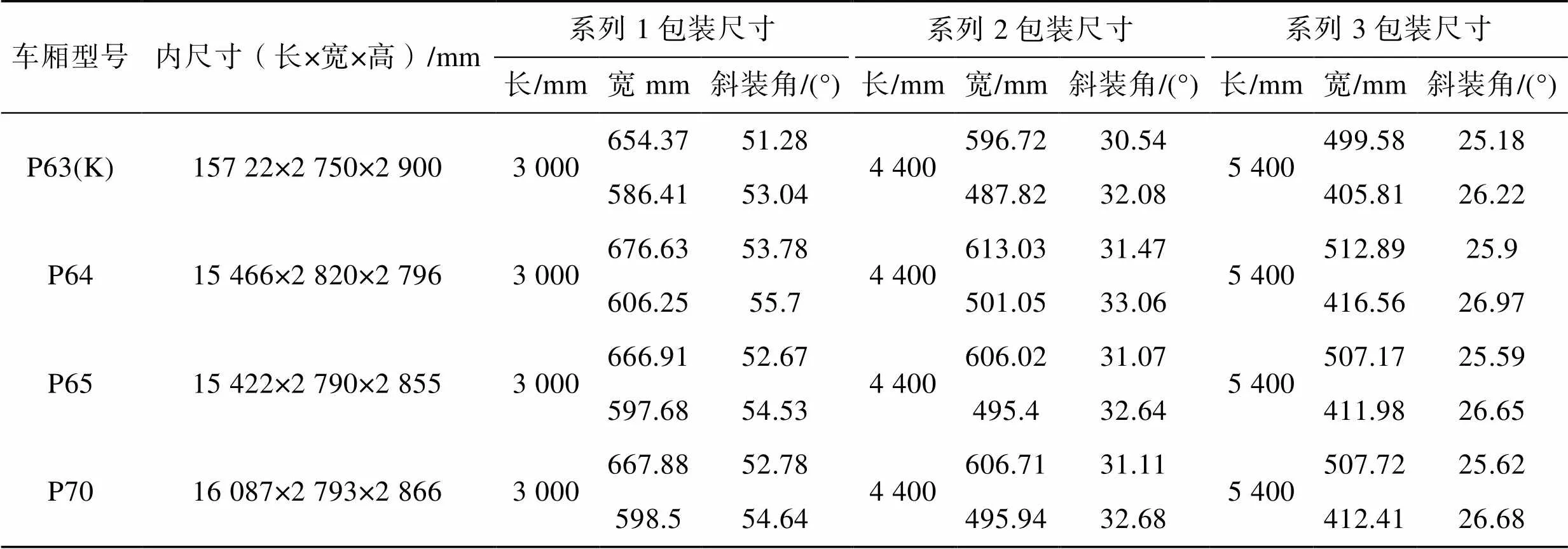
Tab.2 Ammunition packing parameters for skewed installation in common railway box car

3 结语

斜装运输作为一种超长军用危险品的运输方式，对提高其装载和运输效率进行研究有一定的必要性。弹药斜装时，包装箱和车厢几何尺寸之间具有一定的数学关系，由此可以构建出斜装运输时车厢允许弹药包装的最大长度、最小长度、最大宽度与斜装角之间的数学模型，以及弹药包装长度、宽度和斜装角之间的数学模型，同时在分析最佳装载条件的基础上，建立出包装箱参数优化模型。结合具体的车厢尺寸，利用MATLAB对各数学模型进行分析计算，能够得到各模型的变化规律，据此能够简单清楚地判断一种弹药包装箱是否可用某型车厢进行斜装运输，并得出为满足该型车厢最大装载效率的包装箱最佳参数，将该参数用于包装尺寸的优化设计，有助于提高弹药的装载和运输效率。

[1] 关继成, 李良春. 信息化条件下弹药保障需求分析[J]. 兵工自动化, 2017, 36(8): 47-50.

GUAN Ji-cheng, LI Liang-chun. Demand Analysis of Ammunition Support under Information Condition[J]. Ordnance Industry Automation, 2017, 36(8): 47-50.

[2] 帅元, 徐辉, 孙奇龙. 陆军合成部队战时弹药供应保障效能评估分析[J]. 装甲兵学报, 2022, 1(5): 70-73.

SHUAI Yuan, XU Hui, SUN Qi-long. Effectiveness Evaluation and Analysis of Ammunition Supply Support for Army Combined Forces in Wartime[J]. Journal of Armored Forces, 2022, 1(5): 70-73.

[3] 宋豪文, 贾红丽, 王亚彬等. 通用弹药铁路运输风险影响因素分析[J]. 军事交通学报, 2022, 1(12): 6-12.

SONG Hao-wen, JIA Hong-li, WANG Ya-bin. Analysis on Risk factors of Railway Transportation of General Ammunition[J]. Journal of Military Transportation, 2022, 1(12): 6-12.

[4] 陈军文, 崔利海. 基于弹药能力发展的包装需求与对策分析[J]. 包装工程, 2009, 30(10): 62-63.

CHEN Jun-wen, CUI Li-hai. Analysis of Packaging Demand and Countermeasures Based on Ammunition Capacity Development[J]. Packaging Engineering, 2009, 30(10): 62-63.

[5] 占超, 何显鹏, 侯素娟. 美军弹药信息化保障给我军的启示[J]. 价值工程, 2020, 39(12): 189-190.

ZHAN Chao, HE Xian-peng, HOU Su-juan. Enlightenment of U.S. Army Ammunition Information Support to PLA Ammunition Support[J]. Value Engineering, 2020, 39(12): 189-190.

[6] 蒋丽华, 王帅, 余化龙. 美军弹药配送保障模式研究与启示[J]. 军事交通学报, 2023, 2(1): 79-83.

JIANG Li-hua, WANG Shuai, YU Hua-long. Research and Enlightenment of Ammunition Distribution Support Mode of US Army[J]. Journal of Military Transportation, 2023, 2(1): 79-83.

[7] 鲍平鑫. 铁路军事运输[M]. 北京: 解放军出版社, 2007.

BAO Ping-xin. Railway Military Transportation[M]. Beijing: Chinese People’s Liberation Army Press, 2007.

[8] 徐露梅. 战斗部抗爆能力及隔爆技术研究[D]. 沈阳: 沈阳理工大学, 2022: 1-6.

XU Lu-mei. Study on Anti-Explosion Capability and Anti-Explosion Technology of Warhead[D]. Shenyang: Shenyang Ligong University, 2022: 1-6.

[9] 张凯. 探讨弹药包装现状及发展趋势[J]. 中国设备工程, 2022(20): 233-235.

ZHANG Kai. Discussion on the Present Situation and Development Trend of Ammunition Packaging[J]. China Plant Engineering, 2022(20): 233-235.

[10] 杨永伟, 张静, 王清晨. 弹药包装箱铁路运输试验问题及对策[J]. 包装工程, 2019, 40(7): 246-249.

YANG Yong-wei, ZHANG Jing, WANG Qing-chen. Problems and Countermeasures of Railway Transport Test for Ammunition Packing Boxes[J]. Packaging Engineering, 2019, 40(7): 246-249.

[11] 辛昕, 余贻荣, 杨永伟. 弹药铁路运输包装试验刍探[J]. 军事交通学院学报, 2012, 14(7): 57-60.

XIN Xin, YU Yi-rong, YANG Yong-wei. Railway Transportation Test on Ammunition Pack[J]. Journal of Military Transportation University, 2012, 14(7): 57-60.

[12] 宣兆龙, 易建政, 段志强. 基于弹药安全性的运输装载决策系统研究[J]. 军械工程学院学报, 2006, 18(3): 34-36.

XUAN Zhao-long, YI Jian-zheng, DUAN Zhi-qiang. Research on Loading Decision-Making System Based on the Security of Ammunition[J]. Journal of Ordnance Engineering College, 2006, 18(3): 34-36.

[13] 李德鹏, 戴祥军. 弹药储运安全[M]. 石家庄: 军械工程学院, 2004: 223-235.

LI De-peng, DAI Xiang-jun. Ammunition Storage and Transportation in Safety[M]. Shijiazhuang: Ordnance Engineering College, 2004: 223-235.

[14] 杨永伟, 张瑞鹏, 吴东广. 弹药铁路棚车运输装载加固方案[J]. 军事交通学院学报, 2016, 18(3): 19-22.

YANG Yong-wei, ZHANG Rui-peng, WU Dong-guang. Loading Reinforcement Scheme for Ammunition Railway Transportation with Boxcar[J]. Journal of Academy of Military Transportation, 2016, 18(3): 19-22.

[15] GJB 1444A—2019, 弹药包装通用规范[S].

GJB 1444A-2019, General Specification for Ammunition Packaging[S].

Optimal Design of Parameters for Packaging Container under Ammunition Skewed Installation

JIANG Lei1, ZHANG Jun-kun2, DING Zhi-yu1

(1. NCO School, Army Academy of Armored Forces, Changchun 130117, China; 2. 32181 Unit of PLA, Xi'an 710000, China)

The work aims to optimize the design of ammunition packaging size, so as to improve the efficiency of loading and transportation of ultra-long ammunition packaging. With the skewed transportation of ultra-long ammunition packaging by railway as the research object, the mathematical relationship between the geometric size of ammunition packaging container and carriage was analyzed, so as to construct a mathematical model of the maximum length, minimum length and maximum width of ammunition packaging allowed by carriage changing with the skewed angle during skewed transportation. Based on this model, the parameters of packaging container were optimized to realize the maximum loading capacity of railway carriage. With a certain carriage as the example, MATLAB was used to analyze the established model. The change law of ammunition packaging parameters with skewed installation angle under the condition of a given carriage size was obtained. The established mathematical model can be used to determine the size series of ammunition packaging suitable for skewed transportation by railway carriage, which provides a theoretical basis for the optimal design of ammunition packaging and efficient loading and transportation.

ammunition; transportation; skewed installation; packaging design

TB482.2

A

1001-3563(2023)23-0302-05

10.19554/j.cnki.1001-3563.2023.23.036

2023-04-20

装备综合研究项目（LJ2022C030145）

责任编辑：曾钰婵