基于应力—强度模型某包装箱结构强度分析
王 伟,常新龙,张有宏
(火箭军工程大学导弹工程学院,陕西 西安710000)
0 引言
在运输过程中,产品的安全很大程度上依赖于包装箱的力学性能[1]。当包装箱承受载荷超过材料的强度极限时,就会发生故障。包装箱的强度必须满足压力要求,变形必须处于可控范围之内[2]。李海连等[3]利用有限元软件对包装箱进行强度分析,并对其气密性进行实验分析;敖文刚等[4]将有限元软件与力学知识结合,对包装箱进行定性与定量分析;Frank等[5]对板材包装结构进行了强度分析。
本文针对产品运输、吊装等过程,对包装箱进行受力分析,并利用应用有限元方法进行了强度校核。首先建立了简化产品包装箱的有限元模型,并对其在不同工况下进行受力分析,以此计算为依据,校核了包装箱强度是否满足使用需要。
1 物理模型及计算参数
某型产品包装箱是由铝板、云母板、铝蜂窝板、导轨以及铝型材框架焊接而成的框架结构,箱内承受正压力,包装箱表面有六处吊装孔位材料。产品包装箱的尺寸为990 mm*990 mm*5 710 mm,包装箱外部为2 mm厚铝板,内侧采用铝合金框架结构,全部焊接,并使用硬质石英板包裹其内侧结构。
包装箱在运输及吊装过程主要涉及三种工况:
(1)产品与其包装箱起吊并运送至运输车运输时,包装箱承受载荷4.4 t,在起吊瞬间受到重力加速度2g,需要分析包装箱吊装孔位结构的强度分析;
(2)两个包装箱体共同运输时,箱体内装置产品,包装箱叠加,承受载荷重力,需要分析叠加在上部的包装箱底以及叠加在下的包装箱顶、侧壁的强度分析,叠加在上包装箱顶部以及侧壁、叠加在下包装箱底部为固定约束,其余均受到载荷的作用;
(3)两个包装箱叠加运输过程中,卡车运输包装箱正常时速以80 km/h行驶,运输过程中遇到紧急刹车状况。底部箱六点固定,底部箱顶叠加一个5.9 t顶部重量包装箱。研究此时导弹包装箱是否满足强度使用需要。根据三种工况条件,在后续计算求解过程中分别设置不同加载情况。
2 强度分析理论依据
包装箱承受载荷超过产品的极限强度时,就会发生故障,包装箱故障模式主要表现形式为:包装箱底座强度不足,底座较大变形;箱体框架断裂;包装箱发霉、漏水等[6]。可以用应力-强度模型分析其可靠度。
根据分布干涉图判断包装箱是否发生破坏,当分布没有重叠区域时,破坏不会发生,可以通过重叠区域面积的大小来判断包装箱的可靠度。定义可靠度R为:
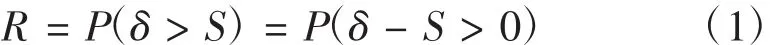
式中,δ为包装箱材料最大承载强度,S为包装箱所受到的应力。
图1中的重叠部分表示包装箱发生破坏区域。
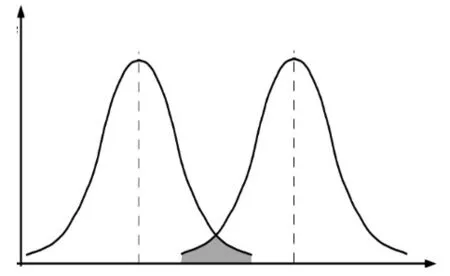
图1 应力-强度干涉图(阴影区域为故障发生区)
3 计算及结果分析
本文对包装箱建模进行了有效的简化,只保留了包装箱中的主要承重结构,以便提高计算效率[7]。包装箱的承力结构为框架形式[8]。云母板主要起绝热作用,铝蜂窝板具有抗高压、减震、隔音、保温、阻燃和比强度高等优良性能,包装箱主要承重结构为铝型材框架。对外表面铝合金框架简化包装箱初始模型如图2所示。

图2 包装箱铝型材框架模型
3.1 工况1情况下的强度分析
包装箱吊装处于稳态时,包装箱底受到44 000 N载荷作用,包装箱自重约为1.5 t。将包装箱简化结构模型进行网格剖分,其中最小单元质量为0.203 5,平均单元质量为0.604 7。在此包装箱简化模型中,共剖分网格单元96 459个,此包装箱结构网格剖分如图3所示。

图3 包装箱结构网格划分
在此工况下包装箱仿真分析结果如图4所示。
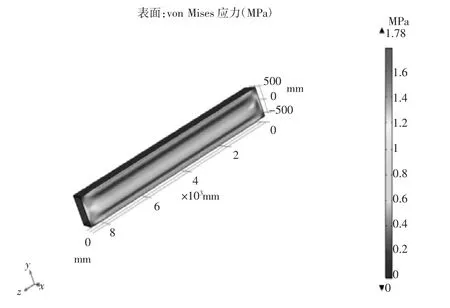
图4 包装箱铝型材框架受力分析云图
安全系数计算公式为:

根据COMSOL仿真结果,可计算出其安全系数约为3,所以当包装箱起吊在空中静止时,其包装箱铝型材框架具有足够的强度,满足设计要求。
包装箱在起吊瞬间具有垂直向下的加速度2g,利用软件仿真计算,包装箱铝型材框架受力云图如图5所示。
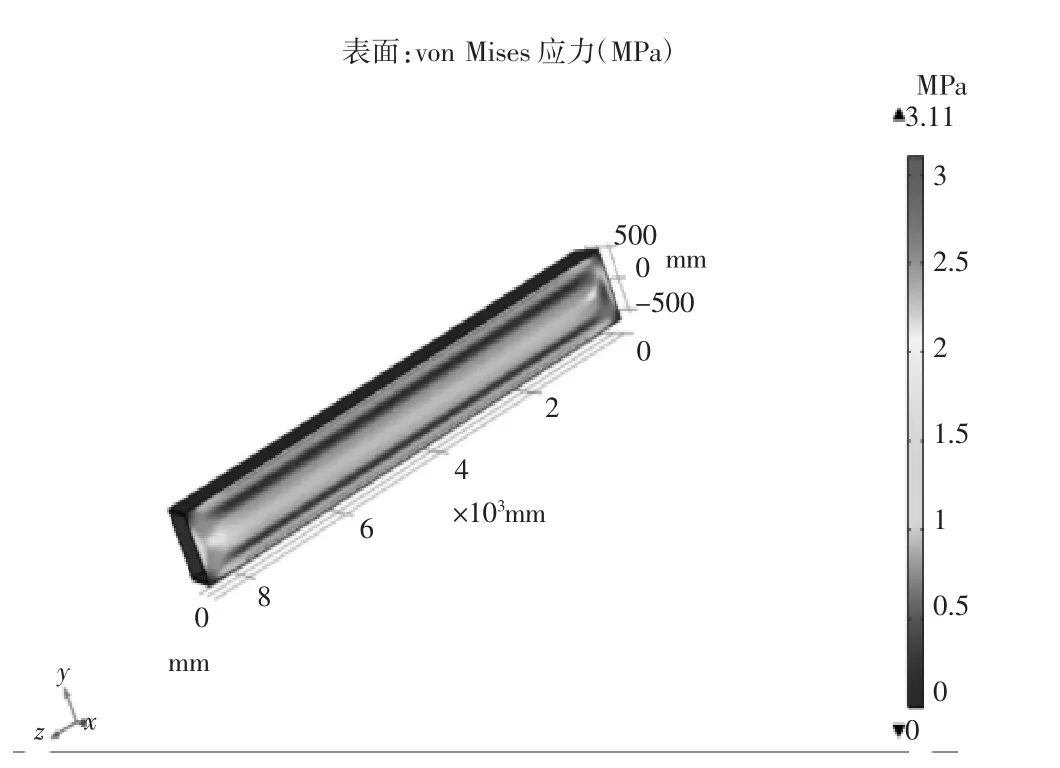
图5 起吊瞬间包装箱铝型材框架受力云图
从分析结果可知,在起吊瞬间受到2g的重力加速度时,其包装箱底部最大应力为3.11 MPa,包装箱是安全可靠的。
3.2 工况2情况下的强度分析
在工况二下,两个包装箱上下叠加,底部箱6点固定,上下锁紧,模拟包装箱叠加如图6所示。
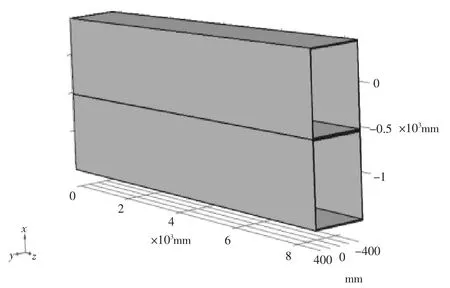
图6 包装箱叠加模型
对该包装箱叠加模型进行网格剖分,最小单元质量为0.002 629,平均单元质量为0.039 2。统计剖分网格单元61 424个,此包装箱叠加网格剖分如图7所示。
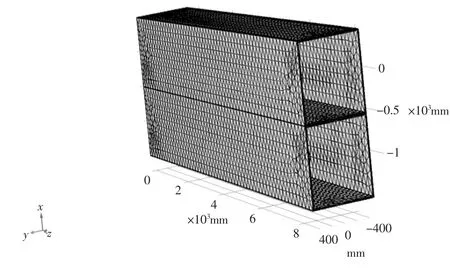
图7 包装箱叠加网格划分
包装箱在叠加时,其下包装箱顶部及侧壁支撑59 000 N的重力,因包装箱叠加静止不动,故其受到静载荷59 000 N。包装箱上下锁紧,其叠加部分其受到产品重力的作用。利用COMSOL软件对其进行受力分析,分析结果如图8所示。
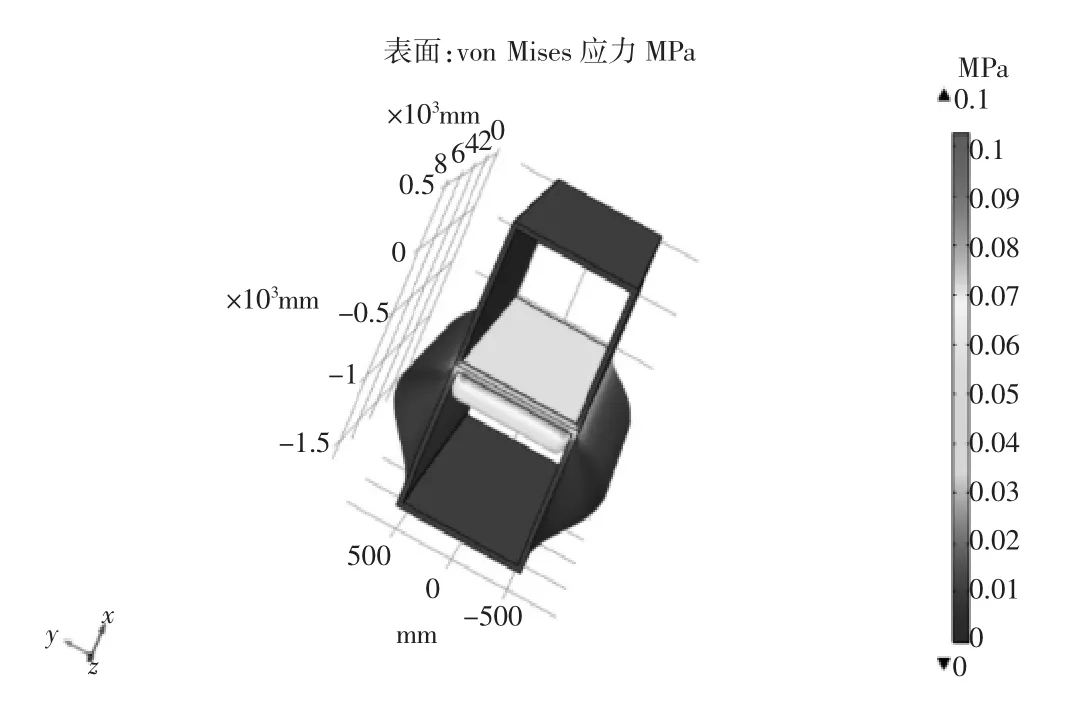
图8 包装箱叠加受力分析
图8 表明:包装箱最大受力为0.1 MPa,远远小于包装箱顶部和侧壁的强度极限,由式(1)可知,其应力远远小于包装箱材料强度,没有干涉区域,所以包装箱叠加时,包装箱的顶部以及侧壁满足使用载荷要求,整个结构是安全的。
3.3 工况3情况下的强度分析
模拟工况卡车运输包装箱正常80 km/h行驶过程中遇到紧急刹车状态。底部箱六点固定,底部箱顶叠加一个5.9 t顶部重量包装箱。载货车运输时给货体输入振动加速度:横向重力加速度不大于1g;纵向重力加速度不大于1g,法向重力加速度不大于1.5g(不含重力加速度1g);海运运输时给货体输入振动加速度,横向不大于1g,纵向不大于1.0g,法向不大于2g(不含重力加速度1g)。
在工况三情况下,其包装箱叠加简图如图7所示,其网格划分如图8所示。工况三分析结果如图9所示。
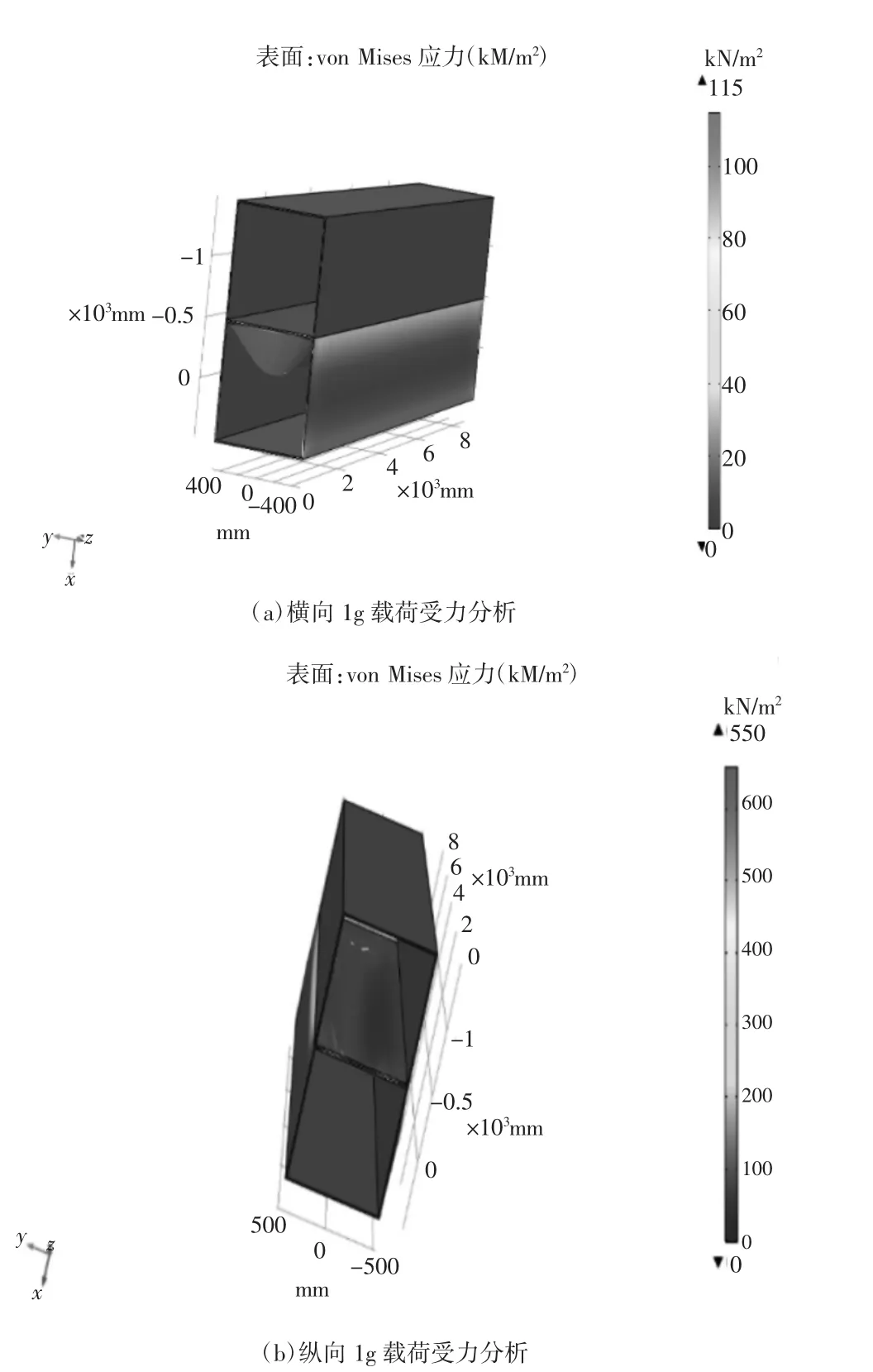
图9 工况三包装箱受力分析
由图(a)可知,包装箱横向方向受力最大为115 kN/m2,远远满足使用需求,整个结构是安全的;当包装箱受到纵向为1g的加速度冲击时,其分析结果如图(b)所示。包装箱叠加接触部分受最大应力为660 kN/m2,包装箱外部铝框架的强度为572 MPa,由式(1)可知,在此工况下,其最大受力远小于包装箱外部铝板、蜂窝铝板、云母板的强度极限,符合使用工况要求,包装箱安全。
包装箱上下叠加固定并受到法线方向2g的载荷冲击时,分析结果如图10所示。由受力图可知其载荷冲击最大为25.2 MPa,远小于包装箱铝板、铝蜂窝板、云母板的强度极限。
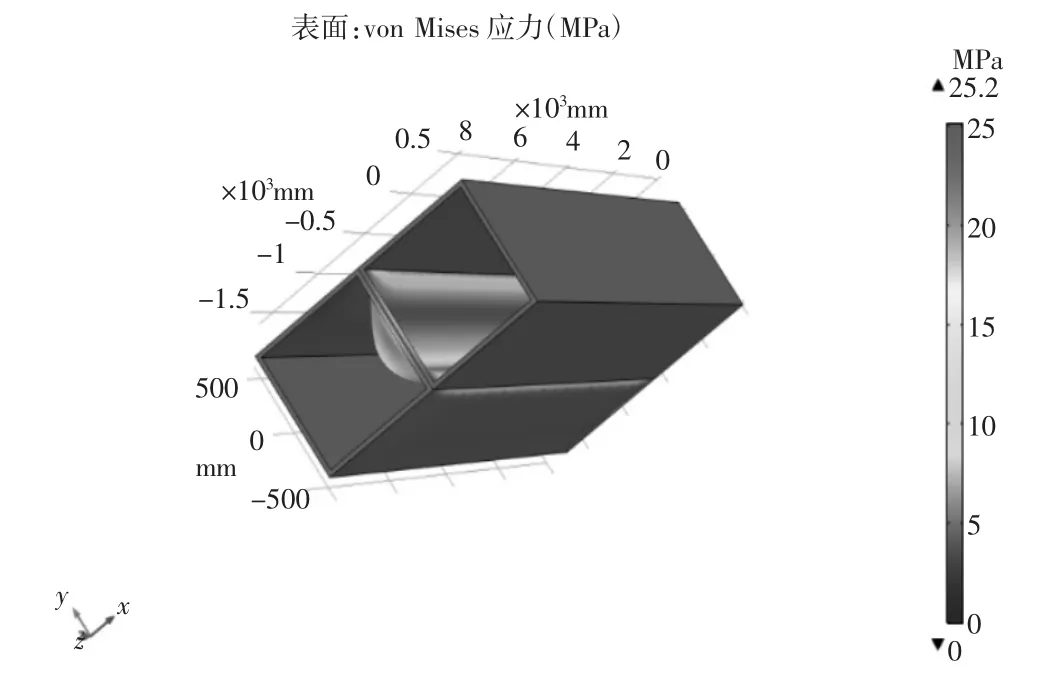
图10 包装箱叠加接触面受力分析
当包装箱上下叠加,采用M24内六角螺栓固定(六个点)时,在运输途中,螺栓受剪切力作用。由平衡方程计算螺栓剪力Fs:

式中:F1=m×a;实际计算中,假定各处的切应力相等,故受剪面切应力为:
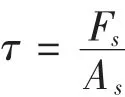
M24螺栓的剪切面积为353 mm2,将包装箱已知条件带入计算可得螺栓剪切力为167 MPa,已知M24高强度螺栓的屈服强度为940 MPa,小于其极限应力,故认为内六角螺栓时安全可靠。
包装箱处于45°倾斜稳态时,所受载荷为重力倍,83 439 N,包装箱倾斜情况如图11所示。由结果分析可知,此时其承受最大载荷为0.08 MPa,远远小于包装箱底部的强度极限,所以包装箱叠加时,包装箱的底部满足使用载荷要求,整个结构是安全的。

图11 包装箱45°倾斜
由结果分析可知,包装箱倾斜45°时,其最大受力为0.08 MPa,远远小于包装箱底部的强度极限,所以包装箱叠加时,包装箱的底部满足使用载荷要求,整个结构是安全的。
4 结束语
本文利用有限元软件COMSOL对某包装箱的结构强度进行计算分析,计算所模拟的工况为最大极限条件,在实际运输过程中出现的几率较小,该包装箱仍有一些其他工况下细节问题,有待于进一步研究;对某包装箱起吊、叠加、运输等载荷分布情况,利用COMSOL软件模拟进行仿真模拟计算,并对其结果应用应力-强度模型进行校核。经过分析得知,包装箱在吊装、海运、交通运输等工况条件下,强度满足使用要求,包装箱的结构是安全的。

