基于双圈图GA2指标的分析
刘晚乔,赵 飚
(1.中国国际航空股份有限公司新疆分公司,新疆 乌鲁木齐 830026)(2.新疆大学数学与系统科学学院,新疆 乌鲁木齐 830046)
对于分子的描述,在化学、物理和药理学等方面起着重要的作用[1]. 其中,一个能描述分子图的一些性质的数被称为拓扑指标,对于分子图的拓扑指标能反应分子的一些物理和化学性质,所以通过计算分子图的某种拓扑指标的数值,可以统计出分子的某些物理化学性质. 特别是在 QSPR/QSAR 研究中,发现了许多拓扑指标在化学中应用广泛[2-5].
设G是一个简单图,对于没有说明的术语和概念可参考文献[6-7].记图G的点集为V(G),边集为E(G),dG(u)(dG(v))为图G中点u(v)的度数.则图G的GA指标定义如下[8-9]:
令e=uv是图G的一条边,连接点uv,则定义:
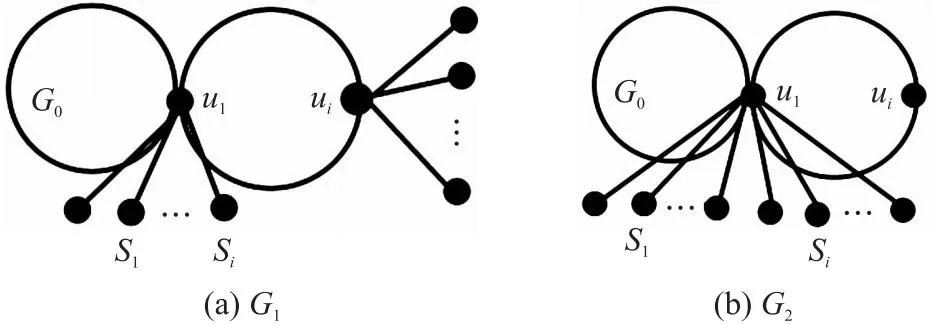
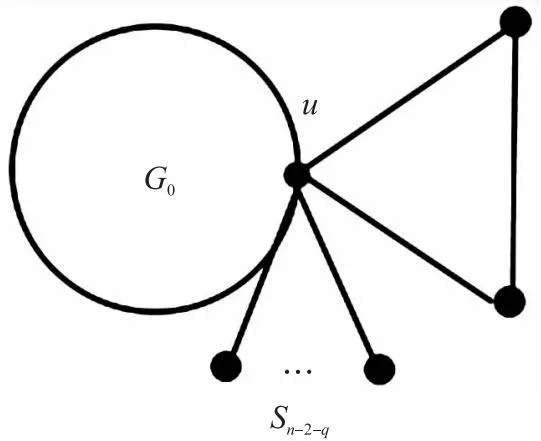
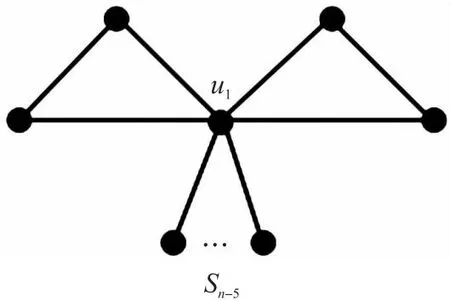
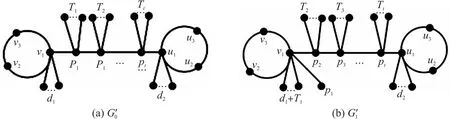
N(e,u,G)={x∈V(G)|dG(x,u) N(e,v,G)={x∈V(G)|dG(x,u)>dG(x,v)}, u的邻点记为NG(u),v的邻点记为NG(v)[10].同时 nu(e)=nu(e,G)=|N(e,u,G)|, nv(e)=nv(e,G)=|N(e,v,G)|, 式中,n(u)表示图G中的点到顶点u的距离小于到顶点v的距离的数目,n(v)同理. 2010年,文[11]定义了第二类拓扑指标GA2指标,定义如下: 同时,确定了完全图中的GA2指标上下界,以及树图中具有最小和最大GA2指标的树图,分别是星图和路.Tang等[12]在2011年巧妙采用了图变换的方法,进一步确定了树图中具有GA2指标第二大及第二小的图,同时得出了具有最大GA2指标和最小GA2指标的单圈图.本文主要描述了在n个顶点的双圈图中,利用图形的变换,进而确定具有最小GA2指标的图. 图G是一个连通双圈图,且有n个顶点,n+1 条边,下面将双圈图进行了3种分类: (1)当n≥5时,圈Cm,Cp共享一个公共点,见图(a). (2)当n≥6时,圈Cm,Cp中间连接一条长度大于等于1的路,见图(b). (3)当n≥4时,3条内部不相交的路P1,P2和P3具有公共的端点u,v,见图(c). 令G=(V,E)是一个双圈图,其中圈Cm和圈Cp的长度分别为q和p,且T1,T2,…,Tk(0≤k≤p+m)表示圈上悬挂的树,T1,T2,…,Tk为G-E(Cm,Cp)的非平凡分支.令N(Ti)=li,i=1,2,…,k,且l=l1+l2+…+lk=n-p-q+1,其中N(Ti)表示为树Ti点的个数,记双圈图为G=CG(T1,T2,…,Tk),则有下面的引理. 图1 双圈图主要分类 引理1若图G是一个有n个顶点,且n≥4的双圈图,则 G1=CG(S1,S2,…,Sk), G2=CG(P1,P2,…,Pk), 双圈图G1中,u1,u2,…,uk是圈Cm,Cp上的点,且S1,S2,…,Sk是点u1,u2,…,uk的悬挂边. 双圈图G2中,u1,u2,…,uk是圈Cm,Cp上的点,且P1,P2,…,Pk是点u1,u2,…,uk的悬挂路, 则可以得到 GA2(G1)≤GA2(G)≤GA2(G2), 式中,G=CG(T1,T2,…,Tk),N(Ti)=li(i=1,2,…,k). 为了找到双圈图中具有最小GA2指标的图,只需要考虑有悬挂边的双圈图. 图2 图G1变换到图Gi 证明将E(G1)里的边分成七部分,其表示为: (1)E1={e=uv∈Gi|degGi(v)=1,degGi(u)≥3}; (2)E2={e=uv∈Cp|d(u,u1) (3)E3={e=uv∈Cp|d(u,u1)>d(v,u1),d(u,ui)>d(v,ui)}; (4)E4={e=uv∈Cp|d(u,u1) (5)E5={e=uv∈Cp|d(u,u1)>d(v,u1),d(u,ui) (6)E6={e=uv∈Cp|d(u,u1)>d(v,u1),d(u,ui)=d(v,ui),d(u,u1)=d(v,u1),d(u,ui)>d(v,ui)}; (7)E7={e=uv∈Cp|d(u,u1) 根据GA2的定义,可以得到 (1) 当边uv∈E4时 所以,当边e∈E4,可以得到, (2) 同样对于边uv∈E5可以得到在图Gi中, 当边e∈E5,则有 (3) 对于连通图Gi,单圈图Cp的圈长p为奇数时,所有的边e∈Ej(1≤j≤5).由式(1-3)可得, GA2(G1)≥GA2(Gi). 当圈Cp的长度为偶数时,接下来考虑,当边uv∈E6时,则有 所以,当边e∈E6,则有 (4) 当边uv∈E7时,则有 所以,当边e∈E7,则有 (5) 由式(1)-(5)可得 由图G1转换的图Gi可以得到GA2(G1)≥GA2(Gi). 图3 图 图4 双圈图类型Ⅰ图 通过计算: 式中,t=[p/2],k=p-2t,d=n-q-p+1. 当p=2t(t≥2) 时, (6) 当p=2t+1 (t≥1) 时, (7) 当p=4和p=3时 (8) 图5 图变换到图 图6 图变换到图 即 (9) (10) 则 式中,S=d1+d2+l+t. 图7 双圈图类型Ⅲ 图1 引理

2 结果与分析
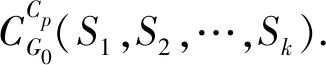
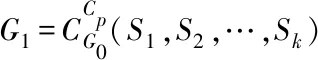
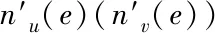
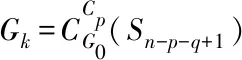

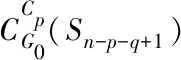
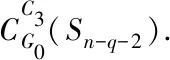
2.1 双圈图类型I
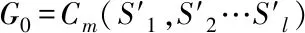
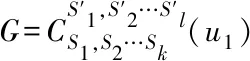

2.2 双圈图类型Ⅱ

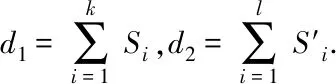
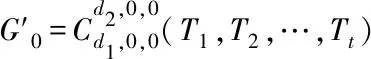
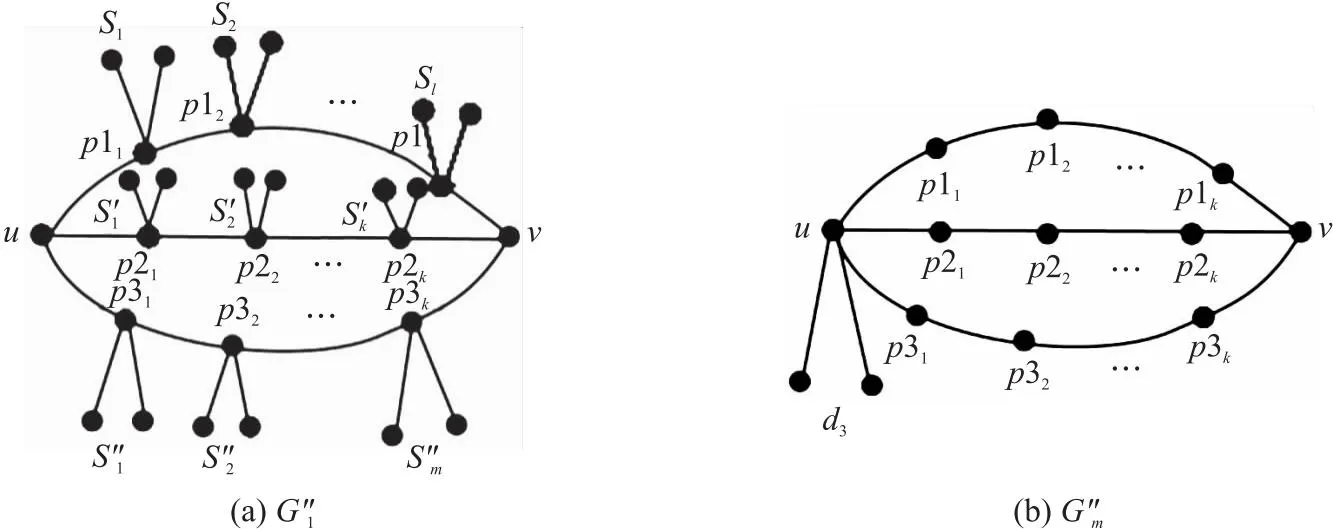
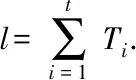
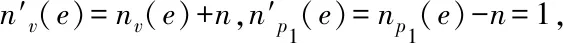

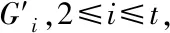
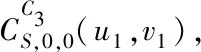
2.3 双圈图类型Ⅲ

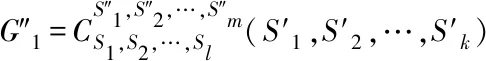
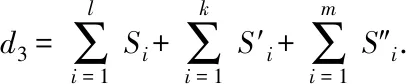
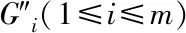
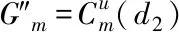
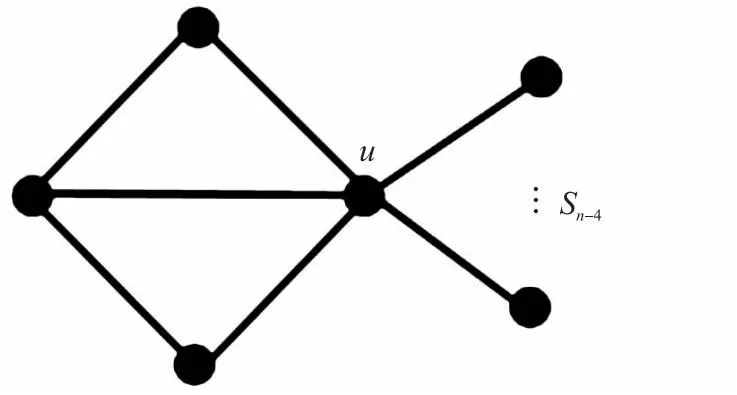
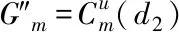
3 结论