基于量子蚁群算法的智能制造调度问题研究

吴昌钱,黄 锐,罗志伟

(1.闽南科技学院计算机信息学院,福建 泉州 366200)(2.北京理工大学计算机学院,北京 100081)(3.厦门大学机电学院,福建 厦门 361000)

随着我国科技的迅速发展,带动了高端制造业市场,相关设施装备的需求量也逐渐扩大. 先进的大型机械设备由各个重要的构件组成,这些构件的制造工艺复杂且加工精度非常高,因此,构件的制造过程是高端制造业的关键之处.

精密复杂构件的生产模式特点是典型的生产品种多,每种品种加工数量较少,交货周期长,成本高. 而且,精密复杂构件的制造工艺较为复杂,且加工的精度较高,加工工序不同,并且工件间无约束,但同一工件的工序有顺序[1]. 由此可见,制造车间调度问题(Aviation Manufacturing Job Shop Scheduling Problem,AMJSP)的特点与作业车间调度问题(Job Shop Scheduling Problem,JSP)的特点近似相等,因此,本文将AMJSP考虑为JSP. JSP对高端制造业的发展和进步的作用至关重要,如今的科技已较为发达,从而车间调度问题也逐渐复杂化,而传统模式车间调度方案已经无法高效解决JSP问题,因此相应的各种求解车间调度问题的智能算法应运而生,例如遗传算法(Genetic Algorithm,GA)、粒子群算法(Particle Swarm Optimization,PSO)等.

崔琪等[2]为了求解混合流水车间调度问题,提出了利用变邻域搜索的方式来改进GA,该方案可有效求解车间调度问题,但其收敛速度较慢. 刘洪铭等[3]提出了一种改进PSO算法的方案,该算法基于自适应权重,提高了粒子利用率,加入了混沌以平衡全局与局部,但其容易丢失种群多样性. 刘胜辉等[4]提出了一种双禁忌表禁忌搜索算法,该算法避免了在搜索中容易出现循环的情况,提高了寻优能力. 黄海松等[5]提出了一种改进模拟退火算法以求解双目标柔性JSP,该算法融合搜索与编码方法提高了运行速度,避免了传统的模拟退火算法陷入早熟,提高了算法的全局寻优能力. 施文章等[6]提出一种退火下布谷鸟算法求解JSP问题方案,该方案改善了种群的多样性. 上述智能算法各有各的特点,以不同程度的效率解决JSP问题,但是随着车间调度问题的复杂化加上算法的某些局限性,还需进一步对算法进行优化.

综上所述,本文根据复杂构件制造车间的特点,结合量子计算和蚁群算法提出一种基于量子蚁群算法的智能制造车间调度问题方案,该方案保留了量子计算的高效性,提高了蚁群全局寻优能力,避免了蚂蚁易陷局部最优解问题.

1 车间调度问题描述及数学模型

1.1 智能制造作业车间调度问题描述

在智能制造作业车间调度问题AMJSP当中,根据每个工件和每台机器的信息特点,研究如何安排n个工件在m台机器上的加工的顺序,使得最大完工时间最小. 其加工过程中的基本假设和约束条件为:

(1)加工时,不考虑员工、机器、用电等意外因素;

(2)计算加工时间,不加入材料运输、工件设备安装拆卸等时间;

(3)工件的设计工艺都是提前确定好的,都是零时刻到达;

(4)工件工序按照工序顺序加工且过程不中断,对应的机器都是提前确定好的;

(5)一个机器同时只对一个工件的一道工序且该工序只能由该机器完成.

1.2 数学模型

基于上述问题描述和约束条件,建立JSP的数学模型,并构造相应的矩阵. 从上述描述可知,一般概括有n个工件,m台机器,每个工件最多有m道工序,则对JSP问题的参数的集合分别有:

(1)n个工件的工序集合为J=(J1,J2,…,Jn)T,其中Ji=(ji1,ji2,…,jik,…,jnm)T,i∈[1,n],k∈[1,m],jik表示第i个工件的第k道工序.相应地,工件的工序排列矩阵J:

(1)

(2)n个工件加工使用的机器集合为M=(M1,M2,…,Mn)T,其中Mi=(mi1,mi2,…,mik,…,mnm),i∈[1,n],k∈[1,m],mik表示为第i个工件的第k道工序所加工的机器.相应地,工序所需机器的加工机器矩阵MJ为:

(2)

(3)n个工件的各个工序加工时间的集合为:T=(T1,T2,…,Tn)T,其中Ti=(ti1,ti2,…,tik,…,tnm),i∈[1,n],k∈[1,m],tik表示第i个工件的第k道工序加工所需要的时间.相应地,工序的加工时间矩阵TJ为:

(3)

综上所述,在智能制造车间调度问题中,给定工件的工序矩阵和相应的生产时间矩阵,求出最短生产时间的目标函数公式定义为:

min[max(Tx)].

(4)

根据上述的约束条件和矩阵,可得出相应的约束公式为:

Cij-Kij-tij=0,

(5)

式中,1≤i≤n,1≤j≤m.式(5)对应的约束条件是工件工序对应的机器是确定的,按照工序顺序加工且过程不中断.Cij是指工件的完工时间.

Kij+tij≤Ki(j+1),

(6)

式中,1≤i≤n,1≤j≤m.式(6)对应的约束条件是加工的工序按着一定的顺序开始进行.

Kijq+tij≤Kweq,

(7)

式中,1≤i≤n,1≤j≤m.式(7)对应的约束条件是一个机器同时只能进行一个工件的一道工序且该工序只能由该机器完成.Kweq是指加工w工件的第e道工序在机器q上的进行生产的开始时间.

2 量子蚁群算法的优化机理

量子蚁群算法(Quantum Ant Colony Algorithm,QACA)是由量子计算和蚁群算法结合而成的,以量子计算[7-9]为基础,可以提高蚁群全局寻优能力,避免蚂蚁易陷局部最优解问题.

2.1 量子计算

在QACA中,量子比特对信息素进行编码,它是一个二维复向量空间中由标准正交基{|0〉,|1〉}所组成的向量单位,其状态可表示为|ψ〉=|α〉+|β〉,其中α和β满足|α|2+|β|2=1,表示|0〉和|1〉的概率幅.通过利用量子旋转门来改变相位可以实现对量子比特的状态改变,其表示式为(8):

(8)

2.2 量子蚁群算法基本思想

根据文献[10-12]提出的基于蚁群的启发式进化算法,可得蚂蚁k转移相邻节点的概率为式(9):

(9)

图1 量子蚁群算法流程图

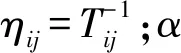
信息素强度更新方程为:

τij(new)=(1-ρ)τij(old)+Δτij(k),

(10)

(11)

式中,τij(new)表示蚂蚁移动的下一个节点;ρ为信息素的挥发性,0≤ρ<1;τij(old)表示蚂蚁所在当前的节点;Q为常数.

综上所述,量子蚁群算法流程为:

步骤1:蚂蚁利用转移概率移动节点;

步骤2:计算各个蚂蚁目标函数最优值;

朗读能够训练普通话的发音技巧。学生在一定的量的朗读训练之后可以达到吐字清晰，语音响亮，琅琅上口，悦耳动听；能通过语音传达出文章所表达的感情。

步骤3:利用量子旋转门、信息素强度方程式更新;

步骤4:若当前满足迭代次数,则输出最优解,否则返回步骤1.

3 基于量子蚁群算法的制造车间调度问题求解

将量子蚁群算法(Quantum Ant Colony Algorithm,QACA)应用到求解制造车间调度问题当中,根据工件的工序的加工时间矩阵TJ,可构造一个有向图,如图2所示.在图2中,蚂蚁从左边的开始处开始向ti1移动,下一个移动节点为tij(new),其可移动节点集合表示为:

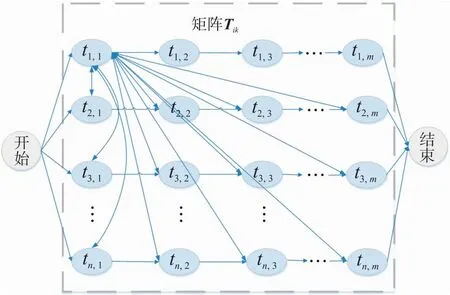
图2 基于量子蚂蚁的AMJSP有向图

tij(new)={tpq||i≠p}.

(12)

蚂蚁横向移动时,只能向相邻的右节点进行移动,向其他节点移动时,移动到的节点不约束.直至蚂蚁移动到结束.其中,蚂蚁移动过的节点不可能重复移动.

其算法实现步骤如下.

步骤1:初始化,设置各个参数值,其中,蚂蚁数与机器数m相同,最大迭代次数DDmax,信息素τij(0)=1,蚂蚁量子信息素编码所有αij和βij初始值都设置为2-1/2.设置基于量子蚂蚁的AMJSP有向图,共n×m个节点.

步骤2:在开始处放入n个蚂蚁,最终蚂蚁向结束节点移动.节点移动的概率为式(9).

步骤3:设置每个蚂蚁所走的节点数组Ak[n×m],即第k个蚂蚁所走的节点放入数组中.根据式(9)和式(12)设置可选节点数组Kk[n×m],即第k个蚂蚁还未走过的路径节点的集合.

步骤4:如果蚂蚁走完所有节点,则计算出该蚂蚁的目标函数值即最短完工时间,记录当前最低值,否则,执行步骤2.

步骤5:根据式(8)改变量子信息、式(10)和式(11)改变轨迹信息素强度.

步骤6:若当前满足迭代次数DDmax,则输出最优解,否则执行步骤2.

4 实验结果与分析

关于JSP求解若干典型问题,国内外学者专家设计了不同参数,以便测试比较各自的优化性能[13],如表1所示.

表1 不同参数的JSP调度案例

在众多案例中,关于JSP运用最多的是LA类和FT类,因此,本文选择该两类数据案例对基于量子蚁群算法的求解制造车间调度问题进行性能测试. 为了更好的评估,实验平台为Windows 10,CPU i7,8G内存,Matlab R2018b仿真软件,其他实验仿真环境相关参数如表2所示.

表2 实验参数

首先对FT06案例进行调度寻优,将所提方案对其进行求解得到的最优解,如图3所示. 可以看出,基于量子蚁群算法的FT06寻优效率比较快,在执行4次后就可得到最优解,在执行5次的时候就可得到平均解,从此可见,量子蚁群算法在制造车间调度的收敛性能上有优势,最优解为55.

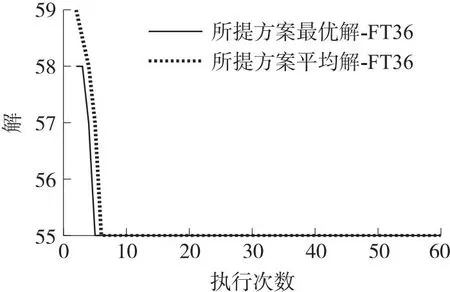
图3 基于QACA-AMJSP的FT06寻优解过程

将QACA-AMJSP与GA方案[14-15]、PSO算法方案[16-18]在FT06案例上进行对比,如图4所示. 可以看出,GA方案的收敛速度较慢且低于PSO方案的收敛速度,而QACA-AMJSP方案的算法收敛速度最快. QACA-AMJSP方案在执行4次时,达到了最优解55. GA在执行6次的时候,达到了最优解58,PSO方案在执行次数到7次时,最优解也达到了55,但总体而言,与GA和PSO方案相比,QACA-AMJSP方案的全局寻优能力较强,收敛速度较快.

图4 与其他方案的FT06最优解对比图

然后对LA36案例进行调度寻优,将所提方案对其进行求解得到的最优解,如图5所示. 可以看出,基于量子蚁群算法的LA36寻优效率比较快,在执行23次后就可得到最优解,在执行24次的时候就可得到平均解,由此可见,量子蚁群算法在制造车间调度的收敛性能上有优势,最优解为1 268.

图5 基于QACA-AMJSP的LA36寻优解过程

将QACA-AMJSP与GA方案、PSO方案在LA36案例上进行对比,如图6所示. 可以看出,GA方案的收敛速度较慢,远低于PSO方案的收敛速度,而QACA-AMJSP方案的算法收敛速度最快. GA在执行24次的时候,达到了最优解1 574,QACA-AMJSP方案在执行23次时最优解达到了1 268,PSO方案在执行次数到24次时,最优解也达到了1268,但总体而言,与GA和PSO方案相比,QACA-AMJSP方案的全局寻优能力较强,收敛速度较快.

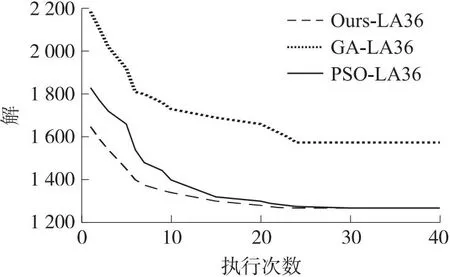
图6 与其他方案的LA36最优解对比图

5 结论

提出量子计算与模拟自然界蚁群行为的蚁群算法相结合求解智能制造车间调度问题. 根据智能制造车间的特点,构建了相应的车间调度数学模型. 然后利用量子蚁群算法求解AMJSP,提高了蚁群全局寻优能力,避免了蚂蚁易陷局部最优解问题. 实验结果表明,相比GA和PSO,量子蚁群算法对解决智能制造车间调度问题具有较高的搜索效率和较快的收敛速度. 但是未来智能制造车间会逐渐复杂化,复杂构件的加工精度会越来越细,还需要人工全程参与,因此,下一步研究将人员因素考虑到智能制造车间调度问题中进行求解.