基于多尺度地理加权回归的建成环境对通风潜力的影响研究——以武汉市主城区为例

杨佳明,安 睿,仝照民,刘艳芳

(武汉大学资源与环境科学学院,湖北 武汉 430079)

随着城市化的快速推进,城市内部出现许多密集的高层建筑,阻碍了城市内部的空气流动,常导致热岛效应[1]、空气污染[2]等“城市病”的出现,严重威胁人体健康. 为了解决这些问题,多个城市例如北京[3]、广州[4]、成都[5]等将城市通风廊道(urban ventilation corridor,UVC)的建设纳入国土空间规划等政策体系中,这为城市通风研究提供了契机. 城市通风潜力是UVC建设的基础与前提,在城市的可持续发展与生态文明建设中的地位日益重要. 城市的建成环境会显著影响城市通风潜力,如建筑会阻碍通风效率,而以绿地、水域为主的地表可以提供风力廊道[6]. 因此,模拟城市通风潜力并讨论建成环境对其影响机制具有潜在价值.

传统的城市通风潜力模拟方法多用风洞试验、计算流体力学(computational fluid dynamics,CFD)、气象研究与预报(weather research and forecasting,WRF)模型. 风洞试验[7]与CFD[8]仅适用于小范围建筑群通风模拟,虽然它们的模拟精度较高,但研究结论难以推广至城市尺度. WRF对风环境模拟结果精度一般大于1 km,适合大范围城市群风场模拟,但其计算复杂,导致模型的不确定性,需要对模拟结果进行修正[9-10]. 运用地理信息系统(geographic information system,GIS)技术可以对城区尺度的通风状况进行分析,该方法计算成本低,且具有普适性[11]. 近年来,Xie等[12-13]以武汉市为研究区,在传统GIS数值模拟的基础上,扩展了基于电路理论的通风潜力模拟方法,模拟结果可以直观展示高精度的城市通风潜力.

已有研究发现,建筑物的形态和布局[14]、蓝绿空间的配置[15]等建成环境指标与通风潜力显著相关,如街道高宽比、建筑密度、天空开阔度等;此外,城市自然邻域对通风潜力的影响不容忽视,如归一化差异植被指数(normalized difference vegetation index,NDVI)[16]、改进的归一化差异水体指数(modified normalized difference water index,MNDWI)[17]和地形起伏度[18]等. 多数研究采用传统的线性回归分析讨论驱动机制,但该模型未考虑因变量的空间异质性;地理加权回归(geographically weighted regression,GWR)虽然考虑了空间异质性,但忽略了不同自变量的影响尺度差异. 江颖慧等[19]研究发现地表温度(land surface temperature,LST)和NDVI的空间自相关具有尺度效应并表现出明显的季节差异. An等[20]利用多尺度地理加权回归(multi-scale geographically weighted regression,MGWR)证实建成环境因子对公交通勤占比的影响存在尺度效应.

综上所述,本研究以武汉市主城区为研究区,基于电路理论模拟城市通风潜力,结合建筑数据、三调数据和遥感数据等,构建基于3Ds(density,diversity,design)的通风潜力影响因素指标体系,在详细对比GWR与MGWR的结果的基础上,讨论建成环境对通风潜力影响的空间非平稳性和尺度效应,为城市通风环境的改善提供实证基础.

1 研究区域、数据及方法

1.1 研究区概况

武汉是湖北省省会,地处江汉平原东部、长江中游,市内江河纵横、湖港交织,水域面积占全市总面积四分之一. 武汉属北亚热带季风性(湿润)气候,降雨多集中在6—8月,雨热同期、四季分明. 由于近年来城市的迅速扩张,截至2018年底,武汉市建成区面积为723.74 km2,常住人口达1 108万人. 本研究选取武汉主城区为研究区域(图1),该区域人口集中、建筑密集,有必要研究其通风潜力,以期构建城市通风廊道缓解夏季形成的城市热岛效应.

图1 研究区范围

1.2 数据来源及处理

本研究搜集了建筑轮廓数据、遥感影像、气象监测、土地利用、人口栅格、道路网络等多源数据,基准数据时点为2018年. 其中建筑轮廓矢量数据采集自百度地图,属性包括每栋建筑高度、投影面积等. 利用中分辨率成像光谱仪(moderate-resolution imaging spectroradiometer,MODIS)产品中8天合成的地表反射率产品MOD09A1(500 m分辨率),选取2018年6、7、8月轨道号为h27v05和h27v06的影像,并进行影像预处理、去除异常值、裁剪和拼接等处理. MODIS数据来源于美国地质勘探局官网. 气象数据来源于美国国家气候数据中心的公开FTP服务器,包括每小时的风向、风速等. 本研究将360°风向角分为16个方向,计算各方向3个月(6、7、8月)内平均风向频率,在风玫瑰图(图2)中将最大风向频率视为该季节(夏季)主导风向,并作为后续研究基础. 经计算,该主导风向为东北风.

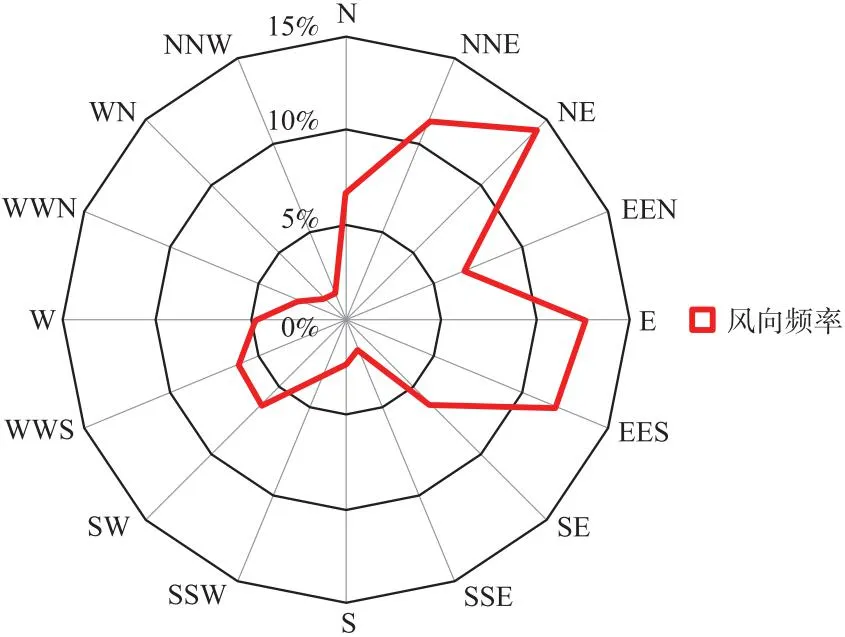
图2 武汉市2018年夏季平均风向频率

人口栅格数据收集自WorldPop,分辨率为100 m. 土地利用(第三次全国国土调查)和道路网络数据均由武汉市测绘院提供,其中,土地利用数据包括公园与绿地、河流水面等在内的43种二级类用地(30 m×30 m),路网数据包括国道、省道、县道、乡道等四级道路.

1.3 模型构建

1.3.1 通风潜力计算

城市冠层中的空气团在遇到城市中的建筑时会形成分流,这恰好与在由节点和电阻组成的电路网络中电流的分流高度相似. 在电路中,由欧姆定律I=U/R可得,当一定的电压U施加到电阻R时,通过的电流I取决于电阻R的大小. 电路相关术语对应的城市通风相关概念如表1所示.

表1 电路理论术语的通风相关概念解释

为保证研究区边界与建成区之间有较大缓冲范围,需要以市中心为圆心,建立半径为40 km的圆形缓冲区,区内电阻率默认为1(保证无建筑区域电阻值为0),然后运用电路理论,将空间数据转化为栅格图像,计算每个像元阻力值,根据Xie等[12]的研究,该阻力值用建筑迎风指数(frontal area index,FAI)[21]表示,相当于气流阻力,电流值即表示通风潜力. 考虑建筑物的密集程度,每一个像元代表一个节点,相邻节点由电阻连接. 电导率G用通风指数(ventilation index,VI)表示. FAI与VI公式如下:

其公式解释如图3所示.

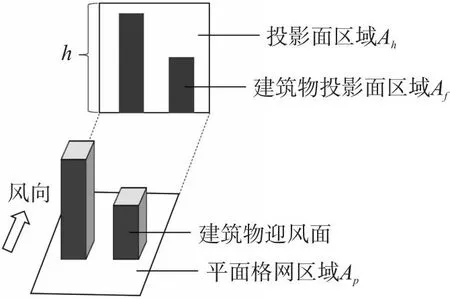
图3 FAI与VI公式解释

1.3.2 自变量选取

对于城市的建成环境,有研究表明城市地表通风潜力与建筑高度、容积率和粗糙度长度有明显负相关关系[22-23],也有研究表明天空开阔度(skyviewfactor,SVF)与城市通风潜力有正相关关系[24],而城市蓝绿空间、道路和城市地形等对城市通风潜力也有一定的贡献作用[25].随着Ewing等[26]提出建成环境5Ds指标体系,有大量关于居民出行方式与建成环境之间相关性的研究,鉴于此,本研究采用基于3Ds的指标体系,探究建筑及其周围环境与城市通风潜力之间的相关性,其中各个变量的相关解释如表2所示,其空间分布特征如图4所示.所有影响因子的栅格数据均采样至 500m×500m的空间分辨率,以保持进一步分析的空间一致性.

表2 基于3Ds的指标体系

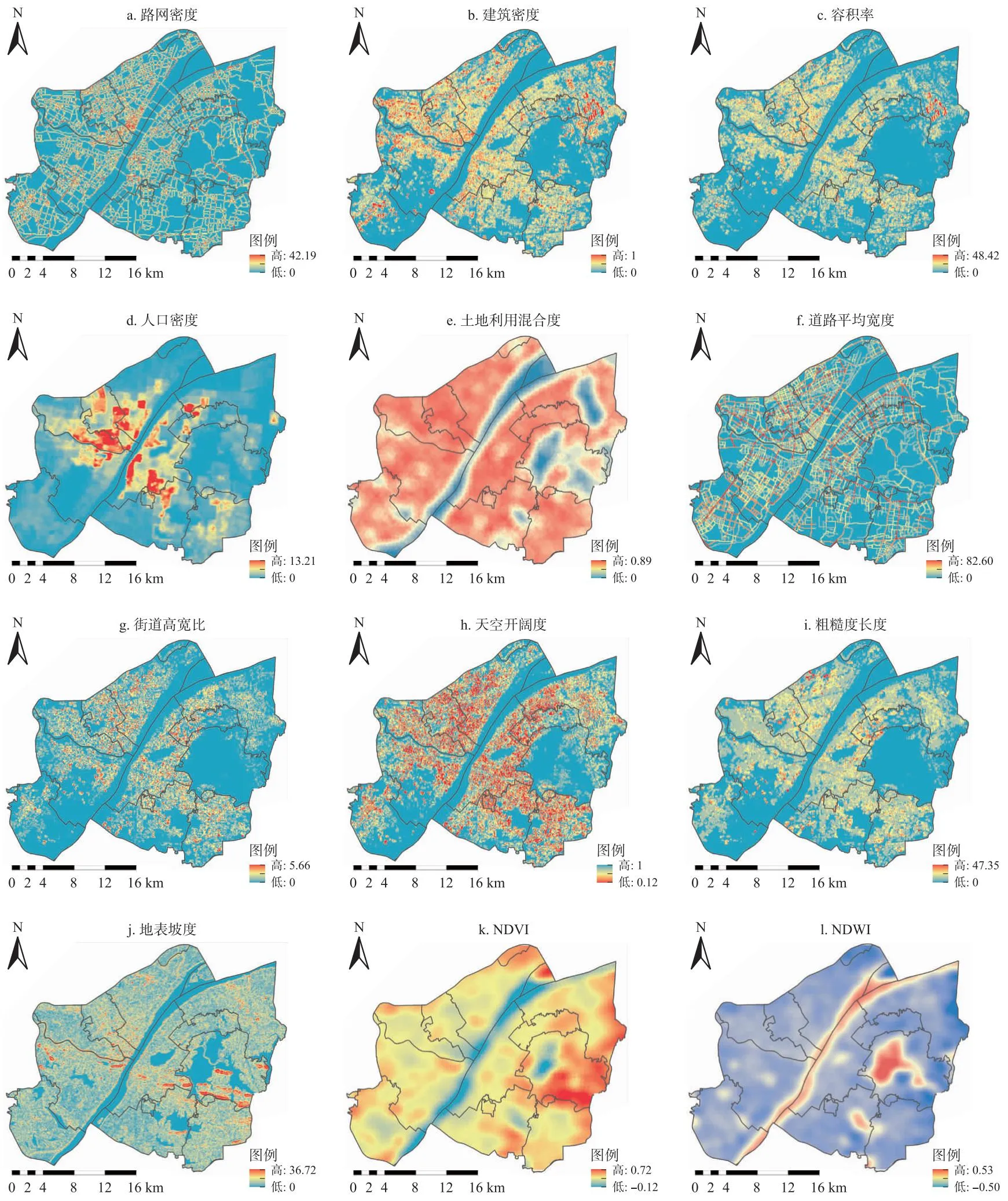
图4 各自变量空间分布特征

1.3.2.1 密度

本研究根据建筑数据,考虑每个城市通风单元的路网密度、建筑密度、容积率和人口密度.有研究表明,道路密度与温度分布范围呈负相关,与最小温度呈正相关[27],而温度也从侧面反映了通风能力;来风方向建筑越少、密度越小,通风潜力越大[28];容积率对风速有影响,并且与通风潜力呈负相关[22];人群的集聚与城市热环境之间有关联[29].热环境与风环境密不可分,因此本研究将人口密度作为反映城市通风潜力的指标,经计算,其值在0～13.21之间.

1.3.2.2 多样性

根据武汉市测绘院提供的2018年“三调”土地利用数据,本研究将与通风潜力相关的5类用地用来测算土地利用混合度[30],包括商业服务业用地、工矿用地、住宅用地、公共管理与公共服务用地、其他用地(包括水域、林地等用地类型). 经计算,土地利用混合度在0～0.89之间.

1.3.2.3 设计

Wang等[25]对通风潜力的定量分析研究表明,道路宽度>50 m是对城市通风潜力影响较大的因素. 本研究计算了每个城市通风单元的道路平均宽度,经计算,其值在0～82.60之间.

根据He等[31]对城市通风性能的研究,街道高宽比影响周围气流运动的位置与形态,当街道与盛行风的夹角小于30°时有利于通风. 刘勇洪等[14]认为街道高宽比与天空开阔度密切相关. 本研究计算了每个城市通风单元的街道高宽比,经计算,其值在0～5.66之间.

天空开阔度是描述三维城市形态的指标,表达了城市空间的封闭程度,是重要的城市形态学参数,并且对城市的通风潜力有重要影响. 根据Li等[24]的研究,天空开阔度与空间平均风速比有显著的线性正相关关系. 本研究采用Zakšek等[32]提出的基于数字高程模型(digital elevation model,DEM)的栅格计算模型估算天空开阔度,经计算,其值在0.12～1之间,城区内大部分地区的天空开阔度较低.

表面粗糙度长度反映了城市下垫面的不均匀性,Fang等[17]运用粗糙度长度与天空开阔度构建了通风阻力系数,并以此表征城市通风状况. 本研究运用Grimmond等[33]提出的形态学模型对城市粗糙度长度进行计算,其值在0～47.35之间. 虽然粗糙度长度的计算过程涉及高度,并受到土地利用类型的影响,但粗糙度长度和土地利用类型作为影响通风潜力的重要因素[6,34],仍有必要单独分析二者与通风潜力的关系,尤其是二者对通风潜力影响的空间异质性.

1.3.2.4 自然邻域

根据Kim等[18]的实验研究,地形对地面10 m以上的风速有影响,表现为随着坡度的增加而增加. 本研究根据DEM计算了每个城市通风单元的地表坡度,结果在0～36.72之间.

城市的绿地和水体一直被认为是城市通风廊道的冷源. Fang等[17]将NDVI和MNDWI作为最低成本路径(least cost path,LCP)分析中的两个成本因素对城市通风廊道性能进行研究. 本研究计算了每个城市通风单元的NDVI与NDWI,结果分别在-0.12～0.72和-0.50～0.53之间.

1.4 模型方法

普通最小二乘法(ordinary least squares,OLS)模型作为一种全局回归模型,其公式如下:

式中,i代表第i个城市通风分析单元(500 m×500 m),i∈{1,2,…,n};yi是模拟城市通风潜力的电流值;βj是第j个解释变量的系数,j∈{1,2,…,k};xij是第i个城市通风分析单元的第j个解释变量;εi代表误差值.本研究n=2 780,k=13(包括一列常数项).每个解释变量参数估计可以用矩阵形式表示:

β=(XTX)-1XTy,

式中,X是解释变量的矩阵(n,k),y是模拟城市通风潜力的电流值的观测值,β为各解释变量的回归系数估计值,其为整个研究区域内的平均值,不能反映回归参数的真实空间特征.

相比OLS,GWR与MGWR考虑了因变量与解释变量之间的空间非平稳性,并为每个回归点设置单独的回归方程,根据其他数据点的不同位置,考虑到数据点和回归点的空间距离,对各数据点赋予权重,距离越近,权重越大. GWR的公式如下所示:

式中,βij是第j个局部参数;(ui,vi)表示第i个通风分析区域格网中心点坐标.每个城市通风分析单元的解释变量参数估计可以用矩阵形式表示:

βi=(XTWiX)-1XTWiy,

式中,βi表示第i个城市通风分析单元局部参数估计的向量(k,1),Wi是在位置i处的对角空间权重矩阵(n,n).这种方法是一种核回归的广义概念,其内核是一个距离衰减函数,用于确定权重随距离减小的速度.这里使用高斯函数来计算权重,其公式如下:

式中,Wiu是从第u个城市通风分析单元到第i个城市通风分析单元的权重;diu是从第u个城市通风分析单元中心到第i个城市通风分析单元中心的距离;b表示第j个变量的回归系数使用的带宽,不同的带宽选择直接影响参与局部回归的邻域点的数量与权重.

GWR与MGWR的带宽搜索一般选择黄金分割搜索,带宽选择通常使用更正的Akaike信息标准(corrected Akaike information criterion,AICc). GWR虽然考虑了因变量与解释变量之间的空间非平稳性,但是它对所有的解释变量采用固定带宽,这简化了每个协变量的观测值通常在不同空间尺度上产生变化的过程. MGWR通过使用基于通用加性模型(generalized additive model,GAM)[35]的后退拟合算法(back-fitting algorithm)为每个解释变量使用不同的优化带宽,这允许每个自变量拥有各自不同的空间平滑水平,解决了GWR模型所有变量同一平滑水平的缺陷,降低了估计的偏误,从而反映了各自空间过程的空间作用尺度,产生了比GWR更接近真实和有用的空间过程模型. 因此,带宽对于 GWR 中的所有解释变量都是恒定的,但在 MGWR中随着j的变化而变化.

2 结果与讨论

2.1 结果

由表3可知,根据OLS模型回归结果,除了路网密度、建筑密度和地表坡度,其余变量均与城市通风潜力显著相关. 道路宽度越宽、NDWI越高,城市通风潜力越大. 相反,城市冠层粗糙度长度越大、人口越密集、建筑容积率越高、土地利用类型越混合、街道高宽比越大、天空开阔度越大、NDVI越高,城市通风潜力越小. 模型调整后的R2是0.463,AICc是6 178.781. 显然,该模型的解释能力并不高,因此,本研究运用GWR和MGWR模型来获得局部关系.

表3 OLS模型回归结果

首先,应检验 OLS、GWR 和 MGWR 模型的整体效果. 本研究测试了各模型的空间自相关拟合残差. 如图5所示,对比3种模型的全局莫兰指数(Moran’sI)与P值,OLS与GWR模型的Moran’sI和P值为正,MGWR的Moran’sI为负. 这表明,MGWR能更好处理空间自相关问题. 并且由表4所示,MGWR拟合残差的残差平方和(residual sum of squares,RSS)为689.18、均方根误差(root mean square error,RMSE)为0.50、AICc为4 786.42,均为3个模型中最小. 由此说明,MGWR的拟合损失最小.

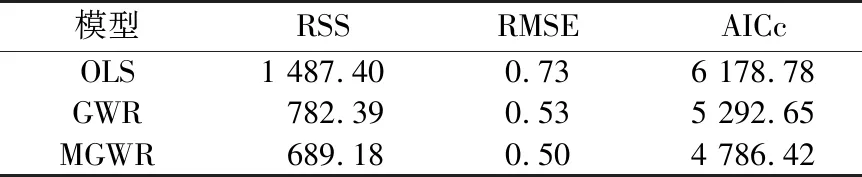
表4 3种模型误差对比

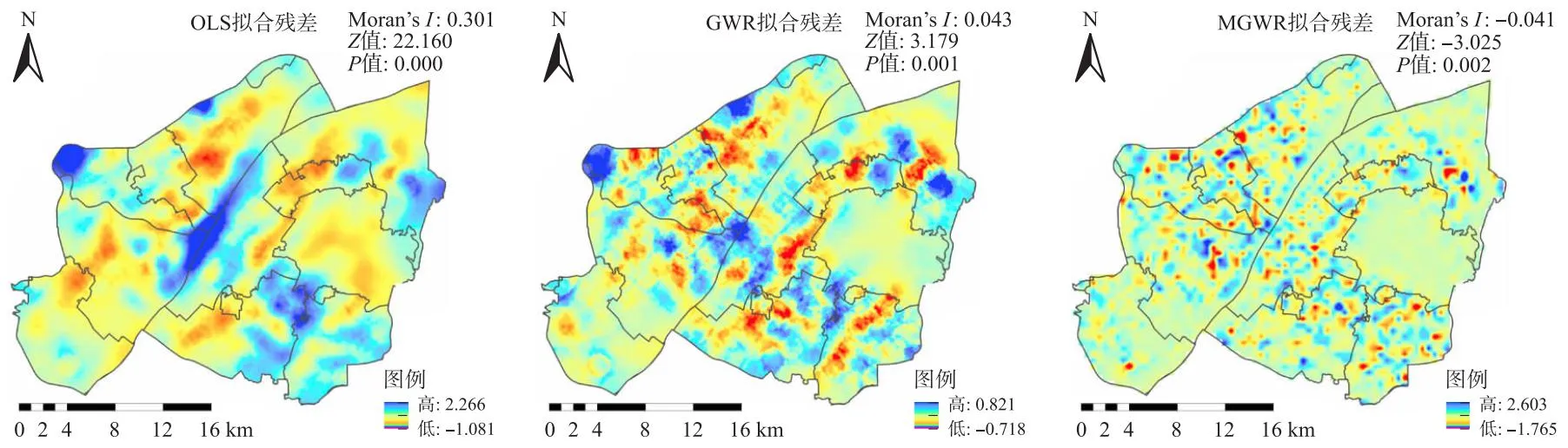
图5 3种模型空间自相关特征

其次,根据GWR和MGWR模型的局部R2(图6),MGWR的局部区域细节表现比GWR更为明显,高值区域更高,低值区域更低.

图6 GWR与MGWR局部拟合空间分布特征

总体而言,MGWR模型拟合误差小于GWR和OLS,并且可以更好地反映武汉市主城区通风潜力与其影响因素之间的关系.

由表5可知,本研究各城市通风影响因素的GWR模型带宽都为211,仅占所有城市通风分析单元的7.59%. 对于MGWR模型,人口密度、街道高宽比、天空开阔度和粗糙度长度的带宽分别为2 761、1 465、2 779 和348,都高于GWR的固定带宽211,并且它们的最小值与最大值无符号反转,但在GWR模型中其最大值与最小值存在符号反转,这与它们与通风潜力呈现显著负相关关系的预期相矛盾,这可能是由于带宽过小、过度拟合而数据系数变异过大导致的. 由此说明,MGWR的估计结果更加可靠.

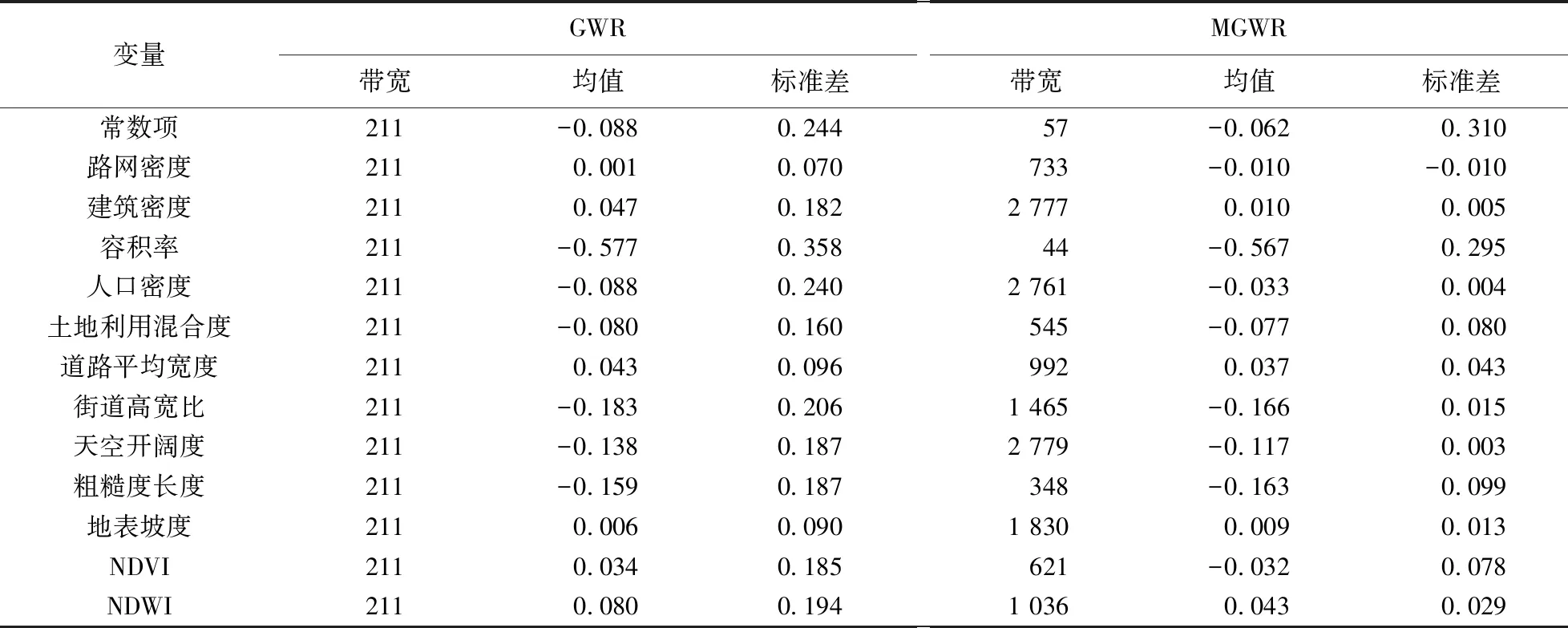
表5 GWR与MGWR系数对比

MGWR回归结果根据带宽可分为3个尺度(图7):

图7 各自变量GWR与MGWR系数空间分布对比

(1)局部尺度(带宽在44～621之间). 容积率(图7a),其GWR结果除汉阳区南部、江岸区北部、武昌区北部、东湖东部和洪山区以外,其余地区均与通风潜力呈显著负相关,汉南区南部负相关程度最大,系数最低为-3.075. 但其MGWR模型的带宽为44,显著负相关区域比GWR更大,仅在汉阳区南部和洪山区不显著,且存在符号反转,系数最高为0.359,在汉南区南部和北部、武昌区中部、江汉区南部和东湖高新区南部与通风潜力呈显著负相关,系数最小值为-1.965. NDVI(图7h),其GWR结果在汉阳区东南部、硚口区东南部、江汉区南部、江岸区南部、武昌区中部、东湖南部、东湖高新区南部和东部与通风潜力呈显著负相关,系数最低为-0.481,在硚口区西部、汉阳区西北部、江岸区西北部、洪山区和青山区南部与通风潜力呈显著正相关,系数最高为0.754. 相比GWR,其MGWR带宽为621,在武昌区西部、汉阳区东部、硚口区东部、江汉区东南部和江岸区南部与通风潜力呈显著负相关,系数最低为-0.222,在硚口区西部和汉阳区西北部与通风潜力呈显著正相关,系数最高为0.174. 粗糙度长度(图7g),其MGWR结果除汉南区、武昌区中北部、江岸区北部、洪山区和青山区中西部以外,其他区域均与通风潜力呈显著负相关. 土地利用混合度(图7c),其MGWR结果在长江沿岸区域与通风潜力呈显著负相关.

(2)区域尺度(带宽在622～1 465之间). 道路平均宽度(图7d),其GWR结果在江汉区、硚口区北部、汉阳区中东部、武昌区北部和南部、洪山区北部与通风潜力呈显著正相关,系数最高为0.415,在汉南区北部、江岸区北部和洪山区部分地区与通风潜力呈显著负相关,与研究预期相反,在青山区、洪山区、江岸区、东湖周边地区、汉南区和汉阳区南部存在异常低值,系数最低为-0.216. 相比GWR,其MGWR带宽为992,在硚口区、汉阳区中北部、江汉区、武昌区中南部和洪山区与通风潜力呈显著正相关,硚口区正相关强度最大,系数最大为0.143,其在青山区与通风潜力呈负相关,与研究预期相反. NDWI(图7i),其MGWR结果在武昌区西部、汉阳区东北部、硚口区东南部、江汉区和江岸区南部与通风潜力呈显著正相关. 街道高宽比(图7e),其MGWR结果在全区域与通风潜力呈显著负相关.

(3)全局尺度(带宽接近2 780). 该尺度下MGWR几乎将所有样本加入回归,系数变化范围较小. 天空开阔度(图7f),其GWR结果在汉南区北部、汉阳区东部、洪山区北部、东湖高新区和青山区东部与通风潜力呈显著负相关,系数最大值为0.248,最小值为 -0.739,存在符号反转. 相比GWR,其MGWR带宽为 2 779,全区无系数符号反转,其系数最大值为 -0.112,最小值为-0.121,并且与通风潜力呈显著负相关,全区呈现由西南至东北负相关强度逐渐增强的趋势. 人口密度(图7b),其MGWR结果除硚口区、江汉区和江岸区西部以外,其余地区均与通风潜力呈显著负相关,全区呈现由西北至东南负相关强度逐渐增强的趋势.

2.2 讨论

(1)局部尺度(带宽在44～621之间). 该带宽下的因子有容积率(图7a2)、粗糙度长度(图7g2)、土地利用混合度(图7c2)和NDVI(图7h2). 根据表3,它们均与通风潜力呈负相关,但刘勇洪等[14]发现城市地表通风潜力与容积率和粗糙度长度呈正相关关系,这一差异主要是由通风潜力的识别方法不同造成的. 传统研究多基于通风阻力系数(ventilation resistance coefficient,VRC)模型识别通风潜力,该方法依赖天空开阔度和地表粗糙度指标,易受数据异常值影响;本研究采用电流值大小表征通风潜力,不受除FAI和风向以外因素的干扰,将传统的内生变量调整为驱动因子. 容积率高的区域建筑密度与人口密度也较高,规划中应限制区域容积率以增强通风潜力[36]. 洪山区的粗糙度长度较大,而通风潜力较低,虽然存在较大面积水域,但周边建筑密集形成较大风阻,影响了水域的冷源作用,需要补充建设通风廊道. 长江沿岸土地利用混合度与通风潜力呈强负相关,作为金融商贸核心区,该区域商住混合的高层建筑较多,显著阻碍了通风潜力. 硚口区西部和汉阳区西北部的NDVI与通风潜力呈强正相关,大面积绿地为通风提供了便利. 但在长江沿岸呈强负相关[16],这是由于区域内街边绿地、公园绿地与小区绿地面积小而分散,难以形成长距离的通风走廊,应适当推进蓝绿空间连片化发展.

(2)区域尺度(带宽在622～1 465之间). 该带宽下的因子有道路平均宽度(图7d2)、NDWI(图7i2)和街道高宽比(图7e2). 根据表3,街道高宽比与通风潜力呈负相关,道路平均宽度和NDWI与通风潜力呈正相关. 硚口区道路平均宽度大且多数道路朝向与风向相似,形成了较好的道路通风廊道,但需注意该地区车行带来的负面效应. 长江与汉江交汇区及江汉区中部的NDWI与通风潜力呈强正相关,因其水源的下风向建筑稀疏,充分发挥了水体冷源作用,提供了良好的通风廊道. 街道高宽比在汉南区的负相关强度最大,该地区需要在规划中注意街区内建筑物的间距和高度,采取离散化的建筑配置以疏导气流[36].

(3)全局尺度(带宽接近2 780). 该带宽下的因子有人口密度(图7b2)与天空开阔度(图7f2),它们的系数变异较小. 人口密度与城市通风潜力在东湖高新区呈强负相关,开发区内人口密集且建筑较高,更容易形成局部热岛. 天空开阔度在全区与通风潜力呈显著负相关[14],但Li等[24]发现SVF与以风速比表示的通风潜力呈正相关,这一差异是由通风潜力识别方法不同造成的.

3 结论

本文利用电路理论模型模拟2018年武汉市主城区夏季主导风向的通风潜力,综合构建3Ds指标体系,从密度、多样性和设计描述建成环境,同时考虑了自然邻域. 详细对比了OLS、GWR和MGWR的回归结果. 相比于OLS模型,GWR虽然考虑了空间异质性,但模型中每个变量的带宽是相同的,难以体现不同变量在空间上影响范围的区别,并且带宽较小时,会使得所有变量的系数有较多的异常值与符号反转,与预期相关性相矛盾. MGWR采用的自适应带宽解决了这些问题,可以得到更加合理与稳定的结果. 根据MGWR提供的带宽,本文将不同自变量的影响尺度划分为局部、区域和全局3个尺度,充分体现其空间异质性.

本文为城市通风潜力的优化提供了实证启示. 但是也存在一定的局限性,MGWR的回归仍然为线性结果,并未考虑建成环境因子对通风潜力的非线性影响,后续考虑使用梯度提升决策树(gradient boosting decision tree,GBDT)等非线性模型进一步探索分析. 此外,可考虑对不同气候类型下的不同城市开展相关试验并进行验证,使其在城市规划中更具通用性.