边染色 9-临界图边数的新下界

李 梅, 田大东

(中国矿业大学 理学院,江苏 徐州 221116)

边染色 9-临界图边数的新下界

李 梅, 田大东

(中国矿业大学 理学院,江苏 徐州 221116)

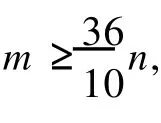
临界图;边数;下界;度

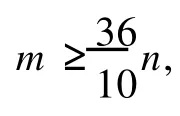
Key words:critical graphs;size of edge;lower size;degrees

0 引 言

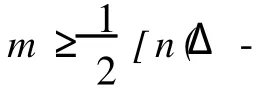
文中讨论的图都是有限、无向的简单图。有限图是指图的点集、边集都是有限集;无向图是指图的边均为无向边;简单图是指无环且无多重边的图。有关的定义或符号可参考文献[2]。

1 预备知识

定义 1设 G是一个图,用 d(v)、V(G)、E(G)、Δ(G)、δ(G)、δ1(x)、m及 q分别表示 G的顶点的度数、顶点集、边集、最大度、最小度、x相邻顶点的最小度数、边数及平均度。

定义 2若对图 G的任何边 e,令 G′=G-e,如果χ′(G′)<χ′(G),则称 G是临界的。若 G是临界的且Δ(G)=Δ,则称 G是Δ-临界图。其中,χ′(G)表示图 G边色数。

引理 1[3](Vizing邻接引理) 设 G是Δ-临界图,xy∈E(G),d(x)=k,则 y至少有Δ-d(x)+1个Δ度邻点。

引理 2[4]设 G是Δ-临界图,xy∈E(G),且d(x)+d(y)=Δ +2,则有 :

(1)x、y的所有邻点 (除去 x、y)均为Δ度点;

(2)与 x、y距离为 2的顶点的度至少为Δ-1;

(3)当 d(x)、d(y)<Δ时,与 x、y距离为 2的顶点的度为Δ。

引理 3[4]设 G是Δ-临界图,Δ≥5,d(x)=3,则 x至少有两个Δ度邻点,它的顶点中除了 x外其余的点的度都大于等于Δ-1。

引理 4[5]设 G是Δ-临界图,d(x)=4,若Δ≥6,则有:

(1)若 x邻接一个Δ-2度顶点,则 x的其他邻点均为Δ度顶点;

(2)若 x的邻点全是大于等于Δ-1度顶点,并且其中一个邻接 3个小于等于Δ-2度顶点,则 x的其他 3个邻点只邻接一个小于等于Δ-2度顶点,即x;

(3)若 x邻接两个Δ-1度顶点,则 x的两个Δ度邻点只邻接一个小于等于Δ-2度顶点,即 x。

引理 5[6]设 G是Δ-临界图,d(x)=4,x有一个Δ-1度邻点,设为 w。如果 w(除 x外)还邻接一个Δ-1度顶点,则 x的其他三个邻点均为Δ度顶点,并且每一个Δ度顶点的邻点度均大于等于Δ-1。

引理 6[4]设 G是Δ-临界图,d(x)=5,如果有一个Δ-2度邻点 w,则有:

(1)如果w除了 x外还邻接一个小于等于Δ-2度顶点,则 x的其余的四个邻点均为Δ度顶点,并且除了 w外,所有邻点的度均大于等于Δ-1;

(2)如果 w仅有一个小于等于Δ-2度邻点,即x,则 x有三个大于等于Δ-1度邻点 (至少包括两个Δ度点)满足:Δ度顶点最多与两个小于等于Δ-2度顶点相邻,Δ-1度点仅与一个小于等于Δ-2度顶点相邻,即 x。

引理 7[5]设 G是Δ-临界图,xy∈E(G),z∈N(x)y,d(x)<Δ,则有:

τ(y,x,z)≥2Δ -d(x)-d(y)+1。

其中,τ(y,x,z)表示 z的邻点中 (不包含 x)度数大于等于 3Δ-d(x)-d(y)-d(z)+2的顶点数。

引理 8[6]设 G是Δ-临界图,d(x)=6,δ1(x)表示 x的最小度邻点的度数,如果δ1(x)=Δ-2或δ1(x)=Δ-1,则有两种情形。

情形 1δ1(x)=Δ-2,

(1)如果这个最小度邻点与三个小于等于Δ-2度顶点相邻,那么 x的其他 5个邻点全部都是Δ度顶点,且这些Δ度邻点仅与一个小于等于Δ-2度顶点相邻,即 x;

(2)如果这个最小度邻点与两个小于等于Δ-2度顶点相邻,则 x有四个大于等于Δ-1度邻点 (至少包括两个Δ度顶点)满足:Δ度顶点最多与两个小于等于Δ-2度顶点相邻,Δ-1度顶点仅与一个小于等于Δ-2度顶点相邻,即 x;

(3)如果这个最小度邻点与一个小于等于Δ-2度顶点相邻,即 x,则 x的所有Δ度顶点最多与三个小于等于Δ-2度顶点相邻。

情形 2δ1(x)=Δ-1,

(1)如果这个最小度邻点与四个小于等于Δ-3度顶点相邻,那么 x的其他 5个邻点全部都是Δ度顶点,且这些Δ度邻点仅与一个小于等于Δ-2度顶点相邻,即 x;

(2)否则,x的所有Δ-1度邻点最多只能与三个小于等于Δ-3度顶点相邻。

2 主要结果

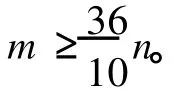
证明 运用 Discharging方法,按照差值转移规则 (差值规则大部分是根据临界图的邻接性质得到的)对相邻的顶点之间进行差值转移,使得最终的所有顶点的值都能满足要求。

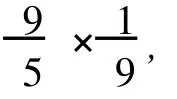
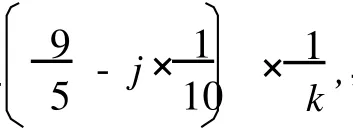
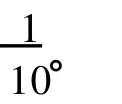
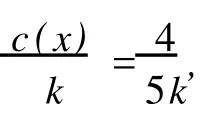
(1)对 d(x)=2的点,

设 x是一个 2度点,x邻接两个Δ度顶点,设为u、v,由引理 2,u至少邻接 7个不同于 v的Δ度顶点,v同样如此,则根据规则 1,有

(2)对 3≤d(x)≤7的点,

如果 d(x)+δ1(x)=Δ+2,设 y为 x的度数为δ1(x)的一个邻点,根据引理 2,x邻接 d(x)-1个Δ度顶点,考虑到 x、y可能同时邻接某些个Δ度顶点,所以这些Δ度邻点至少向 x转移差值:

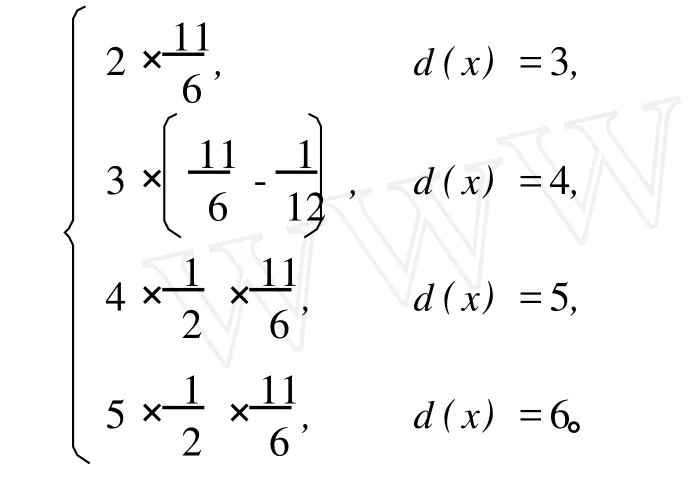
经过差值转移所得新值为

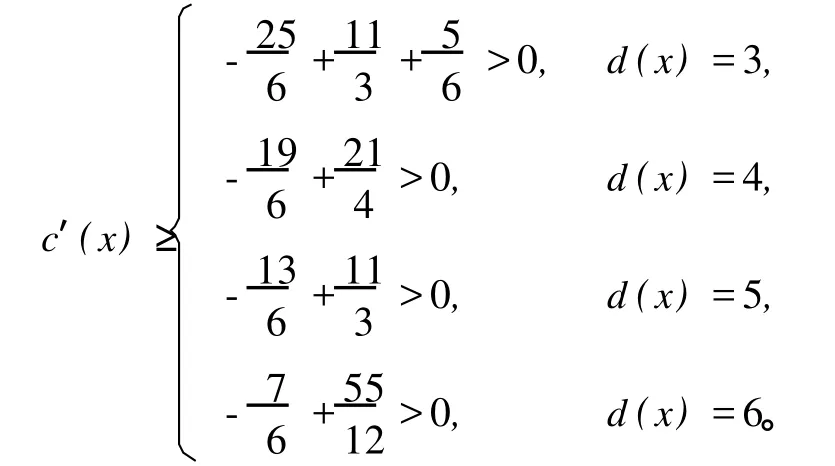
下文对各点只从 d(x)+δ1(x)≥Δ+3情况开始考虑。

(3)对 d(x)=3的点,

(4)对 d(x)=4的点,

如果δ1(x)=8,分两种情形来进行讨论:

情形 1x有一个 8度邻点,设为 w,再分两种情况。

(i)w除 x外还邻接一个小于等于 8度点,则由引理 5知,x的其他三个邻点均为Δ度点,且它们的邻点度数均大于等于 8,则所以由规则 2,得

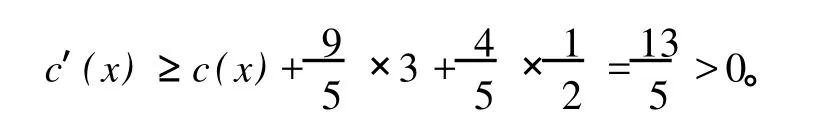
(ii)w除 x外不与任何小于等于 8度点相邻,则由引理 4,如果 x(除 w外)的三个Δ度邻点中有一个与三个小于等于Δ-2度点相邻,则其余两个Δ度点的邻点的度数均大于等于 8,由规则 2知

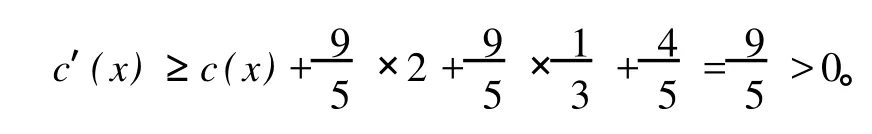
否则,x的所有邻点最多邻接两个小于等于Δ-2度顶点,此时

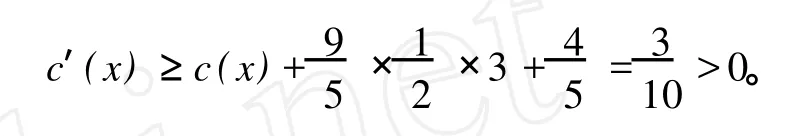
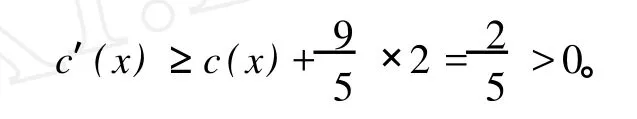
如果δ1(x)=9,根据引理 4分两种情形来进行讨论:

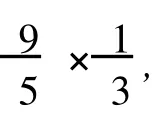
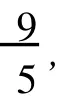
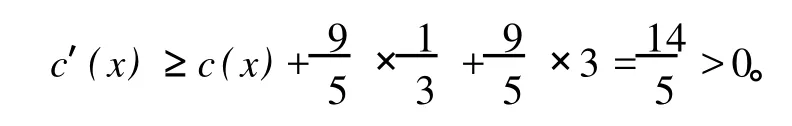
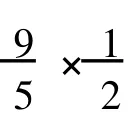
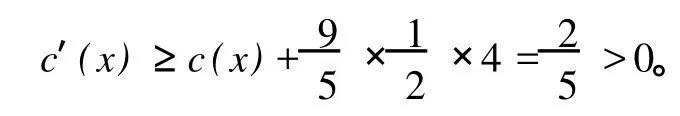
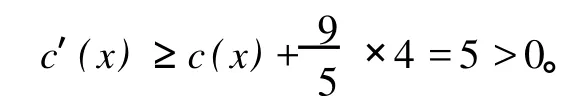
情形 2如果w仅有一个小于等于Δ-2度邻点,即 x,则 x有三个大于等于Δ-1度邻点 (至少包括两个Δ度点)满足:Δ度顶点最多与两个小于等于Δ-2度顶点相邻,Δ-1度点仅与一个小于等于Δ-2度顶点相邻,即 x。所以

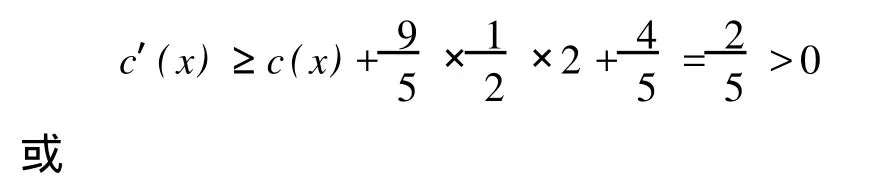
(5)对 d(x)=5的点,

如果δ1(x)=7,设 x的这个 7度邻点为 w,则根据引理 6分两种情形来讨论。

情形 1 w除了 x外还邻接一个小于等于Δ-2度顶点,则 x的其余的四个邻点均为Δ度顶点,并且这些Δ度邻点除了 x外,所邻接的点的度均大于等于Δ-1,所以

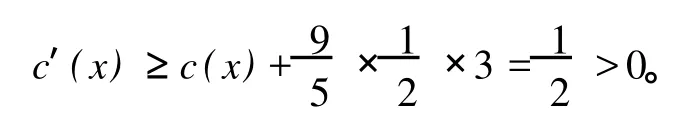
如果δ1(x)=8,分三种情形来讨论:

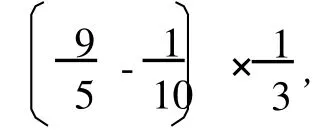
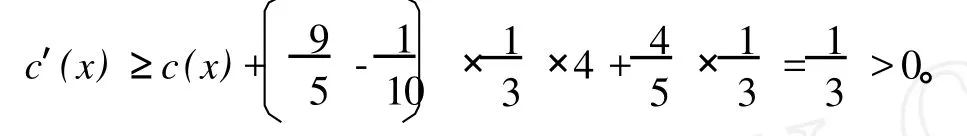
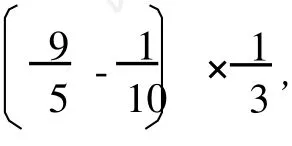
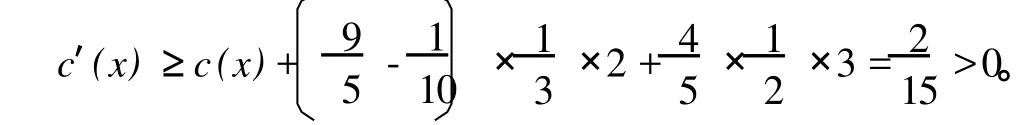
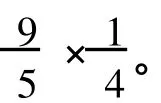
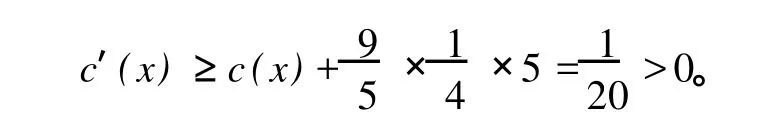
(6)对 d(x)=6的点,

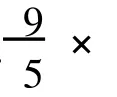
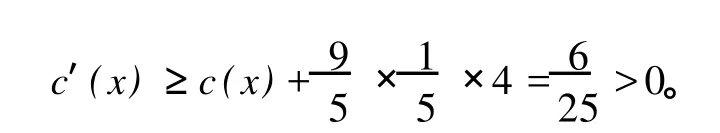
如果δ1(x)=7,设 x的这个 7度邻点为 w,则根据引理 8分三种情形来讨论:

情形 1w邻接三个小于等于Δ-2度顶点,则x其余的邻点均为Δ度顶点,且这些Δ度点除了 x外,所邻接的点的度均大于等于Δ-1,则由规则 2,

情形 2如果w邻接两个小于等于Δ-2度点,则 x有四个大于等于Δ-1度邻点 (至少包括两个Δ度点)满足:Δ度顶点最多与两个小于等于Δ-2度顶点相邻,Δ-1度点仅与一个小于等于Δ-2度顶点相邻,即 x。所以

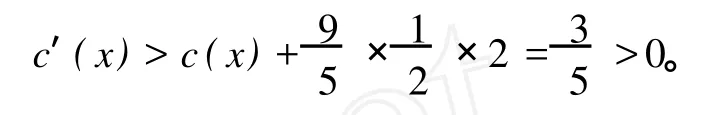
情形 3w仅邻接一个小于等于Δ-2度顶点,即 x,则 x的每一个Δ度邻点至多邻接三个小于等于Δ-2度顶点,所以

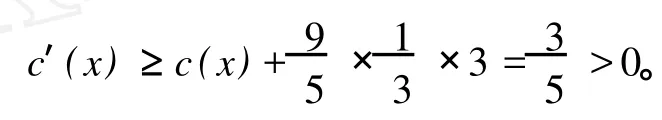
如果δ1(x)=8,分四种情形来讨论。

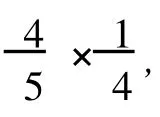
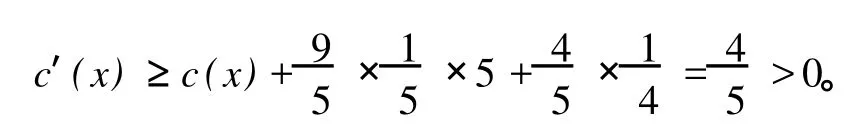
情形 2x有两个 8度邻点,则

情形 3x有三个 8度邻点,则

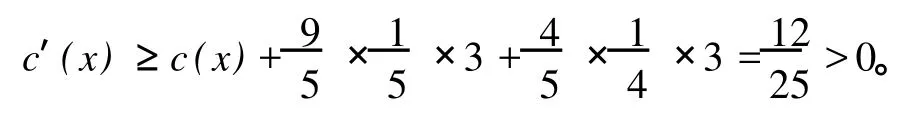
情形 4x有四个 8度邻点,则

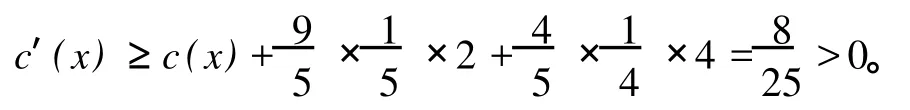
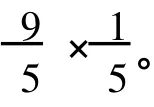
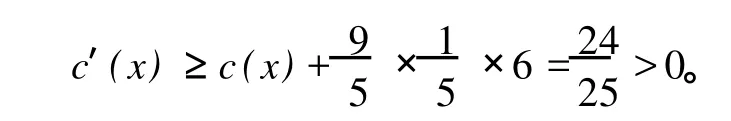
(7)对 d(x)=7的点,则由引理 3,x至少邻接两个 9度顶点,所以

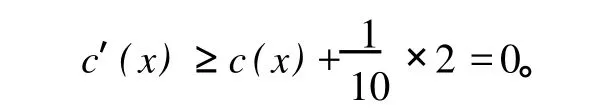
(8)对 d(x)=8的点,根据规则 4,可得

c′(x)≥0。

(9)对 d(x)=9的点,如果δ1(x)=2,则由规则1,可得

c′(x)≥0。

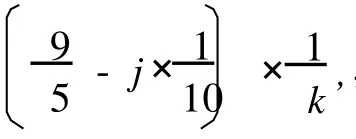
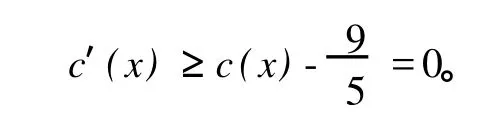
证毕。

3 结束语

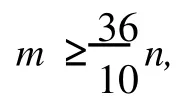
[1] YAP H P.On critical graphs with respect to edge colorings[J].DiscreteMath,1981,37(1):289-296.

[2] 邦 迪.图论及其应用[M].北京:科学出版社,1984.

[3] V IZI NG V G.Critical graphs with a given chromatic class[J].DiskretAnaliz,1965(5):9-17.

[4] ZHAO YUE.New lower bounds for the size of edge chromatic critical graphs[J].J.Graph Theory,2004,46(2):81-92.

[5] WOODALL D R.The average degree of an edge-chromatic critical graph[J].J.Graph Theory,2007,56(3):194-218.

[6] L I SHUCHAO,L IXUECHAO.Edge coloringof graphswith small maximum degrees[J].Discrete Mathematics,2009,309(14):4 843-4 852.

[7] 曲积彬.最大度为 9和 10时边染色临界图的下界[J].黑龙江科技学院学报,2007,17(6):479-482.

(编辑 王 冬)

New lower bound for size of edge chromatic critical graphs with max imum degree 9

L IM ei, TIAN Dadong
(College of Sciences,China University ofMining&Technology,Xuzhou 221116,China)

O157.5

A

1671-0118(2010)05-0406-05

2010-05-17

李 梅 (1984-),女,山东省临沂人,硕士,研究方向:计算数学,E-mail:wenwen5566ly@sina.com。