用粘合的方法研究一类新的整和图
石端银, 徐 晶, 丛凌博
(黑龙江科技学院 理学院,哈尔滨 150027)
用粘合的方法研究一类新的整和图
石端银, 徐 晶, 丛凌博
(黑龙江科技学院 理学院,哈尔滨 150027)
为进一步完善整和图理论,采用顺序标号法给出龙虾树的一种整和标号。利用粘合的方法证明了有公共顶点的一系列多重龙虾树也是整和图。该结论不但推广了整和图类型,也为树的理论研究提供了依据。
整和图;粘合;龙虾树
Abstract:This paper is an attempt to further improve the theory of integral sum graph by introducing an integral sum labeling of the lobster tree through sequential labeling method.The paper features the method of identification to prove that a series of multiple lobster trees with the public vertex is integral sum graph.This conclusion notonly promotes the type of integral sum graph,but also provides a basis for the theoretical study of the tree.
Key words:integral sum graph;identification;lobster tree
0 引 言
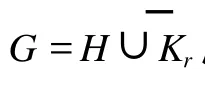
1 基本概念
定义 1 两个图 G1=(V1,E1)和 G2=(V2,E2),假设点 r1∈V1是 G1的一个固定顶点,称其为 G1的根,r2∈V2是 G2的根,令 (G,r)=(G1,r1)∞(G2,r2)表示图 G的根 r,且点 r是由 r1和 r2粘合得到的,若不强调 r是图 G的根,则可以简记 G=(G1,r1)∞(G2,r2);其中∞是粘合符号;显然 G的顶点集 V=(V1-{r1})∪(V2-{r2})∪{r},G的边集 E=E1∪E2。
定义 2 如果在图 T中删去所有的悬挂点及与其相关联的边后是一条路或一个孤立点,则称 T为毛毛虫树。
定义 3 如果在图 T中把所有的悬挂点及其相关联的边去掉后剩下的是毛毛虫树,则称 T为龙虾树。
2 主要结果
引理 1[3]令 (Gi,ri)是带有根 ri且存在一整和标号φi(i=1,2)的图,假设:
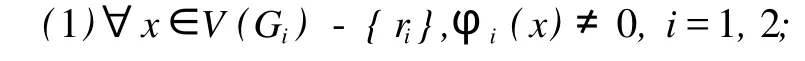
(2)φ1(x)=φ2(y)当且仅当 x=r1,y=r2;
(3)对于所有不同的 a、b∈V(G1),且 x∈V(G2)-{r2},有φ1(a)±φ2(b)≠φ2(x);
(4)对于所有不同的 x、y∈V(G2)且 a∈V(G1)-{r1},有φ2(x)±φ2(y)≠φ1(a);
则 G=(G1,r1)∞(G2,r2)是整和图。
引理 2[4]令 (G1,r1)是一个毛毛虫树,其中 r1是它的颈或头;令 (G2,r2)是一个带有根 r2的连通图,且图 G2存在一整和标号Φ,如果满足:
(1)对每一个 x∈V(G2),有Φ(x)≠0;
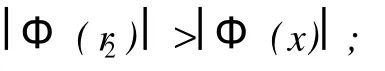
定理 1T′是毛毛虫树,在 T′的头部顶点、颈部顶点和其他顶点处分别添加一个悬挂点得到的一类龙虾树 T是整和图。
(1)令 a2是毛毛虫树的头部顶点,在此处添加的悬挂点为 a1,毛毛虫树 T′的颈部顶点规定为 a3,在此处添加的悬挂点为 a4;
(2)对于 i=1,2,…,n-1,任意两个连续的顶点 ai和 ai+1间的距离 d(aiai+1)≤3;
(3)对于每个 k∈{1,2,…,n},由 Ak={a1,a2,…,ak}的导出子图是 T的子龙虾树;序列 V={a1,a2,…,an}可以参照图 1所示。
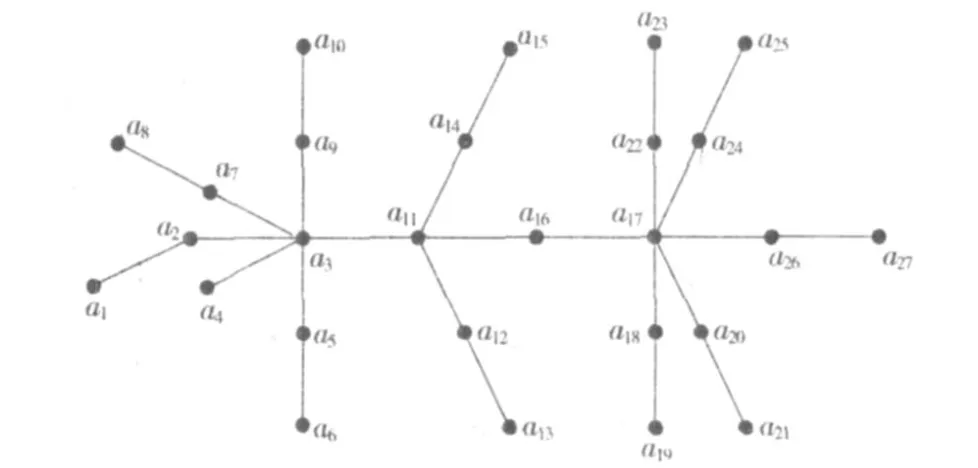
图 1 龙虾树Fig.1 Lobster tree
显然对于 i∈{2,3,…,n},存在唯一一个整数(顶点)j(i) 下面证明该标号是整和标号。φ(a1)+φ(a2)=φ(a3),φ(a2)+φ(a3)=φ(a4),φ(a3)+φ(a4)=φ(a1),从 i=5到 i=n,利用归纳法证明,n=5时,T是一棵三路树,结论成立[6];假设 n>5且结论对于n-1成立,通过归纳假设,对每个 i=6,7,…,n-1,有整和标号φ, 由引理 2可知标号φ是 T的一种整和标号,即 T是整和图。 证明 该结论直接由引理 2和定理 1可得。 推论 2有限个 (不妨设 k个)(G1,r1),(G2,r2),…,(Gk,rk)都是定理 1中的龙虾树,则 (G,r)=(G1,r1)∞(G2,r2)∞…∞(Gk,rk)也是整和图。 整和图理论研究的是图的一种标号方法,笔者以和图的理论为基础,利用顺序标号法给出一般龙虾树的一种整和标号,从而说明龙虾树的整和性质。进而用粘合的方法证明了由有限个具有一个公共顶点的龙虾树粘合而成的多重龙虾树也是整和图。该结论进一步完善了整和图理论,并为其他优美图的整和性质的研究提供了依据。 [1] MELN IKOV L S,PYATK IN A V.Regular integral sum graphs[J].DiscreteMathematics,2002,252(3):237-245. [2] CHEN ZH IBO.On integral sum graph[J].Discrete Math,2006,306(1):19-25. [3] CHEN ZHI BO.Integral sum graph from identification[J].DiscreteMathematics,1998,181(1):77-90. [4] PVATKI N A V.Subdivided trees are integral sum graphs[J].DiscreteMathematics,2008,308(9):1 749-1 750. [5] 石端银,杜 红.贝壳图是整和图[J].黑龙江科技学院学报,2008,18(6):478-479,482. [6] 路永洁.关于一类新的整和图[J].大连理工大学学报,2000,40(1):22-23. (编辑 王 冬) Research on new type of integral sum graph with method of dentification SHI Duanyin, XU Jing, CONG L ingbo O157.5 A 1671-0118(2010)05-0403-03 2010-07-06 黑龙江省教育厅科学技术研究项目(11541323) 石端银 (1980-),女,山东省菏泽人,讲师,硕士,研究方向:图论,E-mail:shiduanyin@yahoo.com.cn。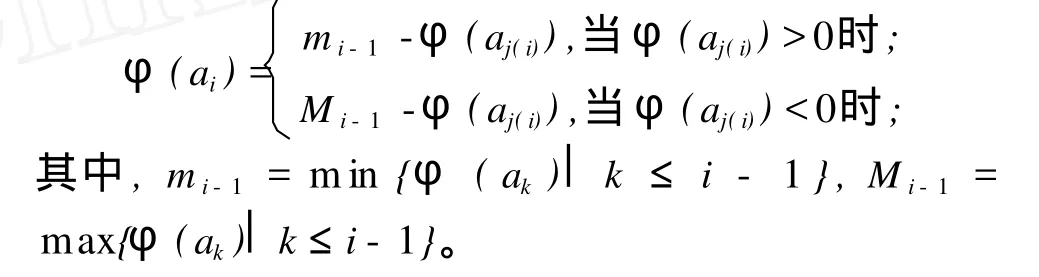
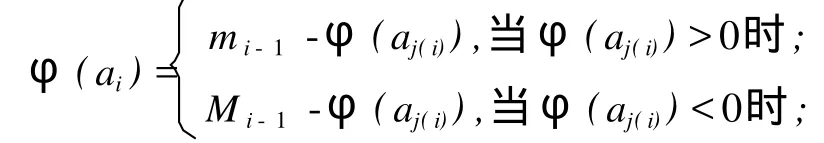



3 结束语
(College of Sciences,Heilongjiang Institute of Science&Technology,Harbin 150027,China)

