双事件触发下非匹配干扰系统积分滑模抗干扰跟踪控制

周 鹏 ,裔 扬†,朱广宇 ,王 芹

(1.扬州大学信息工程学院,江苏扬州 225127;2.北京交通大学北京市城市交通信息智能感知与服务工程技术研究中心,北京 100044)

1 引言

众所周知,未知干扰严重影响着被控系统的动态性能.如何在外部干扰的影响下,实现简单有效的抗干扰控制一直都是控制理论领域研究的热点问题[1–2].近几十年来,已经出现了许多经典的抗干扰控制方法,例如:H∞鲁棒控制理论[3]、输出调节控制[4]以及自适应控制[5]等.其中,作为一种典型的主动抗干扰方法,基于干扰观测器的控制(disturbance-observer-based control,DOBC)具有相应速度快和易于实现等优点,已经广泛应用到许多理论和实际系统中,比较典型的包括多智能系统、马尔科夫跳变系统、随机分布系统以及航天器系统等[6–9],并均取得了令人满意的抗干扰性能.在已有的研究中,相比较匹配干扰系统(即控制和控制在同一通道),实现不匹配干扰系统的干扰补偿控制将更为复杂[10];另一方面,在DOBC理论研究框架下,干扰估值的引入势必给控制端口带来更多的数据冗余和传输压力等问题.因此,研究具有较低数据传输和计算量的抗干扰算法相当迫切.

通常,数据信号的传输采用时间触发方式,即按照固定周期进行信号传输.而事件触发作为一种新的采样方式倍受关注[11–12].事件触发根据合理事件来控制数据的传输,只有在不满足事件的情况时才会更新数据,否则满足上一事件的变量将被使用.相比较周期性传输,事件触发能够明显降低信息冗余和带宽浪费[13].近年来,事件触发控制(event-triggered control,ETC)方法已经成功应用于许多控制系统中,例如:随机系统、切换系统、信息物理系统和电力控制系统等[14–17].然而,大多已有成果都是基于单一事件的触发方式.当有多个触发事件同时存在时,如何设计保证被控系统同步性和稳定性的多触发控制方式值得进一步关注.

一直以来,滑模控制(sliding mode control,SMC)因为其在不确定模型时的强鲁棒性以及能有效抑制外部干扰而受到广泛应用[18–19].其基本思路是设计合适的滑模控制器使状态变量的轨迹由外部运动至预设的滑模面,而后从滑模面向平衡点运动并在平衡点区域附近稳定[20–21].但是,传统的滑模控制器使被控系统向滑模面运动时比较敏感,容易受外部干扰或不确定性偏离轨迹.而积分滑模控制(integral SMC,ISMC)的提出能很好的消除传统滑模控制带来的影响[22–23].其中,文献[22]提出输出ISMC方法实现非线性系统的干扰抑制;文献[23]基于ISMC方法,研究车辆跟随系统的主动抗干扰控制策略.

基于以上分析,本文提出双事件触发控制模式,进而研究基于积分滑模的不匹配干扰系统抗干扰跟踪控制问题.具体的结构如图1所示.论文的主要贡献总结如下: 1)比较已有的DOBC 理论以及单触发方式,论文基于反馈状态和干扰估计值,设计“先到同触发”的双事件触发方式,明显降低输入端的数据传输和带宽浪费,同时,保证被控系统良好的同步性和动态性能;2)基于DOBC理论方法,设计积分滑模面和积分滑模抗干扰触发控制器,实现对不匹配干扰系统的干扰估计和补偿;3)通过设计的凸优化算法,计算控制器和观测器增益,保证增广闭环系统获得满意的多目标性能,包括稳定性、动态跟踪、干扰估计以及无Zeno现象.

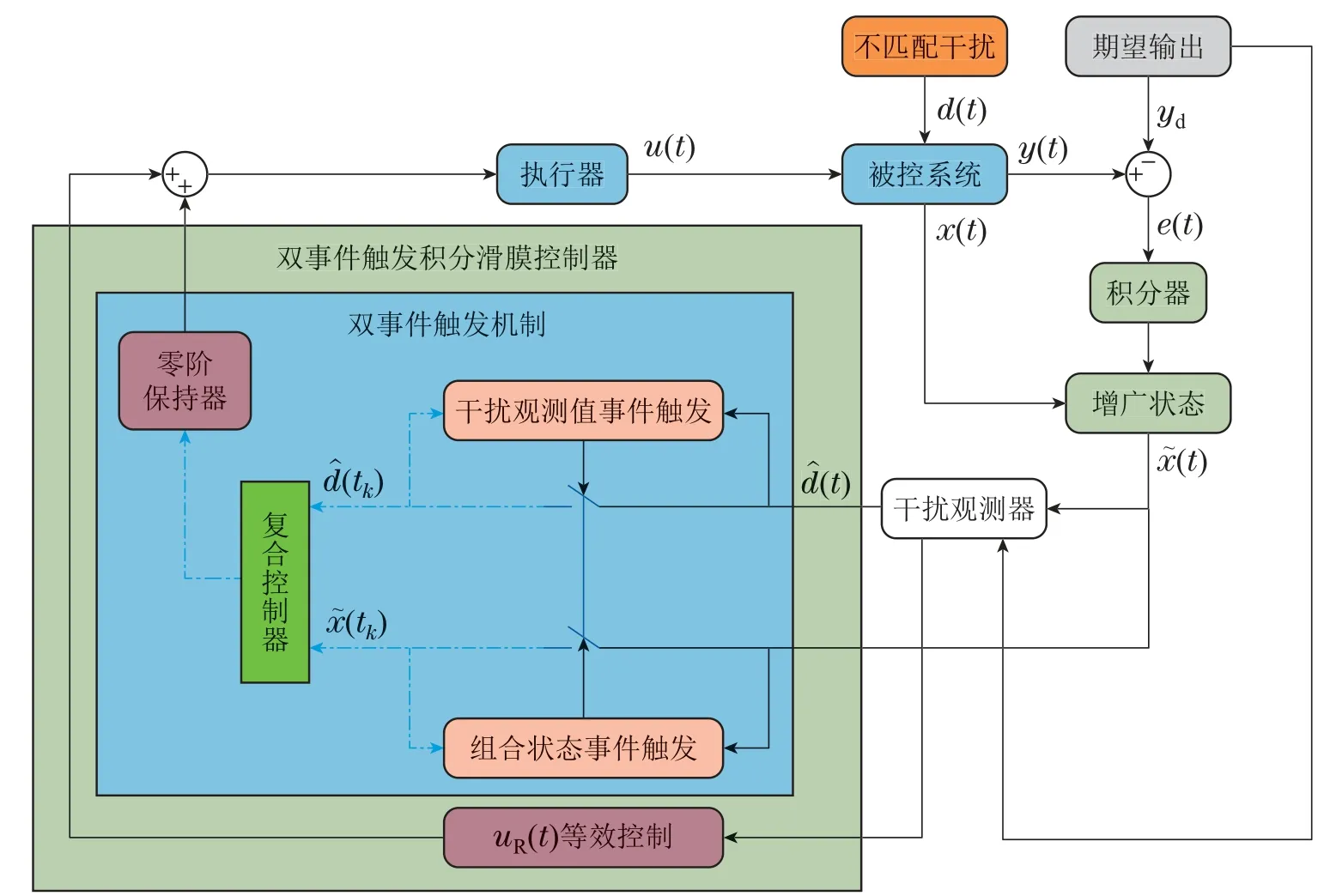
图1 双触发滑模抗干扰控制流程图Fig.1 Flow chart of double event-triggered sliding mode anti-disturbance control

本文主要数学符号定义如下: Rn表示n维实向量空间.给定一个矩阵M,sym(M)=M+MT.λmax(M)和λmin(M)分别表示矩阵M的最大/最小特征根.M+是M的左逆阵.对于任意向量函数x(t),

2 系统描述

考虑如下带有不匹配干扰的多输入多输出系统:

式中:x(t)∈Rn和u(t)∈Rm分别表示系统状态和控制输入;y(t)∈Rp是系统输出;A0,B0,C0和D0是带有适合维度的系统矩阵;d(t)表示未知外部干扰,可以用如下外延系统描述:

式中:w(t)是中间变量;W和V是相应的系数矩阵.

为了实现良好的动态跟踪,系统的状态扩展为

其中: 跟踪误差定义为e(t):=y(t)-yd;yd是期望输出向量.

注1值得注意的是,已有结果大多关注被控系统的稳定性,而对系统输出的动态跟踪性能鲜有研究.基于此,论文引入跟踪误差的动态积分项,将系统状态进行扩展,其目的是保证被控系统稳定性的同时,系统输出能够跟踪到所预设的输出向量.

基于式(1)―(3),增广系统表示如下:

为了保证算法的可行性,需要满足如下假设条件.

假设1假设未知干扰d(t)范数有界,且满足不等式‖d(t)‖<ξ,其中ξ是一个已知的正常数.

3 干扰观测器设计及性能分析

基于干扰外延模型(2)和增广系统(3),构建如下干扰观测器:

定义干扰估计误差ew(t):=w(t)-(t),得到

以下定理分析了干扰动态估计的性能.

定理1如果存在矩阵P2>0和R2,满足以下不等式:

式中α2>0是设计的正常数.则可以证明干扰估计误差系统(6)是渐进稳定的.其中,干扰观测增益L通过计算得出.

证设计相应的Lyapunov函数如下:

通过对式(8)求导并且结合估计误差模型(6),能够推导出

如果不等式(7)成立,可以得到

由此证明了干扰观测误差ew(t)渐近稳定,也体现了所设计的干扰观测器具有良好的干扰估计性能.证毕.

4 双事件触发机制

从图1可以看出,在控制端口,除了反馈状态信息,还有动态干扰估计值.为了提高传输效率并减少控制器的传输压力,引入事件触发机制来减少数据的发送量.为了确保控制稳定性和同步性,构建双事件触发机制来代替单一的单变量触发.一方面,对于增广状态(t),设计如下触发条件来决定数据的更新:

其中:σ1∈(0,1)是给定正常数,Ψ1是正定对称触发阵,且有

根据触发性质,可以推导出

5 积分滑模双触发抗干扰控制器设计

为了对不匹配干扰动态补偿,设计积分滑模面

假设2假设扰动估计误差ew(t)有界,且‖ew(t)‖≤κ,其中κ是已知正常数.

进一步,将积分型滑模控制器设计为

其中uR(t)是确保状态轨迹进入滑模面的不连续控制律,具体形式表示为

其中τR是设计的正常数.

根据式(4)(15)(18),可以推断出

以下定理给出系统状态进入预设滑模面的具体证明过程.

定理2考虑增广系统(4),在积分型滑模控制器(17)的作用下,动态轨迹最终收敛到滑模面(15).

证设计Lyapunov函数如下:

基于式(19),对式(20)求导,推导出

式中ed(t)=d(t)-(t).进而等效控制器表示为

将式(23)代入增广系统(4),得到如下闭环系统:

将干扰误差动态(6)和闭环系统(24)相结合,可以得到如下复合系统:

6 多目标性能分析

在本章节,给出相关定理验证被控系统的多目标性能.定理3证明了被控系统的稳定性,并且给出求解增益和L的具体方案.定理4给出保证动态跟踪性能的具体分析过程.定理5阐述如何避免Zeno现象.

定理3对于给定的常数0<σ1,σ2<1,σ3>0,b>0,a,µ1,µ2,α1和α2,如果存在矩阵Q1=>0,P2>0,R1和R2,保证如下不等式:

和约束条件

可解,则可证明复合系统(25)最终一致有界,且状态X(t)收敛到紧集ΥX,其中

对式(29)求导,可以得到

根据假设2,有

其中σ4=2λmin(Ψ2).另外,不难得到

基于式(30)–(33),可以推导出

非线性项-Q1Ψ1Q1可等价为

在式(26)两边同乘diag{P1,I,P1,I,I},根据Schur补理论,有

进一步,不等式(34)变换为

定理4对于给定的参数σi,i=1,2,3,4,αi,µi,i=1,2,a和b,如果存在矩阵Q1=>0,P2>0,R1和R2满足式(26)–(27)以及不等式

证对于系统输出y(t),有

其中yi(t)是y(t)的第i个分量.

基于不等式(39),可以得到

根据式(40)–(41),推导出

注2本文所设计的控制输入结构简单,由反馈状态和干扰观测两部分组成,其中控制器增益和观测器增益均可以通过求解LMI计算得到.值得注意的是,定理3和定理4中设计的不等式均为传统形式,可解参数的数量也相对有限.通过选择合适的参数,不难得到矩阵不等式的可行解,进而求出控制器增益和干扰观测器增益,并保证被控系统的性能.综上,本文所设计算法的复杂性是容易实现的.

下面定理将继续讨论事件触发机制中可能存在的Zeno现象.

定理5对于增广系统(4),在双事件触发的机制下,最小触发时间间隔的下界可以表示为

以及

可以得到相邻两次触发的间隔一定是一个大于零的正数.所以,Zeno现象将不会发生.

证定理分两种情况讨论.情况1是状态先行触发的情况,而情况2则是干扰估值先触发的情形.当这两种情况的最小触发间隔都大于零时,则可以推断Zeno现象必然不会发生.

情况1基于触发条件(11),可以得到

根据式(12),有

与式(31)相似,存在如下不等式:

因此,式(48)简化为

情况2基于干扰估值值触发条件(7),可得

根据触发的性质,可以推导出

同理,可以得到

相似于情况1,证明干扰估值事件触发最小间隔为

综合情况1和情况2,无论哪个变量先触发,触发的最小间隔总是大于0.所以,闭环系统(4)可以避免Zeno现象.证毕.

7 数值仿真

考虑如下A4D无人机系统模型:

相关参数选择如下:

不匹配干扰模型(2)中的参数选择为

设计可调参数µ1=0.2,µ2=0.3,α1=0.01 和α2=0.02 以及触发参数σ1=0.0027,σ2=0.002,σ3=0.005,a=1.1和b=0.1.此外,触发矩阵Ψ1和Ψ2取为合适维度的单位矩阵.求解定理3中的矩阵不等式,计算出

选择初始值x(0)=[-22-2.3 1-2]T,期望输出yd=20.控制系统的状态反应曲线如图2所示.图3是系统的输出轨迹.不匹配干扰d(t)和触发更新值(tk)的比较分析如图4所示.图5是双触发的时间和间隔.从仿真结果可以看出,本文所设计的算法能够完成对干扰的估计和补偿,进而保证了被控系统满意的稳定性和动态跟踪性能.

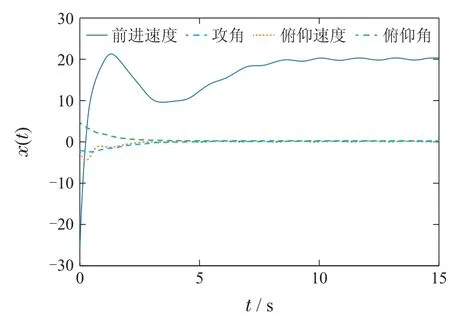
图2 系统状态反应曲线Fig.2 The response curves of system state

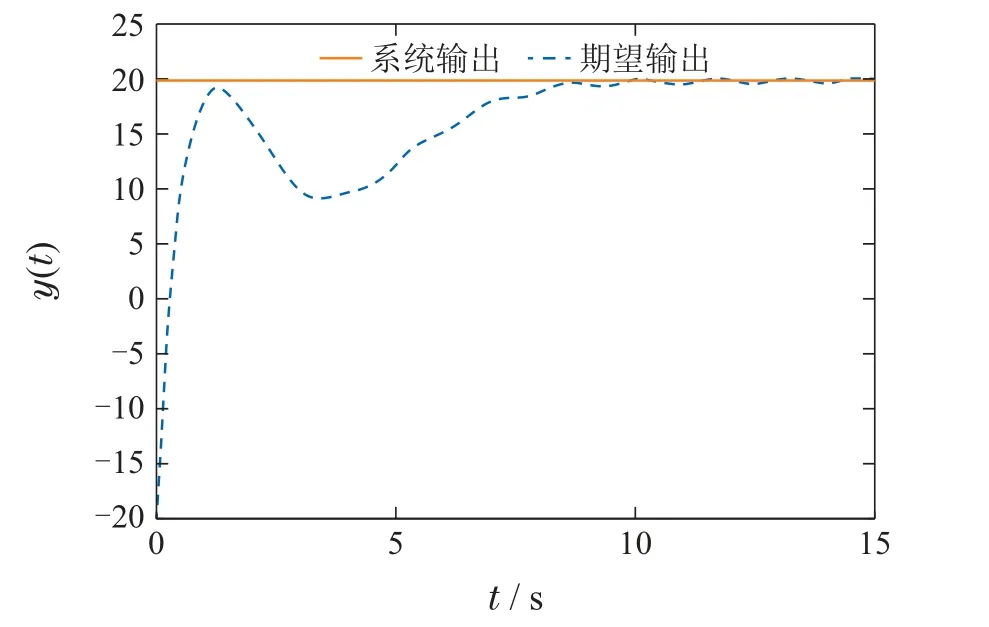
图3 系统动态输出Fig.3 The dynamic outputs of system

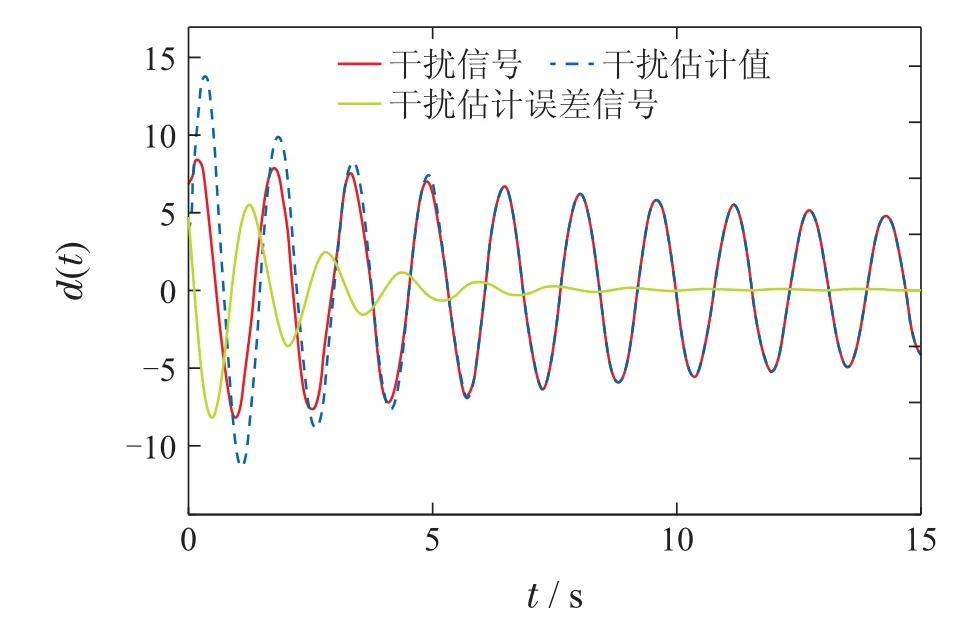
图4 干扰和干扰估计值Fig.4 Disturbance and its estimation

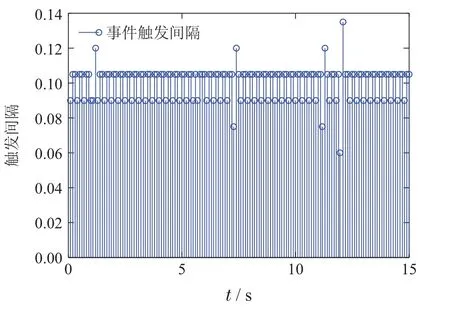
图5 事件触发间隔和更新Fig.5 Events-triggered intervals and updates

8 结论

本文研究了多事件触发条件下非线性系统积分滑模抗干扰控制问题.相比较单触发问题,双触发的设计能够进一步减少传输数据,而“先到同触发”的机制则能在节约资源的同时保证被控系统的同步性和稳定性.为了降低不匹配干扰的影响,基于DOBC方法,设计积分滑模面和积分滑模抗干扰控制器,实现对未知不匹配干扰的估计和补偿.通过Lyapunov分析法,计算控制器和观测器增益,验证了被控系统获得满意的稳定性和动态跟踪性能.进一步,通过求解多触发的最小间隔证明了Zeno 现象不会发生.最后,基于A4D模型的仿真结果表明了设计算法的可行性.