基于BAS-PSO的半主动悬架自抗扰控制
张前满, 汪志锋, 徐 洁
(上海第二工业大学 智能制造与控制工程学院,上海 201209)
汽车悬架系统是汽车工业中不可或缺的重要组成部分。悬架系统通过吸收和缓和路面不平对车体的冲击从而提升汽车的乘坐舒适性和稳定性[1-2]。然而,传统的被动悬架由于刚度和阻尼的不变性,无法根据实际路面情况进行实时调节,因此减振效果较差。相比之下,半主动悬架则能够根据路面扰动实时进行阻尼调节,并且相对于主动悬架[3],其成本更低,控制更为简单,因此在实际生活中得到广泛关注和应用。目前,半主动悬架的优化研究已经成为学术界的热点之一[4]。
自抗扰控制(Active Disturbance Rejection Control,ADRC)技术由中国科学院数学所韩京清教授于1998年正式提出[5]。ADRC发扬传统PID控制的精髓,并结合现代控制理论成就,成为一种不依赖于被控对象精确模型的新型实用数字控制技术[6]。相比其他控制技术,ADRC能够主动从被控对象的输入输出信号中提取扰动信息进行消除,从而极大地降低扰动对于被控量的影响,做到“防范于未然”[7],具有很高的鲁棒性和自适应性[8]。然而,由于ADRC需要调整的控制参数较多,人工整定过程较为烦琐和困难,因此,需要探索更优的自适应寻优算法,以提高ADRC的性能和应用范围[9-11]。
粒子群优化(Particle Swarm Optimization,PSO)算法最早是由Kennedy和Eberhart于1995年提出的,是一种启发式寻优算法[12],该算法基于群体智能的思想,模拟粒子在解空间中的搜索过程,能够快速找到最优解。然而,传统PSO算法在应用过程中存在易陷入局部最优和后期多样性差等问题[13-15]。
本文以二自由度1/4半主动悬架作为研究对象,利用ADRC技术实现对于汽车半主动悬架的控制。为解决自抗扰控制器参数需人工试取整定和整定难度大的问题,提出了一种基于天牛须粒子群优化BAS-PSO的在线整定方法。该方法通过在传统PSO算法的基础上加入BAS算法,能够有效克服PSO算法后期陷入局部最优和多样性变差的缺点。通过仿真验证,表明了BAS-PSO粒子群算法的优胜性以及通过算法寻优后自抗扰参数的有效性和优越性。
1 模型建立
1.1 二自由度1/4车辆半主动悬架模型
二自由度1/4半主动车辆悬架模型能较好地反映汽车的垂向振动特性,且易获取车身垂直方向加速度、悬架动挠度和轮胎动载荷等性能指标。半主动悬架系统模型及根据牛顿第二定律得出的运动微分方程如式(1)所示,示意图如图1所示。

图1 1/4半主动车辆悬架模型示意图
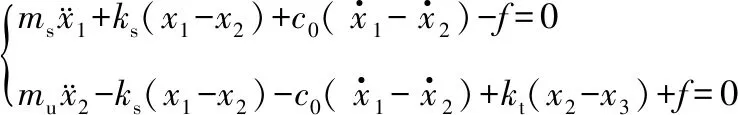
(1)
式中:ms、mu分别为簧载质量和非簧载质量;ks为悬架弹簧刚度;kt为轮胎刚度;c0为阻尼系数;f为悬架可调阻尼力;x1、x2、x3分别为簧载位移,非簧载位移以及路面扰动输入。
在MATLAB/Simulink环境下搭建1/4悬架Simulink模型,如图2所示。
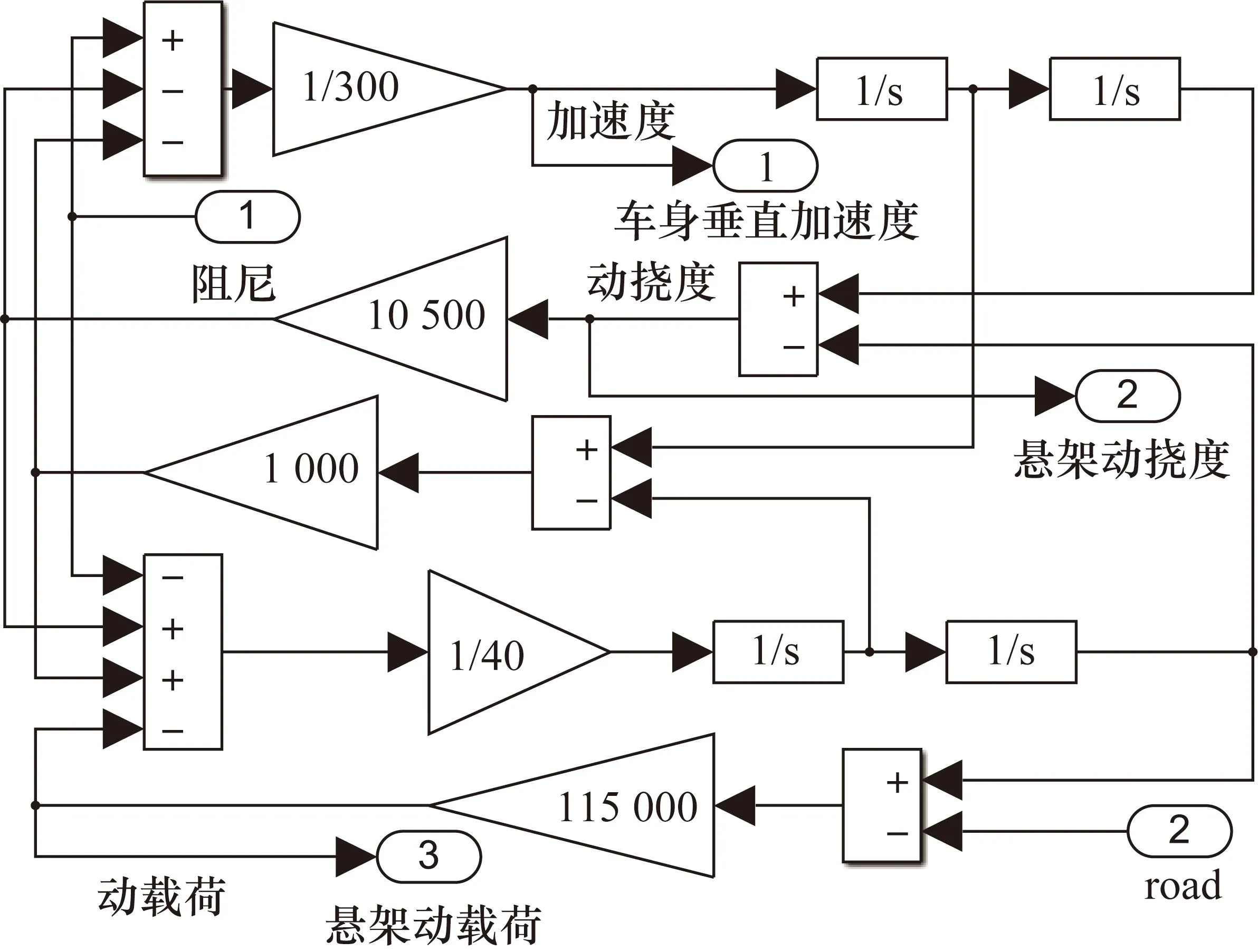
图2 1/4半主动悬架Simulink模型
所采用的车辆结构参数如表1所示。

表1 车辆悬架结构参数
1.2 系统稳定性分析
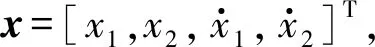
(2)
其中:
C=[1 0 0 0],D=[0 0]
(3)
根据表1模型参数带入式(3)后,通过MATLAB对于能控型矩阵M=[B,AB,A2B,A3B]和能观性矩阵N=[C,CA,CA2,CA3]T分别进行秩的计算得出rank(M)=rank(N)=4,故该系统能控且能观。
根据半主动悬架系统的状态空间方程,对于系统进行稳定性分析。图3分别给出了系统的闭环根分布情况、奈奎斯特稳定性分析图以及系统在单位阶跃下的响应曲线。
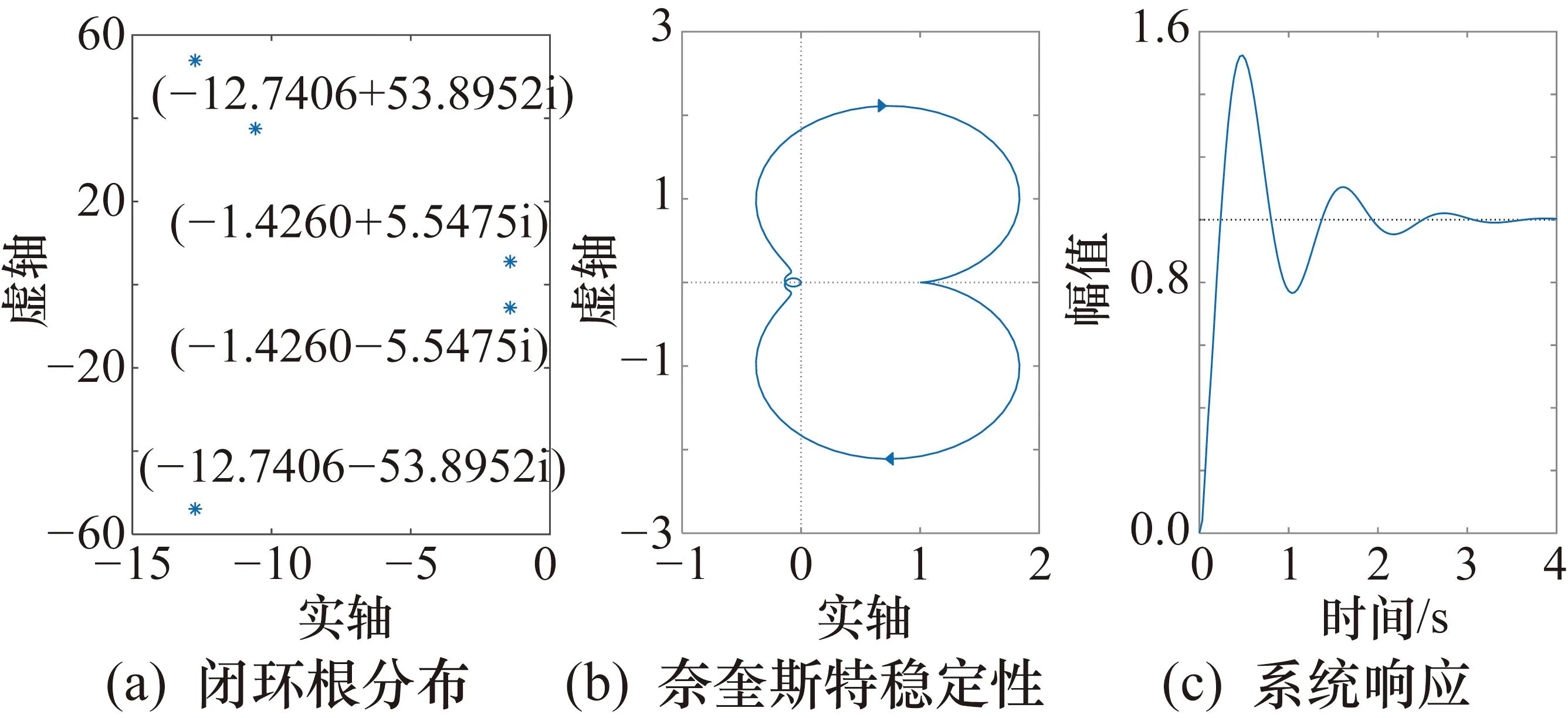
图3 稳定性分析曲线
由图3可知,半主动悬架系统闭环极点均具有负实部;奈奎斯特幅频特性曲线不包围复平面的(-1,j0)点且系统在受到单位阶跃信号时,能够趋于平稳并稳定在单位阶跃的振幅上,故该闭环系统稳定。
1.3 路面激励模型
路面激励是悬架系统中不可忽视的因素,它对汽车的行驶稳定性和乘坐舒适性有很大影响,本文采用基于滤波白噪声路面激励模型[16],时域描述为
(4)
式中:nq为下截止频率;x(t)为路面激励;n0为空间频率;Gq(n0)为路面不平度系数;w(t)为单位白噪声。图4展示了基于滤波白噪声的路面模型结构,图5为车速20 km/h时B级路面的时域信号。

图4 滤波白噪声路面模型

图5 B级路面时域信号
2 ADRC设计
ADRC主要由跟踪微分器(Tracking Differentiator,TD)、非线性状态误差反馈(Nonlinear States Error Feedback,NLSEF)和扩张状态观测器(Extemded State Observer,ESO)三部分组成[17]。TD通过安排过渡过程,对目标值进行平滑处理,以解决快速性和超调之间的矛盾;NLSEF继承了传统PID控制的“以误差消误差”的思想,通过非线性组合取代了线性加权,同时利用扩张状态观测器的误差观测结果对非线性组合进行修正;ESO将被控系统的所有不确定因素归结为“未知扰动”,通过控制量输入和系统实际输出对其进行估计,从而进行扰动补偿,做到主动抗干扰[18]。ADRC具有很强的适应性和鲁棒性,并已广泛应用于工业控制、机器人控制和动力学系统等领域。半主动悬架的ADRC基本结构图如图6所示。
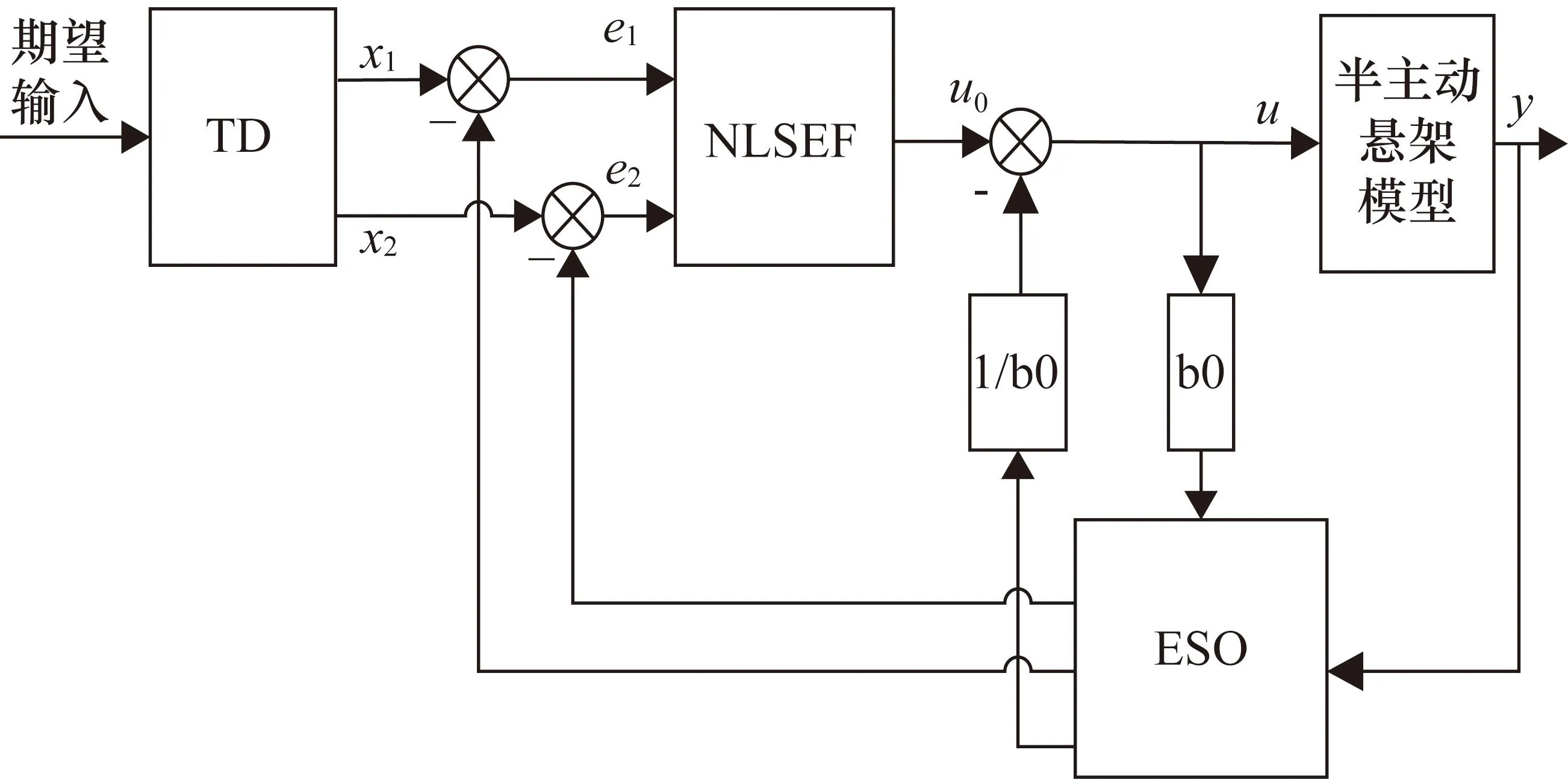
图6 ADRC结构
2.1 TD
TD离散形式如下:
(5)
式中:v(k)为二自由度1/4半主动悬架车身加速度的参考输入,为了使车身在扰动作用下保持在平衡位置,本文取v(k)=0;r0和h0分别为速度因子和滤波因子,实现对于信号的快速跟踪和滤波;h为系统采样时间,本文取h=0.01。TD采用最优快速综合函数fhan(·),以安排信号的过渡过程,避免产生超调,该函数表达式如下:
(6)
2.2 NLSEF控制律
NLSEF定义e1、z1为车身跟踪加速度误差和车身观测加速度;e2、z2为车身跟踪加速度微分值误差和车身观测加速度微分值,其非线性控制方程如下:
(7)
式中:
(8)
式中:a1,a2为非线性因子;β1,β2为函数增益;fal(·)为非线性函数。当a<1时,非线性函数具有“大误差,小增益;小误差,大增益”的特性。u0为半主动悬架的阻尼的反馈控制力输入。
2.3 ESO
ESO通过将路面激励等外部扰动和系统未建模误差内部扰动视为系统的“总未知扰动”,并进行补偿。其数学表达式如下:
(9)
式中:y为车身加速度的实际值输出;z1为系统输出观测值;z2为系统输出微分观测值;z3为系统总扰动观测值;β为ESO的增益系数;α为非线性因子;b为放大系数。通常取α1=0.5,α2=0.25。
3 BAS-PSO自抗扰参数优化
3.1 标准PSO算法原理
PSO算法是一种模拟鸟群觅食行为的优化算法,其将鸟群中的个体视为粒子,在解空间中以鸟群觅食飞行逻辑搜索最优解。PSO算法通过不断更新粒子位置和速度来寻找最优解。其粒子速度和位置更新公式如下:
(10)
(11)
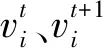
3.2 BAS-PSO算法融合
BAS算法具有运算速度快、结构简单的优点。天牛粒子通过天牛触角判断左右食物浓度,并向浓度较大一侧移动[19]。BAS-PSO算法集合了BAS的搜索速度及PSO的精细搜索能力,能够有效解决粒子群后期多样性差和易局部最优问题。结合算法更新规则如下:
(12)
dt=0.95×dt-1
(13)
(14)
(15)
(16)

(17)
(18)
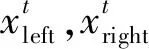
3.3 算法步骤流程
BAS-PSO算法的寻优过程主要可分为以下6个步骤。具体如图7所示。

图7 BAS-PSO算法流程
① 粒子初始化。
设置初始粒子群大小和维度、最大迭代次数以及位置和速度限制等参数。
② 产生初始粒子群。
初始化完成,计算粒子适应度,以当前粒子位置为个体最佳位置gbest,以最小适应度位置为群体最优zbest。
③ 设置迭代。
将每个粒子作为天牛群个体的质心,按照式(12)计算天牛群的左右须触角位置,并计算左右适应度f(xleft)和f(xright)。
④ 位置更新。
根据式(16)对粒子位置进行更新,重新计算适应度,若适应度值f ⑤ 适应度计算。 将新的zbest、gbest代入式(17)、式(18)得到粒子群搜寻速度和新位置,计算适应度并更新。 ⑥ 判断是否达到最大迭代次数。 判断是否达到最大迭代次数,是则返回最优值zbest及其适应度,否则返回步骤③。 BAS-PSO主要针对自抗扰NLSEF和ESO的β1、β2、β01、β02、β03这5个参数进行整定,其中,NLSEF和ESO是控制系统中最为重要的部分,需要精确调整这5个参数才能获得良好的控制效果。为求解NLSEF和ESO的5个参数最优值,以半主动悬架的车身加速度、悬架动挠度、轮胎动载荷性能指标均方根值的和作为适应度函数[20],通过不断迭代和更新粒子的位置和速度来寻找最优解。在迭代过程中,BAS-PSO算法结合了BAS算法的搜索速度和全局搜索能力以及PSO算法的精细搜索能力,并利用BAS算法来帮助粒子群摆脱局部最优解,其算法结构如图8所示。 图8 算法结构 适应度函数: (19) 根据上述内容,在Simulink中搭建的总仿真系统模型如图9所示。 试验中,ADRC其他相关参数如表2所示。 表2 自抗扰参数表 根据二自由度1/4半主动悬架的适应度收敛曲线进行BAS-PSO算法和标准PSO算法对比分析,结果如图10所示。 图10 适应度收敛曲线比较 由图10可以明显看出,标准PSO算法在迭代过程中,由于粒子的多样性下降,最终在第30代左右陷入局部最优解。相比之下,BAS-PSO算法通过不断获取天牛左右须的浓度,进行位置更新,可以较好地维持粒子的多样性,避免算法过早陷入局部最优解,从而具有更好的全局搜索能力。此外,BAS-PSO算法在初期搜索效率上也明显优于标准PSO算法,能够更快地找到较优解。综合对比表明,BAS-PSO算法相对于标准PSO算法具有更优越的性能和更高的实用性。 对BAS-PSO参数寻优的ADRC与被动悬架、粒子群PID控制、粒子群ADRC的试验结果进行分析,系统仿真结果如图11~图13所示,经过BAS-PSO参数寻优后自抗扰半主动悬架与其他算法性能指标均方根值对比如表3所示。 表3 性能指标对比(均方根) 图11 车身加速度控制效果对比 图12 悬架动挠度控制效果对比 图13 轮胎动载荷控制效果对比 由图11~图13和表3数据可以得出:BAS-PSO-ADRC半主动悬架在各项性能指标上均优于被动悬架、PSO-ADRC控制、PSO-PID控制。具体来说,车身垂向加速度BAS-PSO-ADRC相对于被动悬架、PSO-ADRC控制、PSO-PID控制分别优化了50.92%、9.76%、41.46%;悬架动挠度分别优化了26.72%、13.96%、26.75%;轮胎动载荷分别优化了16.12%、1.31%、8.02%。因此,采用BAS-PSO-ADRC半主动悬架控制方法可以有效提高车辆行驶过程中的平稳性、舒适性和安全性,具有更高的实用性和可靠性。 在已有的半主动悬架模型基础上,通过设计自抗扰控制器,成功实现了对半主动悬架的减振控制。采用BAS-PSO算法,通过融合BAS算法和PSO算法,增强了粒子多样性并避免了粒子群局部最优问题。通过BAS-PSO算法实现了对自扰控制器参数的优化,并与其他控制算法进行对比分析,验证了算法的可行性和优越性。3.4 自抗扰参数寻优

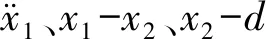
4 仿真结果与分析

4.1 算法比较分析

4.2 悬架系统时域仿真结果分析
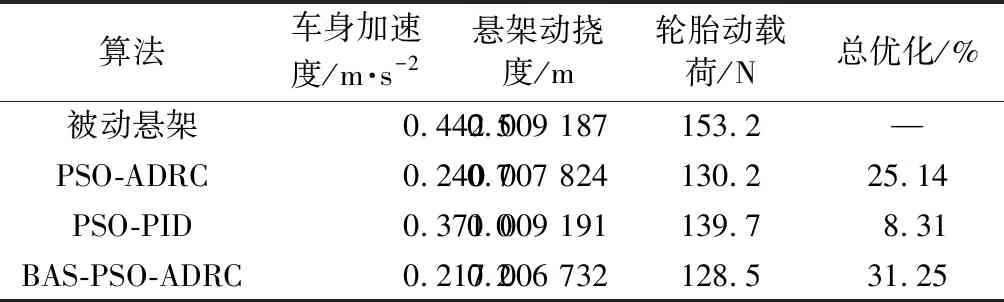

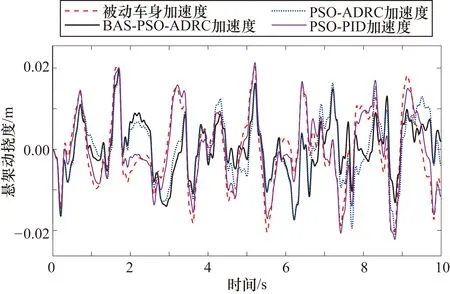

5 结束语

