固定翼无人机集群分布式固定时间编队跟踪控制

田 霖, 孙 亮

(1.民政部一零一研究所,北京 100070; 2.北京科技大学 智能科学与技术学院,北京 100083)

近年来,随着控制理论、导航技术、材料科学的发展,无人机技术得到了较快发展,无人机也在应急救援、农林植保、电力巡线等民用领域以及侦察、干扰、打击等军事领域得到了越来越广泛的应用。随着无人机技术研究的深入,无人机呈现出了成本高、研制周期长、系统复杂等特点,严重限制了其在更广泛领域和场景的应用。针对这些特点,无人机集群概念应运而生,其通过多架低成本小型无人机相互协同配合完成任务,可以解决单架无人机鲁棒性、容错性差等问题,同时降低了无人机研制成本,缩短了研制周期,因此受到了各国研究人员的广泛关注[1-4]。

编队跟踪控制问题是无人机集群领域的一类重要问题,主要控制方法包括一致性方法和领航跟随法。文献[5]考虑了无人机的外部扰动和状态受限问题,利用一致性方法解决了多架无人机编队跟踪控制问题。文献[6]基于领航跟随架构设计了无人机集群的分布式自适应有限时间控制算法,实现了在扰动条件下集群的协同编队跟踪控制。针对无人机集群编队重构问题,文献[7]基于自适应终端滑模和干扰观测器设计了分布式编队跟踪控制器,实现了有限时间编队跟踪控制。文献[6]和文献[7]都实现了有限时间编队控制,但是收敛时间上限均与系统初始状态相关,如果系统初始状态距离平衡点较远,那么收敛时间就会很长,严重限制了其在工程中的应用。例如,集群发现障碍物需要紧急变换阵型进行避障,那么集群必须在碰撞障碍物前的规定时间内完成阵型变换,因此其完成任务的时间有固定上限。为了解决这个问题,文献[8]提出了固定时间概念,明确了系统收敛时间与初始状态无关而只与设计参数相关。基于固定时间概念,文献[9]利用终端滑模方法解决了一类非线性系统的固定时间镇定问题。文献[10]和文献[11]在文献[9]的基础上将终端滑模方法推广到多智能体系统中,针对一阶积分器多智能体系统设计了非线性一致性控制律,实现了系统的固定时间一致性。文献[12]设计了一致性控制律,解决了二阶积分器多智能体系统的固定时间一致性问题。针对由多个谐波振荡器组成的多智能体系统,文献[13]利用非奇异固定时间终端滑模设计了非线性控制律,实现了多智能体对领航者的一致性跟踪。针对高阶积分器多智能体系统,文献[14]基于领航跟随架构设计了固定时间一致性控制器,将固定时间滑模方法扩展到了高阶积分器多智能体系统上,解决了任意阶多智能体系统的固定时间一致性问题。以上研究只集中在由积分器模型组成的多智能体系统的固定时间一致性问题上,而针对无人机集群的固定时间编队跟踪控制问题目前还没有研究成果,因此本文针对该问题进行了研究。

本文针对带有执行器未建模动态和不确定性的无人机集群系统,利用非奇异固定时间终端滑模方法,设计了集群编队跟踪控制器,实现了集群无人机在固定时间内编队成为理想构型,且收敛时间上界与初始状态无关。最后,通过数值仿真验证了所设计控制器的有效性。

1 问题描述

考虑一组由N个无人机组成的集群系统,其在地面坐标系(东北天坐标系)下的三自由度(3DOF)质点运动模型[15]可以描述为

(1)

式中:i=1,2,…,N;xi、yi、zi分别为集群中第i个无人机在地面坐标系下的三维位置坐标;Vi、γi、χi分别为第i个无人机的地速大小、航迹方位角和航迹倾角;Vci、γci、χci分别为Vi、γi和χi相应的控制输入;τV、τχ、τγ分别为Vi、γi、χi相应的时间常数。

令pi=[xi,yi,zi]T为集群中第i个无人机的位置矢量,vi=[vxi,vyi,vzi]T为第i个无人机的速度矢量,ui=[uxi,uyi,uzi]T为第i个无人机在地面坐标系3个轴向上的控制输入矢量。同时考虑无人机执行机构的未建模动态和不确定性,则式(1)的模型可以转换为[15]

(2)

式中:di=[dxi,dyi,dzi]T为第i个无人机的执行器产生的未建模动态和不确定性矢量。由文献[15]可知,式(1)中第i个无人机的控制输入Vci、γci、χci与式(2)中控制输入矢量ui的关系可表示为

(3)

假设1:式(2)中的扰动矢量di是有界的,上界已知且满足‖di‖≤dmax,dmax为正常数。

假设2:领航者的位置pd、速度vd和速度的导数gd都是有界的,且上界已知。

假设3:理想编队构型的位置变量hpi、速度变量hvi和速度变量的导数gai都是有界的,且上界已知。

(4)

基于式(4),可以将式(2)的模型转换为编队误差系统,形式为

(5)

进一步地,定义变量e1i和e2i为

(6)

(7)

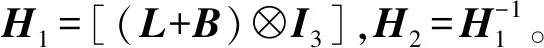
针对无人机集群固定时间编队跟踪控制问题,本文将设计跟踪误差系统中的ui,使得集群中每个无人机的跟踪误差epi和evi都在固定时间内收敛到0。

2 控制器设计

为了设计控制器,首先引入一种滑模。

引理1[16]:考虑如下滑模:

(8)

式中:x∈R为连续变量;fs(x)形式为

(9)

(10)

(11)

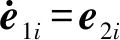
(12)

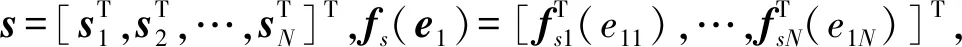
s=H1[e2+fs(e1)]

(13)

基于固定时间滑模式(式(12)),设计集群中第i个无人机的控制律为

(14)

(15)

(16)

式中:m=1,2,3;ψi=[ψi1,ψi2,ψi3]T∈R3为扰动补偿项,其形式为[17-18]

(17)

式中:m=1,2,3;ku和κi为正常数且满足κi≥dmax+‖udi‖,ζ为正常数。由文献[17]和文献[18]可知,扰动补偿项ψi满足如下关系:

(18)

在给出定理和证明之前,首先引入以下引理。

定理1:考虑无人机集群系统(式(1)),无人机间的通信拓扑为无向连通图,理想的编队位置和速度构型为hp和hv,那么针对相应的编队误差系统(式(5)),设计控制律形式如式(14),那么可以得到如下结论。

(1) 滑模s在固定时间T1内收敛到区域Ω1内。收敛时间上界T1为

(19)

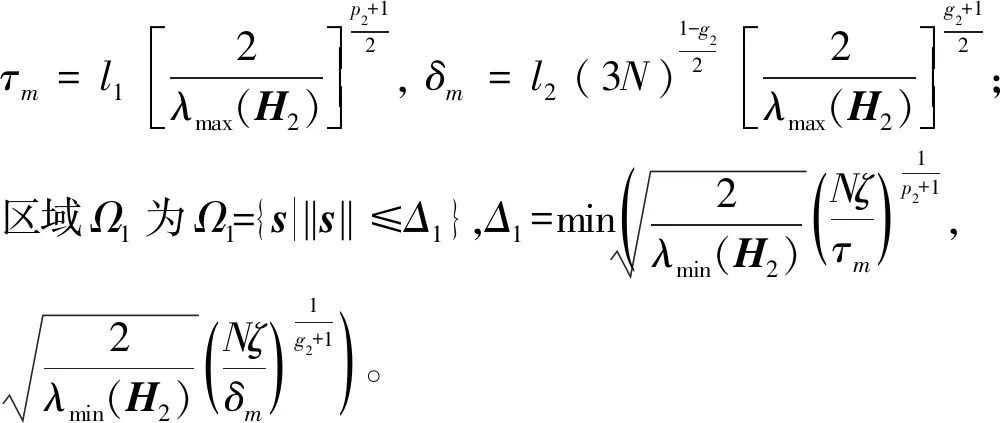
(2) 跟踪误差epi和evi在固定时间Tt内收敛到区域Ω2内。其中时间Tt=T1+T2,其中

(20)

证明:首先证明滑模到达段的收敛性,选取Lyapunov函数为

(21)

对V求导可得:

(22)

由控制律式(14)和式(18)可得:

(23)

式(23)可以表示为以下两种形式:

(24)

(25)

然后证明滑模滑动段的收敛性,基于结论(1)可以得到‖H2s‖≤‖H2‖Δ1,进一步可以得到evim+fs(epim)≤‖H2‖Δ1。利用文献[16]中的分析方法对跟踪误差epi和evi的特性进行分析可知,滑动模态s进入滑模面附近的小区域后会出现3种情况:

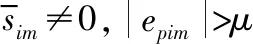
综上所述,跟踪误差epi和evi最终在固定时间Tt内收敛到区域Ω2内。结论(2)得证。

注1:控制器(式(14))实现了集群系统(式(1))的固定时间编队跟踪控制。相较于文献[7]的集群有限时间编队控制,给出了明确的收敛时间上界,该上界与初始状态无关,只与控制器参数相关,因此可以根据任务指标调整设计参数,在规定时间内完成任务,更具有工程应用价值。

注2:基于滑模(式(12))所设计的控制器(式(14))针对的模型是编队误差系统(式(7)),目的是使系统(式(7))中的变量e1和e2在固定时间内收敛到小区域内,进而根据式(7)中e1和e2与ep和ev的关系得出跟踪误差epi和evi在固定时间Tt内收敛到区域Ω2内,即集群中各无人机的速度和位置与其在编队构型中相应的理想的速度和位置的误差收敛到区域Ω2内,最终达到集群无人机在固定时间内完成理想编队构型的目的。

注3:所设计的控制器(式(14))基于滑模方法,首先证明了滑动模态在到达段的收敛性,即滑动模态在固定时间T1内可从空间任意位置到达滑模面s=0的附近小区域Ω1内。然后证明了滑动模态在到达段的收敛性,即滑动模态到达小区域Ω1后会在固定时间T2内收敛到原点附近的小区域Ω2内。因此,跟踪误差epi和evi最终在Tt内收敛到Ω2内,这意味着每个无人机的位置和速度与其在编队构型中理想位置和速度之间的误差在范围Ω2内,完成了理想的编队构型。

3 仿真验证

为了验证所提出的无人机集群分布式固定时间编队跟踪控制算法的有效性,进行如下数值仿真。考虑一组由3个无人机和1个虚拟领航者组成的集群系统,3个无人机间均可以进行双工通信。无人机模型(式(1))中的各状态变量的初始值取表1中的值,时间常数τV、τχ和τγ分别取值为3、1.5和1.5。集群中3个无人机都存在相互的机间通信,无人机2与虚拟领航者进行通信。虚拟领航者的初始位置为[0,0,100]T,速度为[22.63,22.63,0]T。编队的理想位置构型和理想速度构型分别取表1中的值。式(2)中的di=0.001×[sin(t),cos(t),-sin(t)]T。

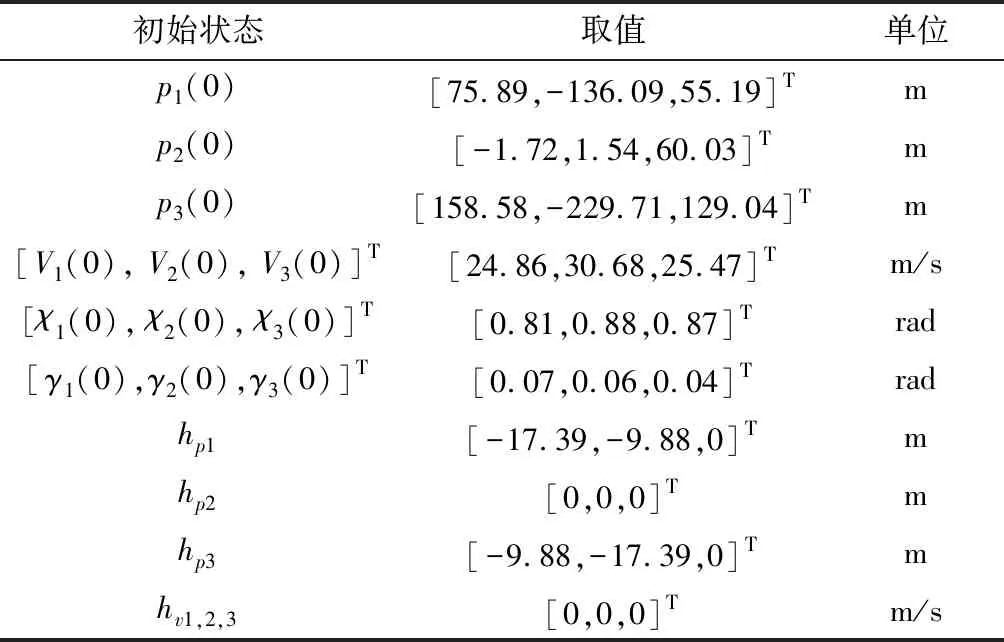
表1 编队初始状态和参数

数值仿真中控制器取式(14)的形式,式(14)中的滑模面取式(12)的形式,其中的参数选取为α1=β1=0.15,l1=l2=0.5,p1=p2=0.6,g1=g2=9/7,μ=0.1,ku=0.278 5。

数值仿真结果如图1～图6所示。

图1 集群中无人机的速度、航迹方位角和航迹倾角

图1为集群中3架无人机的速度、航迹方位角和航迹倾角的变化曲线,可以看出集群中各无人机的速度在7.5 s内与理想值保持一致,航迹方位角和航迹倾角在14 s内与理想值保持一致,说明无人机在固定时间内完成对虚拟领航者的跟踪。图2和图3分别为式(4)中定义的位置跟踪误差epi和速度跟踪误差evi的变化曲线,可以看出这2种误差均在14 s内收敛到0,说明集群中无人机在固定时间内实现了理想的编队构型。图4为3架无人机从初始时刻0 s到最终时刻100 s的三维飞行轨迹,图5为3架无人机在最终时刻的航迹俯视图。由图4和图5可以看出集群中的无人机由初始时刻的分散位置形成了最终理想的三角形编队。图6为集群的3架无人机在最终时刻形成的三角形编队阵型的俯视图。

图2 集群中无人机的位置跟踪误差

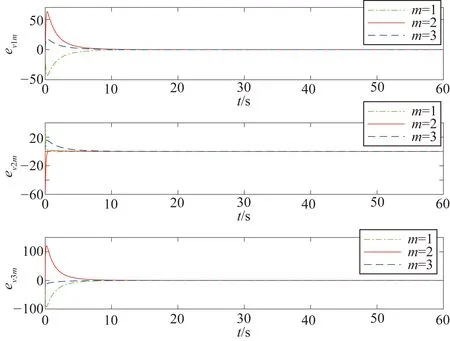
图3 集群中无人机的速度跟踪误差

图4 集群中无人机的飞行轨迹

图5 集群中无人机最终时刻的航迹(俯视图)

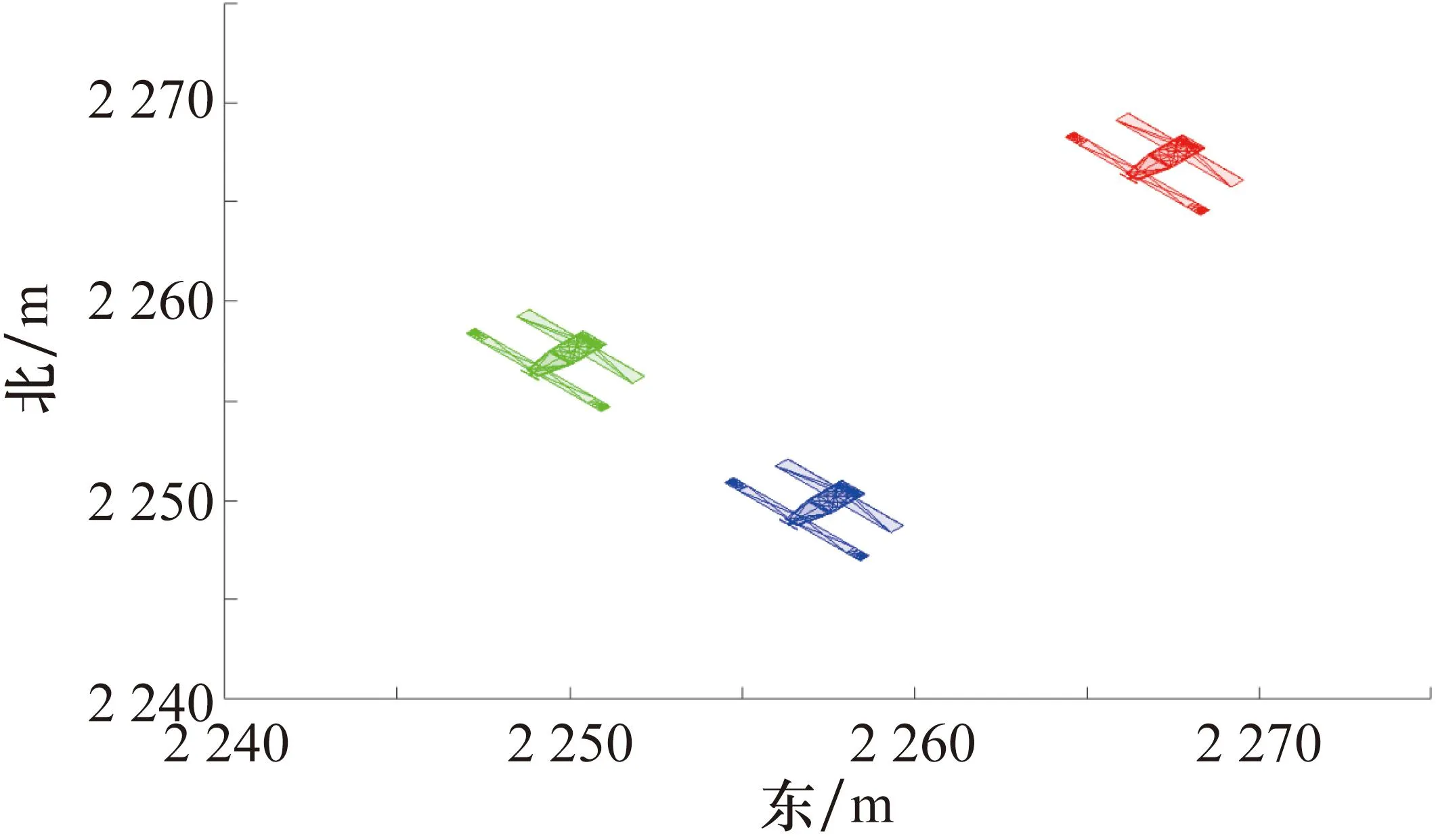
图6 集群中无人机的最终编队阵型(俯视图)

4 结束语

本文研究了无人机集群的分布式固定时间编队跟踪控制问题。针对带有执行器未建模动态和不确定性的无人机集群系统,基于收敛时间独立于初始状态的固定时间终端滑模设计了分布式编队协同跟踪控制器,实现了无人机集群在固定时间内对理想编队构型的跟踪。同时设计了补偿外部扰动的鲁棒项,增强了系统的鲁棒性。通过数值仿真,验证了所设计控制器的有效性。