通道间串扰测量不确定度评定

梁志国,冯秀娟

(1.航空工业北京长城计量测试技术研究所 计量与校准技术重点实验室,北京 100095;2.中国计量科学研究院 力学与声学计量科学研究所,北京 100029)

通道间串扰是多通道系统中的一个普遍现象[1-4],并不局限于数据采集系统,其本质上都属于表征不同通道之间的相互干扰,但由于干扰原因、干扰路径、干扰频段、干扰强度与特征,以及系统本底噪声等的不同,其测量方法也不尽相同。

通道间串扰是数据采集系统等数字化多通道测量仪器设备的一种抗干扰指标参数,是由于电路系统中储能电路元件部分的能量存储与释放,导致数据采集过程中前一采集通道会对其逻辑后继采集通道产生影响,其与共模抑制比等同属抗干扰特性参数。

尽管已经有学者研究过数据采集系统通道间串扰的测量评价[5-6],并进行了不确定度相关研究,但仍然不能完全令人满意。有众多校准人员认为其不易评定,或者不知如何评定,主要是评定结果不确定度很大,且波动很大。究其原因,主要是干扰本身幅度较小,且不够稳定,其本身属于直流还是交流不明确,干扰与系统的本底噪声以及直流偏移与干扰本身合在一起且不易分离。

通常,抗干扰参数本身的测量离散性较大,因而需要进行不确定度评定。本文主要以数据采集系统校准规范所列的通道间串扰测量方法为对象[7-9],使用剔除直流偏移的干扰幅度绝对值衡量干扰,并使用剔除直流分量的本底噪声幅度绝对值表征本底噪声,以两者之差与干扰激励幅度之比衡量串扰,进而评定测量不确定度。

1 通道间串扰测量原理与方法

通道间串扰校准接线图如图1所示,选择采集顺序上连续的2个以上通道(如w,w+1,…)作为测量通道。通道w接到直流电压源上,w+1等通道接入电阻R0。图1中R0为模拟信号源内阻的不平衡电阻,本文选为1 kΩ。通道w选取最大量程,通道w+1等其他通道均选取最小量程。同时设置采集速率和通道采集数据个数n(≥100)。

图1 通道间串扰校准接线图

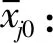
(1)

(2)

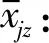
(3)

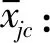
(4)

(5)

按式(6)计算通道j对通道w的串扰抑制比SSCRR,j:

(6)

式中:Gj为测量通道j的增益值,系统的通道间串扰抑制比由SSCRR,w+1给出。

2 测量不确定度模型

为获得通道间串扰抑制比的测量不确定度模型,对其测量模型式(6)微分可得:

(7)

式中:c1～c4为灵敏系数[10],即

(8)

(9)

(10)

(11)

假设各个不确定度分量互不相关,因此可得到通道间串扰SSCRR,j测量不确定度模型[11]为

(12)

3 测量数据及处理

(1) 以FLUKE 9500A型示波器校准仪作为激励源,其技术指标为:

① 直流电压幅度范围:±(10 mV～1 000 V);

② 最大允许误差:±0.03%～±0.001%。

(2) 使用NI USB 6210型数据采集系统作为被测对象进行通道间串扰实验。其技术指标为[11]:

① 8个差分输入通道,ADC位数b=16 位,通道最高采样速率 250 kS/s;

② 输入量程范围:±0.2、±1、±5、±10 V;

③ 增益最大允许误差:±1.35×10-4、±9.5×10-5、±8.5×10-5、±7.5×10-5;

④ 偏移最大允许误差:±2.0×10-5、±2.0×10-5、±2.5×10-5、±4.0×10-5;

⑤ 随机噪声标准差:12 μV、26 μV、118 μV、229 μV;

⑥ 幅度最大允许误差(满度点):±88 μV、±310 μV、±1.41 mV、±2.69 mV;

⑦ 模拟带宽122.5 kHz,存储深度为n=4 096点数据FIFO。

(3) 选取NI USB 6210型数据采集系统的通道1为干扰激励通道,设定其量程范围为±10 V,激励信号为峰值幅度Es=10 V的直流信号。选取通道2为测量通道,设定其量程范围为±0.2 V,采集速率为125 kS/s,通道增益G=1,端接1 kΩ电阻,存储深度为n=3 000点数据。执行上述通道间串扰测量,获得串扰抑制比测量数据如表1所示。

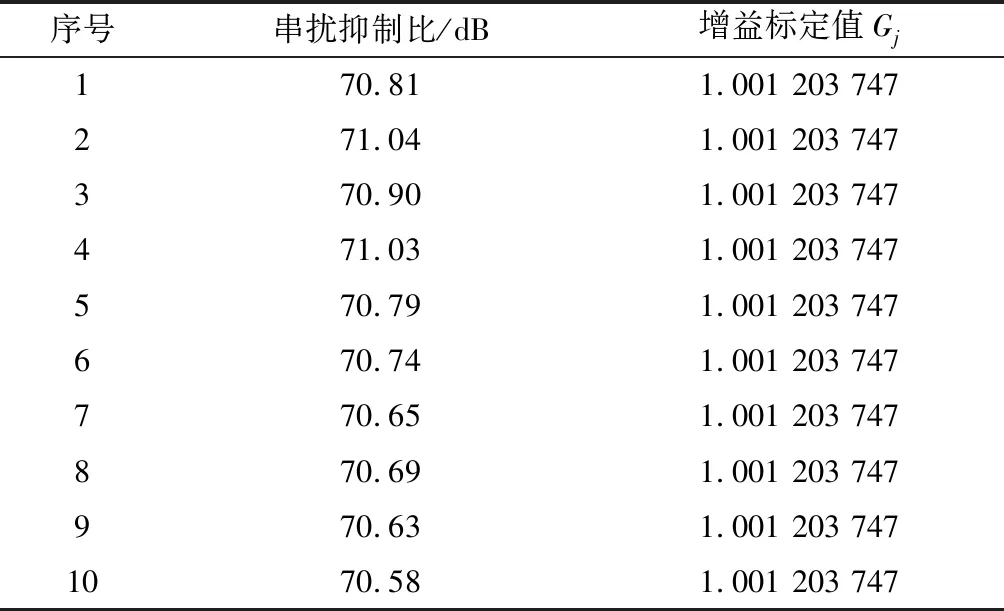
表1 通道间串扰测量结果

式(12)所示的不确定度模型增益Gj的不确定度u(Gj)可采用2种方式获得:① 使用说明书提供的通道增益计算通道间串扰,增益Gj属于给定量值,此时可使用说明书提供的该量值的不确定度;② 使用自身测量结果获得增益值计算通道间串扰,增益Gj不是给定量值,应评定其不确定度,具体参见文献[12]、文献[13]。

由通道增益Gj=1.001 203 747可以计算获得c1=8.675 446。由被测NI USB 6210型数据采集系统技术文件可知,其增益最大允许误差为±1.35×10-4,设其在[-1.35×10-4,1.35×10-4]内服从均匀分布,则有

(13)

u(Gj)=7.794×10-5,其自由度v(Gj)=∞。

激励信号幅度测量不确定度u(Es)可通过激励源指标获得,假设激励信号幅度Es在其最大允许误差限[-Δ1,Δ1]内服从均匀分布,可获得不确定度分量u(Es):

(14)

由激励源技术说明书可知[14],在Es=10 V时激励幅度最大允许误差为±Δ1=±2.69 mV,此时,有u(Es)=1.553 mV,c2=0.868 6,其自由度v(Es)=∞。通道1对Es的采样波形如图2所示,其对通道2造成的串扰采集波形如图3所示。

图2 串扰激励源采集波形

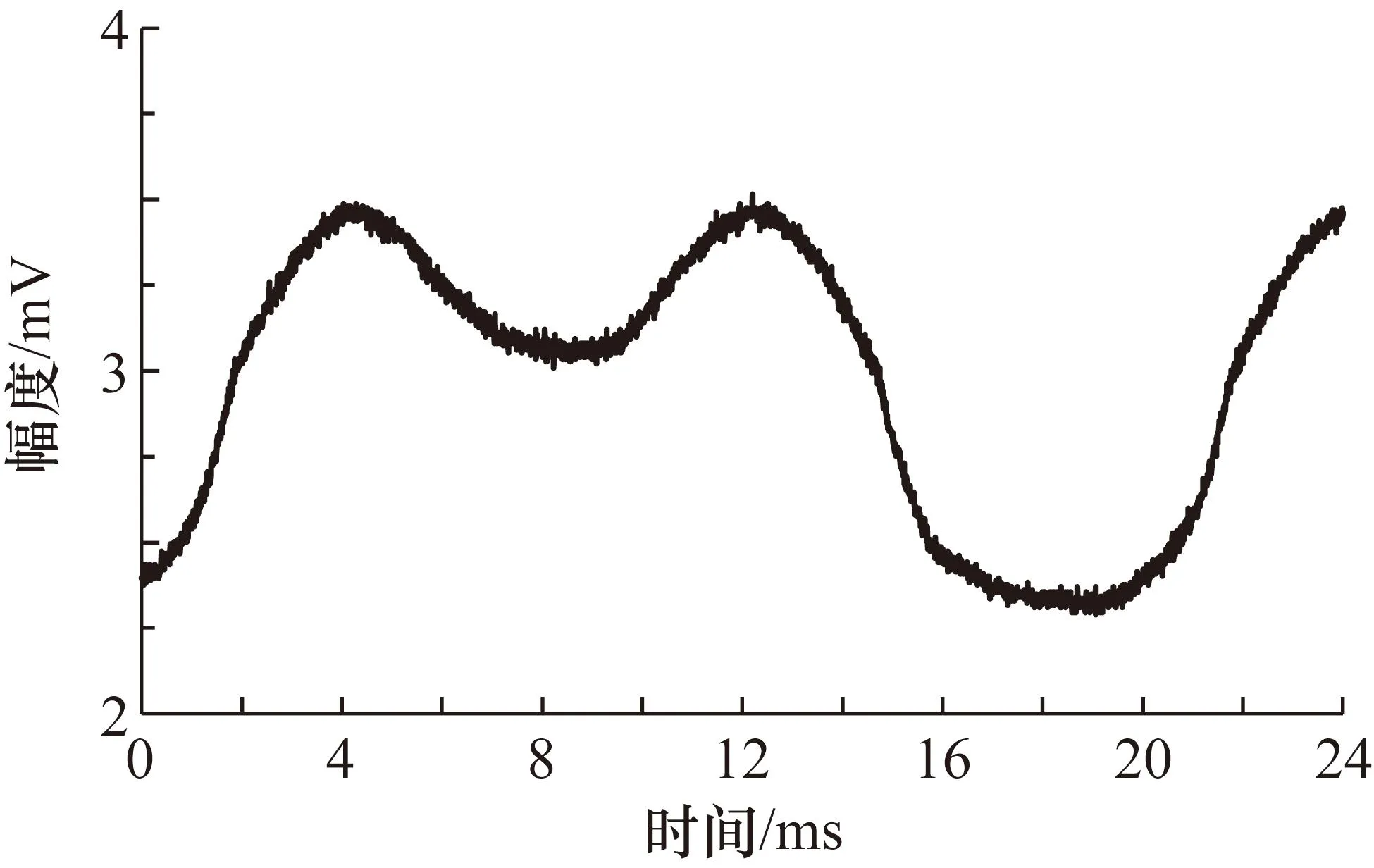
图3 串扰信号采集波形

由图2和图3可见,串扰激励信号的幅度波动变化可以非常小,但其串扰通道的测量序列则呈现不规则直流特征的波动现象,并非呈现平稳随机噪声特征。

激励信号的串扰测量幅值xjc的测量不确定度u(xjc)由xjc的实验标准偏差s(xjc)、数据采集系统测量分辨力误差±Δ2带来的不确定度ux2这两部分分量的最大者确定。

u(xjc)=max{s(xjc),uΔ2}

(15)

(16)

由所用A/D位数b=16位、量程范围±0.2 V可得:Δ2=0.4/216V=6.1 μV。可认为Δ2带来的不确定度uΔ2、在区间[-Δ2,Δ2]内服从均匀分布,则有

(17)

uΔ2=3.52 μV,其自由度v(Δ2)=∞。

则u(xjc)=0.398 5 mV,且

(18)

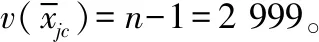
串扰源幅度E=0时,通道2的本底噪声干扰采集波形如图4所示。

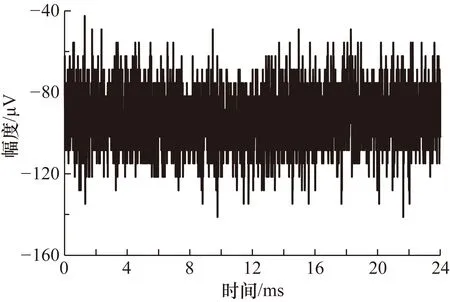
图4 本底噪声采集波形

由图4可见,信号量程小,数据采集系统的本底噪声采集序列的波动平稳,可近似看作非零均值的平稳随机过程。

(19)

由图4的测量序列可得:

数据采集系统测量通道本底噪声幅度xjz的不确定度u(xjz)可由实验标准偏差s(xjz)、数据采集系统测量分辨力±Δ2带来的不确定度uΔ2这两部分分量最大值确定。

u(xjz)=max{s(xjz),uΔ2}

(20)

可得u(xjz)=s(xjz)=14.122 μV。

(21)

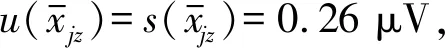
串扰抑制比SSCRR,j测量重复性带来的不确定度uA可由m次实验的实验标准差求出,即

(22)

(23)

4 合成不确定度计算

各不确定度分量评定完毕后,列出概算表,如表2所示。

表2 不确定度分量概算表

按式(12)计算通道间串扰抑制比合成标准不确定度uc=0.23 dB。由表2所述各个分量情况可知,干扰测量均值与测量重复性为主导分量,其他则为次要分量,可以忽略。由此可判定uc服从正态分布,按式(24)计算其有效自由度[10]为

(24)

5 扩展不确定度及测量结果的最终表述

选取置信概率p=95%,则由有效自由度veff(SSCRR,j)=38,从t分布表查得包含因子k=2.025,则可得,通道隔离度SSCRR,j的扩展不确定度为

U(SSCRR,j)=k×uc=0.46 dB

通道间串扰抑制比为

SSCRR,j=(70.81±0.46)dB (k=2.025,p=95%)

其中,±后面是扩展不确定度。

6 结束语

综上所述,在评价数据采集系统的通道间串扰时,影响评价结果的因素主要涉及到串扰激励幅度的不确定度、测量通道的增益及误差、测量分辨力及测量重复性等因素带来的不确定度。由图2和图3所示波形曲线可见,没有串扰的本底噪声,近似于平稳随机过程的白噪声,但并非零均值,属于有直流偏移的白噪声;其虽然是直流信号造成的串扰,有很大的主体部分体现的是直流特征,但也体现出波动波形的典型特征,计算获取该波形的有效值幅度,需要足够长的采样序列波形,这也是串扰测量中需要特别注意的。

本文所述测量过程中,测量重复性及串扰的影响占主导地位,两者的影响平分秋色,并占绝对优势,一方面说明抗干扰指标参数测量离散性较大,应该属于其不确定度中的主要分量;另一方面也说明测量序列测量重复性本身极为重要,而其他分量(如增益不确定度、干扰信号源幅度不确定度、本底噪声幅度等)对不确定度的影响可以忽略不计。

另外,对于干扰信号,不能简单按照随机噪声方式处理,同时,其不规则波动情况要求在获取干扰信号特征时,需要较长时间的数据采集测量,才能比较“完整”地获取和表征其特征参量。若采样序列比较短时,将只能获得其不规则波动的局部波形。因此,很难准确地估计其特征(如均值、标准偏差、波动范围等),这在实际工作中应予以注意。