基于解析法的激励器磁感应位置测量方法

陈丽武, 李劲林, 李怡杰, 钟舜聪

(1.福州大学 机械工程及自动化学院 福建省太赫兹功能器件与智能传感重点实验室,福建 福州 350108;2.福建省力值计量测试重点实验室(福建省计量科学研究院),福建 福州 350100;3.福建福光股份有限公司,福建 福州 350015)

磁悬浮技术[1]具有非接触、无需润滑、寿命长、无污染等优点,是促进我国制造业和航空航天事业发展的关键技术[2]。但由于电磁力存在各种非线性因素,其具有开环不稳定的特性。为实现闭环控制,需安装一定数量的运动量测量传感器并设计复杂的非线性控制器[3]。这不仅增加了磁悬浮平台的体积和成本,同时由于测量元件一般与驱动元件异位安装,给控制系统的设计增加了不小的难度。可能的解决方案是利用激励器自身电磁元器件对运动量进行测量。目前该领域的研究主要集中在磁悬浮轴承方面,且已取得了较大的成就[4-6],但针对磁悬浮平台的研究仍较少,如何利用平台自身元器件进行运动量测量是亟需解决的关键问题。

在磁悬浮轴承领域,位移自传感技术主要通过检测回路中电流变化来实时估计转子的位置。如马建国[7]、Schammass[8]等运用线性功放及高频小波注入法来测量位移,通过解调输出的高频小波信号即可完成位移估算。进一步,通过对上述注入小波的频率进行选择,可以在不影响控制的前提下实现位置估算[9]。随着电子技术的发展,开关功放因其高效率的特点被逐渐普及,由于开关功放本身就蕴含着高频开关纹波,因此也有研究人员致力于从开关纹波中提取转子位移信息。如Mizuno等[10]采用滞后型开关功放,在工作过程中保持电流纹波的幅度为定值,进而将悬浮装置的位置待测信息从上述功放的开关频率中解调出来。Yu[11]、Van Schoor[12]等运用脉宽调制(Pulse-Width Modulation,PWM)控制开关功放对开关纹波进行解调,并应用非线性参数估计法来估算转子的相对位置。为了对永磁偏置型磁轴承进行研究,Jiang等[13]利用双通道PWM解调方法获得其转子位移的自感知方法。为了实现更好的磁轴承性能,利用同步采样PWM开关频率,Hu等[14]对一种离散的电流估计方法进行了研究,以期减小自传感测量的路径。此外,结合力矩陀螺工作原理,赵建辉等[15]设计了一款差动电感式的位移传感器,实现集成一体化传感,并对其静态、动态和温度特性进行测试。然而,由于空间用磁悬浮平台激励器多采用洛伦兹力[16]结构,其与磁悬浮轴承的磁铁吸引结构具有较大区别,最为明显的区别是洛伦兹力激励器一般具有较大的磁场间隙,气隙不同位置的磁感应强度差别较大,磁悬浮轴承基于均匀磁场的各种自传感测量方法和理论难以直接应用于洛伦兹力激励器。

综上所述,本文基于磁感应原理对磁悬浮平台激励器的位置测量方法进行了研究,重点探索了激励器激励线圈与磁铁架以恒定速度相对运动时感应电压与相对位置的映射关系,并进行了仿真和实验验证。

1 激励器位置测量感应电压解析计算

1.1 洛伦兹力激励器

空间用磁悬浮平台一般通过多套洛伦兹力激励器的相互作用实现其浮台与基台间的六自由度运动控制。如图1所示,本文所述磁悬浮平台由三套二轴洛伦兹力激励器相互作用组成。各激励器分别由磁轭与永磁体构成磁铁架,形成闭合磁路在工作气隙处为激励线圈提供磁场。激励线圈与磁铁架无机械接触,当相互垂直的两个激励线圈分别通入电流时,即可在相互垂直的两个方向分别产生洛伦兹力以驱动激励线圈。

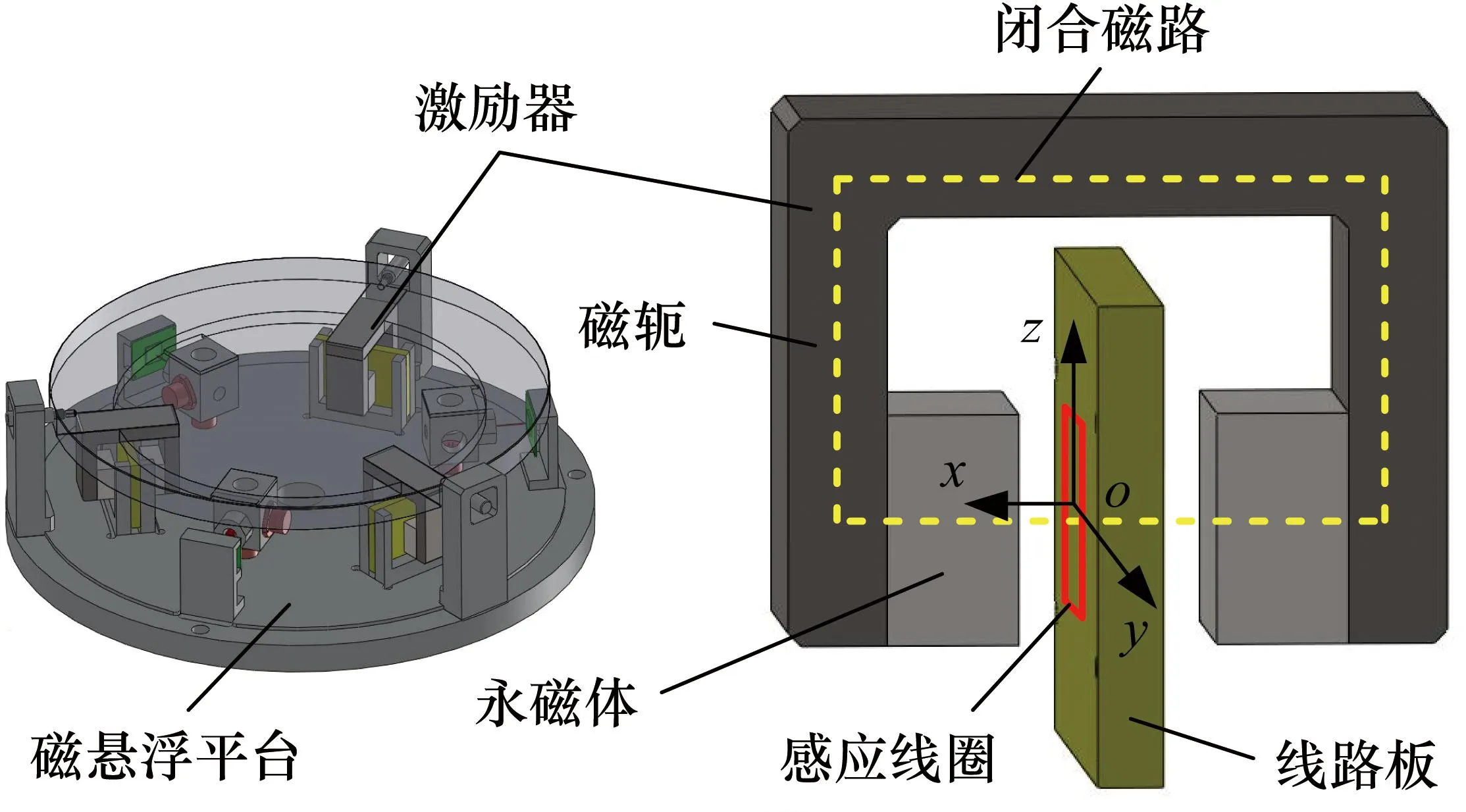
图1 磁悬浮平台及其激励器示意图

由于磁悬浮平台的浮子和定子在空间需具有约±10 mm的运动行程,且线路板具有约10 mm厚度,磁铁架闭合磁路存在较大的工作气隙。此外,激励线圈工作区域较大,气隙磁场漏磁增加,闭合磁路在工作气隙的磁场是不均匀的,即非线性的。而磁悬浮轴承由于工作气隙小,建模时认为工作气隙中磁场处处均匀。上述工作气隙磁场条件导致了本文所述激励器与磁悬浮轴承的自传感测量方法存在明显区别。事实上,本文所述激励器运动量测量方法正是基于工作气隙磁场的非均匀分布,探索激励线圈在运动过程中由于磁场非线性变化所引起的感应电压与其在磁场相对位置的映射关系。研究过程中如图1所示构建坐标系o-xyz,该坐标系的原点位于两个永磁体中间。如图中红色矩形框所示,感应线圈位于yoz所在平面,本文主要研究线圈沿y轴处于不同相对位置时所产生的感应电压。

1.2 激励器气隙磁场解析建模

为了对激励线圈电磁感应电压进行建模,首先需对感应线圈工作区域的磁场即气隙磁场进行建模。本文结合分子环流假说,利用Biot-Savart定律对电流元在气隙空间各点的磁感应强度进行计算。如图2所示,假设空间中存在一个电流为I的载流回路,其中任一电流元为Idl(l为载流环路),且该电流元在空间o1-x1y1z1坐标系中矢径为rI=[xI1,yI1,zI1],任取空间一点p,设其矢径为rp=[xp1,yp1,zp1],则由Biot-Savart定律可得其在点p处的磁感应强度B大小为

图2 载流回路及空间任意点示意图

(1)

式中:μ0为气隙磁导率。

对图2所示载流回路进行积分,即可得到载流回路在空间任意点产生的磁场强度如下:

(2)

在洛伦兹力激励器大间隙气隙磁场解析计算过程中,由于设计过程中充分考虑了磁轭的磁饱和问题,因此可认为磁轭不会出现磁饱和现象,将磁轭磁导率视为无穷大。进一步,利用镜像法对由永磁体和磁轭构成的磁铁架进行简化,考虑永磁体沿x轴方向进行充磁,简化模型以永磁体和磁轭的接触面为镜面,将磁轭等效为与永磁体体积大小相等的两块永磁体。如图3所示,永磁体的横截面边长分别为2a和2b,厚度为h,等效永磁体的大小与其一致,边长与厚度同样分别为2a、2b和h。下面利用分子环流假说和Biot-Savart定律对上述等效模型进行三维磁场解析建模,以获得工作气隙各点的磁感应强度[17-18]。

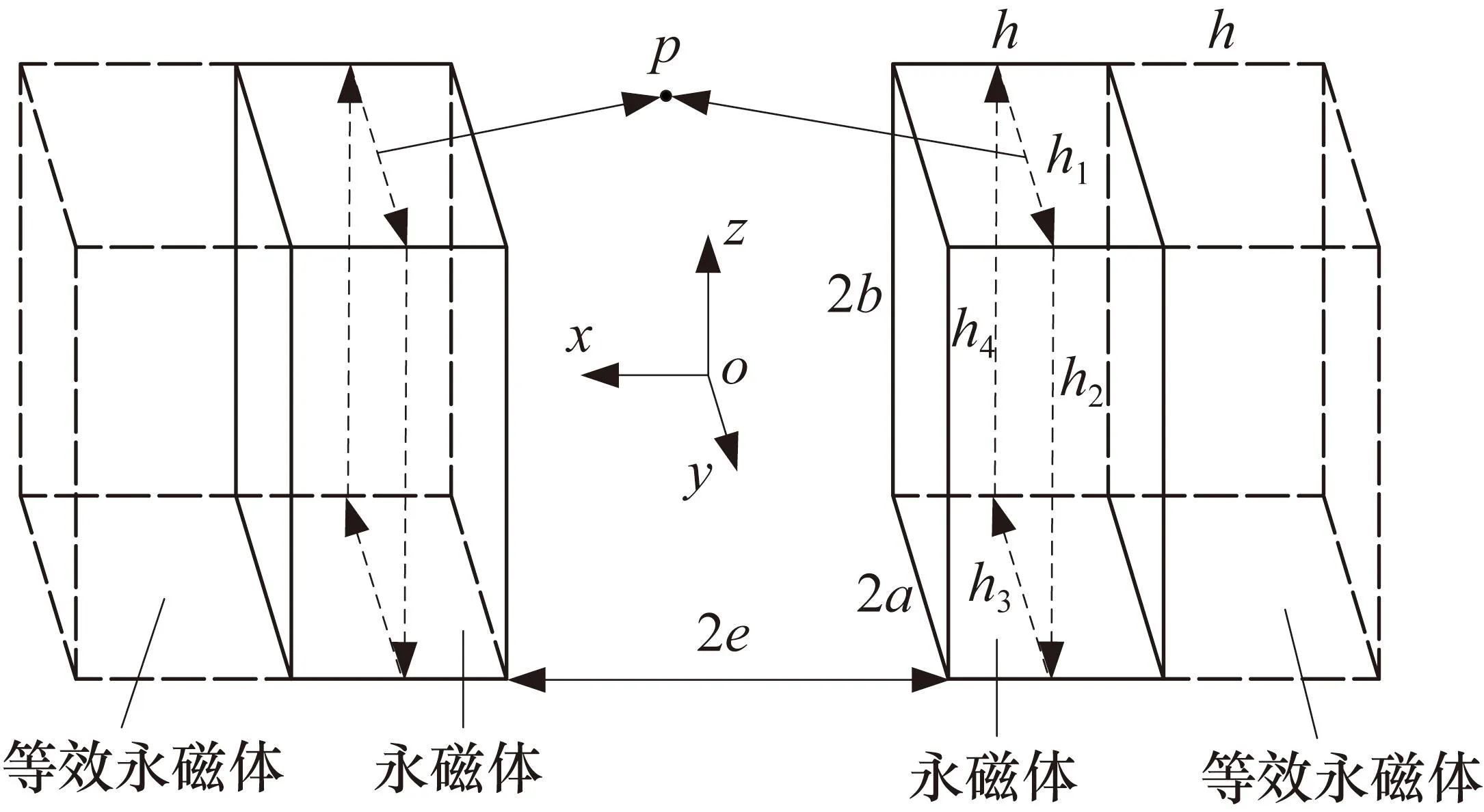
图3 磁铁架等效简化模型示意图

依据分子环流假说,将如图3所示永磁体横截面对空间点的磁场作用等效为横截面外围边缘对空间点的作用,将横截面上的电流分为闭合的h1～h4这4段分别进行分析。假设表面环流的电流薄层厚度为dx,则其环流大小可表示为

I=Jsdx

(3)

式中:Js为等效电流密度;I为等效环流大小。

首先考虑左侧的永磁体及其等效永磁体在工作间隙中任意点p(x0,y0,z0)的磁场强度Bl,可表示为

(4)

式中:Blx、Bly和Blz分别为在p点沿x、y、z方向的磁场强度值;i、j和k分别为沿上述3个坐标轴方向的单位向量;e为左侧永磁体到气隙中间点的距离;h为永磁体厚度。

进一步,先考虑p点受h1段作用,对应Bl在3个坐标轴方向的值分别为

(5)

同理,可分别计算h2、h3、h4段在p点沿各个坐标轴方向的磁感应强度分量。由于本文仅考虑感应线圈沿y轴运动的情况,位置测量过程中仅对x方向的磁场进行切割,故整理给出磁感应强度沿x轴方向的解析方程:

Blx=K[ψ(x0,y0-a,z0-b)-ψ(x0,y0+a,z0-b)+
ψ(x0,z0-b,y0-a)-ψ(x0,z0+b,y0-a)-
ψ(x0,y0-a,z0+b)+ψ(x0,y0+a,z0+b)-
ψ(x0,z0-b,y0+a)+ψ(x0,z0+b,y0+a)]

(6)

式中:

同理,可计算整理得到右边永磁体在点p(x0,y0,z0)处产生沿x轴方向的磁感应强度为

Brx=K[ψ(x0,y0-a,z0-b)-ψ(x0,y0+a,z0-b)+
ψ(x0,z0-b,y0-a)-ψ(x0,z0+b,y0-a)-
ψ(x0,y0-a,z0+b)+ψ(x0,y0+a,z0+b)-
ψ(x0,z0-b,y0+a)+ψ(x0,z0+b,y0+a)]

(7)

式中:

由于左右两块永磁体为串联布置,在工作气隙内所产生的磁场方向相同,可通过叠加原理计算yoz平面任一点沿x轴方向的Bx大小:

Bx=Brx+Blx

(8)

利用式(8)所示工作气隙磁场计算方法,对某磁铁架气隙磁场进行计算,以o-xyz坐标原点为中心,在y和z轴±100 mm范围内每隔0.1 mm计算一个点,得到上述yoz平面的磁感应强度分布如图4所示。由图4可知,在yoz平面的磁场分布具有较为强烈的变化,中心位置的磁场强度在0.34 T左右,外围的磁场强度基本为零,且上述变化并非均匀的。当感应线圈沿y轴由y1位置以特定速度向y3位置运动时,必然会有明显变化的感应电压产生。本文即利用上述变化的感应电压对线圈的相对位置进行评估。

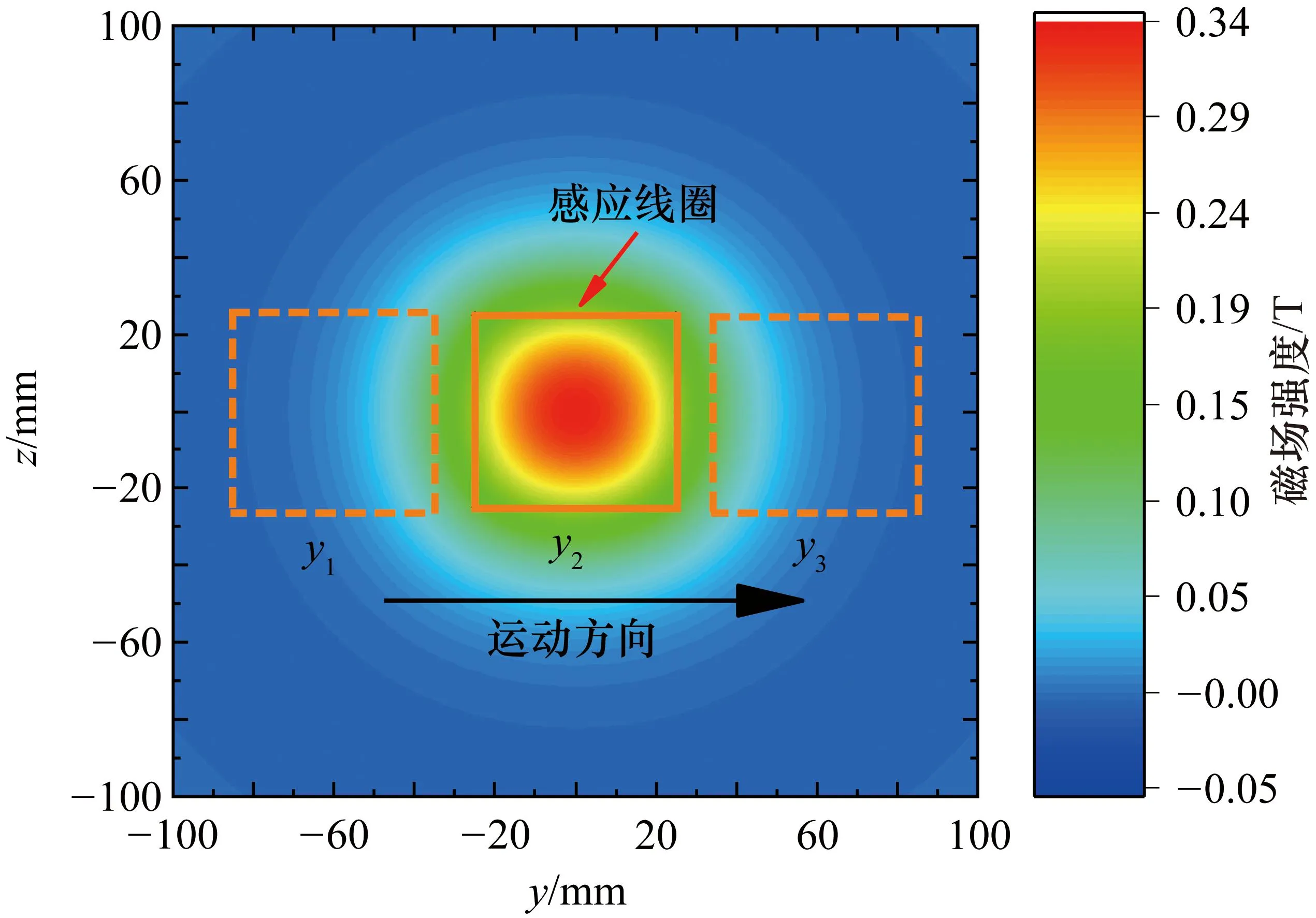
图4 yoz平面的磁场分布及感应线圈运动示意图

1.3 感应电压计算及位置测量分析

根据电磁感应定律,感应电压与回路中磁通随时间的变化率成正比:

(9)

式中:u为感应电压;N为线圈匝数;Φ为磁通;t为时间。磁通Φ计算公式如下:

(10)

式中:S为线圈实际作用面积。

为获得运动线圈的感应电压,首先需要获得作用在线圈上的磁场的变化。对式(9)进行推导,将式(9)中对时间t的全导数展开为对时间t的偏导数:

(11)

由于激励线圈在测量过程中大小不变,上式中的第二项偏导为0。

感应线圈为多层平面线圈,同一平面各匝线圈面积不同,所包围的磁通也不同。为简化计算,将平面线圈每匝的有效面积等效为Sr,其值取为平面线圈最外圈面积大小的93%。计算过程中,本文首先分别对面积Sr范围内n个小区域(0.01 mm2)的磁通量进行计算,且用各小区域中心点的磁感应强度替代该小区域的磁感应强度,将上述各小区域的磁通相加得到整体磁通,表示为

(12)

进一步,线圈沿y轴匀速直线运动,则上式中第i个小区域的磁感应强度变化可表示如下:

ΔBi=Bi(k+1)-Bi(k)

(13)

式中:Bi(k)为第k时刻第i个小区域的磁感应强度;Bi(k+1)为第k+1时刻该小区域的磁感应强度。由于线圈沿y轴匀速运动,上述磁感应强度变化实际上是该小区域沿y轴运动vt所产生的磁感应变化。结合式(9),可将线圈在第k时刻所产生的感应电压表示为

(14)

式中:Bi(k+1)、Bi(k)可分别根据第i个小区域在该时刻的位置通过式(8)计算得到。

利用上述计算公式,对某线圈在工作气隙中沿y轴以恒定速度直线运动时,在y轴±100 mm范围内一共计算了2 001个时间点的感应电压值,如图5所示。

图5 感应线圈沿y轴运动时感应电压大小变化曲线

观察图5可知,感应电压以原点为中心,呈中心对称分布。其中,AB段和EF段这两个区域对应磁场外围区域,感应电压值本身很小且变化很小,该区域为小变化区,不利于开展位置测量;在BC段和DE段这两个区域,感应电压变化剧烈,具有明显的非线性特性,且在C点和D点这两个位置分别得到最小值和最大值,不利于开展位置测量;而在中间CD段这个区域范围内,随着位置变化,感应电压从最小值变化到最大值,具有较好的线性度,该线性区是较为理想的感应测量区。磁悬浮平台的运动行程为±10 mm,由图5可知所提出的感应测量方法可实现其位置测量。

2 激励器位置测量仿真与实验设置

2.1 实验样机

为了对上述磁感应测量中感应电压的计算方法进行验证,本文设计实验样机进行了有限元仿真和实际测量实验。实验样机的关键参数如下:永磁体的牌号为N35,矫顽力设置为760 kA/m,剩磁为0.801 T,两块尺寸均为40 mm×40 mm×20 mm,磁轭的厚度为20 mm,工作间隙为30 mm;激励线圈为4层PCB板,每层含15匝感应线圈,线圈的边长等效为95 mm。

2.2 有限元仿真设置

本文利用Ansoft 软件对激励器的气隙磁场及线圈感应电压进行有限元仿真[19],对数值进行分析时主要利用Maxwell方程组来对网格进行求解和计算:

(15)

式中:▽×为旋度算子;▽·为散度算子;H为磁场强度;J为电流密度;D为电位移矢量;E为电场强度;ρ为体电荷密度[20]。

仿真过程中,首先利用Solidworks对激励器进行建模,进而将所建立的模型利用“modelor——import”导入到Ansoft软件的操作界面中。进行的仿真分析步骤主要包括预处理、求解运算和后处理3个部分,具体如下。

(1) 预处理。

在创建分析文件后,选择Transient作为求解器,导入文件后设置两块永磁体的材料为NdFe35,磁轭材料为steel_1008,线圈材料为Cu。进一步,进行网格划分,如图6所示,对线圈、永磁体和磁轭的网格划分进行精细化处理,对应最大单元长度分别设置为1 mm、2 mm和5 mm,运动域和边界的最大单元长度分别设置为20 mm和50 mm。

图6 激励器电磁感应有限元仿真示意图

(2) 求解运算。

在上述预处理后,对感应线圈添加绕组及电流等,其中绕组设置为60 匝,并如图6所示创建求解域及运动物体的band域。由于线圈沿y轴匀速直线运动,设置线圈速度为1.13 cm/s。此外,设置大小为0.5 ms/step的分析步,保存后即开始计算。

(3) 后处理。

待上述计算过程完成后,在Field中查看磁场强度和磁场密度云图,在Results中查看感应电压计算结果。

2.3 物理实验设置

结合加工的实验样机,设置物理实验测量装置如图7所示。其中,永磁体和电工纯铁(DT4)构成的C型磁铁架被安装在基础上;含有感应线圈的多层线路板则被安装在位移平台上,用于实现在气隙磁场中的匀速运动。位移平台由其驱动模块驱动,通过电机(Oriental,57HS56-3004-001) 的转速控制实现线路板匀速前进。进一步,在测量过程中实时通过位移测量模块和电压采集模块同步采集线路板所在的位置和感应电压值。如图7中所示,位移测量模块通过JU-MAOAM-D100激光位移传感器实现,感应电压的采集则通过信号处理电路和STM32开发板实现,采集到的位置信号和感应电压信号均发送到上位机进行存储和处理。

图7 磁感应位置测量实验装置示意图

3 实验结果分析

如上文所述,设置了有限元仿真和物理实验对本文所提出的位置测量解析计算方法进行验证。实验过程中,设置激励线圈相对磁铁架以1.13 cm/s的速度匀速前进,线圈的感应电压值经过信号处理电路被放大约290倍。进一步,激励线圈沿y轴匀速运动±100 mm,通过解析计算、有限元仿真和物理实验的测量结果如图8所示。由图8可见,不同位置由解析计算得到的感应电压理论值与仿真和实验测量结果基本一致,特别是图5所示的CD线性段,解析计算结果与实验测量结果十分接近。

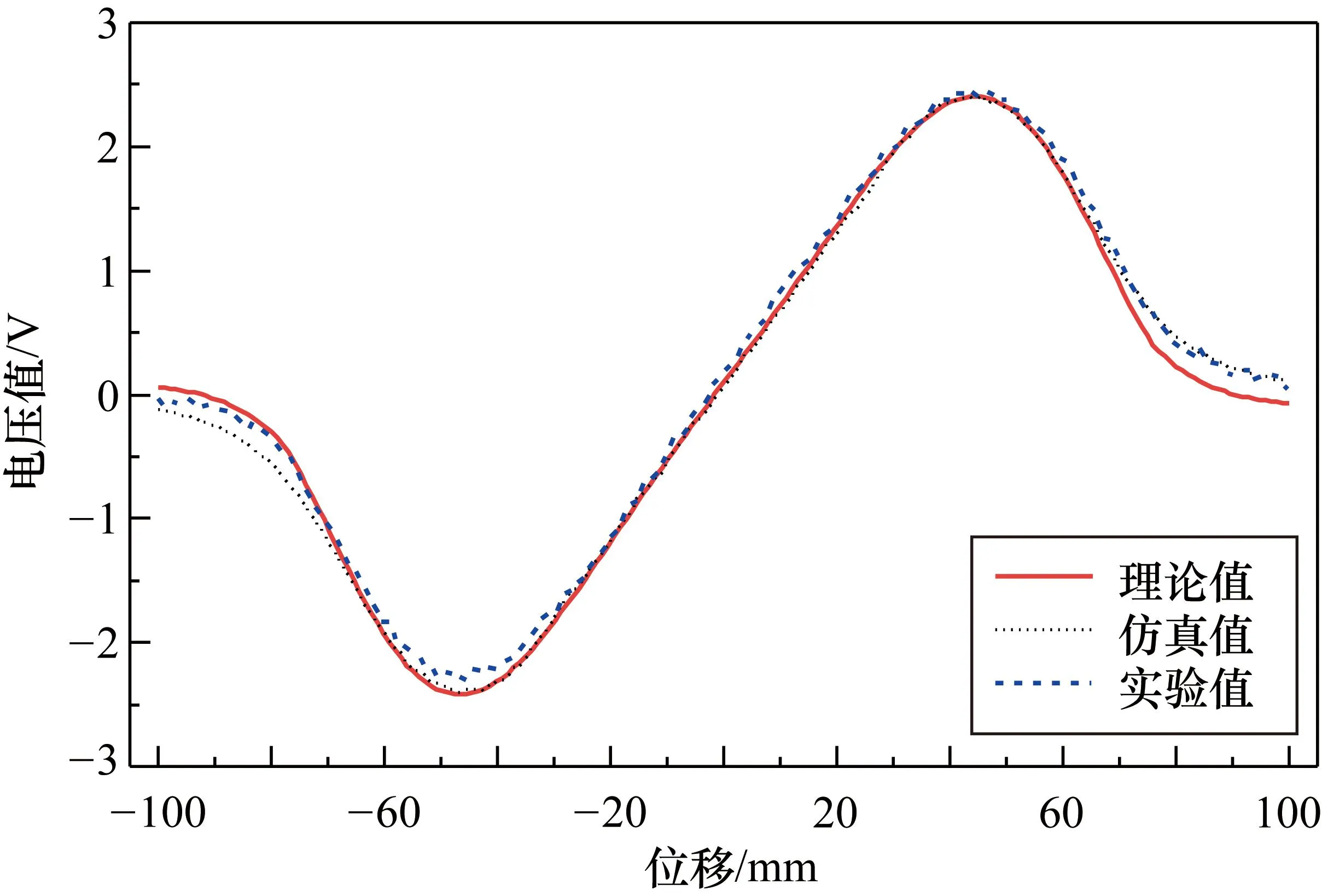
图8 不同方法得到的感应电压曲线

进一步,通过满量程误差δap、δfp、δaf(如图9所示)分别展示了解析计算结果、仿真计算结果与实验测量结果间的相对误差,其计算公式分别为

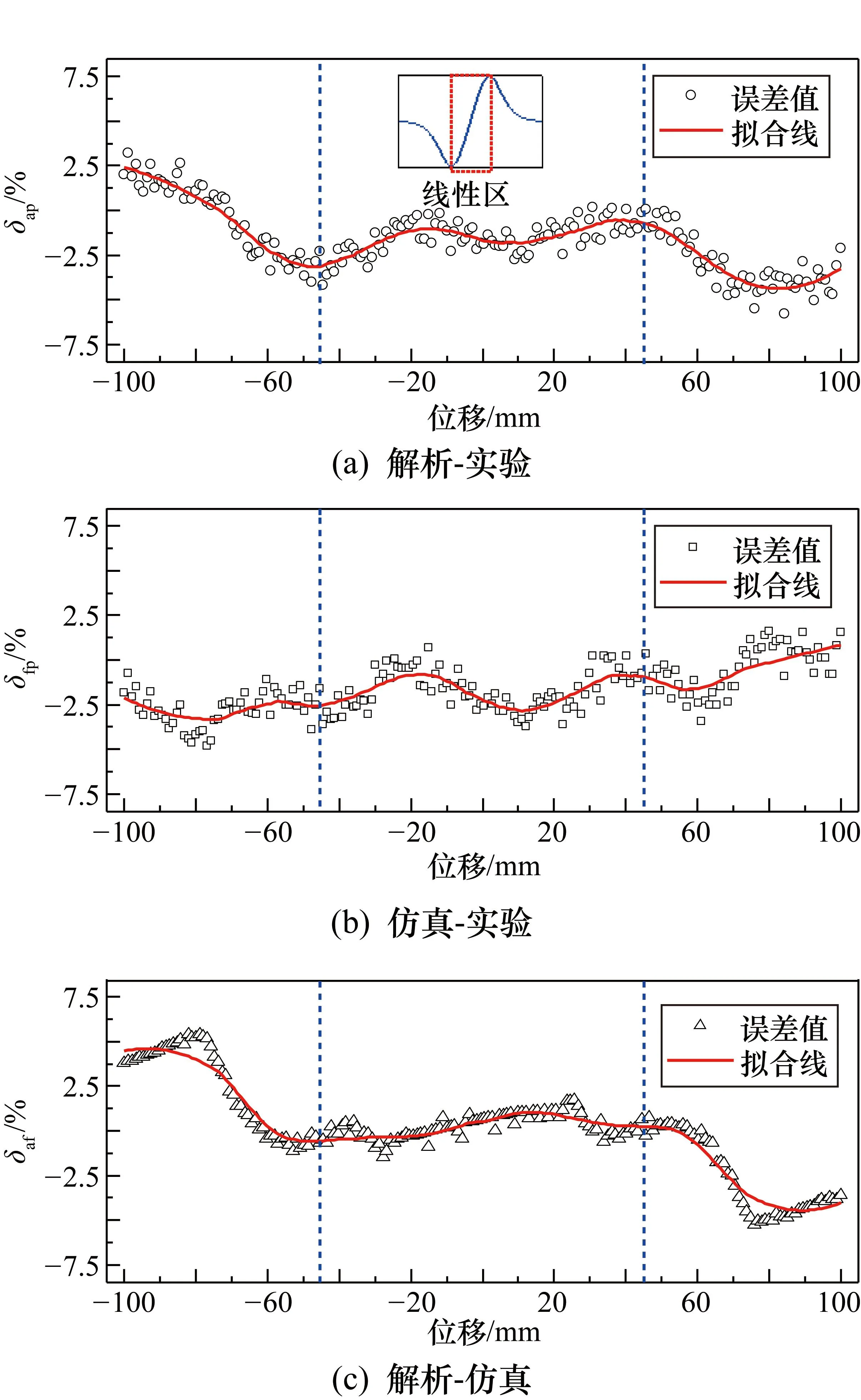
图9 解析、仿真及实验测量结果间的误差曲线

(16)

式中:Va、Vf、Vp分别为解析、仿真和实验测试得到的感应电压值;Vfmax、Vfmin、Vpmax、Vpmin分别为仿真和样机实测得到的电压最大值和最小值。由图9(a)可知,解析计算结果与实验测量结果的满量程误差δap基本保持在±5%以内,特别地,较为理想的CD段感应测量线性区内误差<5%。此外,由图9(b)和图9(c)可知,仿真计算结果与实验测量结果及解析计算结果的误差亦具有相同的分布。进一步,结合空间磁场对称性,可见不同位置的误差呈现对称分布,且与图5所示分区基本一致,误差较小的区域主要分布在中间的线性区。综上可知,本文所提出的激励器位置测量感应电压解析计算方法是正确可行的。

进一步,为了对感应线圈所产生的反向磁场大小进行评估,将其简化等效为一个边长为95 mm的平面矩形线圈,并依据Biot-Savart定律得到其在中心处的总体磁感应强度,计算公式为

(17)

式中:N为线圈匝数;μ0为真空磁导率;I为线圈电流;la为线圈边长。依据前文实验可知,感应线圈所产生的感应电压最大值约为8.2 mV,线圈电阻约为8.63 Ω。根据式(17)计算可得感应线圈所产生的磁场大小约为0.84×10-3mT,远小于气隙磁场中心处300 mT磁感应强度,因此在本例中线圈由于感应电流产生的磁场可忽略不计。当然,上述由于感应电流产生的磁场在设计过程中是不可忽视的,当感应线圈的匝数、电流、速度以及尺寸达到一定数量时,所产生的磁场强度就会对激励磁场产生影响。

在上述研究过程中,本文提出了一种激励器磁感应位置测量解析计算方法。当建立上述磁感应电压值与激励线圈相对位置映射关系以后,便可以利用感应电压值的测量来精确获取线圈的相对位置。但针对实际测量应用,上述研究显然还有很多不足,最为关键的是本例在计算过程中要求线圈的运动速度和方向是恒定且已知的,并未实现真正意义的自我测量。可行的解决方案是引入新的测量电信号,如探索多感应线圈相互配合测量,进而消除运动速度等对位置测量的影响。

4 结束语

本文基于分子环流法、镜像法以及Biot-Savart定律建立了磁悬浮平台激励器气隙磁场精确解析模型,并结合法拉第电磁感应定律,得到激励线圈在单自由度方向以恒定速度运动时的感应电压计算方法,获得激励线圈感应电压与相对位置的映射关系。最后,利用有限元仿真和物理实验对解析模型进行了验证。结合上述研究内容,本文得出的结论具体如下。

① 解析计算结果与实验测量结果相对比,满量程误差在±5%以内,解析解与实际测量结果基本吻合,特别地,拟用于位置测量的理想线性区的误差在5%以内。此外,解析计算结果与仿真解算结果的误差分布范围与此基本一致。由此,通过提取感应线圈两端的电压可以对线圈在工作气隙的相对位置进行测量,即所提出的激励器磁感应位置测量方法是可行的。

② 上述位置测量方法虽然是可行的,但距离实际应用仍有很大的差距,主要的不足在于当前的解析计算方法仍然依赖于线圈的速度值,在速度未知的情况下仍不能对位置进行测量。此外,本研究案例的磁场建模仅考虑了yoz平面所受的x方向磁场,如要实现磁悬浮平台的六自由度测量,须完善整个空间的磁场模型,进而建立线圈六自由度位姿与感应电压的映射关系。