Gamma-Gamma 湍流下新型脉冲位置调制性能分析

肖冬亚，钟月曦，安喆

（1 长春工程学院 电气与信息工程学院，长春 130012）

（2 长春工程学院 机电工程学院，长春 130012）

0 引言

自由空间光（Free Space Optical，FSO）通信具有频带宽、容量大、速率高、抗电磁干扰、功耗低、终端小、安装方便、保密性好等优点［1-3］，应用前景广阔，因此受到国内外研究人员的广泛关注。但激光束在大气信道传输时，会因大气衰减、大气湍流等因素导致通信性能降低，为此，研究者们采取了一系列措施，其中最为重要的关键技术之一就是调制技术［4］。

强度调制/直接探测（Intensity Modulation/Direct Detection，IM/DD）系统结构简单、容易实现，在FSO通信领域应用最为广泛，其典型调制方式有开关键控（On-Off Keying，OOK）调制、单脉冲位置调制（L-level Pulse Position Modulation，LPPM）、差分脉冲位置调制（Differential Pulse Position Modulation，DPPM）、多脉冲位置调制（Multiple Pulse Position Modulation，MPPM）、数字脉冲间隔调制（Digital Pulse Interval Modulation，DPIM）方式等。应用于IM/DD 光通信系统最早、最简单的是OOK，但是其功率利用率太低、抗干扰能力较差。LPPM 具有优越的功率利用率，但以付出大量带宽为代价［5］，传输容量上也难以达到FSO通信的要求［6］，并且解调时需要严格的符号同步，增加了系统的复杂度。DPPM 是对LPPM 的改进，相对提高了带宽利用率［7］，不需要符号同步，但在编码过程中仍会产生多余的“0”时隙，使得这种调制方式在传输容量、带宽利用率上不够高。MPPM 进一步提高了带宽利用率［8］，但其差错性能欠佳，而且需要严格的符号同步，增加了系统的复杂度。

针对传统脉冲位置调制（Pulse Position Modulation，PPM）方式存在的不足，国内外学者提出了一些改进的PPM 方式。FAN Yangyu 等［9］提出了脉冲位置宽度调制（Pulse Position Width Modulation，PPWM），可以降低LPPM 带宽需求，但仍需要严格的符号同步，增加系统的复杂度；LIAO Renbo 等［10］提出了反向差分脉冲位置宽度调制（Reverse Differential Pulse Position Width Modulation，RDPPWM），解决了符号同步问题，但其带宽利用率、功率利用率和差错性能均劣于OOK；WANG Yan 等［5］提出了n脉冲XPPM 调制，可以提高MPPM 的带宽利用率，但也需严格的符号同步；IDRIS S 等［11］提出了混合多脉冲幅度和位置调制（Hybrid Multiple Pulse Amplitude and Position Modulation，H-MPAPM），可以提高传输容量和带宽利用率，但需要在接收端定期估计多个阈值水平以及需要实现复杂的同步方案，解调较困难。此外，SHARMA K 等［12-13］、JIANG Ting 等［14］、MAGIDI S 等［15］对基于PPM 的射频-自由空间光（Radio Frequency-Free Space Optical，RF-FSO）通信的混合调制进行了研究，在一定信噪比下其性能有所提升，但复杂性也相当高。本文从改进PPM 的性能出发，结合DPPM 不需要符号同步和MPPM 带宽利用率高的优势，提出一种新型差分脉冲位置调制（Novel Differential Pulse Position Modulation，NDPPM），在不增加系统复杂度的前提下，可较大程度提升系统的传输容量和带宽利用率；并从丰富理论和实际应用的角度，研究了其具体映射关系及符号结构，分析了其调制性能，并与其他几种调制方式进行了比较；推导了Gamma-Gamma 湍流信道下FSO 通信系统的平均误时隙率和误包率模型。根据上述推导的模型，进行了差错性能仿真，分析了湍流强度、传输距离和调制阶数对NDPPM 系统差错性能的影响，并对比分析了NDPPM 和其他几种调制方式的差错性能。

1 符号结构

LPPM 是指将n位二进制数组映射为由2n个时隙组成的时段上某一个时隙处的单个脉冲信号，其他时隙上均没有脉冲信号。DPPM 是在LPPM 基础上改进的一种调制方式，通过删除对应的LPPM 信号中1 时隙后面的所有0 时隙而得到。MPPM 方式是将n位二进制数组映射为由M个时隙组成的时段上同时出现k个脉冲的组合，，记为(M，k)MPPM，最常见的形式是k=2 的二脉冲。为了提高调制性能，本文提出一种新型调制方式，即NDPPM 方式。在该方案中，将n位二进制数组X=(x1，x2，…，xn)分别映射到一个信息帧上，具体的映射关系如下：当L<2n-1时，n位二进制数据映射的数据帧起始位为0，末位为1，中间位是0，0 的个数为L个；当L≥2n-1时，n位二进制数据映射的数据帧起始位为1，末位为1，中间位是0，0 的个数为L-2n-1；其中，L=xn+2xn-1+…+2n-1x1，然后按照上述调制好的信号序列发送数据。

NDPPM 信号可以表示为

式中，M为一帧时隙数，P为平均功率；[c0，c1，…，cM-1]为NDPPM 码字，rect(t)为持续时间为τ的单位幅度矩形脉冲，即

表1 是当n=3 时，OOK、LPPM、DPPM、NDPPM 和（5，2）MPPM 几种调制方式的编码映射关系，相应的符号结构如图1。

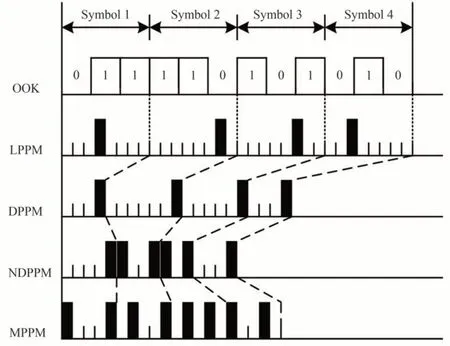
图1 各调制方式的符号结构Fig.1 Symbol structure of different modulation schemes

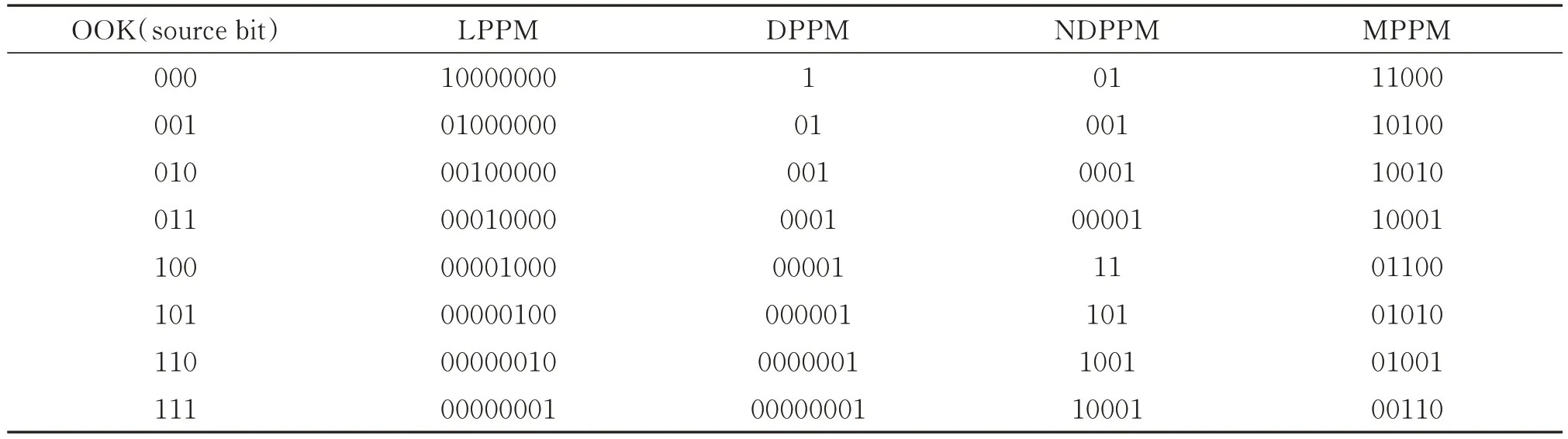
表1 各调制方式的映射关系Table 1 Mapping relation of different modulation schemes

2 调制性能分析

2.1 传输容量

在时隙宽度相同的条件下，一般用比特率来衡量各调制方式的传输容量。设时隙宽度为τ，调制阶数为n，一帧信息时隙数为M=2n。故采用OOK 时，其传输容量为

同理，可得四种PPM 方式的传输容量分别为

由于DPPM 和NDPPM 的符号长度不固定，故用平均符号长度计算。各调制方式对OOK 归一化的传输容量如图2。通过图中曲线可以看出，随着n的增大，四种PPM 方式的传输容量都呈下降趋势；其中LPPM 方式的传输容量最低，其次是MPPM 和DPPM，NDPPM 的传输容量最高，在n=6 时，大约是LPPM传输容量的4 倍，是MPPM 和DPPM 传输容量的2 倍以上。因此，在相同时间内，可以传输更多的NDPPM符号，NDPPM 同DPPM 一样每帧均以“1”时隙结束，同样不需要符号同步，在提高通信性能的同时并不增加系统的复杂度。

图2 各调制方式的传输容量比较Fig.2 Comparison of transmission capacity of different modulation schemes

2.2 带宽需求

激光通信系统传输信息需要一定的带宽，而且这个带宽越小越好。假设每一符号发送n比特信息，传输比特率为Rbbit/s，如果以功率谱的第一个零点来算，OOK 的带宽BOOK≈Rb。由于光信号脉冲时隙宽度较窄，各调制方式所需带宽可以定义为其时隙宽度τ的倒数，则OOK 所需的带宽为BOOK≈1/τOOK=Rb，τOOK为OOK 调制的时隙宽度。在信源比特率相同的条件下，比较这几种调制方式的带宽需求，可得LPPM 调制的带宽需求为

同理，可得DPPM 和NDPPM 的带宽需求分别为

对于MPPM，M、k和n三者满足关系，M为满足此关系中，取值最小的M。因此，当n取不同，对应的M不同，根据定义可得MPPM 的带宽需求为

各调制方式对OOK 归一化的带宽需求如图3。通过曲线可以看出，随着n的增大，各调制方式的带宽需求均增大；LPPM 的带宽需求最高，其次是DPPM、NDPPM 和MPPM。NDPPM 的带宽需求在n<6 时和MPPM 相当；n≥6 时，略高于MPPM，但明显低于LPPM 和DPPM，仅为LPPM 的1/4，为DPPM 的一半。

图3 各调制方式的带宽需求比较Fig.3 Comparison of bandwidth requirement of different modulation schemes

2.3 平均功率需求

在信息速率相同的条件下，从统计意义上比较不同调制方式的平均发射功率需求。设峰值功率为Pt，二进制信息比特“0”和“1”等概率出现，且发送“1”时需要峰值功率Pt，发送“0”时不需要功率，则OOK 的平均功率为POOK=Pt/2。同理，可得四种PPM 方式的平均功率分别为

MPPM 调制方式中，当n取不同值，对应的M不同，计算方法如前所述。对OOK 归一化的平均功率需求如图4。从图中可以看出，随着n的增大，四种PPM 方式的平均功率需求都呈下降趋势；LPPM 的平均功率需求最低，其次是DPPM、NDPPM 和MPPM。当n>3 时，NDPPM 的平均功率需求明显低于MPPM；当n=7 时，其平均功率需求近似为MPPM 的1/3；当n=9 时，其平均功率需求仅为MPPM 的1/6。

图4 各调制方式的平均功率需求比较Fig.4 Comparison of average power requirement of different modulation schemes

3 差错性能分析

3.1 系统和信道模型

采用IM/DD 方式的FSO 通信系统模型如图5。输入的二进制数据经过调制模块进行编码、调制，然后加载到激光束上，通过光学发射天线发射出去，经过大气信道传输，然后由接收天线接收信号，经过光电探测器将光信号转换为电信号，再经过解调模块进行抽样判决、解调、译码，从而恢复出原始信号。

图5 FSO 光通信系统模型Fig.5 FSO communication system model

激光信号在大气信道传输时，不可避免地会受到大气湍流的影响。大气湍流是一种随机的空气运动状况，湍流的随机变化会引起折射率随空间和时间而随机变化，从而导致激光束的无规则起伏。为便于分析，假定信道无记忆平稳遍历，信道状态信息在发射端和接收端都可用，噪声为加性白高斯噪声（Additive White Gaussian Noise，AWGN），忽略信道时延及指向偏差，则接收到的电信号可以表示为［16］

式中，s=ηI表示接收端光强增益，η为光电转换效率，I为接收光强，x∈(0，1)为调制信号，n为方差为的高斯白噪声。

接收端光电探测器将接收到的光信号转换为电信号，由光电探测理论可知，平均接收光功率与光强的关系为Pr=Ar⋅I，其中Ar为探测器的面积［17］。光电探测器经光电转换后接收的光电流为is=ηPr=ηArI，可得电信号的平均功率为，则电信噪比可以定义为

令Ar=1，q=1，可得归一化的平均电信噪比（Signal-to-Noise Ratio，SNR）为

光波在大气中传输时，受到大气湍流的影响，导致光强度发生起伏，弱湍流信道下，人们普遍认为光强服从对数正态分布［18］；强湍流下，光强不再服从对数正态分布，而是更接近K 分布［19］。多项研究表明，Gamma-Gamma 模型使用范围较广，并且和实际测试数据较一致，可以较为准确地描述从弱湍流至强湍流的光强起伏特性［20-22］，其概率密度函数可以表示为

式中，Γ( ⋅)为Gamma 函数，Kv( ⋅)为第二类修正贝塞尔函数，α和β分别表示大尺度湍流和小尺度湍流的有效数量。忽略内尺度影响下，α和β分别表示为［3，23］

3.2 差错性能推导

大气信道中噪声和湍流效应会导致接收光信号衰落、光强随机起伏，进而导致判决出错，引起误码。由于信道参数的随机变化，信噪比也会发生变化，分析系统的差错性能时，一般取统计平均，系统的平均误时隙率可表示为［24］

式中，Pse为给定调制方式的条件误时隙率，f(I)为Gamma-Gamma 湍流信道下光强I的概率密度函数。

为便于分析，假设1）不存在多径效应；2）接收机带宽足够宽；3）收发对准，不考虑抖动；4）背景光只考虑其噪声影响；5）噪声n(t)为AWGN，方差为，则抽样判决器的输入端在发送脉冲“1”时为，不发送脉冲时为n(t)，其中Pt为抽样判决器输入端信号峰值功率［25］。

若设判决门限为b，“0”被误判为“1”的概率记为P1/0，“1”被误判为“0”的概率记为P0/1，则有

若发送0 和1 的概率分别为P0和P1，且P0+P1=1，则总的误时隙率为

，可得OOK 的误时隙率为

同理，可得其他几种调制方式的误时隙率分别为

对式（26）～（30）两边关于判决门限b求导，并令其导数等于0，可得最佳判决门限为

式中，r表示“0”出现的概率和“1”出现概率的比值，不同调制方式的r值不同，分别为rOOK=1、rLPPM=2n-1、rDPPM=(2n-1 )/2、rNDPPM=2n-13、rMPPM=(M-2 )/2。

综上，各调制方式的误时隙率可表示为

将式（31）代入到式（32）可得

在不同调制方式进行比较时，一般考虑平均功率相等，不同调制方式的峰值功率与平均功率的关系由它们的调制结构决定。假设发射一个相同符号的平均功率为P，则OOK 的峰值功率Pt，OOK=2P，同理可得其他几种调制方式的峰值功率分别为Pt，LPPM=2nP、Pt，DPPM=(2n+1 )P/2、Pt，NDPPM=(2n-1+3 )P/3、Pt，MPPM=MP/k。

由前文分析的平均接收光功率与光强的关系Pr=Ar⋅I，并根据式（18）平均信噪比μ0的定义，将各调制方式的误时隙率化简为平均信噪比形式，可得

式中，r的定义如前所述，c定义为各调制方式峰值功率与平均功率的比值，分别为cOOK=2、cLPPM=2n、cDPPM=(2n+1 )/2、cNDPPM=(2n-1+3 )/3、cMPPM=M/k。

将式（34）和式（19）代入式（22），可得Gamma-Gamma 湍流信道下系统的平均误时隙率为

DPPM 和NDPPM 符号长度不固定，如果一个时隙发生错误，可能会影响后面符号的判决，所以常用误包率来比较各种调制方式的差错性能。假定只要检测到一个包中有一个时隙有错误，则认为整个包出错。设一个包含有N比特信息，采用每符号n比特方式调制，则每个包含有的符号数为N/n，误包率定义为［4］

式中，Lav为平均符号长度，不同调制方式的平均符号长度不同，分别为Lav，OOK=n、Lav，LPPM=2n、Lav，DPPM=(2n+1 )/2、Lav，NDPPM=(2n-1+3 )/2、Lav，MPPM=M。

将式（35）代入式（36），可得Gamma-Gamma 湍流信道下系统的误包率为

式中，不同调制方式的r、c和Lav不同，定义如前所述。

4 数值仿真与分析

为了分析系统和信道参数对FSO 通信系统性能的影响，基于上述推导的Gamma-Gamma 湍流信道下的误包率表达式进行仿真。为便于后续实验验证，激光波长选取1 550 nm 波段，接收天线选用卡塞格林结构，考虑到接收增益、激光束散角、接收视场及光端机体积重量，接收孔径选用0.08 m。分析湍流强度对系统性能影响时，大气折射率结构常数取了三个不同的值，分别为9.0×10-15m-2/3、4.0×10-14m-2/3、1.0×10-13m-2/3，对应弱、中、强三种湍流；分析传输距离对系统性能影响时，L取了三个不同的值，分别为1 500 m、2 200 m、3 000 m；分析调制阶数对系统性能影响时，n取了五个不同的值，分别为3、4、5、6、7。仿真参数名称及取值如表2。

表2 仿真参数Table 2 Simulation parameters

图6 为调制阶数n=5，三种湍流强度条件下，不同传输距离的NDPPM 系统的误包率与信噪比的关系曲线。由图6 可知，误包率曲线均随信噪比的增加呈下降趋势。当距离一定时，误包率随着湍流强度的增大而增大，如在L=1 500 m、、信噪比μ0=12 dB 时，误包率约10-6；当湍流增大到时，误包率约10-4，增加了两个数量级。当湍流强度一定时，误包率随着距离的增加而增大，如在、L=2 200 m、信噪比μ0=14 dB 时，误包率约为10-7；当传输距离增加为L=3 000 m 时，误包率约为10-5，增加了2 个数量级。但不同湍流强度下，传输距离的变化对误包率性能的影响程度不同，可以发现，在强湍流下，传输距离的变化对误包率性能影响小；而在弱湍流和中等湍流时，传输距离的变化对误包率性能影响较大，如在信噪比μ0=14 dB，弱湍流（）下，传输距离由2 200 m 增加到3 000 m 时，误包率增加了2 个数量级；而强湍流（）下，同样距离的变化，对应的误包率仅增加了不到一个数量级。出现上述现象的原因是：当湍流较强时，湍流是影响误包率性能的主要因素，而在弱、中湍流下，传输距离的变化是影响误包率性能的主要因素。因此，当传输距离增加时，若要保证系统性能不变，则需要根据不同强度湍流条件提高相应的信噪比。

图6 不同湍流强度、不同传输距离下NDPPM 的误包率与信噪比的关系Fig.6 Packet error rate vs SNR of NDPPM with different turbulence intensities and transmission distances

图7 不同调制阶数下，NDPPM 的误包率与信噪比的关系Fig.7 Packet error rate vs SNR of NDPPM with different modulation orders

图8～10 为传输距离L=2 200 m，三种不同强度湍流条件下，五种不同调制方式的误包率与信噪比的关系曲线。其中图8 为弱湍流（）条件下各调制方式的误包率比较，图8（a）中n=5，图8（b）中n=7；图9 为中等强度湍流（）条件下各调制方式的误包率比较，图9（a）中n=5，图9（b）中n=7；图10 为强湍流（）条件下各调制方式的误包率比较，图10（a）中n=5，图10（b）中n=7。由图8～10 可知，随着信噪比的增加，各调制方式的误包率均减小。相同调制阶数下，随着湍流强度的增大，各调制方式的误包率均增大；弱湍流条件下，若误包率为10-6，各调制方式的误包率性能明显优于中等湍流条件下（约优于3 dB）和强湍流条件下（约优于4 dB）。湍流强度、调制阶数一定时，在相同信噪比下，NDPPM 的误包率性能不如DPPM，但可采用更高的调制阶数来获取更优的性能，由图8（a）和图8（b）可知，在μ0=10 dB 时，n=7 的NDPPM 误包率（约10-5）比n=5 的DPPM 误包率（10-4）小了1 个数量级；NDPPM 的误包率性能明显优于MPPM 和OOK，由图8（a）、图9（a）和图10（a）可知，当n=5，误包率为10-6时，NDPPM 的误包率性能在弱、中、强湍流条件下分别优于MPPM 约1.57 dB、1.52 dB、1.5 dB，分别优于OOK 约4.72 dB、4.65 dB、4.6 dB；由图8（b）、图9（b）和图10（b）可知，当n=7，误包率为10-6时，NDPPM 的误包率性能在弱、中、强湍流条件下分别优于MPPM 约4 dB、3.95 dB、3.91 dB，分别优于OOK 约10 dB、9.93 dB、9.9 dB。因此，随着调制阶数的增大，NDPPM 的误包率性能优于MPPM 和OOK 越明显。对比图8、图9 和图10 可以发现，在湍流强度一定条件下，OOK 的误包率不受调制阶数的影响，即改变其调制阶数并不能改善其差错性能。几种PPM 方式的误包率均随着调制阶数的增大而减小，因此，可以通过增大调制阶数来改善PPM 系统的差错性能。

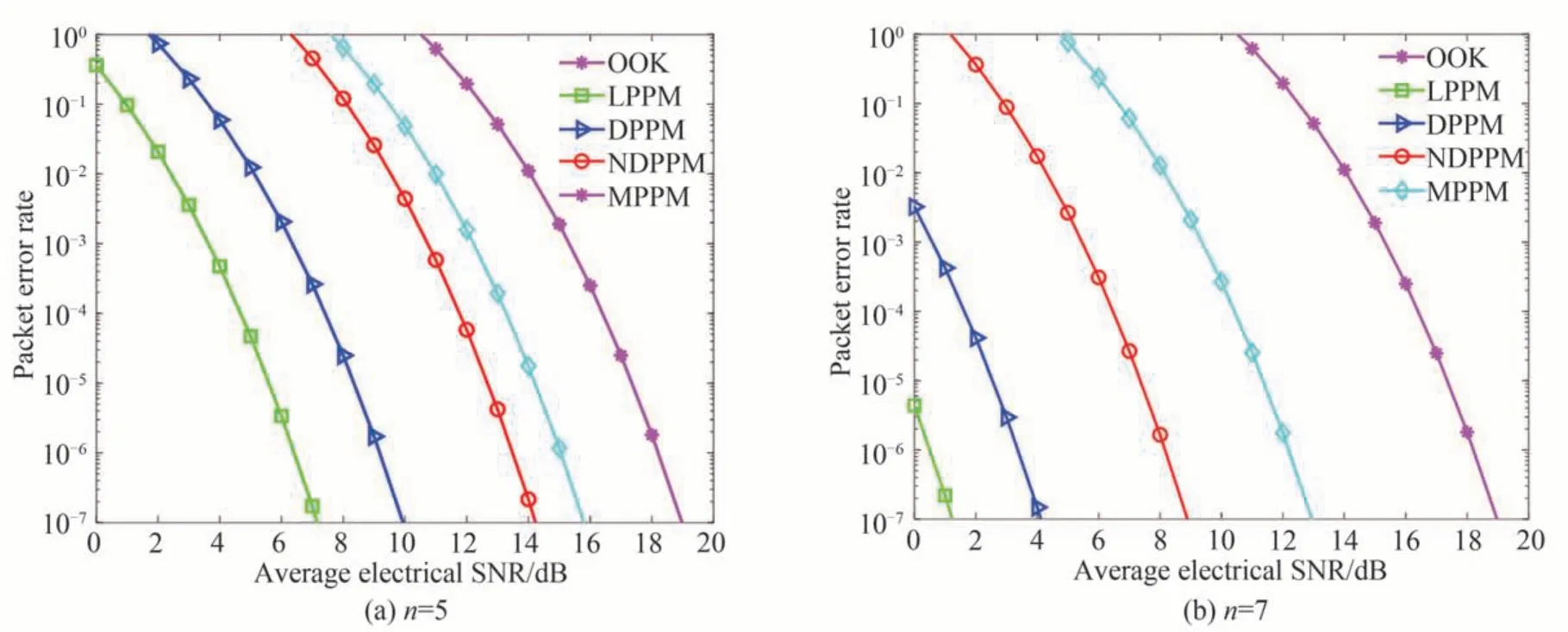
图8 弱湍流（）下，各调制方式的误包率比较Fig.8 Comparison of packet error rate of various modulation schemes under weak turbulence

图9 中等强度湍流（）下，各调制方式的误包率比较Fig.9 Comparison of packet error rate of various modulation schemes under medium turbulence

图10 强湍流（）下，各调制方式的误包率比较Fig.10 Comparison of packet error rate of various modulation schemes under strong turbulence

5 结论

本文提出一种新型脉冲位置调制方式，即NDPPM。研究并分析了其调制性能，推导出Gamma-Gamma湍流信道下FSO 通信系统的平均误时隙率及误包率模型，仿真分析了湍流强度、传输距离和调制阶数对NDPPM 系统性能的影响，并与其他几种调制方式进行了比较。理论分析和仿真结果表明：与传统PPM 方式相比，NDPPM 的传输容量最高，同时其带宽需求较低，仅次于MPPM，但传输容量、功率利用率和差错性能上均优于MPPM，并且相比于MPPM，NDPPM 不需要符号同步，可简化系统实现的复杂度。NDPPM 的差错性能虽不如DPPM，但可采用更高的调制阶数来获取更优的性能，其传输容量是DPPM 的2 倍，带宽需求仅为DPPM 的一半（n≥6）；其差错性能明显优于MPPM 和OOK，在误包率为10-6时，其性能优于MPPM和OOK 分别为4 dB 和10 dB（），并随着调制阶数的增大，性能优势越明显。由NDPPM 系统和信道参数仿真可知，湍流强度的增大或传输距离的增大，会导致NDPPM 系统性能降低，但不同湍流强度下，传输距离的变化对误包率性能的影响程度不同；弱、中湍流条件下，传输距离的变化对误包率性能影响较大。调制阶数增大或信噪比增大，均可提升NDPPM 系统性能，在误包率为10-6时，调制阶数每增加1 可至少节省2 dB 信噪比（）。各调制方式没有绝对的好与坏，评价一种调制方式是否有优势必须针对其应用场合，在实际FSO 通信中可以根据需求偏重其中某个方面，从而选择合适的调制方式。因此，从系统实现的复杂度及性能综合考虑，NDPPM 在FSO 通信中具有一定的优势和应用场合。在实际应用中，可以利用推导的模型，估计系统性能，为FSO 通信系统设计提供参考。