结构光照明光切片显微图像的高保真重构方法
谢贤峰,千佳,李星,党诗沛,柏晨,闵俊伟,但旦,姚保利
(1 中国科学院西安光学精密机械研究所 瞬态光学与光子技术国家重点实验室,西安 710119)
(2 中国科学院大学,北京 100049)
0 引言
生命科学的发展需要对生物的微观结构分布和形态特征进行全面观察。光学显微镜因其低损伤和实时成像的优势成为生物研究的有力工具[1-2]。然而,由于成像景深的限制,传统光学显微镜不具备三维显微成像的能力。景深范围内的光线聚焦形成目标像,而景深范围外的光线散焦形成背景,两者混合在一起,形成一个二维强度图像,两个部分彼此难以区分,影响对目标的精确识别[3]。要解决这一问题,关键是如何从离焦背景中分离出在焦目标。目前已有许多技术可以解决此问题,如激光扫描共聚焦显微术(Laser Scanning Confocal Microscopy,LSCM)[4-5]、光片荧光显微术(Light Sheet Fluorescence Microscopy,LSFM)[6-8]、光切片结构光照明显微术(Optical Sectioning Structured Illumination Microscopy,OS-SIM)[9-12]等。其中,OS-SIM技术由于其结构简单、成像速度快、兼容性好等优点,非常适合应用于生物医学和材料科学等领域。
1997 年,NEIL M A A 等[13]提出了SIM 显微术的概念,用于消除宽场显微镜中的离焦背景,从而获得光切片图像。当具有一定频率的空间条纹图案投射到物体上时,只有在焦平面区域的物体才可以承载条纹,而离焦区域则不受条纹图案影响。通过对三种不同相位结构光场照明下的图像进行简单处理,即可提取光切片图像[14]。在光切片重构算法方面,由NEILM A A 等提出的均方根(Root Mean Square,RMS)算法在大多数情况下仍然被使用。然而,该算法也有一些缺点。RMS 算法在低信噪比和低条纹对比度的情况下,重构出的光切片图像往往信噪比较低,甚至出现残留条纹。对于生物荧光样品,大多数时候荧光信号很微弱,背景噪声较高,使得RMS 算法的处理结果往往不够理想。为了弥补RMS 算法的不足,一些改进的重建算法相继被提出。2014 年PATORSKI K 等[15]提出了一种基于二维希尔伯特变换的FABMED-HS(Fast and Adaptive Bi-Dimensional Empirical Mode Decomposition-Hilbert Spiral Transform)算法。该方法在运算过程中进行了选择性的滤波,可以在一定程度上去除光切片图像中的噪声,但需要对图像进行复杂的二维经验模态分解和希尔伯特变换。之后,2015 年ZHOU Xing 等[16]提出了一种基于一维希尔伯特变换的SHT(Sequence Hilbert Transform)算法,大大简化了处理流程,但该方法没有涉及噪声相关的操作,在噪声抑制方面表现不佳。2020 年DANG Shipei 等[17]提出一种Fourier-OS-SIM 算法,该算法在频域上对图像进行处理,可以使用多种滤波器抑制背景噪声,提高图像重构质量,但在频域的运算相对复杂,处理速度相对较慢。
本文从理论上分析并推导出了一种新的光切片算法:标准差(STandard Deviation,STD)算法,该算法结合了去背景和去卷积处理。去背景处理可以解决由于背景荧光过强导致条纹对比度较低的问题,去卷积处理可以消除系统点扩散函数对成像的影响。与传统的RMS 算法相比,STD 算法不仅可以实现光切片重构,还可以增强图像中微小细节的可见性。设计并搭建了一套基于数字微镜器件(Digital Micro-mirror Device,DMD)的结构照明显微成像系统,并在该系统上进行了一系列生物样品的光切片实验,通过与传统RMS 算法的对比,证明了STD 算法的优点和有效性。
1 理论分析
1.1 RMS 算法存在的问题
RMS 算法在推导过程中使用了两个近似:第一个是认为背景强度在成像过程中是近似不变的,可以通过两两之间相减的方法消去;第二个是近似认为系统点扩散函数对图像采集没有影响。当图像信噪比和条纹对比度都较高时,这两个近似对光切片重构影响不大。然而,在弱荧光显微的情况下,这两个近似带来的影响就会变得明显,这也是RMS 算法重构出的结果信噪比低,往往会灰度值缺失的原因。图1 展示了使用Nikon 40×/NA0.75 的显微物镜,以小鼠肾脏细胞为样品,得到的宽场图像和RMS 算法重构的结构光照明光切片图像。从图中可以看出,RMS 算法重构的光切片图像中出现了许多残留条纹和噪点,这些缺陷掩盖了图像中的一些细节。

图1 小鼠肾脏细胞的宽场图像及RMS 算法重构的SIM 光切片图像Fig.1 Wide-field image and RMS reconstructed SIM optical sectioning image of mouse kidney cells
1.2 STD 算法的数理基础
STD 算法的流程可分为五个部分:结构光照明的生成和相移、阵列数码相机捕获荧光图像、对获取的荧光图像进行去背景处理、对去背景后的图像进行去卷积处理、光切片图像重建。该流程如图2 所示。
在OS-SIM 技术中,照明光源发出的照明光经由空间光调制器(Spatial Light Modulator,SLM)或DMD 等光场调制器件调制后,经过显微物镜在样品上形成强度满足一维余弦函数分布的结构光场。该结构光场可以表示为
式中,I0为结构光场的光强平均值,m为条纹的调制度。k0和φ0分别为条纹的空间频率和初相位。通过控制光场调制器件可以在样品上产生任意的结构光场,在OS-SIM 中,往往采用等间隔三步相移的余弦条纹光场。在荧光线性激发响应的情况下,结构光场照亮并激发样品产生荧光信号,这些信号经显微系统成像后,在显微成像系统的像面上,通过数字相机CMOS 或CCD 记录三幅荧光图像,记为D1(x′,y′)、D2(x′,y′)和D3(x′,y′),其中x′和y′表示像平面上的二维图像坐标。由于结构光场只调制在焦分量Din(x,y),对离焦分量Dout(x,y)没有影响,同时考虑到物体表面成像到数码相机CMOS 或CCD 的过程,该过程可以认为是结构光场照明下的成像结果与系统点扩散函数的卷积。结合式(1),此成像过程可以表示为
式中,x和y表示物平面上的二维图像坐标,PSF 表示系统的点扩散函数,⊗表示卷积运算。
由于背景荧光和噪声的干扰,获得的荧光图像信噪比和条纹对比度往往较差,这会给后续的重构算法带来很大压力。如果预先能够从图像中消除一部分背景荧光,则可以提高条纹对比度,从而缓解上述压力,该过程可以用式(3)表示。目前已经有很多方法可以实现此过程,比如使用深度学习的方法去除背景荧光[18],但这需要大量的时间和数据进行训练,以确保它可以处理各种各样的图像。本文使用的是“滚球法(Rolling Ball)”方法[19-20]。该方法模拟了一个虚拟的球沿着图像的强度曲线滚动,将滚球中心位置连接起来就是图像的背景强度,将图像的强度曲线与图像的背景强度曲线相减,就可以达到去背景的目的。
在成像过程中,系统的点扩散函数会对图像进行调制,使点物不能形成点像,而是形成一个弥散斑,影响最终的成像效果。为此,在STD 算法中,加入去卷积运算来消除这种影响。目前有许多流行的去卷积算法都可以实现该功能,如Wiener 滤波算法[21-22]、盲去卷积算法[23-24]和Lucy-Richardson 算法[25-26]。本文选用的是针对显微图像普适性较好的Lucy-Richardson 算法。对式(3)进行去卷积运算后,可得
式中,D′1(x,y)、D′2(x,y)和D′3(x,y)分别是经过去背景和去卷积处理后的三步相移图像。求解式(4)中的Din(x,y),可得
这就是需要的光切片图像。因为式(5)形似标准差公式,所以将该方法称为“STD”。其中,m和I0为常数,取值由结构光场的参数决定,DWF是式(4)中三幅图像的均值,即宽场图像。
2 成像实验
2.1 实验光路
为了验证STD 算法的性能,搭建了一套基于DMD 的结构光显微成像系统,光路设计如图3。光源采用激光二极管照明光源(Laser Diode Illuminator,LDI)(LDI-7,89NORTH Inc.),通过液体光导提供七个波长通道的照明,既可以保证照明光有良好的单色性和准直性,也避免了散斑噪声对成像的影响。光源发出的光束通过准直透镜(Lens 1,焦距30 mm)准直,然后通过全内反射(Total Internal Reflection,TIR)棱镜耦合进入DMD(1 920×1 080 像素,像元尺寸7.56 μm)。TIR 棱镜基于全反射原理设计,可以保证较高的光能利用率,其原理示意如图3(b)。光束首先通过TIR 棱镜入射到DMD 芯片上,然后被DMD 上加载的条纹调制,最后通过TIR 棱镜射出。TIR 棱镜与DMD 的组合使用,既可以满足DMD 特殊的24°入射角,又大大缩短了光路长度,使系统更加紧凑。然后经调制的结构光由Lens 2(焦距300 mm)收集后,进入到Dove 棱镜(PS994M,Thorlabs Inc.)中进行旋转。由于DMD 特殊的偏转角度,调制光斑是旋转倾斜的,使用Dove 棱镜的旋像功能可以使获得的图像旋转成水平方向,便于相机采集图像。结构光从Dove 棱镜出射后,经二向色镜(490 nm 长通,DMLP490,Thorlabs Inc.)反射进入显微物镜,最终在样品焦面上汇聚。样品激发的荧光通过显微物镜返回,再次通过二向色镜,经过滤光片(FL-004532,Semorock Inc.)滤除照明光和环境光后,使用筒镜收集,最后在sCMOS 相机(ORCA-flash4.0,Hamamatsu Inc.)上采集荧光图像。在三维成像过程中,利用电动位移工作台(P-725,Physik Instrumente Inc.)在z轴上移动样品,可获得样品不同深度位置的图像数据,经过后期数据处理和整合后可获得样品的三维图像。
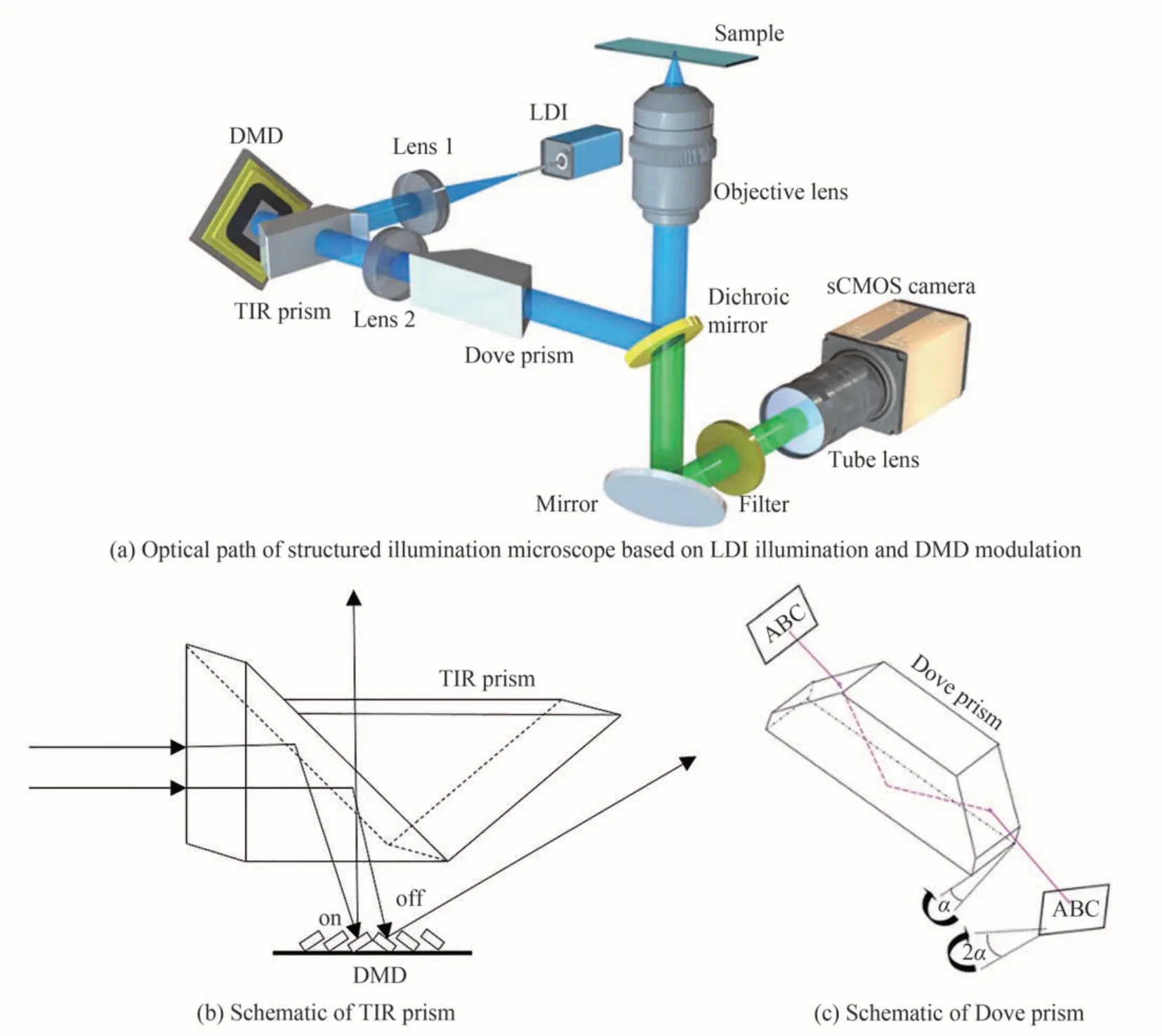
图3 实验光路Fig.3 Experimental optical path
2.2 实验结果与分析
2.2.1 STD 算法和RMS 算法的成像对比
为了比较STD 算法和RMS 算法在光切片上的差异,基于上述系统对小鼠肾脏细胞和牛肺动脉内皮(Bovine Pulmonary Artery Endothelial,BPAE)细胞进行了成像实验。首先以小鼠肾脏细胞为样品,照明光波长为470 nm,显微物镜为Nikon 40×/NA0.75 物镜。利用sCMOS 相机获取了三幅具有2π/3 等间距相移、横向条纹周期为1.35 μm 的原始图像,然后分别使用RMS 算法和STD 算法进行重建。图4 为小鼠肾脏细胞成像结果。从图4(d)~(f)和(g)~(i)中可以看出,RMS 算法和STD 算法都可以实现光切片的功能。但与STD 算法相比,RMS 处理结果中存在较严重的噪声和残余条纹,严重影响了光学切片图像的质量。从结果可以看出,STD 算法可以有效地抑制噪声,消除残余条纹,提高成像质量。从图4(j)中的归一化强度曲线可以看出,STD 算法使图像的背景强度更低,对比度更高。

为了进一步验证STD 算法的优越性,用同样的显微物镜对BPAE 细胞进行了成像实验。照明光波长依然为470 nm,二向色镜和滤光片型号保持不变。与之前不同的是,本次实验的条纹对比度很低(小于0.1)。结果如图5。从图中可以看出,STD 算法的重构结果中仍然具有更低的噪声,更好的图像对比度和更精细的微观结构。相比之下,RMS 算法的处理结果几乎被噪声淹没。从图5(j)还可以看出,RMS 重构图像对应的曲线中有更多“毛刺”,而宽场图像和STD 重构图像中几乎没有,这是由图像中的噪声引起的。这些“毛刺”严重影响光切片的质量。这说明当条纹对比度较低时,RMS 算法的重构结果并不理想,而STD 算法仍然可以获得较为理想的光切片图像。


图5 低条纹对比度时不同算法重构牛肺动脉内皮细胞的成像结果对比Fig.5 Comparison of imaging results reconstructed by RMS and STD algorithms for BPAE cells under low contrast structured illumination
2.2.2 与以前数据的重构结果对比
STD 算法具有普适性,为了验证这一点将其应用于以前采集的数据中,同样得到了比RMS 算法更好的光切片图像,如图6。样品为螨虫样本,显微物镜为Nikon 20×/NA0.45 物镜。由于螨虫样本较厚,在宽场图像中,清晰的在焦部分和模糊的离焦部分糅合在一起,没有明显的区分,而在光切片图像中可以看出在焦部分和离焦部分有着明显的区分。对比图6(b)和6(c)可以发现,RMS 算法和STD 算法都可以实现光切片,但RMS 算法重构结果中有着明显的噪点,掩盖了图像中的一些细节结构。STD 算法的重构结果中没有明显噪声,样本中的细节结构依然清晰可见,说明STD 算法有更加优秀的光切片重构能力。

图6 使用RMS 算法和STD 算法重建螨虫样本的成像结果对比Fig.6 Comparison of imaging results reconstructed by RMS and STD algorithms for mite sample
2.2.3 双波长通道光切片
实验中发现改变照明波长对成像位置的影响很小,这使得多波长的光切片成为可能。使用两种波长的光照明小鼠肾脏细胞,显微物镜仍为Nikon 40×/NA0.75 物镜。首先使用波长为470 nm 的光束照明样品,图像采集完成后,将光源波长切换为555 nm,更换相应的二向色镜(567 nm 长通,DMLP567,Thorlabs Inc.),继续采集图像。最后两组原始图像分别处理后叠加,即可获得双波长激发下的融合重构图像,结果如图7。该样品使用不同的荧光分子标记细胞中的不同结构,因此在不同波长的光照激发下,能够观测到不同的荧光标记结构,获取更多的结构信息,有利于对样品的全面观察。从图7 中可以看出,在双波长光源照明下,STD 依然具有良好的光切片效果。

图7 双波长照明激发下小鼠肾脏细胞的成像结果Fig.7 Imaging results of mouse kidney cells under dual wavelength illumination
2.2.4 三维显微成像
OS-SIM 的最终目的是实现三维成像,STD 算法能重构出更为理想的光切片图像,使三维成像效果更加真实。如图8,以花粉颗粒为样品进行了三维图像重构。使用的显微物镜放大倍率为20,数值孔径为0.75,切片每层厚度为200 nm,视场大小为163.84 μm×163.84 μm,共采集了125 层。

图8 花粉颗粒的三维成像结果Fig.8 3D image of pollen grains
3 结论
本文在结构光照明光切片成像理论的基础上,提出一种新的光切片图像重构算法:STD 算法。该算法在原始图像信噪比和条纹对比度不高时仍然可以获得理想的光切片图像。从理论上对STD 算法进行了推导,对STD 算法的流程进行了说明。搭建了一套基于DMD 的结构照明显微成像系统,利用该系统分别对小鼠肾脏细胞、牛肺动脉内皮细胞等样品进行了OS-SIM 成像实验。结果表明,STD 算法在重构效果上明显优于传统的RMS 算法,能够有效降低背景噪声、消除残余条纹,实现更精细的光切片成像。STD 算法对其它类型的结构照明光场也具有适用性,这将在后续的工作中开展进一步的研究。

