基于数学本质的几何概念教学有效路径
江苏省南京市文靖东路小学 史伟琴
数学本质是指从数学学科的视角研究数学知识,包括数学知识的来源、发展以及运用。基于数学本质的教学设计,是有效实施数学课堂教学的前提。几何概念能反映几何图形的本质属性,经历了从感性认识到理性认识的抽象过程。那么,如何凸显数学本质,进行几何概念教学设计呢?可以从以下几方面展开。
一、整体视角分析,厘清本质
整体的视角意味着要从多角度分析数学知识,而不是单一地、孤立地看待数学知识。数学知识的本质并不等同于数学教材中的描述与说明。数学教材往往要考虑学生的接受能力,有时会舍去一些严谨性而规范性的表达。同时,数学教材由于篇幅的限制不可能充分展开,只能摘其要点,不会对“是什么”“为什么”“怎么用”等进行完整的叙述。
例如,圆的本质是什么,可以从数学教材中圆的概念部分去解读。在数学教材中,对于“圆”的定义主要采用的是描述性的定义,通过圆的要素半径和直径的特征来帮助学生了解圆这种图形。中学阶段圆基本上给出的是几何定义:平面内到定点的距离等于定长的所有点组成的图形,其中定点和定长分别为该圆的圆心和半径。当然,圆还有其他两种定义说法:一种是轨迹说,另一种是集合说。从几种不同的定义方式,我们能发现小学阶段的圆的定义采用的是静态定义方式,比较直观,利于形成圆的表象;而初中阶段针对圆的定义采用的是动态定义的方式,在运动过程中体现出圆的本质特征,即到定点距离一定的所有点运动形成的曲线图形。
圆的本质是什么,还可以通过数学史去梳理。中国历史上最早提出圆的概念的是墨子。早在2000 年前,《墨经》中就记载了“圆,一中同长也”。
从整体的视角分析意味着要弄清知识的来源、发展与应用,教师可以从数学概念定义本身出发,厘清不同定义的区别和联系,把握数学知识的基本内涵;也可以从数学知识的发展脉络出发,梳理不同历史阶段人们对数学知识的理解,弄清知识的来龙去脉,从而深刻把握知识的本质。
二、创设问题情境,直逼本质
把握了知识的本质,接下来要思考怎样把知识的学术形态转为可为学生可接受的教育形态。知识的教育形态是指将知识融入适当的问题情境中,让学生基于情境进行学习。这种问题情境往往基于学生的数学现实,蕴含着数学知识的原型,同时又带有一定的问题意识,可以激发学生强烈的探究欲,引发认知冲突。
如在苏教版数学五年级“圆的认识”一课的教学设计中,为了凸显圆的动态定义这一核心知识,笔者创设了一个具有探究性的问题情境:同学们将要进行一个游戏活动——套圈。至少3 个同学做套圈游戏,怎样站立才公平?套圈的位置可以用一个圆点表示,玩家的人数可以是3 人、4 人,甚至更多的人。明白了吗?出示学习单(如图1),学生自主思考。
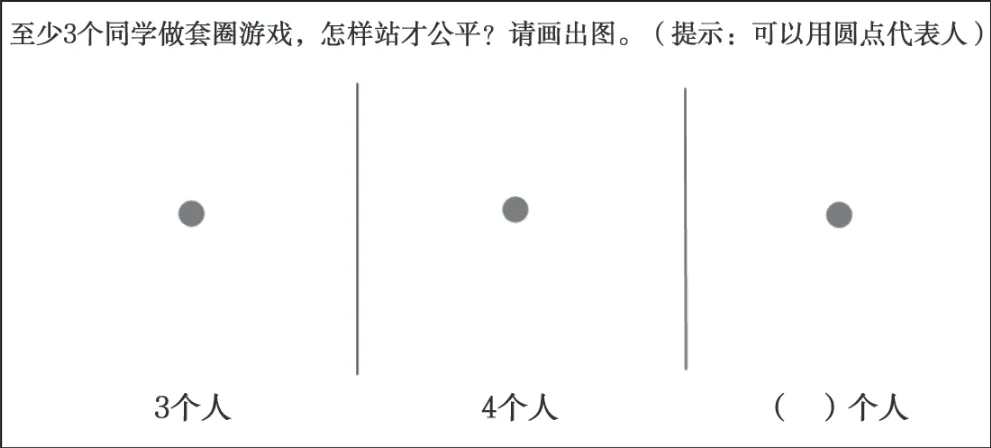
图1
在“套圈游戏”的情境中,蕴含着一个问题:怎样站才公平。这一情境的创设从套圈游戏到怎样站才公平,有意识地引导学生学会从数学角度发现和提出问题。“怎样站才公平”这一问题助推学生主动参与数学活动,积极探索新知。学生在自主探究过程中形成的活动经验也是进一步学习的基础。由此,学习不断深入,直至问题解决。在解决问题的过程中,学生能感悟到圆的本质,即到定点距离定长的点的集合,从而进一步理解“圆,一中同长也”。合理的问题情境不仅可以凸显数学知识的本质,还要设法让学生“卷入”探究过程中。
三、经历数学化过程,形成本质
弗赖登塔尔认为,学生学习数学是一种“数学化”的过程。数学化就是数学地组织现实世界的过程。这里的“数学化”过程不能仅仅依靠教师的灌输,更重要的是学生自我的建构,让学生尝试用自己的方式表达对数学的理解,建立数学知识之间的内在联系。在此基础上,不同思维层次的学生通过互动交流,不断纠错,不断完善,才能实现感性经验向理性知识的跃升,完成感性经验向数学知识的转化。
如在教学“圆的认识”一课时,教师创设了“套圈游戏”的问题情境后,组织学生交流汇报。
【教学片段】
学生交流后,汇总出了5 种不同的方法。
方法1:排成一条直线的。
方法2:排成长方形,人放在顶点。
方法3:摆成正方形,人的位置放在顶点和每条边的中点。
方法4:摆成正三角形、正多边形的,人放在顶点。
方法5:放在一段弧上的。
师:同学们真爱动脑筋,想出了这么多方案。这些方案有什么共同点?看来只要点到中心点的距离相等就可以。
师:如果两个人之间的距离相等,就会形成正三角形;如果四个人呢?人越来越多,会形成什么样的图形?
师:结合刚才的研究,闭上眼睛想象,你认为圆是一个什么样的图形?
生:到中心一样长的无数点就形成一个圆。
本节课中出现了比较有代表性的3 个学生的作品。1 号作品(如图2),学生通过测量或根据已有的知识“点到直线的所有线段中,垂直线段最短”,能够发现这一设计是存在缺陷的,由于每个人到套圈位置的长度不同,游戏是不公平的;2 号作品(如图3),通过精准的测量,展示每个人到套圈位置的距离要相等;3 号作品(如图4),在测量的基础上,又进一步发挥自身的想象,把可能的点的位置描了出来。不同作品体现出学生不同的思维特点,通过课堂中的交流辨析,学生都能领悟到“圆,一中同长”这一本质特征。

图2

图3
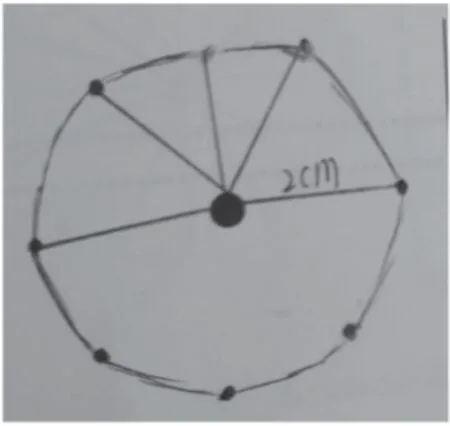
图4
在此基础上,多数学生已经感受到这些点的集合会形成一个圆形。此时,教师设计想象无数点汇集成圆这一环节。圆,作为一个抽象的数学图形,在生活中虽然随处可见其实物模型,但这些都不是真正数学意义上的圆。数学意义上的圆是没有瑕疵的,没有直线的,这些特质只能付诸学生的自我想象。这一环节中想象圆的形成过程是不可缺少的部分,突破圆的实物模型束缚,领悟数学中的圆的本质。
四、感悟数学思想,强化本质
从数学本质出发,不仅要关注数学知识的本质,还要深入分析数学思想。数学可以分成不同的知识板块,知识之间有着联系和区别。如果将数学知识比喻成散落的珍珠,那么数学思想就是将这些珍珠串联起来的金线。解释和分析现实世界的数学知识会不断地更新,但数学基本思想是数学的灵魂。
如在苏教版数学五年级上册“圆的面积”的教学中,教师在引导学生探究圆的面积推导时,就设计了体悟转化这一思想的教学环节。首先,通过回顾学过的长方形、正方形、三角形、梯形等平面图形面积的推导过程,激活学生已有的认知经验,体会转化思想,为圆的面积推导做铺垫。但圆不同于其他直线图形,它是一种曲线图形,那么如何进行分割,将其转化成哪种我们学过的图形来推导它的面积,就成为学生迫切需要思考的问题。对于如何转化圆这一曲面图形这一问题,教师先让学生动手尝试未果后,出示一张生活中常见的比萨图片,学生便恍然大悟,可以从圆心,沿着圆的半径等分圆。
解决了如何分割圆之后,转化成哪种平面图形进行推导?联系已有直线图形的面积推导,学生不仅可以想到转化成平行四边形、长方形,也可以转化成不常见的三角形和梯形。(如图5)
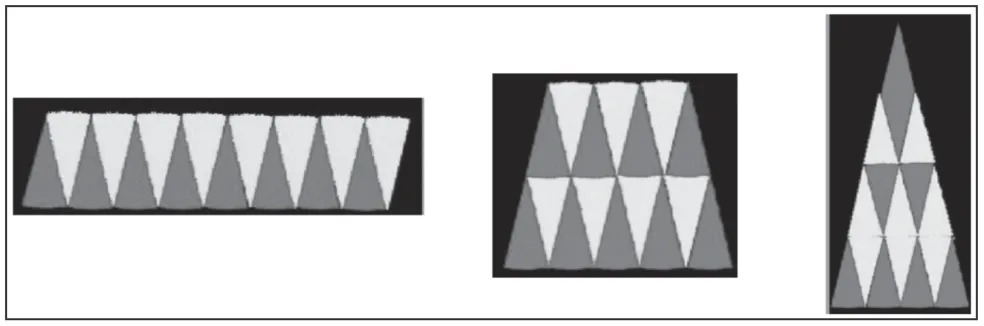
图5
【教学片段】
师:我们通过生活中等分比萨的事例,类比出等分圆的方法。那么,我们需要将圆这一曲线图形转化成哪种学过的平面图形呢?
小组合作,拼一拼,说一说圆的面积推导过程。
生1:我把圆等分16 份后,可以将其转化成平行四边形。平行四边形的底是圆周长的一半,高是圆的半径,底×高就得到平行四边形的面积,也就是圆的面积。
生2:也可以将圆转化成一个梯形来求,上底和下底的长度和就是圆周长的一半,高是圆半径的2 倍,利用梯形面积公式,求出梯形面积,也就是圆的面积。
师:用这些方法虽然将圆转化成不同的平面图形,但有什么相同的地方?
生4:都是将圆转化成我们学过的平面图形,找到转化过后底和高与原来圆的关系,再推导出圆的面积公式。
……
如此体现转化的具体方法的多样化,进一步拓宽学生的思维空间,增强学生思维的灵活性。

