原油蒸馏曲线单调递增指数函数样条插值方法研究
陈 宏,范钦臻,程丽华,梁朝林,谢 颖
(1.广东石油化工学院化学工程学院,广东 茂名 525000;2.劣质油加工广东省普通高校重点实验室)
原油及其馏分油均为复杂的混合物,以现有表征手段尚无法完全分析其详细化学组成。Miquel等[1-2]提出用虚拟组分来表征原油馏分的化学组成,即根据原油或宽馏分油的蒸馏曲线将其切割成若干个馏程较窄的馏分,然后将每个窄馏分油当作一个虚拟组分,从而由虚拟组分的物性计算原油或宽馏分油的物性。
此后,许多学者以虚拟组分法为基础对原油加工过程进行了模拟研究,如部分学者[3-5]以虚拟组分法为基础,对常减压蒸馏装置的流程进行了模拟与优化;还有部分学者[6-9]基于虚拟组分法建立模型,对催化裂化装置的反应-再生系统的动力学参数、动态特性和多稳态特性分别进行了模拟。研究发现[10],基于Braun K10法的图表数据开发的虚拟组分体系气-液平衡常数模型,对实际体系的计算具有较高的可靠性。Bennett等[11]以虚拟组分法为基础建立计算模型,准确预测了烃类与水的互溶性。
虚拟组分法也是ASPEN和SIMSCI PROⅡ等流程模拟软件处理复杂体系的常用方法,其中虚拟组分切割的可靠性取决于原油评价和产品蒸馏曲线的完整性和可靠性。原油及其馏分油的评价一般采用实沸点蒸馏(TBP,依据ASTM D2892标准方法)、模拟蒸馏(依据ASTM D2887标准方法)、减压蒸馏(依据ASTM D1160标准方法)或恩氏蒸馏(依据ASTM D86标准方法)等方法,获得有限个单调递增的蒸馏数据(温度-馏出率)[12]。然而,实际操作中得到的温度-馏出率数据有限且数据区间分布不均匀,无法直接满足虚拟组分法细分馏分的要求,因而需要使用数据补充方法对温度-馏出率数据进行扩展,才能得到完整光滑的蒸馏曲线。常用的数据补充方法有内插法、外推法等,为了保证补充数据与实际油品评价数据一致,选择合适方法来确保补充数据的精度至关重要。
在各种流程模拟软件中,油品馏程数据补充最常用方法是曲线插值法,如二次样条插值法[13]、三次样条插值法等[4,14]。然而,这些插值方法获得的数据虽然一阶导数连续,却无法保证插值结果的单调递增[13]。因此,上述插值方法均不能完全满足补充油品蒸馏数据的要求。
鉴于上述插值方法的不足,本课题基于虚拟组分法,提出一种仅含3个参数的指数函数样条插值方法,并分段构造由3个参数指数函数组成的插值函数,保证插值数据一阶导数连续且递增,满足油品蒸馏曲线连续光滑且递增的要求,从而提高对原油加工过程进行模拟计算的准确度。
1 指数函数插值模型
参考其他插值方法,分别从插值模型的问题描述、边界条件、插值方程求解3个方面说明插值模型的研究方法。
1.1 问题描述
已知试验测得油品的蒸馏曲线在区间[a,b]中互异的n个节点x1,x2,…,xn(a=x1 指数函数样条插值方法:首先,在蒸馏曲线的每个节点小区间[xi,xi+1](i=1,2,…,n-1)中构造指数函数Si(x),使其与蒸馏曲线的馏出温度值y近似,如式(1)所示。 (1) 式中:exp为以自然数e为底的指数函数;abs为求绝对值的函数;Ai,Bi,Ci均为系数,其中Ai为温度系数,℃,Bi、Ci为比例系数,%。 由式(1)取一阶导数得式(2)。 (2) 从式(2)可知,式(1)的插值函数是单调递增的。式(1)中,当Ci>0时,Si(x)为凹函数;当Ci<0时,Si(x)为凸函数。原油蒸馏曲线与双曲正弦曲线相似,即左侧部分为凸函数,右侧部分为凹函数;基于式(1)对原油蒸馏曲线进行分段插值,其形状特征更接近油品实际蒸馏曲线。 为了确保指数函数插值在相邻节点处连续且一阶导数连续,Si(x)应满足约束方程式(3)~式(5)。 Si(xi)=yi,i=1,2,…,n-1 (3) Si(xi+1)=yi+1,i=1,2,…,n-1 (4) S′i(xi)=S′i-1(xi),i=2,3,…,n-1 (5) 由式(3)~式(5)可知,该指数函数样条插值函数共有3n-3个未知数和3n-4个约束方程,因而还需指定1个边界条件才能确定Si(x)。 边界条件的设定是指数函数样条插值方法的关键步骤,决定了样条插值的效果。针对不同类型的曲线,应该研究确定不同的边界条件,才能确保样条插值的准确性。对于原油的蒸馏曲线来说,其在馏出率(xm)为[30%,70%]区间与直线近似。因此,可假设馏出率50%处蒸馏曲线的一阶导数为馏出率30%和70%两点间直线的斜率,即: S′(50)=(t70-t30)/(70-30) (6) 式中,t30、t70分别为蒸馏曲线上馏出率为30%和70%时的馏出温度,℃。 确定S′(xm=50)后,可将蒸馏曲线分成两段(xm≥50%部分为上段,xm<50%部分为下段),然后从xm=50(一般刚好为蒸馏数据点数的一半)点开始,分别向两端依次求解式(3)~式(5)方程组的系数。 1.3.1蒸馏曲线上段指数插值模型系数求解 在区间[xi,xi+1](i=m,m+1,…,n-1)内构造指数函数Si(x),将式(1)代入式(3)~式(5),得到含3个未知数Ai,Bi,Ci的方程组,见式(7)~式(9)。 (7) (8) (9) 由式(9)变换可得: (10) Bi=xi-Ciln[S′i(xi)×abs(Ci)] (11) 将式(10)代入式(7),整理得: Ai=yi-CiS′i(xi) (12) 将式(12)代入式(8),整理得: (13) 将式(13)与式(9)相除,整理得: (14) 式(14)中,根据已知的xi+1,xi,yi+1,yi,S′i(xi),采用牛顿法、割线法等非线性方程求解方法可求得系数Ci,然后再用式(11)、式(12)分别计算得到系数Ai、Bi。 蒸馏曲线上段右端点的一阶导数为: (15) 1.3.2蒸馏曲线下段指数插值模型系数求解 对蒸馏曲线下段区间[xi,xi+1](i=2,3,…,m-1,m),可得到含3个未知数Ai-1,Bi-1,Ci-1的类似方程组,如式(16)~式(18)所示。 (16) (17) (18) 经过相同步骤,可推导得到系数求解方程组,见式(19)~式(22)。 (19) Ai-1=yi-Ci-1S′i-1(xi) (20) Bi-1=xi-Ci-1ln[S′i-1(xi)×abs(Ci-1)] (21) (22) 式(19)~式(22)中,i=2,3,…,m-1,m,其中S′i-1(xi-1)是蒸馏曲线下段左端点的一阶导数。 综上可知,利用式(11)~式(13)、式(15)和式(19)~式(22),可求得原油蒸馏曲线的指数样条插值函数的所有系数。 1.3.3参数Ci正负性判断 采用迭代法求解非线性方程式(14)和式(19)时,若给定的参数Ci初值不正确(正数或负数取值错误),则迭代过程很可能不能收敛。因此,方程求解时,需首先确定参数Ci是正数还是负数。 对式(1)取二阶导数可得: (23) 由式(23)可知:当Ci>0时,S″i(x)>0,则分段插值指数函数Si(x)为凹函数;当Ci<0时,S″i(x)<0,则Si(x)为凸函数。凹凸函数如图1示意。 图1 凹凸函数示意 为了直观起见,假设线段AB的斜率为S′AB,凸曲线ACB在A、B两点的斜率分别为S′CA、S′CB,凹曲线ADB在A、B两点的斜率分别为S′DA、S′DB。从图1可以看出,对左侧端点A,凸曲线S′CA>S′AB,凹曲线S′DA 根据上述推导结果,编写了Excel VBA程序。为了验证该指数函数样条插值方法在原油实沸点蒸馏数据插值应用中的准确度,对2012年以来检测的52种原油实沸点蒸馏数据,分别采用三次样条插值法和指数函数样条插值法进行插值计算,并分别计算两种方法的插值与校验值拟合的相关系数,以获得其插值准确度,并判断其是否具有单调递增性质。 以撒哈拉混合原油-2016为例,其实沸点蒸馏数据如表2所示。 表2 撒哈拉混合原油-2016的实沸点蒸馏结果 其插值计算过程如下: (1)在该原油的生产过程中,多数情况下仅测定原油馏出率为0(或5%),10%,30%,50%,70%,90%,100%(或95%)时的馏出温度。因此,在进行插值(内插法)效果检验时,从原油实沸点蒸馏数据中取接近上述馏出率的数据作为插值的已知点,其余数据作为插值结果的校验点。 (2)取馏出率为7.109%,20.353%,36.381%,50.056%,64.881%,89.292%,99.998%的7组蒸馏数据作为插值的已知点,将其余实沸点蒸馏数据作为校验点,分别用三次样条插值方法和指数函数样条插值方法进行插值计算,对比插值结果与校验值的误差,结果如图2所示。 图2 撒哈拉混合原油-2016三次样条和指数函数样条插值结果对比 (3)将三次样条插值和指数样条插值计算结果分别与校验值对比,计算其决定系数(R2)以验证其插值准确度。 (4)将表2实沸点蒸馏数据中最小馏出率与最大馏出率间划分为40等分,以每一个切割点为插值点,分别用三次样条和指数函数样条插值计算,验证插值后馏出率对应的馏出温度是否单调递增,结果见图2。 从图2(a)可以看出,三次样条插值结果在个别点与校验值差别较大,而指数样条插值结果的误差比三次样条插值结果更小。计算插值结果与校验值的拟合决定系数可知,三次样条插值结果的R12=0.805 5,指数函数样条插值结果的R22=0.908 5,可见R22比R12明显增大,说明指数函数插值结果准确度更高。 从图2(b)可以看出:三次样条插值结果不能保证插值结果单调递增,当馏出率从70%增至80%时,馏出温度不升反降,不符合油品蒸馏数据单调递增的规律;指数函数插值结果有效保持了单调递增的趋势。 采用类似的方法,分别对52种原油实沸点蒸馏数据中的其他51种原油蒸馏数据进行三次样条插值和指数函数样条插值对比,其插值结果见表3。 表3 部分原油实沸点蒸馏数据内插结果 从表3可以看出,指数函数样条插值结果准确度高于三次样条插值结果的有50种,占比96.2%;在三次样条插值结果中,有16种原油插值数据无法保持单调递增,占比30.8%;而52种原油的指数函数样条插值结果全部保持单调递增,与理论分析结果一致。 52种原油插值结果与校验值的拟合决定系数如图3所示。从图3可以看出:在三次样条插值结果中,R2>0.99的有21种,占比40.4%;在指数函数样条插值结果中,R2>0.99的有37种,占比71.2%。三次样条插值结果决定系数小于0.9的有6种,而指数函数插值结果决定系数小于0.9的仅有1种。可见,对大多数原油的实沸点蒸馏数据来说,指数函数插值结果的决定系数大于三次样条插值。因此,用于原油实沸点蒸馏数据插值时,指数函数样条插值方法优于三次样条插值法,而且绝大多数(98.1%)指数函数插值结果与校验值的拟合决定系数大于0.9,说明指数函数插值结果更加准确。 图3 两种插值方法决定系数对比 在进行原油加工过程计算时,采用优选方法对有限原油蒸馏数据进行插值补充,是获得单调递增连续光滑蒸馏曲线的基础。鉴于传统插值方法性能的不足,本研究设计了一种仅包含3个参数的指数函数插值方法,在保证计算精准度的同时简化了计算过程。 该指数函数插值法采用分段插值,其形状特征更接近油品实际蒸馏曲线。采用迭代法求解该指数函数的非线性方程时,明确参数Ci是正数还是负数至关重要,若参数Ci初值的正负性不正确,则迭代过程可能无法收敛。 对52种原油实沸点蒸馏数据的插值验证结果表明:采用指数函数插值法能够保证插值后的原油蒸馏曲线单调递增;52种原油的插值结果中,指数函数插值与校验值拟合决定系数(R2)大于0.99的有37种,占比71.2%,三次样条插值结果R2>0.99的仅有21种,占比40.4%;而指数函数插值结果的准确度高于三次样条插值结果的有50种,说明指数函数插值方法效果明显优于三次样条插值方法。1.2 边界条件
1.3 插值方程求解

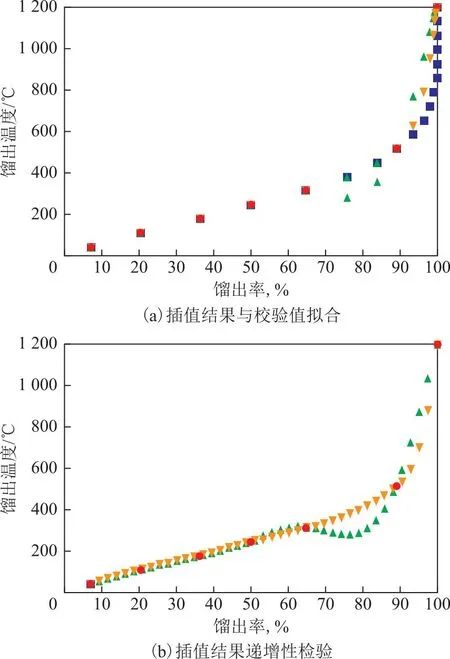
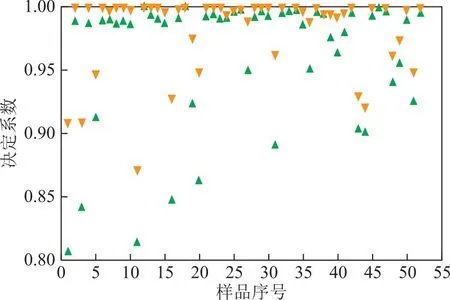
2 指数函数插值效果验证

3 结 论

