石化企业循环冷却水系统腐蚀结垢预测模型的研究

翁新龙，焦云强，欧阳福生，王建平，邸雪梅

(1.华东理工大学化工学院石油加工研究所，上海 200237；2.石化盈科信息技术有限责任公司)

在石化企业中,循环冷却水系统的腐蚀、结垢等问题严重影响生产装置的正常运行,造成经济损失和水资源浪费[1]。针对冷却水系统腐蚀与结垢问题的处理,主要是根据经验通过向循环冷却水系统中投加阻垢缓蚀剂、杀菌剂等药剂来控制腐蚀和结垢。然而,该方法目前还不能根据水质指标的变化动态地调整药剂用量,一方面可能导致药剂浪费,另一方面无法实时应对水质异常变化。判断循环冷却水系统腐蚀、结垢趋势的主要方法有挂片失重法与监测测试法[2]。其中,挂片失重法的采样周期较长,一般需要1个月以上;监测测试法以采用探头监测为主,受水质影响其探头极易损坏,维修成本高昂。因此,通过上述方法均较难获得足够判断系统腐蚀、结垢趋势的有效数据。为了提高数据利用水平、准确判断循环冷却水系统的腐蚀、结垢状况,亟待建立一套低成本、快速响应的循环水腐蚀、结垢预测模型。

某石化企业对循环冷却水系统腐蚀、结垢判断完全依赖现场操作经验,王铁强等[3]为克服这一弊端,运用Matlab建立了预测该系统循环冷却水水质的NARX神经网络模型。机器学习算法的数据处理能力强,是建立数据驱动模型必不可少的工具。喻西崇等[4]采用Cvda-84规范、BP神经网络、改进的Rumelhart方法和MBP神经网络4种不同方法分别对注水管道腐蚀速率进行了预测。曹生现等[5]基于粒子群算法(PSO)的小波神经网络(WNN)建立了换热器污垢热阻和腐蚀速率的在线预测模型。李荣等[6]针对动态水质的预测,提出了一种基于遗传算法改进的网络模型方法。李超等[2]基于软测量技术以及腐蚀结垢研究,设计研发了一套循环水腐蚀结垢在线预测系统。

然而,以上模型建模变量的选取多是依据操作经验,缺少理论依据;而且,其预测结果的平均相对误差(MAPE)均在10%以上、甚至高达20%以上,预测效果欠佳。模型建模变量的选取与模型预测的准确性密切相关,为了提高模型预测的准确性和鲁棒性,本研究基于某石化企业循环水系统的大量基础水质数据,在有效监控关键指标的基础上,采用最大互信息系数(MIC)[7]、Pearson相关系数[8]法在14个水质指标中寻找具有代表性和独立性的参数作为建模变量,通过BP神经网络、KNN回归和极端梯度提升(XGBoost)等机器学习算法建立循环水系统黏附速率和腐蚀速率的预测模型,对循环水系统可能出现的异常情况进行预测预警。

1 数据处理与变量优化

1.1 数据采集与预处理

从某石化企业实验室信息管理系统(LIMS)中采集了2020年1月至2022年12月的24个月循环冷却水水质指标,共计1 015组数据。受现场因素的影响,取得的原始水质分析数据往往存在各种问题,需要进行预处理,剔除噪声大、存在较大偏差的数据,并根据工作经验删除部分不符合实际情况的数据;同时,结合LIMS系统历史样本的分布区间及其水质标准,运用箱线图[9-10]检测各水质指标的异常值(设定异常值范围在箱线图内限之外),对出现无效值、缺失值或离群值过多的变量予以删除或进行异常值替换。

经过数据预处理,保留了899组数据样本以及14个水质性质指标:钙含量、化学耗氧量(COD)、氯含量、总磷含量、游离氯浓度、正磷含量、锌离子浓度、浊度、总碱度、氨氮含量、pH、电导率、腐蚀速率(FSSL)和黏附速率(NFSL)。

其中,FSSL指循环水管道金属表层的年平均腐蚀厚度[6],表征循环冷却水对管道的腐蚀速率,其计算见式(1),单位为mm/a。

(1)

式中:G为试件腐蚀后减少的质量,g;A为试验管内表面面积,cm2;S为试样腐蚀面积,cm2;D为金属密度,g/cm3。

NFSL指循环水管道内部单位面积年平均沉积污垢的增长量[6],其计算见式(2),单位为mg/(cm2·a)。

(2)

式中:G1为试验管试验后的质量,mg;G2为试验管试验去除污垢后质量,mg;T为试验时间,d。

此外,按照机器学习方法建模的要求,对所有变量数据进行归一化处理[11],降低不同变量数据因数量级的差异而影响预测结果的准确性。归一化处理后的数据样本作为预测模型的输入数据,以保证机器学习算法的速度和精度。

1.2 特征变量选择

1.2.1最大互信息系数

经过数据预处理后,保留了14个水质指标变量。由于仍存在部分输入变量与目标变量间相关性很低、变量间独立性差、存在冗余变量等情况,因此,还需对保留的水质指标进行选择。特征变量选择是指从已知特征中选取隐含信息量较大的特征以减少数据集维度的方法,其能有效提高模型的效率。采用最大互信息系数衡量14个水质指标与预测目标变量间的相关性强弱,进而找到具有代表性的特征变量。将保留的14个水质指标的数据样本经过归一化后,以FSSL和NFSL为目标变量,分别计算其他12个水质指标与目标变量间的MIC值,结果见表1。

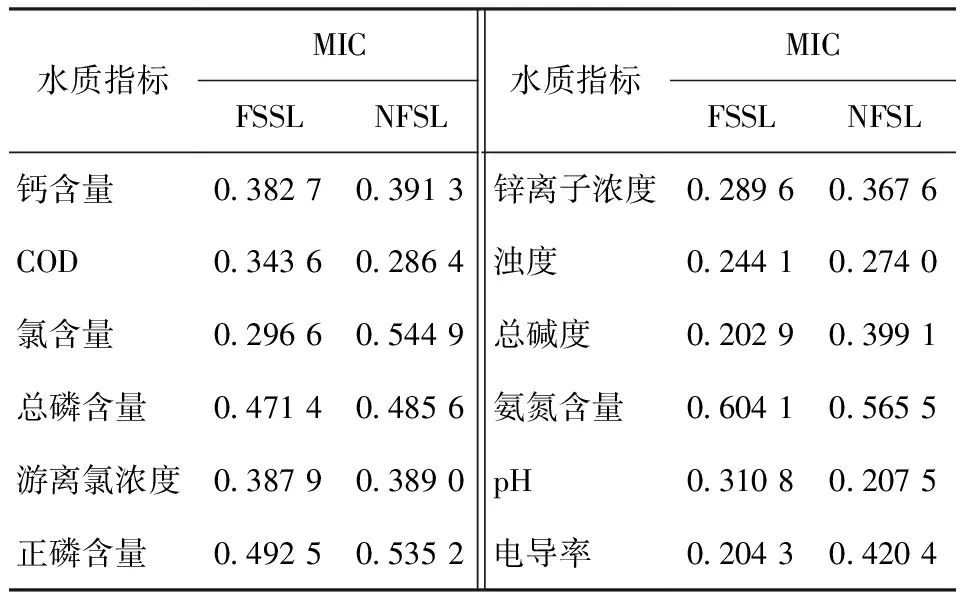
表1 各水质指标与FSSL和NFSL之间的MIC值

为了使模型具有说服力,应保留大部分有效变量;而为了提高模型模拟效率,需要精简建模变量。综合分析发现,当MIC在0.3以上时,相关指标之间具有较高的相关性[7]。因此,针对FSSL预测建模,需要精简掉MIC小于0.3的指标,但由于要保留更多的有效变量,将MIC值接近0.3的氯含量和锌离子浓度2个指标保留,去掉总碱度、电导率和浊度3个指标,最终留下钙含量、COD、氯含量、总磷含量、游离氯浓度、正磷含量、锌离子浓度、氨氮含量、pH总共9个指标。同理,针对NFSL预测建模,去掉COD、浊度和pH 3个指标,最后留下钙含量、氯含量、总磷含量、游离氯浓度、正磷含量、锌离子浓度、氨氮含量、总碱度和电导率总共9个指标。

1.2.2Pearson相关性分析

为了解决输入变量之间的多重共线性问题,筛选出独立性较强的建模变量,利用Python平台通过Pearson相关系数(r)法对上述保留输入变量间的相关性进行分析,结果见图1。研究表明,当r绝对值大于0.6时,变量间线性相关性显著,只保留其一即可[8]。由图1可知:对于目标变量FSSL预测模型,各输入变量间的r绝对值均小于0.6,故保留所有输入变量;而对于目标变量NFSL预测模型,r绝对值大于0.6的输入变量只有电导率,故将其剔除。

图1 FSSL与NFSL预测模型输入变量间的Pearson相关性分析

综合MIC和r的分析结果,最终确定针对目标变量FSSL预测模型的输入变量共9个,分别为钙含量、COD、氯含量、总磷含量、游离氯浓度、正磷含量、锌离子浓度、氨氮含量、pH;针对目标变量NFSL预测模型的输入变量共8个,分别为钙含量、氯含量、总磷含量、游离氯浓度、正磷含量、锌离子浓度、氨氮含量、总碱度。

2 预测模型的建立

分别采用BP神经网络、KNN回归和XGBoost 3种机器学习算法,建立的循环水系统以FSSL和NFSL为目标变量的预测模型。将预处理后的899组数据样本按照4∶1的比例随机划分成训练集和测试集,用于所建模型的训练和测试,用于模型评价的指标有均方误差(MSE)、拟合决定系数(R2)和MAPE。依据客户对循环水系统腐蚀和结垢程度的预警要求,其FSSL和NFSL的预警限值分别设定为0.7 mm/a和10.8 mg/(cm2·a)。899组数据样本中,FSSL和NFSL超出预警限值的数据样本分别有95组和39组。

2.1 BP神经网络模型

BP人工神经网络是最常用、最成熟的神经网络之一[12]。其包含输入层、隐含层和输出层,其中隐含层可以有多层。其计算主要分两个阶段:一是信号的前向传播;二是误差的反向传递[13]。通常具有单隐含层的网络可以映射出所有的连续函数,只有映射函数不连续时才会考虑设计多个隐含层[14]。

本研究采用3层结构BP神经网络建立循环水系统FSSL和NFSL的预测模型。激活函数采用ReLU函数[15]。建立神经网络模型的关键是确定隐含层神经元数,隐含层神经元数计算见式(3)。

(3)

式中:H为隐含层神经元数;m为输入层神经元数;n为输出层神经元数;L为1～10区间内的一个可调常数。

对于FSSL和NFSL预测模型,由式(3)得到隐藏层神经元数为4～13。因此,分别建立隐含层神经元数为4～13的BP神经网络预测模型,将数据导入模型中,在相同的初始权值和参数(激活函数为ReLU函数,迭代次数为1 000,损失函数为MSE,优化方法采用动量法,学习率设定为0.1)下进行训练,并比较每次计算结果的MSE和R2,结果见图2。从图2可知:对于FSSL模型,隐含层神经元数为8～12时对应的MSE最小,但其相差不大;而隐含层神经元数为10时,训练结果的R2最大。同理可知,NFSL预测模型的最佳隐含层神经元数为7。因此,基于BP神经网络方法建立的FSSL和NFSL预测模型的结构分别为9-10-1和8-7-1。

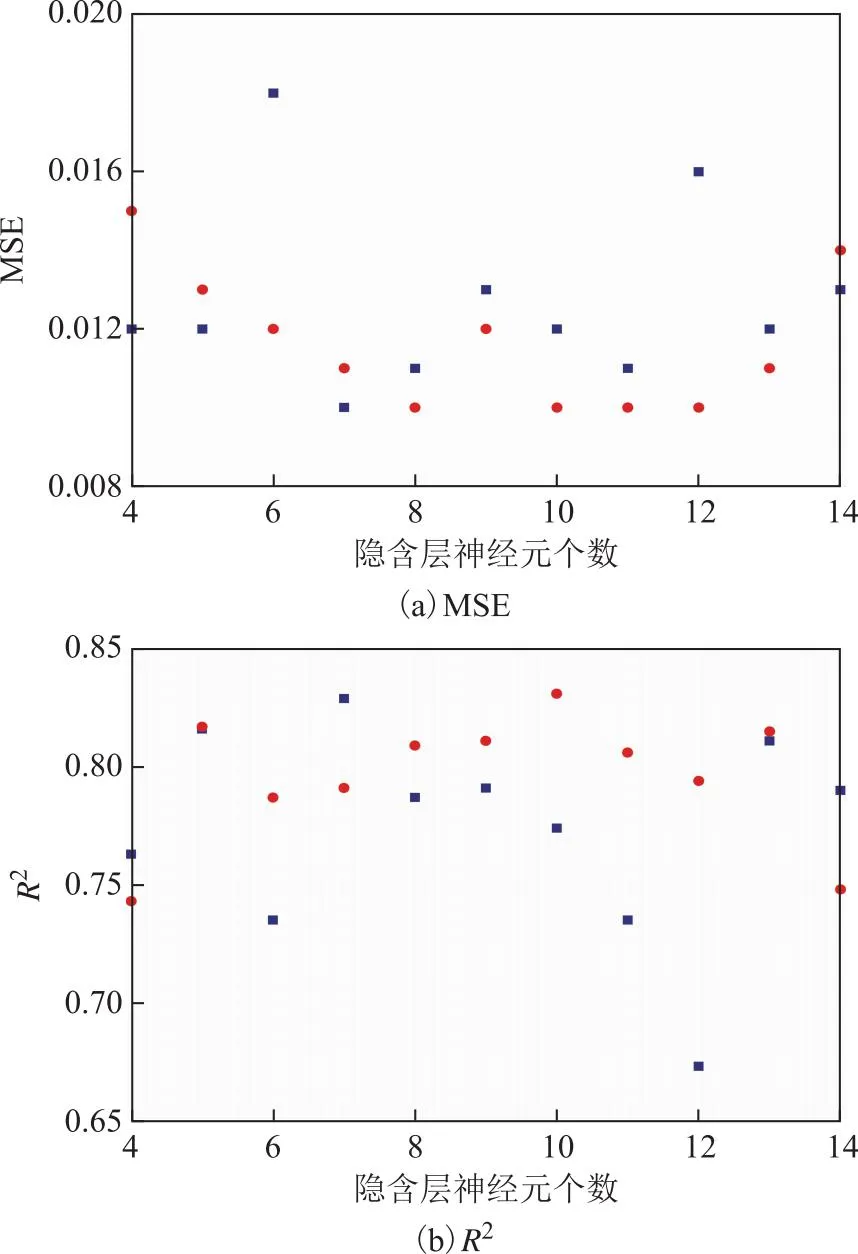
图2 隐含层神经元数与预测模型MSE和R2的关系

图3为基于BP神经网络的FSSL和NFSL预测模型在测试集数据的拟合结果,图中绿色线为预警限值。从图3可以看出,两预测模型预测值与实际值的拟合效果较好。

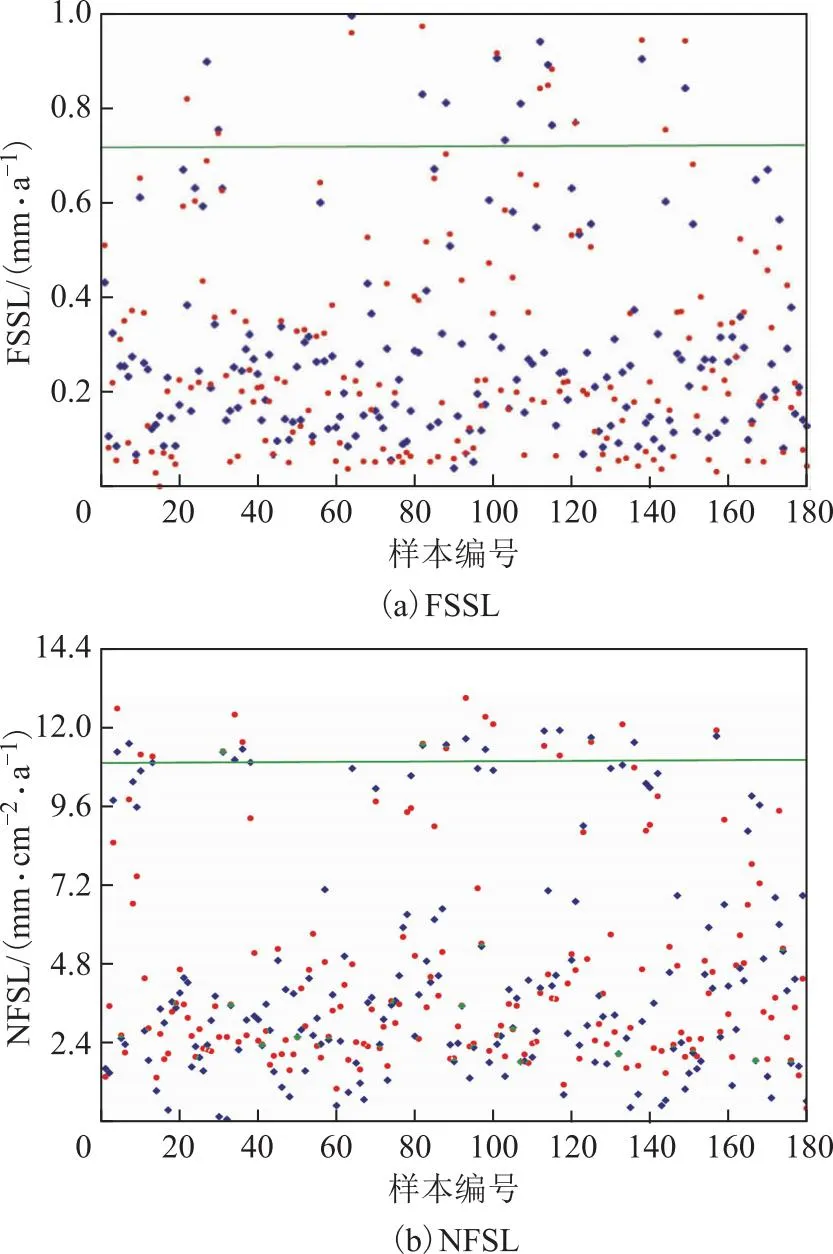
图3 BP神经网络模型对测试集的FSSL以及NFSL的预测结果

2.2 KNN回归模型

KNN回归算法[16]是一种有监督的学习算法,具有简单易实现、实时性好、计算效率高等优点。基于数值相似的KNN回归算法依据近邻状态欧式距离最小进行回归预测[17],其选取数值上最为近似的k个近邻样本,将这些样本的加权平均值当作预测结果。该算法主要包括以下3个步骤:

(1)最佳k值的选取

不同的k值对模型预测的准确性有较大的影响。若k值偏小,则可能会造成模型过拟合;反之,则可能造成模型欠拟合。为了选取最佳k值,在不同的k值下构建KNN水质预测模型,模型MSE最小时对应的k值即为最佳k值,结果见图4。

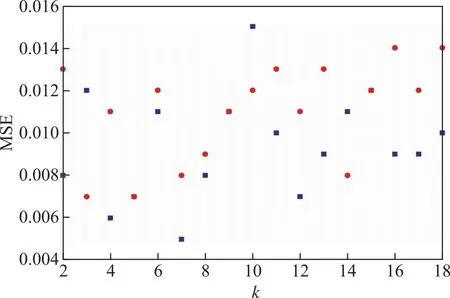
图4 FSSL和NFSL模型的MSE与k的变化关系

由图4可见:FSSL预测模型的最佳近邻样本数为7;NFSL预测模型的最佳近邻样本数为3或5,但比较发现,k=3时的模型R2=0.846,而k=5下的模型R2=0.812,前者拟合效果更好,故NFSL预测模型的最佳近邻数为3。

(2)相似性度量方法选取

在样本数据有限的情况下,k近邻样本的选取结果和距离度量方式有直接关系。一般来说,选择欧式距离作为相似性判定指标可以满足要求,见式(4)。

(4)

式中:Ui为数值相似预测方法的第i个样本的状态向量;uj(i)为Ui的第j个元素值;V为数值相似预测的待预测时间点的状态向量;vj为V的第j个元素值。

(3)预测值计算

基于KNN回归方法,利用最佳k值分别构建FSSL和NFSL的预测模型,模型对测试集数据样本的预测值与实际值对比结果见图5,图中绿色线为预警限值。从图5可见,两个预测模型预测值与实际值的拟合效果均较好。

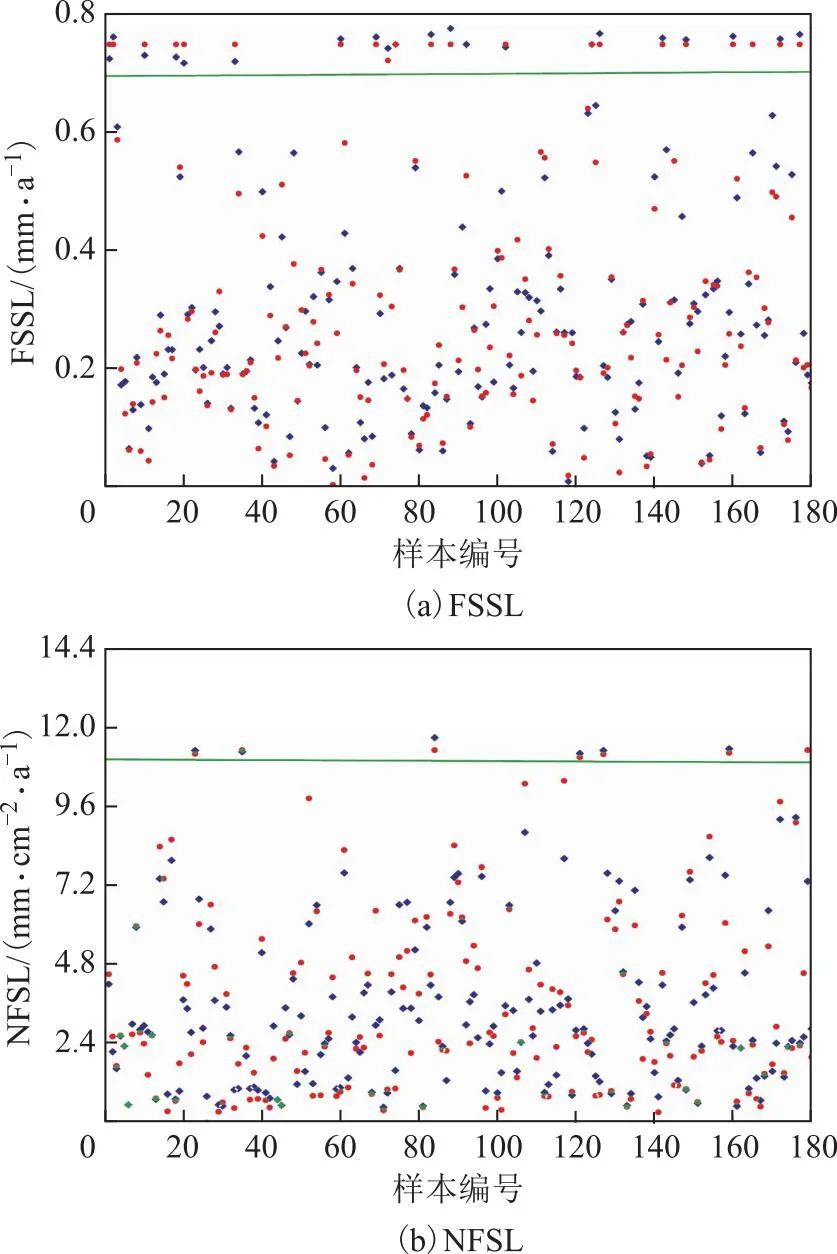
图5 KNN模型对测试集的FSSL与NFSL的预测结果

2.3 XGBoost模型

XGBoost是基于回归树的提升算法[18]。为了得到预测性能更佳的模型,需要对相关参数进行寻优和选择。

(1)损失函数的选择

XGBoost建模常用的损失函数L包括对数损失函数和平方损失函数两种[19]。对数损失函数用于分类任务,而平方损失函数用于回归任务。本文建立的模型为回归预测模型,故建模损失函数选择平方损失函数。

(2)回归树个数的选择

回归树个数(J)代表XGBoost模型的复杂程度,J过大,则模型会复杂化,易导致模型过拟合;J过小,则模型简单,易导致模型拟合不足。图6展示了针对目标变量FSSL构建的XGBoost模型的R2与J的变化关系。从图6可以看出:当J增加到80时,R2达到最大;当J继续增大时,R2不再增大。因此,XGBoost模型回归树数量优选80个。

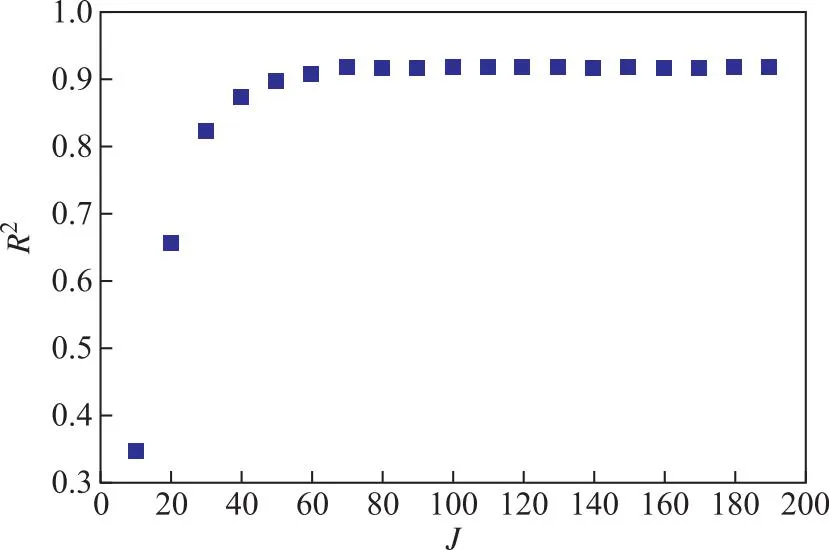
图6 R2随J的变化关系

(3)回归树的最大深度和子节点的最小分裂阈值的选择

回归树的最大深度(Ψ)用于调节单个回归树节点分裂的深度,Ψ值越大,模型越倾向于学习更局部的样本,越容易出现过拟合。子节点的最小分裂阈值(Ω)用来控制子节点分裂。若子节点的权重小于Ω,则其停止分裂。Ω较大时,可以防止模型仅限于学习局部特殊样本。

Ψ和Ω之间会相互影响,对其进行网格搜索法寻优,结果见图7。由图7可知,当Ψ为7、Ω为3时,针对目标变量FSSL模型的R2最大,故Ψ和Ω分别选择7和3。

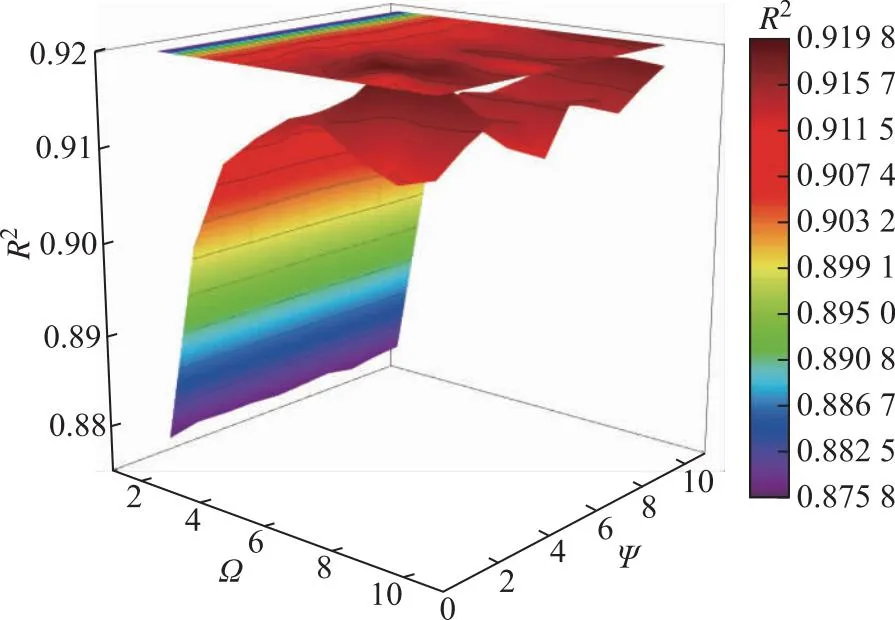
图7 R2随Ψ和Ω的变化关系

(4)正则化系数的选择

合理设定正则化项,可以避免模型过拟合。γ为回归树上的叶子节点数目的L1正则化系数,λ为叶子权重的L2正则化系数,对其采用网格搜索法寻优,结果见图8。由图8可知,当γ为0、λ为1时,针对目标变量FSSL模型的R2达到最大值,故γ和λ最优值分别为0和1。

图8 R2随γ和λ的变化关系

同理,对NFSL的XGBoost模型重要参数进行寻优,XGBoost模型主要参数寻优结果见表2。

按照表2寻优参数分别建立FSSL和NFSL的XGBoost预测模型,其对测试集数据样本的预测效果见图9,图中绿色线为预警限值。从图9可以看出,两个预测模型预测值与实际值的拟合效果较好。

图9 针对FSSL与NFSL的XGBoost模型对测试集数据样本的预测结果

2.4 模型预警性能的评价

综合3种模型的预测精准性的分析结果见表3。从表3可以看出,3种模型的预测值与实际值拟合效果较好,其MAPE均在9%以下,性能均优于文献[1-7,14]中的模型,其中基于XGBoost方法所建模型的MAPE最小,均在5%以下,R2最大,均在0.9以上,因而表现出最佳的拟合效果和泛化能力。

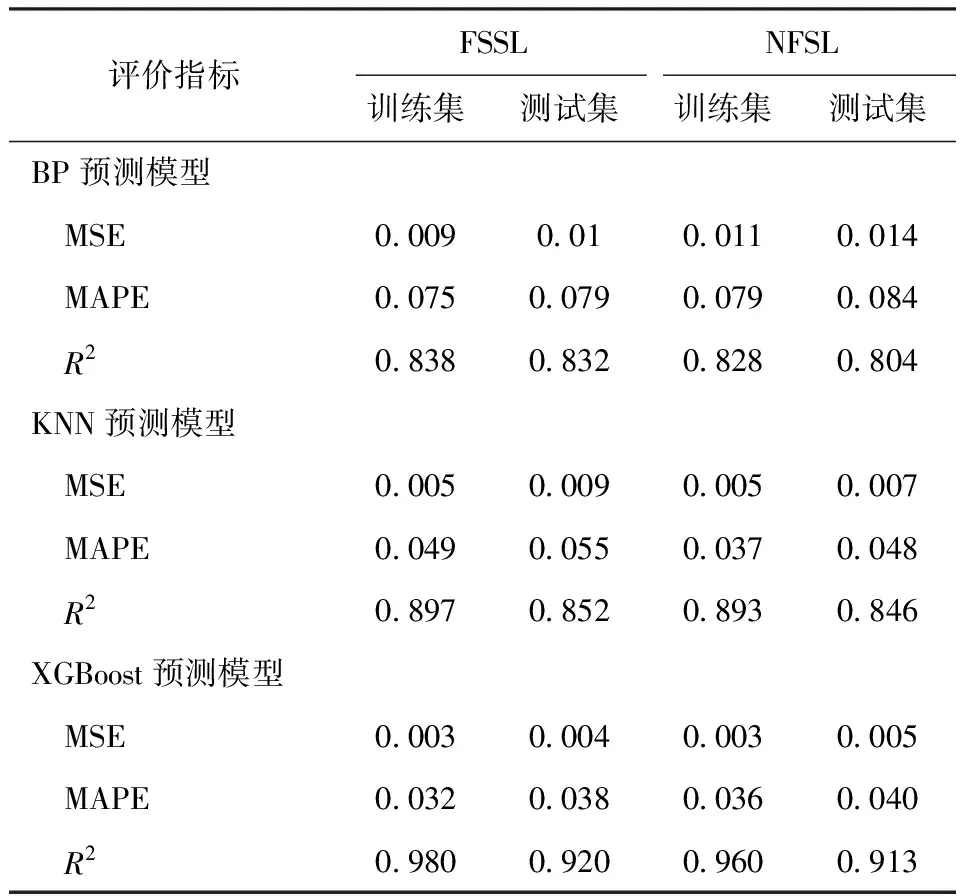
表3 3种模型预测精准性评价结果对比

将图3、图5和图9中3种FSSL和NFSL预测模型对测试集数据样本预测值超出预警值的个数(X)与样本实际值超过预警值的个数(Y)进行结合,可以计算出3种FSSL和NFSL预测模型各自的预警准确率(Z);进而,也分别计算了模型对训练集数据样本的预警效果(对应的X,Y,Z),详见表4和表5。从表4可以看出,XGBoost模型预警准确率最高,其对目标变量FSSL的训练集和测试集预警准确率均在90%以上,而对NFSL的预警准确率达100%。这表明,采用XGBoost方法建立的循环冷却水系统FSSL和NFSL预测模型,可以为该系统的腐蚀、结垢预警提供重要指导。

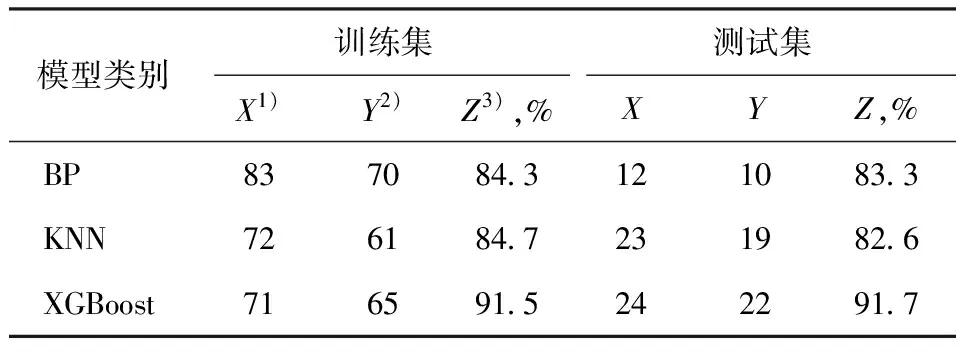
表4 3种预测模型对FSSL的预警效果

3 结 论

(1)基于LIMS系统采集的包含24个月水质化验指标的1 015组数据,运用箱线图等方法进行了数据预处理,得到保留14个水质指标的899组有效数据样本。

(2)采用最大互信息系数和Pearson相关系数法,从14个水质指标中进行特征变量选择,针对以FSSL和NFSL为目标变量预测模型,分别筛选出9个和8个输入变量,为模型的建立奠定了基础。

(3)分别采用BP神经网络、KNN回归和XGBoost机器学习算法建立了FSSL和NFSL预测模型,经验证,3种模型均具有较好的拟合效果和泛化能力,其对FSSL的预警准确率分别为83.3%,82.6%,91.7%,对NFSL的预警准确率分别为87.5%,85.7%,100%。3种模型中,基于XGBoost方法所建模型的性能最佳,可为石化企业循环冷却水系统的良好运行提供及时、有效的指导。