考虑输入和接种的时滞新型冠状病毒传播模型的最优控制策略

李雅芝,张香红,刘利利

(1.黔南民族师范学院 数学与统计学院,贵州 都匀 558000;2.西南大学 数学与统计学院,重庆 400715;3.山西大学 复杂系统研究所,太原 030006)

新型冠状病毒感染肺炎疫情在我国已流行3年有余,在“乙类甲管”的强有力控制下,我国经受住了全球疫情的多轮冲击。根据国务院应对新型冠状病毒感染疫情联防联控机制综合组制定的《关于对新型冠状病毒感染实施“乙类乙管”的总体方案》,2023年1月8日起,我国对新型冠状病毒感染疫情开始实施“乙类乙管”。对新型冠状病毒感染者不再实行隔离措施,不再判定密切接触者;不再划定高低风险区,检测策略调整为“愿检尽检”[1]。

使用数学模型研究传染病的传播特征及防控措施对实际工作有一定的指导作用,国内外对传染病流行规律和发展趋势的数学建模与定量研究已有多年历史。1927年Kermack等构造了著名的“易感者-感染者-恢复者(susceptible-infective-recovered,SIR)”模型,并在1932年提出了“易感者-感染者-易感者(susceptible-infective-susceptible,SIS)”模型,提出了疾病是否流行的“阈值理论”,为传染病模型研究奠定了基础[2]。近20年来,我国传染病动力学的研究进展极为迅速,大量的数学模型被用于分析各类传染病问题。在新型冠状病毒感染疫情暴发初期,陕西师范大学唐三一教授团队和西安交通大学肖燕妮教授团队做了非常多有意义的工作[3-6]。近期,张晶等[7]提出了一个改进的虫口模型描述新型冠状病毒的传播动力学过程,利用少量疫情相关数据对局部地区暴发的某一特定疫情进行了预测。于振华等[8]考虑了政府管控和个人防护等措施,在经典的SIR模型基础上引入了低风险群体,提出了一种新型冠状病毒传播动力学“易感者-低风险人群-感染者-恢复者(susceptible-low-risk-infective-recovered,SLIR)”模型,并验证了模型的有效性。任建强等[9]提出了一个基于机器学习的新型冠状病毒传播3步预测模型,将神经网络和随机森林等机器学习算法引入到新型冠状病毒的传播预测中。李淑萍等[10]建立了带有环境病毒的新型冠状病毒传播模型,分析了模型的动力行为,并将带有环境病毒、不带环境病毒的模型与我国早期新型冠状病毒感染数据进行了拟合。

现有文献主要集中于“乙类甲管”期间的研究,论文将研究建立符合防控政策的新型冠状病毒传播模型。全国整体疫情处于局部零星散发状态,但新型冠状病毒并未消失,病毒在人群中的传播仍持续存在,而且人口的流动也大幅增加,而最有效的防控措施仍是接种疫苗和个人防护。因此,将建立具有外部输入、疫苗接种、自我防护的新型冠状病毒传播模型,探讨其最优控制策略[11]。

1 模型建立

首先,将人群分为5个舱室,分别为:易感者S(t)、疫苗接种者V(t)、无症状感染者A(t)、有症状感染者I(t)和恢复者R(t)。记N(t)=S(t)+V(t)+A(t)+I(t)+R(t)。

其次,做如下模型假设:

1) 考虑无症状感染者和有症状感染者的外部输入;2) 考虑免疫消退和疫苗失效;3) 只考虑有症状感染者的因病死亡;4) 当前医疗资源已非常充足,感染后需要住院都可以得到满足,故不考虑住院舱室;5) 恢复者在短期内不会再被传染。

基于假设1)～5),为了研究自我防护和疫苗接种的力度随着时间的变化情况,分别加入控制u1(t)和u2(t)。由于易感者和接种者从感染新型冠状病毒到具有传播力是有一定滞后的,故可建立时滞微分方程模型(1),该模型的建立可为常态化防控传染病提供建模思路。

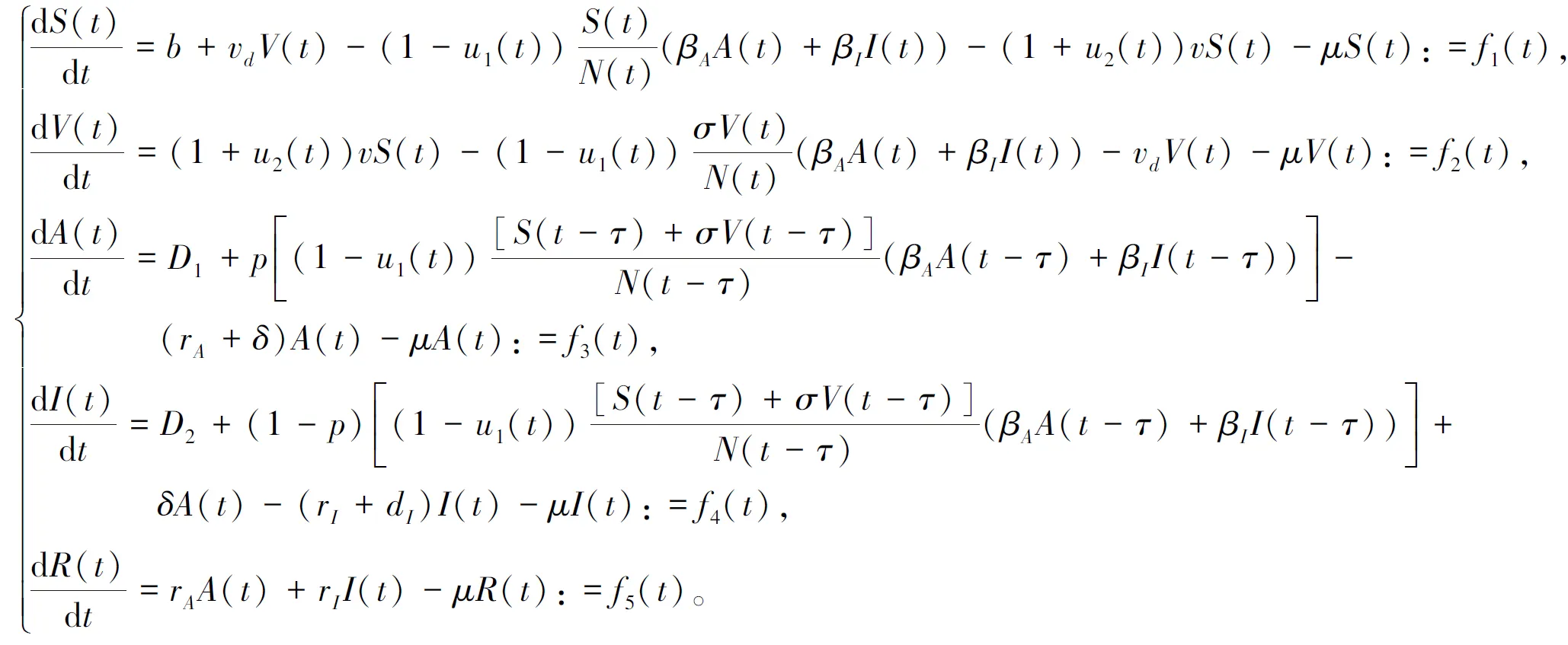
(1)

模型(1)中各参数的含义如表1所示。由表1可知所用的14个参数的含义。

表1 模型(1)参数含义Tab.1 Description of the parameters of model (1)

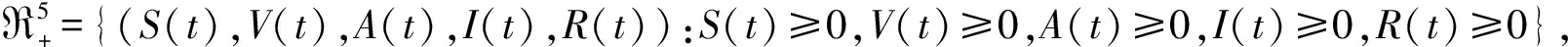
模型(1)的初始条件为

S(θ)=φ1(θ),V(t)=φ2(θ),A(t)=φ3(θ),I(t)=φ4(θ),R(t)=φ5(θ),

(2)

其中,φi(θ)∈C且φi(θ)≥0(i=1,2,3,4,5),θ∈[-τ,0]。

定理1在初始条件(2)下,模型(1)的解是非负且最终有界的。

定义函数G2(t)=A(t)+I(t)+R(t),由于βA和βI均小于1,则

dII(t)-μ(A(t)+I(t)+R(t))<

D1+D2+(1-u1)(S(t-τ)+σV(t-τ))-μ(A(t)+I(t)+R(t))≤

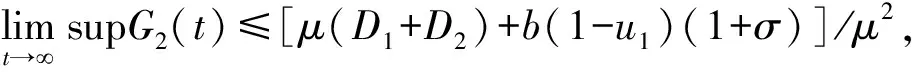
2 最优控制问题

主要探讨模型(1)的最优控制问题,实际控制总是希望在实施控制的时间段内以最少的成本使得感染者数量达到最少,故定义目标泛函为

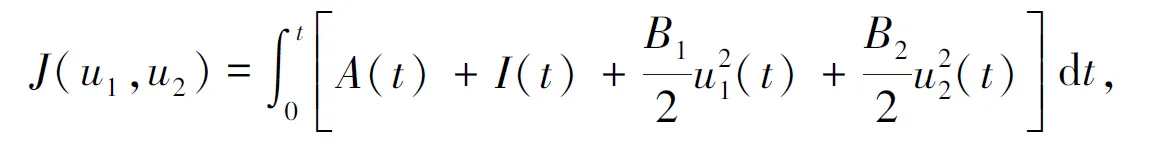
(3)

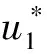
2.1 最优控制的存在性

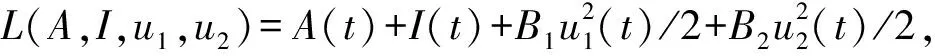
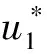
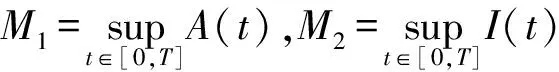
2.2 最优控制的特征

具体地,λi(t)(i=1,2,3,4,5)满足下面方程组:

(4)

横断条件为

λi(T)=0,i=1,2,3,4,5。

(5)

关于最优控制的特征,有如下结论:

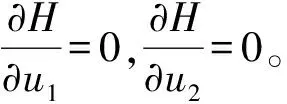
再结合控制约束集Λ的上下界,即可得到最优控制的特征表达。

3 数值模拟

主要通过数值模拟讨论以下3方面的内容:外部输入对模型动力学行为的影响,最优控制随时间的变化,以及控制对无症状和有症状感染者感染规模的影响。数值模拟的参数选取为b=300,μ=2.06×10-5,v=0.3,vd=0.1,σ=0.3,βA=0.4,βI=0.5,rA=0.3,rI=0.3,rA=0.3,rI=0.3,δ=0.1,dI=0.01,p=0.5。时滞选取为τ=7。初值选取为:S(θ)=1000,S(θ)=1000,V(θ)=50,A(θ)=5,I(θ)=5,R(θ)=0,θ∈[-τ,0]。

3.1 输入率的影响

当控制不存在时,通过数值模拟探讨外部输入对易感者、接种者、无症状和有症状感染者规模的影响,结果如图1所示。

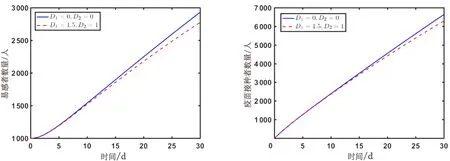
(a) 易感者数量时间序列 (b) 疫苗接种者数量时间序列

由图1可知,当无症状感染者A(t)和有症状感染者I(t)存在外部输入时,1个月内各类人群规模的变化。由图1(a)和图1(b)可知,由于A(t)和I(t)数量的增加,导致更多的易感染者S(t)被感染,因此易感者数量有所下降,相应使得接种者数量下降。对比图1(c)和图1(d)可以看出:在第30d时,若无外部输入,A(t)的量约为40,I(t)的量约为80;但当存在外部输入时,A(t)的量约为100,I(t)的量约为220,是无外部输入情形下数量的两倍多。因此,外部输入会扩大传染病在当地的蔓延,需要引起足够重视。

3.2 最优控制变量的时间序列

当控制存在时,输入率选取为D1=1.5,D2=1,且在实际中,控制很难做到100%,故控制最大值选取为0.8。

4组不同控制成本下最优控制随时间变化的结果如图2所示。由图2(a)可知,自我防护控制成本远大于疫苗接种控制成本,自我防护在高成本情形下在最大值持续时间短,为了达到更好的防控效果,疫苗接种由于其成本低可以维持在较高水平。由图2(b)可知,自我防护控制成本远小于疫苗接种控制成本,自我防护在低成本情形下可以在最大值持续较长时间,而为了节约成本,疫苗接种始终处于低水平。由图2(c)可知,自我防护和疫苗接种控制成本一样且取值较小,此时,自我防护在最大值持续时间较长,而疫苗接种力度保持中等水平。由图2(d)可知,自我防护和疫苗接种控制成本一样且取值较大,此时,自我防护在最大值持续时间很短便开始下降,而疫苗接种始终维持在较低水平。

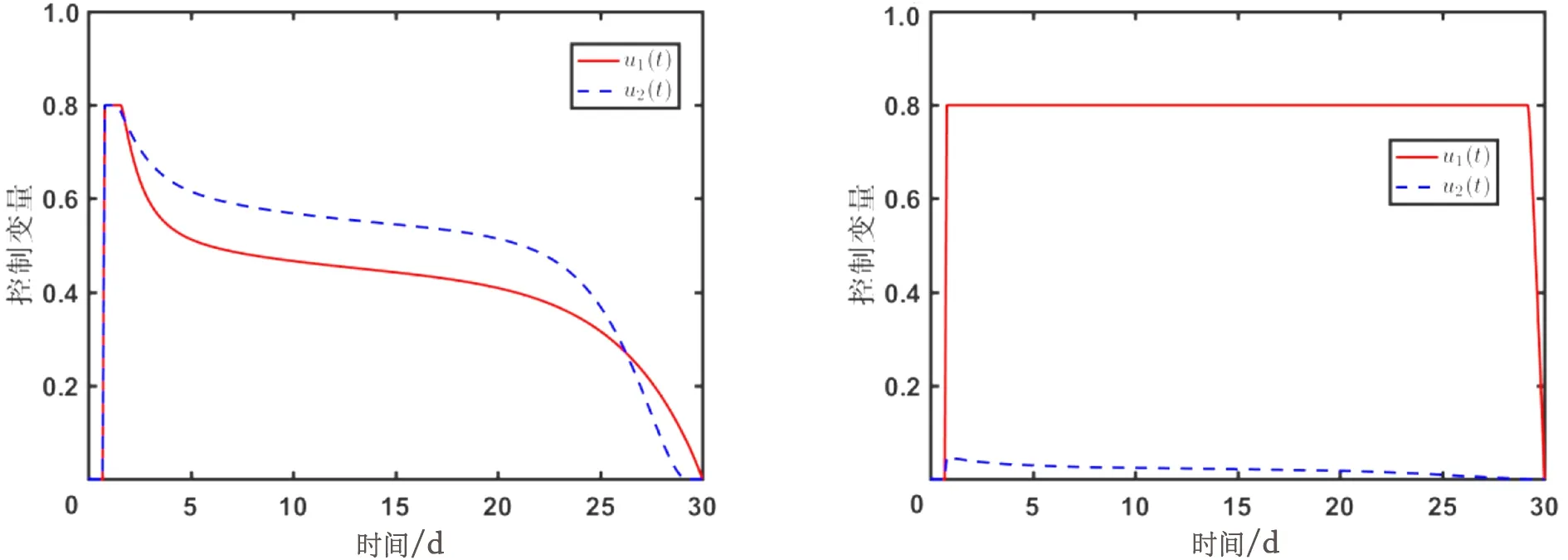
(a) B1=12,B2=1时控制变量时间序列 (b) B1=1,B2=12时控制变量时间序列

对比图2(a)和图2(b)可知,自我防护控制成本无论是低还是高,其控制力度都较大,说明自我防护对于预防新型冠状病毒传染起着无可替代的作用,即使成本高,也应积极采取自我防护措施;而疫苗接种成本一旦升高,只要自我防护做得好,本着节约成本的原则,可以采取低水平疫苗接种控制。对比图2(c)和图2(d)可知,当2种控制措施成本同时升高时,自我防护不能长时间维持在高水平,疫苗接种控制也只能维持在低水平。对比图2(a)和图2(c)可知,当疫苗接种成本较低且保持不变时,若自我防护成本降低,可以通过加大自我防护控制,适当降低疫苗接种力度;反之,若自我防护成本升高,其控制力度会减弱,但可以通过增大疫苗接种力度达到最佳控制效果的目的。对比图2(b)和图2(d)可知,当疫苗接种成本较高且保持不变时,虽然可以通过加大疫苗接种力度弥补自我防护力度的减弱,但疫苗接种力度始终维持在较低水平。

3.3 不同控制力度的影响

为了探讨不同控制策略对无症状感染者A(t)和有症状感染者I(t)感染规模的影响,分别给出3组常数控制及其最优控制下A(t)和I(t)的数量变化,输入率选取为D1=1.5,D2=1,目标函数中权重选取为B1=12,B2=1,结果如图3所示。

由图3可知不同控制组合下无症状感染者和有症状感染者的数量变化。对比图3(a)和图3(b)可知,对于常数控制,随着控制变量的增大,A(t)和I(t)的数量均在下降,并且在最优控制情况下,A(t)和I(t)的数量达到最少。对比图3(c)和图3(d)可知,自我防护的单一控制效果优于疫苗接种的单一控制效果。

4 建议和结论

基于以上发现,为了做好疫情常态化防控,相关部门应特别注意在旅游旺季或某些大型活动等人流量较大的情形下,做好外部输入引发疫情的风险评判以及应急管理等。当前人们对采取防护措施已经有所松懈,社区或媒体仍应做好自我防护的宣传和教育,以提高大家的自我防护意识。此外,疫苗接种仍是疫情防控的有效措施,但在无条件接种疫苗的情况下,做好自我防护是最有效的防控措施。最后,在实际工作中,应追求最优综合控制措施,以达到最佳控制效果。

研究了基于外部输入的实际情况,考虑了自我防护和疫苗接种,建立了1个五维时滞微分方程模型刻画新型冠状病毒在人群中的传播,以花费最少的成本达到感染者最少为目标,探讨了最优控制策略。基于极值原理得到了最优控制的特征表达,并通过数值模拟讨论了外部输入对疫情的影响,不同控制成本组合对最优控制变量的影响,以及不同控制组合的控制效果。发现:1) 外部输入使得感染者数量出现大幅增加,进而导致更多的易感者被感染;2) 无论控制成本如何,自我防护的控制力度始终维持在较高水平,但疫苗接种力度会因为控制成本的升高而大幅下降;3) 对于常数控制的不同组合,控制力度越大,感染者数量越少,且最优控制效果最佳;自我防护单一控制力度优于疫苗接种单一控制力度。

研究结果对实践具有一定的参考价值,可对未来应对处于常态化防控且具有类似特征的传染病提供防控经验,然而还有一些方面需要改进。首先,当新发传染病暴发时,决策者很难及时识别其传染性和危害性,因此,实施有效防控措施具有一定的滞后。其次,死亡病例主要集中在患有某些潜在疾病的老年人身上,因此,感染具有一定的年龄结构。另外,疾病往往在某个区域暴发,然后向四周蔓延,因此,空间分布也是疾病传播的一个因素。基于以上因素,建立更符合实际的数学模型,得到更丰富的研究结果,是未来努力的方向。