基于风险权重的综合传动装置任务可靠性预计
黄大荣,张传普,高 剑,魏盛兴,孙雪岩,桂 林,李 攀
(1.重庆交通大学 信息科学与工程学院,重庆 400074;2.重庆交通大学 数学与统计学院,重庆 400074;3.中国北方车辆研究所 车辆传动重点实验室,北京 100072;4.北京航空航天大学 可靠性与系统工程学院,北京 100191)
某履带车辆综合传动装置是集机电液为一体的复杂装置,包含前传动、液压操纵系统等20个部件近万个零件。综合传动装置为整车提供直驶变速、转向、制动、压气机驱动、风扇驱动等功能,是车辆正常完成任务的基础装置。为了适应现代复杂多变的工作内容和实际情况中未知的各类环境,保证车辆的持续工作能力和任务成功性就显得尤为重要。对综合传动装置在给定工作或非工作条件下的可靠性参数进行估算,能够得到系统的可靠性指标。该指标是一种将设备可靠性由定性转为定量评估的有效方法[1-3],预测结果可用于评估维修预算和改进设计[4-5]。然而,现有对综合传动装置可靠性方面的研究大多针对装置内特定类型的元件或部件,很少有针对综合传动装置整体可靠性的研究。可靠性预计作为定量分析综合传动装置可靠性的有效手段,所得的精确可靠的预计结果对于综合传动装置系统设计、改进和维护具有重要意义。
可靠性框图是一种常见的可靠性预计方法,其用框图形式描述产品(系统)可靠性与零部件故障之间的逻辑关系[6]。Zhou等[7]、斗计华等[8]、吴嘉宁等[9]、孙晓哲等[10]分别构建相应的可靠性框图,有效解决了风电变流器电容器组、舰空导弹武器系统、飞机主控制系统等可靠性分析问题。Bhardwaj等[11]、郑凤翥等[12]从系统的失效机理出发,通过故障模式、影响和危害性分析(failure mode and effects criticality analysis,FMECA)方法分别有效提高了风力涡轮机系统、伺服稳定平台的可靠性。赵健等[13]采用系统工程方法解决了装备基本可靠性指标的分配问题。综合传动装置是由大量机械件、电气件以及液压液力器件等不同类别的零件组成,部件结构复杂且种类差距较大,在系统中地位和功能各不相同,采用传统可靠性框图法进行可靠性预计存在定量计算精度不足、预计方法缺乏针对性和适应性的问题。产品设计阶段往往面临故障数据不足等问题,缺少对真实故障数据的研究,会导致可靠性预计结果参考意义较小。因此构建系统可靠性模型时需综合考虑各单元对系统可靠性的影响权重,并区别处理[14],有利于提高可靠性预计结果的准确性。
针对综合传动装置元件种类多、数量大以及执行任务复杂等特点,以某履带车辆综合传动装置为研究对象,提出一种基于风险权重的综合传动装置任务可靠性预计方法。在设计部件-系统关联架构下的任务可靠性预计流程的基础上,基于部件任务风险权重系数构建部件层次任务可靠性预计修正模型,实现各类型目标任务模式下整体装置可靠性的准确预计。
1 部件-系统关联架构下任务可靠性预计
在实际工程中,综合传动装置是由不同单元部件组成的复杂系统,各部件的可靠性与其任务目标相关,一般通过部件分层逐级迭代进行可靠性预计分析。为提高综合传动装置可靠性预计的准确度和合理性,需将层次分析法与可靠性框图相结合,建立不同单元、不同层次的可靠性预计模型,采用分层次、分类别的流程进行可靠性预计,划分为元件、部件和系统3个层次,部件层次的可靠性预计结果可作为系统层次可靠性预计的输入。整体系统的可靠性预计流程和指标要求如图1所示。

图1 综合传动装置可靠性预计流程Fig.1 Integrated transmission reliability prediction process
由图1可知,部件层和系统层的可靠度将直接影响系统整体可靠性预计结果的准确性。在实际应用中,不同部件层次在不同任务条件下的可靠性结果不一致,需要以FMECA表为基础,结合各部件权重因子大小,根据任务目标设定部件-系统层次可靠性计算模型。
2 部件层次任务可靠性预计修正模型
2.1 部件层次基本可靠性预计模型
综合传动装置内的部件由众多元件组成,元件可靠度的大小会影响部件可靠度。而部件层次可靠性框图是从可靠性角度出发研究元件与部件之间的逻辑图,基本可靠性框图内任一单元发生故障都需要进行维护。基于此,以中间支架部件为例,建立如图2所示的中间支架基本可靠性框图。
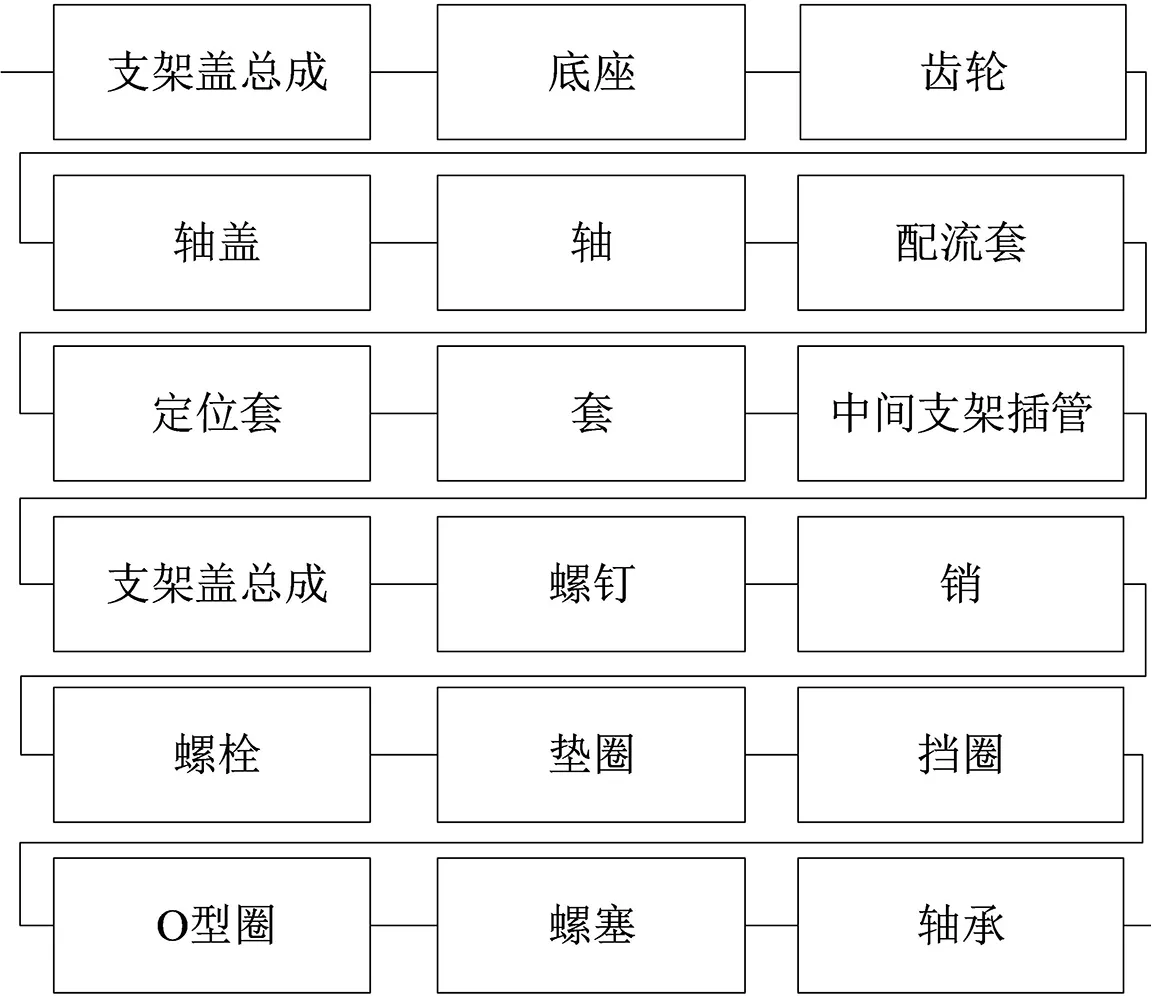
图2 中间支架基本可靠性框图Fig.2 Basic reliability block diagram of intermediate support
由图2可知,基本可靠性框图下组成部件的各元器件均有固定可靠度,用符号Rj表示。部件基本可靠度计算公式如下:
(1)
(2)
(3)
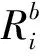
基于上述计算模型,可确定系统内部件的基本可靠度。在实际工程中,部件层次可靠度与任务目标可靠度相关,在实际操作中为了更准确地评估部件层次可靠性,需对部件层次的任务可靠性进行预计。
2.2 部件任务可靠性预计修正模型
部件层次任务可靠性与综合传动装置的任务要求和执行功能密切相关。各部件在不同任务目标下对整体系统可靠性综合评估结果的影响不一样,即与各部件对应的任务存在一定的可靠度偏离风险,称之为风险权重系数,记为W。显然,在获得部件的基础可靠度Rb后,还应根据各部件对整体系统的风险权重系数,对部件层次可靠度进行修正,称为部件层次任务可靠度,其基本计算公式可设定如下:
RB=(Rb)W。
(4)
式(4)中,RB为部件的任务可靠度;Rb为部件的基本可靠度。
实际应用中,风险权重系数的计算准确与否,将直接影响部件层次任务可靠度预计的准确性。因此,如何对部件风险权重系数进行准确估算,在实际操作中显得尤为重要。
2.3 风险权重系数计算方法的构建
在给定目标任务模式下,综合传动装置的各部件风险大小跟故障模式发生概率等级(occurrence probability rating,OPR)和影响严酷度等级(event severity rating,ESR)密切相关。在实际工程中,为确保风险权重系数影响下的部件层次可靠性预计结果符合实际需求,需要在对故障概率发生等级以及目标任务严酷度等级进行定义的基础上,建立合理的风险权重系数计算模型。
2.3.1 故障概率发生等级 综合传动装置的故障模式发生概率等级评分准则如表1所示。由表1可知,故障模式的发生概率等级通常是根据历史数据或者经验来估计的。

表1 故障模式发生概率等级Tab.1 Probability level of failure mode
2.3.2 严酷度等级 严酷度是对零部件故障造成的最坏潜在后果的度量。根据故障对综合传动装置任务功能的影响程度,综合传动装置严酷度类别定义及评分准则如表2所示。由表2可知,中间支架由支架盖总成、底座等18类元件构成,任何一类元件出现故障,都会导致该部件发生故障。

表2 综合传动装置严酷度类别定义及评分准则Tab.2 Classification definition and grading criteria for harshness of integrated transmission devices
2.3.3 基于模糊矩阵的风险权重系数计算模型 基于上述定义,即可引入合理的算法设计相应的风险权重计算模型。基本思想是:在对综合传动装置进行FMECA表分析的基础上,结合故障模式发生的概率等级和影响严酷度等级,构建指标重要性的二元对比矩阵,并引入模糊矩阵,实现部件风险权重系数的计算。基本步骤如下:
1) 计算风险优先系数。基于实际应用目标的FMECA分析表,获取各元件的部件故障模式发生的概率等级和部件层次对系统层次的影响严酷度等级评估结果,并计算任务目标下部件的风险优先数,计算公式为
NRPNi=∑NOPRi·NESRi。
(5)
式(5)中,NRPNi为部件i的风险优先数;NOPRi为部件i故障模式发生的概率等级;NESRi为部件i对系统的影响严酷度。
从而,得到各部件的风险优先系数矩阵为
NRPN=NRPN1,NRPN2,…,NRPNB。
(6)
式(6)中,i=1,2,…,B;B为总元件数。
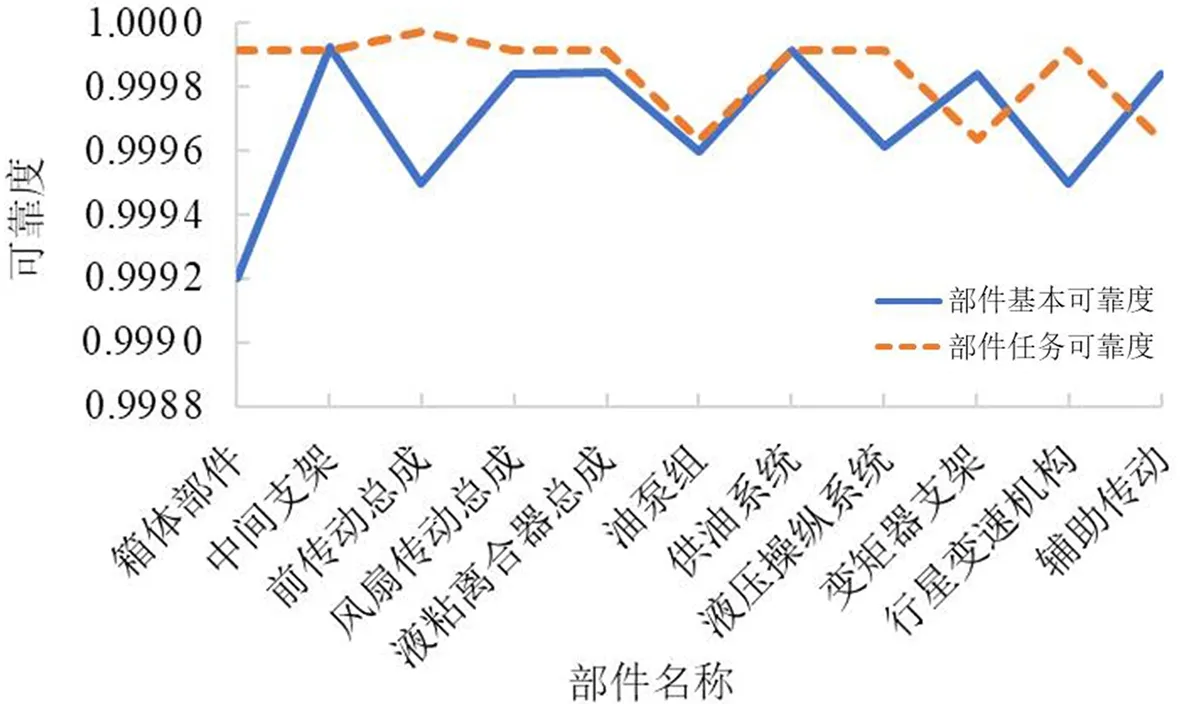
2) 建立关于指标重要性的二元对比矩阵。对风险优先系数矩阵NRPN中的NRPNi与NRPNj作二元对比,j=1,2,…,B。当NRPNi>NRPNj时,排序标度eij=1、eji=0;当NRPNi=NRPNj时,排序标度eij=0、eji=0;当NRPNi 根据排序标度建立关于指标重要性的二元对比矩阵E: (7) 3) 计算某部件的风险优先系数。根据二元对比矩阵结果,计算NRPNi的重要性排序指数fi,定义如下: (8) 根据fi的大小,即可得到部件可靠度相对于系统的重要度排序结果。 为进一步对比分析两两部件间的相对重要度,引入模糊隶属度概念进行计算,具体模型如下: wij=(fi-fj)/[2(B-1)]+0.5。 (9) 对综合传动装置整体而言,可得到两两部件间的相对重要模糊隶属度矩阵,称之为模糊判断矩阵M,即: (10) 最终,通过指标排序指数变换,得到描述指标相对重要度的模糊间接标度,并通过模糊判断矩阵数值wij得到每行模糊隶属度结果。即: (11) 式(11)中,wi为部件i相对于上层次(也就是系统层次)的重要性,即部件i的风险优先系数。 4) 计算部件i的风险权重。将得到的风险优先系数先进行算术平均,再利用各个部件的权重值除以总权重的平均值,得到各个部件的风险权重系数。风险权重系数计算公式为 (12) 式(12)中,Wi为部件i的风险权重系数;A为系统下部件的总数量。 通过上述算法,就可以根据各个部件的基本可靠度和对应权重得到部件任务可靠度的修正结果,从而确保最终可靠性预计结果的准确性。 综合传动装置在完成任务时,每个部件都会参与,且每个部件都有各自的功能,因此各部件在系统中都是相互独立的,在逻辑上又是相互关联的。因此,一旦确定了部件层次任务可靠度结果,就需要针对综合传动装置整体系统的组成架构,构建系统层次可靠性框图,如图3所示。 图3 系统层次基本可靠性框图Fig.3 System level basic reliability block diagram 由图3可知,采用上述修正算法得到综合传动装置的任务可靠度计算公式: (13) 式(13)中,R为综合传动装置系统任务可靠度;RB为综合传动装置部件任务可靠度。 为验证所提出算法的有效性和合理性,采用某履带车辆的综合传动装置进行验证,其中测试速度默认值为20km/h,工作测试时间默认值为1h。同时,为保证车辆完成任务,规定平均故障间隔里程大于5000km。 可靠性预计过程采用自底向上的原则。首先,在对该装置进行可靠性框图分析的基础上,根据部件层次基本可靠性框图,结合元件层次的基本可靠度和式(1),求得综合传动装置部件-系统层次基本可靠度如表3所示。由表3可知,综合传动装置中,中间支架、供油系统等部件基本可靠度较高,箱体部件、前传动总成、行量变速机构等部件基本可靠度较低。 表3 部件-系统层次基本可靠度Tab.3 Basic reliability of component-system level 为修正任务模式下的可靠性预计结果,根据式(5)~(12),利用Matlab软件进行计算,得到的任务模式下各部件风险权重系数如表4所示。由表4可知,风险权重系数是在考虑任务风险的概率、影响程度等因素下对综合传动装置的分析和评估,可对部件基本可靠度进行加权得到部件任务可靠度。 表4 部件层次风险权重系数Tab.4 Basic reliability of component level 根据目标任务模式下部件权重系数,结合部件基本可靠度和式(4),得到的部件层次任务可靠度如表5所示。 表5 综合传动装置部件任务可靠度修正结果Tab.5 The improved results of task reliability of integrated transmission components 由表5可知,在工程设计阶段,将各部件任务可靠度代入到式(13)中,计算得到综合传动装置系统任务可靠度为0.9977932,平均故障里程为9053.06km,大于规定的平均故障间隔里程指标。 综合传动装置的各部件基本可靠度和部件任务可靠度对比结果如图4所示。由图4可知,在完成任务过程中,油泵组、变矩器支架和辅助传动任务可靠度较低,相比于其他部件,更影响整个综合传动装置的任务完成能力。另外,从综合传动装置各类任务执行参与程度和FMECA表中可以得出液粘离合器总成、行星变速机构、前传动总成和油泵组为行驶中重要参与部件。因此,液粘离合器总成、行星变速机构、前传动总成和油泵组可认为是综合传动装置的重要部件。在实际设计中,为提升综合传动装置的可靠性和稳定性,建议该装置的可靠性设计和改进需重点关注液粘离合器总成、行星变速机构、前传动总成、油泵组、变矩器支架和辅助传动。 图4 部件基本可靠度与部件任务可靠度结果对比Fig.4 Comparison of component basic reliability and component task reliability 同时,在整个传动系统任务可靠性预计方面,综合传动装置具有较高的任务可靠度,超过了预计规定的5000km平均故障间隔里程,能有效保证其任务成功。实验结果表明,综合传动装置的任务可靠性预计值是规定值的1.81倍,兼顾性能设计的同时还能为传动系统后续优化设计提供更大的改进空间,可以通过加强各个部件中元件的筛选、选用更高质量等级的元件、简化设计、降额设计和热设计等措施进一步提高装置的基本可靠性和任务可靠性水平。 综合传动装置作为履带车辆中的关键子系统,其可靠性预计结果直接影响整车的质量,其部件-系统层次可靠性预计方法,是工业管理部门特别关注的问题。特别地,受限于综合传动装置中不同类别零部件的功能和风险差异性,在给定任务模式下,其可靠性预计精度不高。基于上述目的,在传统可靠性预计流程的基础上,设计了目标任务下部件风险权重系数计算模型,并以此为基础提出了一种基于风险权重的综合传动装置可靠性预计新方法。根据上述方法计算综合传动装置整体的任务可靠度为0.9977932,平均故障里程为9053.06km,大于定量规定的平均故障间隔里程。实验结果表明,提出的算法具备一定的合理性和有效性,可对工业设计部门提供一定的改进建议。3 系统层次任务可靠性预计方法

4 实验案例分析
4.1 实验结果
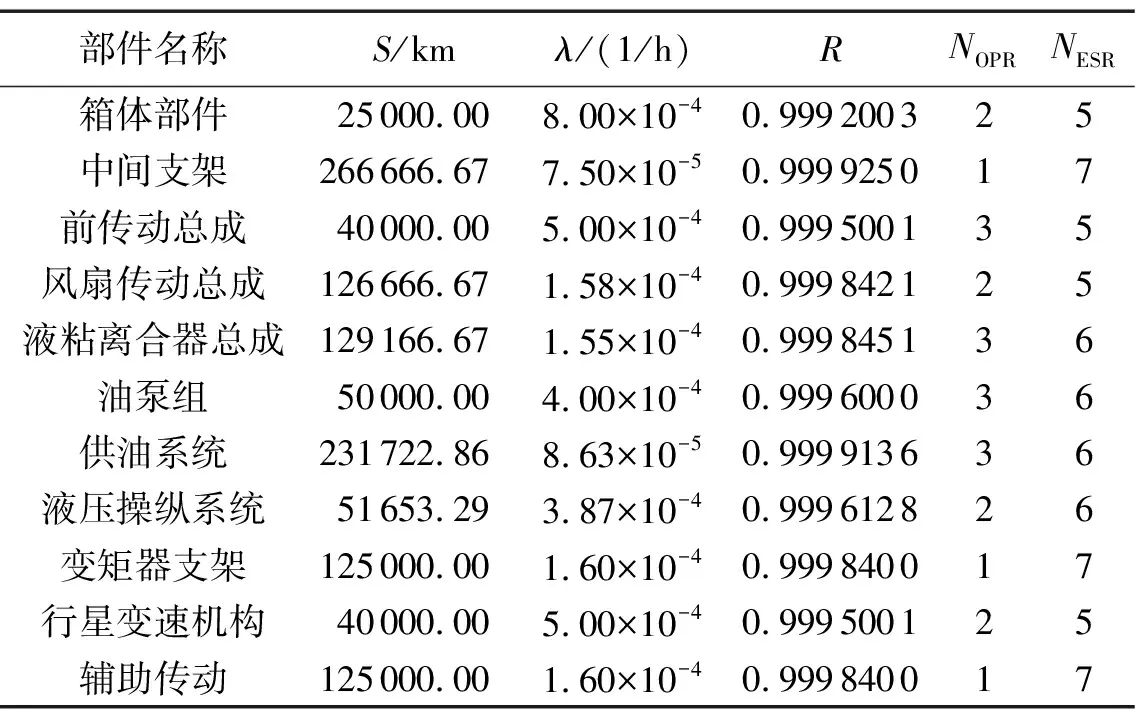
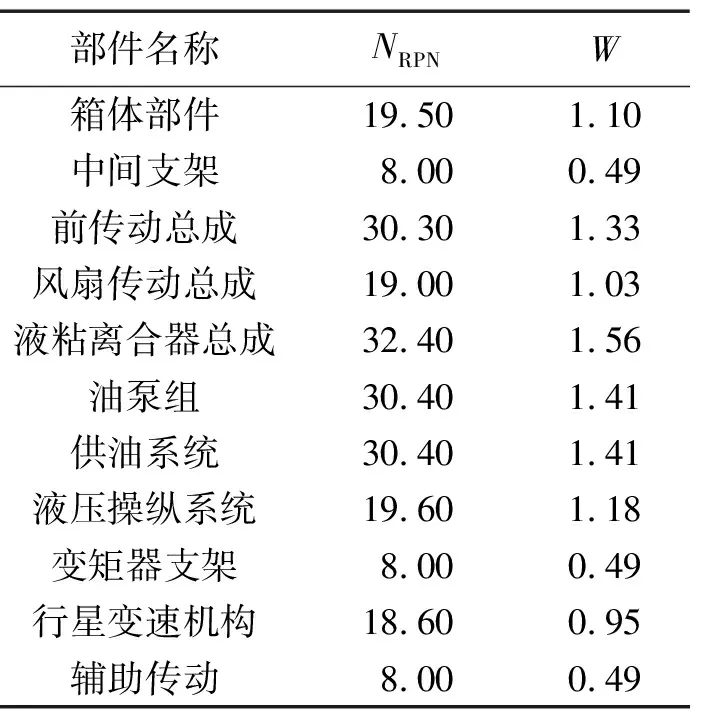

4.2 实验结果分析
5 结论

