NGO-VMD和SSNGO-RF算法在风机齿轮箱故障诊断中的应用

陈 萱,杨永超*,袁博洋,郭光华,2,钟建伟

(1.湖北民族大学 智能科学与工程学院,湖北 恩施 445000;2.湖北能源集团新能源发展有限公司,武汉 430073)

近年来,随着风电场的建设,大量风电机组投入运行,相关故障问题也不断出现。风力发电机常位于高山和海洋等风能资源丰富却巡检不便的地区,出现的故障无法及时发现。其中,齿轮箱作为风机传动系统的关键部件,一旦出现故障,将会对风机的正常运行造成严重威胁,甚至可能导致严重的安全事故和重大经济损失。因此,对风机齿轮箱进行状态监测与故障诊断成为了重要课题[1]。由于齿轮箱工作环境复杂、背景噪声强烈,为了尽可能多地提取到有效信息,降低风机齿轮箱振动信号的噪声干扰,美国学者Dragomiretskiy于2014年提出了新的自适应信号变分模态分解(variational mode decomposition,VMD)模型。VMD模型是完全非递归的信号分解算法,在计算过程中摒弃了递归分解的约束条件,有效避免了模态混叠问题和白噪声残留问题,提高了信号分解速度,对非平稳、非线性信号具有良好的处理效果,因此被广泛应用于降噪、故障诊断和识别分类领域[2-3]。VMD模型对分解层数(K)与惩罚因子(α)依赖较强,K较小会导致振动信号欠分解,产生模态混叠问题,K较大则会导致振动信号过分解,产生模态丢失问题[4];α过大会导致分解得到的本征模态分量带宽减小,造成信息缺失,α过小会导致分解得到的本征模态分量带宽增加,出现中心频率重叠和模态混淆[5]。为了对VMD模型中的参数K与α进行寻优,郑小霞等[6]提出了灰狼优化算法-VMD与极限学习机相结合的齿轮箱故障类型识别算法,使用灰狼优化算法寻找最优的K并进行模态分解,使故障识别准确率得到了有效提高。张萍等[7]提出鲸鱼优化算法(whale optimization algorithm,WOA)对VMD模型参数K与α寻优,但该算法易出现陷入局部最优的问题。为了更加准确地提取振动信号特征,各种更高性能的优化算法被广泛应用于VMD模型参数K与α的优化。如2021年Dehghani等提出北方苍鹰优化算法(northern goshawk optimization,NGO),将其与粒子群算法(particle swarm optimization,PSO)等8种著名算法对比发现,NGO算法在迭代次数和速度上具有更好性能,比同类算法更具竞争力[8]。Cao等[9]提出了采用NGO算法对K进行寻优的方法,其检测效果较未对K进行寻优的VMD算法有一定提高。付雪等[10]提出了改进混沌映射NGO算法,并与经典的、当前主流的群智能优化算法进行对比分析,证明了改进后的算法具有更好性能。但NGO算法容易因种群初始化过程中初始种群分布不均的原因产生局部极值问题,进而会对算法的优化效果产生不利影响。

为了对特征向量进行分类,从而实现对风机齿轮箱的故障诊断,采用机器学习是当前使用较多的方法。其中,2001年由Leo提出的随机森林(random forest,RF)算法具有性能优异、参数少、训练效率高且不易过拟合的优势[11],近年来被广泛应用到包括风机齿轮箱等设备故障诊断领域。宋来建等[12]将故障特征输入RF分类器进行故障识别,取得了很好的故障识别结果。秦喜文等[13]提出了基于VMD和RF的故障识别方法,并与支持向量机(support vector machine,SVM)等方法进行对比,验证了所提方法具有更高的诊断精度。RF算法对模型中子树棵数与分类特征数有较高要求,人工设定的方式难以对参数值进行选取,如果RF参数选取不当,会增加算法随机化概率,进而降低诊断准确率[14]。为了使RF算法性能最优,蒋文强等[15]提出基于粒子群优化随机森林的故障诊断方法,该方法通过粒子群优化算法寻找随机森林中子树棵数,克服了随机森林算法依靠人工设置关键参数的不足,并验证了该方法的有效性,但粒子群优化算法存在局部收敛精度低的问题[16]。叶丽珠等[17]采用经过WOA算法优化得到的随机森林模型进行非平衡数据分类,获得了更优的分类性能。王静等[18]运用哈里斯鹰算法(Harris hawks optimizer,HHO)确定RF参数,结果表明优化后的RF算法具有更高的分类准确率。但以上方法在优化算法中常存在种群初始化分布不均、易出现局部最优的问题,导致优化算法对RF参数寻优不准确,进而影响RF算法分类识别的准确性。

综上所述,为针对NGO算法存在问题进行改进,以求使初始种群均匀分布,并尽可能避免NGO算法陷入局部极值,保证诊断的准确性,提出基于NGO和VMD的NGO-VMD算法与结合一维复合混沌映射(sine map and piece wise linear chaotic map,SPM)、正余弦优化算法(sine cosine algorithm,SCA)的改进NGO算法(SSNGO)和RF优化算法(SSNGO-RF),对振动信号进行状态识别。首先,利用NGO算法优化VMD算法参数并分解原始振动信号,然后采用皮尔逊系数求解VMD算法分解得到的本征模态分量(intrinsic mode function,IMF)与原始振动信号的相关系数,再设定相关系数阈值,对阈值以上的重构分量提取特征向量,达到去噪和特征提取的目的,最后将特征向量输入SSNGO-RF模型中实现故障诊断。

1 基本原理

1.1 NGO-VMD算法

变分模态分解是将原始输入信号分解为若干个IMF的自适应分解方法,为确定IMF的带宽,VMD算法建立了如下约束变分问题模型:

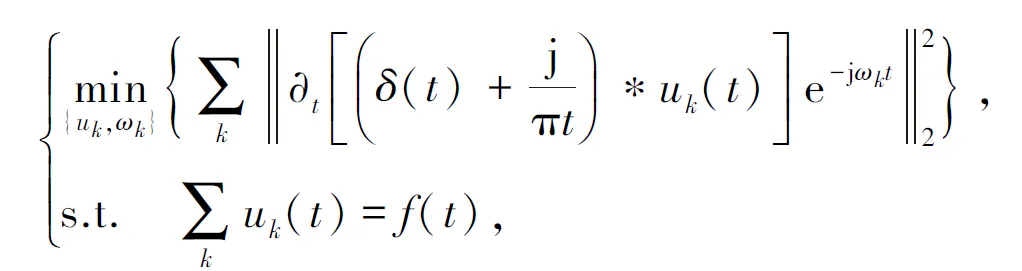
(1)

其中,k为分解的IMF个数;δ(t)为狄拉克函数;t为时间,单位为s;f(t)为原始输入信号;j为复数的虚部;*表示卷积运算过程;∂t表示梯度运算过程;{uk}为经VMD算法分解后k个IMF的合集;{ωk}为k个IMF的中心频率合集;uk(t)为各IMF的时域信号。

为求解式(1),Dragomiretskiy等[19]将式(1)由约束变分问题转变为无约束变分问题,引入拉格朗日算子λ和惩罚因子α,之后利用交替乘子方向算法(alternate direction method of multipliers,ADMM)对该变分问题的鞍点进行搜寻,以实现各IMF带宽和中心频率的更新。经ADMM算法求得k个IMF分量如式(2)所示:

(2)

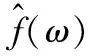
(3)

由上述VMD分解公式可知,VMD算法在分解信号过程中对分解层数K与惩罚因子α依赖性较强,如果分解参数选择不当易导致分解后的振动信号模态混叠或模态丢失,因此提出使用NGO算法对VMD算法参数进行优化。

NGO算法模拟了北方苍鹰的狩猎捕食过程,在完成算法初始化后,狩猎过程将分为2个阶段:1) 对猎物识别、选择攻击阶段,为了确定猎物的行动范围,在该阶段,北方苍鹰会进行全局搜索,对目标最优区域进行识别;2) 对猎物发起追击、完成捕获阶段,在该阶段,受到攻击的猎物会因本能进行逃亡,而北方苍鹰具有反应机敏的优势,将在半径R的范围内快速实现对猎物的最终捕猎[9]。

在猎物识别过程中,北方苍鹰对猎物进行随机选择并进行攻击。由于猎物选择是随机的,这一过程也体现了NGO算法在空间内的全局搜索能力,该过程的表达式如下所示:

Pi=Xk;i=1,2,…,N,k=1,2,…,i-1,i+1,…,N。

(4)

其中,Pi为第i只苍鹰选择的猎物位置,Xk为第k个初始化位置,k为区间[1,N]中的随机自然数。

(5)

(6)

在第一阶段北方苍鹰对猎物进行识别攻击后,第二阶段中,猎物会试图逃跑,而北方苍鹰的速度很快,可以通过追击最终实现对猎物的捕获。NGO算法对这一过程的模拟体现了局部搜索能力,该过程表达式如下所示:

(7)

其中,R为北方苍鹰进行追击的半径范围。

R=0.02(1-t/T),

(8)

其中,t为当前迭代次数,T为最大迭代次数。

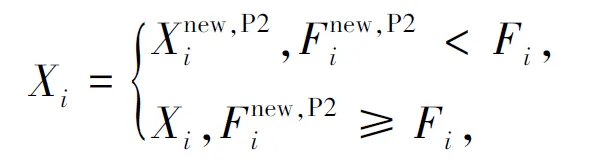
(9)

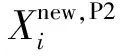
1.2 SSNGO-RF算法

在种群初始化阶段,NGO算法会生成随机数对初始种群进行部署,种群易出现分布不均的问题,导致错过潜在的最优解。在NGO算法优化过程中,北方苍鹰追逐猎物的速度极快,即算法的搜索速度很快,会导致在后期优化过程中算法易出现陷入局部极值的问题[10],对算法的迭代速度和迭代精度产生影响。为了尽可能避免NGO算法陷入局部最优,需要针对存在的不足进行改进,因此常采用混沌映射的方法对种群进行初始化,使初始种群分布更加均匀。选用Huang等[20]提出的SPM生成混沌序列方式对种群进行初始化。SPM混沌映射是结合正弦映射(sine map)与分段线性混沌映射(piece-wise linear chaotic map,PWLCM)的一维复合混沌映射,具有混沌映射遍历性的特性,可以遍历各种状态,同时也可解决正弦映射结构简单和PWLCM映射在零点,即x=0.5时,失去混沌性质的问题,从而使混沌范围扩大,产生更多的随机值。因此,将SPM混沌映射的遍历性引入NGO算法中,使初始种群分布均匀,可极大避免NGO算法陷入局部极值。

另一方面, SCA是利用正弦函数和余弦函数随机波动的范围大小进行优化的算法。为使正弦函数和余弦函数的波动范围可以在算法迭代中进行调整,以进一步提高NGO算法对最优解的搜索能力,并最大程度避免算法早熟收敛的问题,将NGO算法的猎物识别阶段与由李爱莲等[21]提出的改进SCA进行融合,进一步平衡算法的全局搜索与局部开发能力。实验中,SCA正弦因子与经由李爱莲等[21]改进后的惯性因子大小与迭代次数的增加呈负相关。在迭代初期,正弦因子与改进后的惯性因子数值较大,使算法具有更强的全局搜索能力;在迭代后期,随迭代次数增加而减小的正弦因子与改进后的惯性因子会使算法的局部搜索能力得到提升。将该算法与猎物识别选择阶段NGO算法进行融合,替代NGO中原有的北方苍鹰在第b维的位置更新计算方法,可以提高算法搜索能力,尽可能避免算法出现局部最优;最终形成结合SPM和SCA的改进NGO算法(SSNGO算法)。

此外,RF是集成算法,将多棵决策树作为基分类器进行集合构造而成。将输入数据随机生成M个数据集,作为训练子集并随机分配给M棵决策树训练,并将M棵决策树集合成1个综合模型,利用决策树集合的投票机制,将M棵决策树的判断作为投票结果,采取少数服从多数的理论实现分类功能[22-23]。在RF算法应用中,子树棵树和分类特征数作为关键参数对算法的结果影响很大[14]。子树棵树较多会增加RF算法的复杂度,导致计算时间增加,子树棵树过少又会增大分类误差;分类特征数较多会导致各决策树之间差异性降低,对分类结果产生影响,分类特征数较少会导致决策树过随机化,使分类准确性降低。因此,采用SSNGO算法对子树棵树和分类特征数进行选取,可使RF算法分类准确性得到提高。

1.3 故障诊断流程

使用NGO-VMD算法对原始振动信号去噪并提取特征向量,之后利用SSNGO-RF算法对特征向量进行故障诊断,诊断流程如图1所示。由图1可知,具体步骤如下:

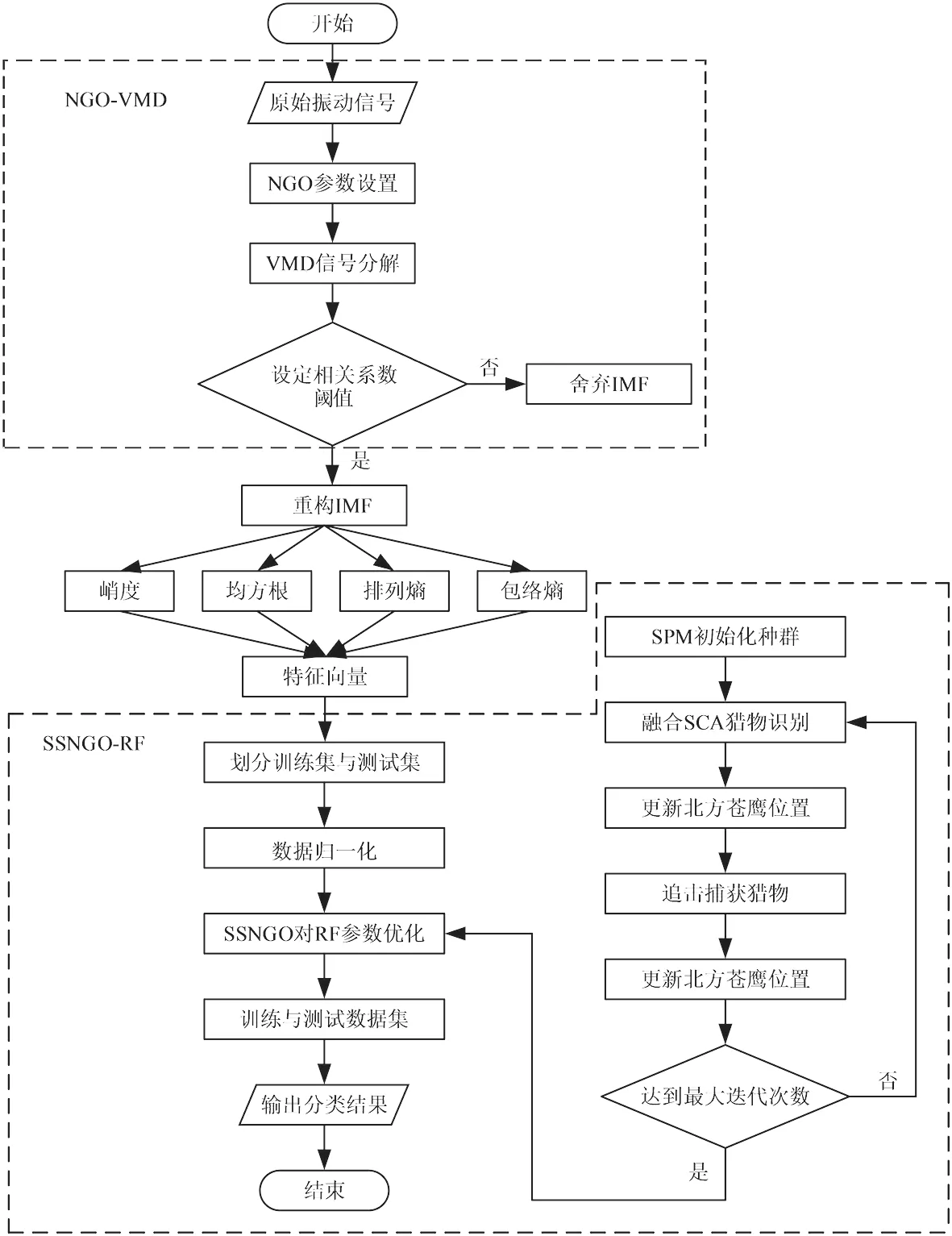
图1 NGO-VMD和SSNGO-RF算法诊断流程Fig.1 Flow chart of NGO-VMD and SSNGO-RF diagnosis

步骤1 利用NGO算法对VMD算法需要的2个参数分解层数K与惩罚因子α进行优化,选取最优解,实现VMD算法分解过程;

步骤2 求解VMD算法分解后的IMF分量与原始信号的相关系数,对相关系数的阈值进行设定,舍弃与原始信号不具有相关性的IMF分量,对具有相关性的IMF分量进行重构,实现原始振动信号的去噪;

步骤3 提取峭度、均方根、排列熵、包络熵作为重构信号的特征值,并将每组特征值组成多维特征向量;

步骤4 采用SSNGO算法对RF算法进行参数优化;

步骤5 将每种工况下提取的特征向量以7∶3的比例划分为训练集与测试集,并实现对不同运行状态的识别分类。

2 实验与结果

2.1 SSNGO算法性能测试

为了对SSNGO算法的收敛效果及鲁棒性进行测试,采用10种常用的智能优化算法测试函数对SSNGO和NGO算法的收敛速度和收敛精度进行对比。测试过程中,2种算法初始种群数量设为30,迭代次数设为500次。选用的10种测试函数如表1所示。

表1 选用的10种测试函数Tab.1 Selected 10 test functions

由表1可知,10种测试函数包括单峰测试函数、多峰测试函数、固定维测试函数3种类型,在每种类型中选取1种测试函数对NGO和SSNGO算法的迭代效果进行测试,测试函数图像与迭代曲线如图2所示。

(a) F2迭代曲线 (b) F9迭代曲线 (c) F10迭代曲线图2 测试函数F2、F9和F10的迭代曲线Fig.2 Iterative plot of test functions F2,F9,and F10

由图2可知,SSNGO算法的迭代曲线始终位于NGO算法下方,即SSNGO算法的收敛速度快于NGO算法,且收敛精度高于NGO算法。对2种算法在10种测试函数中的最优值、平均值和标准差进行统计,结果如表2所示。由表2可知,在迭代期间,SSNGO算法比NGO算法更接近测试函数的最优值,证明了前者比后者的迭代精度更为精准,并且在大多数情况下前者的平均值与标准差更小,进一步证明了SSNGO算法在迭代精度上的提高。

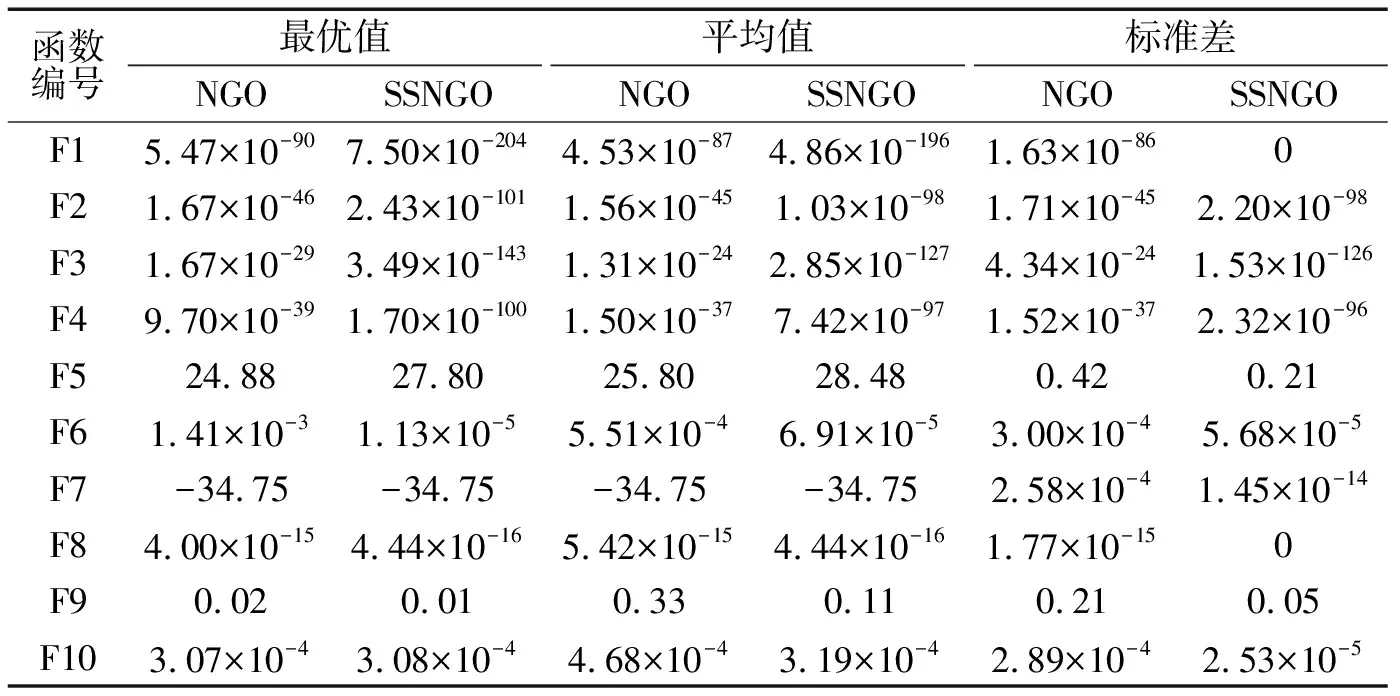
表2 测试函数结果统计Tab.2 Statistics of test function results

2.2 特征提取结果

为了对NGO-VMD算法和SSNGO-RF算法的故障诊断方法进行有效验证,实验测试过程设计如下:采用QPZZ-Ⅱ旋转机械振动分析及故障诊断实验平台系统对风机齿轮箱运行过程中的多种状态进行模拟[24]。设置采样频率为5120Hz,对该实验平台在转速为880r/min、加载电流为0.20A时的正常、断齿、点蚀、磨损4种风机齿轮箱常见运行状态的振动数据进行采集。在运行状态下分别采集51200个振动信号,并以每512个数据点分为一组,有100组,得到4种运行状态共计400组数据。

实验以880r/min的转速、加载0.20A电流时的一组正常运行状态和断齿状态的振动数据作为NGO-VMD算法分解示例,该组原始振动数据的时域波形如图3所示,频谱如图4所示。

(a) 正常 (b) 断齿图3 原始振动信号的时域波形Fig.3 Time domain waveform of the original vibration signal

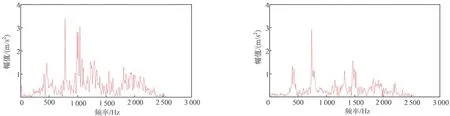
(a) 正常 (b) 断齿图4 原始振动信号的频谱Fig.4 Original vibration signal spectrum

由图3、图4可知,相较于正常状态下振动信号的时域图和频谱图,断齿状态振动信号对应的时域图和频谱图有明显的信号冲击;但仅从振动信号波形变化中很难直接对齿轮存在的具体故障类型进行准确判断。由于在优化效果相近的情况下,SSNGO-VMD算法分解时间是NGO-VMD算法的近10倍,因此,考虑到分解效率问题,采用NGO-VMD算法提取特征向量并通过SSNGO-RF算法进行状态识别分类,以对故障进行诊断;同时采用传统中心频率法确定VMD分解层数,与SSNGO-RF算法进行状态识别,对NGO-VMD算法与SSNGO-RF算法相结合的识别准确性进行验证。基于图4(a)中的振动数据,采用中心频率法确定VMD分解层数K及NGO-VMD算法过程示例,当计算出IMF中心频率相近的情况时,即可认为VMD算法过分解,出现了模态混叠现象[25]。中心频率与分解层数关系如表3所示。

表3 振动信号中心频率与分解层数的关系Tab.3 The relationship between the center frequency of vibration signals and the number of decomposition layers

由表3可知,在分解第8层(K=8)时出现了2个比较相近的中心频率1304.69Hz与1485.52Hz,因此判断存在过分解情况;在分解第7层(K=7)时,中心频率与第6层(K=6)相比变化不大;因此,根据中心频率法可知, VMD算法的分解层数K为7。

在NGO-VMD算法中,首先使用NGO算法对VMD算法进行参数优化,采用多次求解平均值的方式,确定VMD算法的最佳分解层数与惩罚因子。通过计算10次NGO参数优化的平均值确定VMD分解层数K为12,惩罚因子α为1412,使用这2个参数分解1组原始振动信号的IMF,结果如图5所示。由图5可知,通过使用NGO算法对VMD算法参数进行优化的方法,在分解后的IMF中未出现模态混叠和模态丢失的问题。

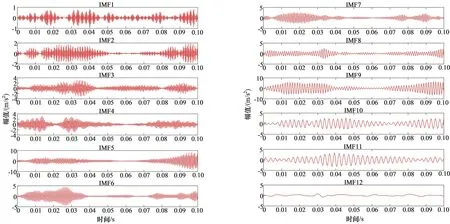
(a) IMF1～IMF6时域 (b) IMF7～IMF12时域

为了实现对原始振动信号的去噪,准确提取特征值,对12层IMF与原始振动信号的相关系数进行计算,12层IMF分量的相关系数如图6所示。

图6 各层IMF与原始振动信号的相关系数

由图6可知,分解信号第4、7、8层的相关系数大于0.30,即与原始振动信号存在相关性;因此,将相关系数大于0.30的IMF分量重构,可以达到保留原始振动信号中有用信息的目的。重构后的振动信号如图7所示。由图7可知,与图3(a)的原始振动信号时域波形相比,图7中的信号毛刺有所减少,有效体现了NGO-VMD算法的去噪效果。

2.3 分类及诊断结果

对经NGO-VMD算法分解并根据相关系数重构的每组振动信号提取包括峭度、均方根、排列熵、包络熵在内的4种信号特征值,并组成特征向量,可提高后续SSNGO-RF算法的故障诊断率。对880r/min转速、加载0.20A电流时不同状态的特征值进行分类,对应标签如下:正常状态为1,断齿状态为2,点蚀状态为3,磨损状态为4,每种运行状态取100组数据,共计400组。为验证SSNGO-RF算法的故障诊断准确率,将其与3种算法RF、PSO-RF、NGO-RF进行对比,把每组特征向量分别输入以上4种分类方法中;同时,为验证NGO-VMD算法的准确性,将传统的中心频率法确定的VMD算法与经NGO算法优化的VMD算法获得的不同去噪信号进行重构,并提取特征值,输入SSNGO-RF算法中进行状态识别,诊断结果如图8所示,图中检测结果以实际测试集分类(蓝色)为准,可通过比较实际测试集分类与预测测试集分类(红色)竖向的重合情况来表征。

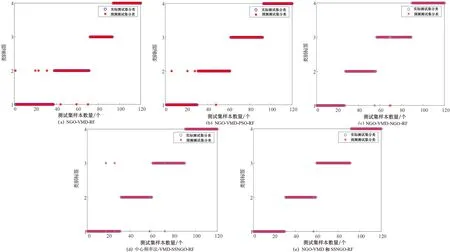
图8 不同分类算法的诊断结果Fig.8 Graph of diagnostic results of different classification algorithms

由图8可知,在未经任何优化算法对RF算法进行参数优化时,样本中存在较多的错误分类,其中,正常运行状态和断齿状态中分别有4个和3个测试集样本分类错误(见图8(a));采用PSO算法对RF算法进行参数优化后,错误分类数量减小,在正常状态和断齿状态中分别有3个和1个测试集样本分类错误(见图8(b));采用NGO算法对RF算法进行参数优化后,错误分类数量会进一步缩小,在断齿状态和点蚀状态中分别有1个和2个测试集样本分类错误(见图8(c));采用中心频率法优化VMD算法时,SSNGO-RF算法在正常状态中有2个测试集样本分类错误,在断齿状态和点蚀状态中各有1个测试集样本分类错误(见图8(d));而在采用NGO-VMD算法时,SSNGO-RF算法的诊断准确率得到有效提高,仅在断齿状态下有1个测试集样本分类错误(见图8(e))。各分类算法的准确率及运行时长如表4所示。

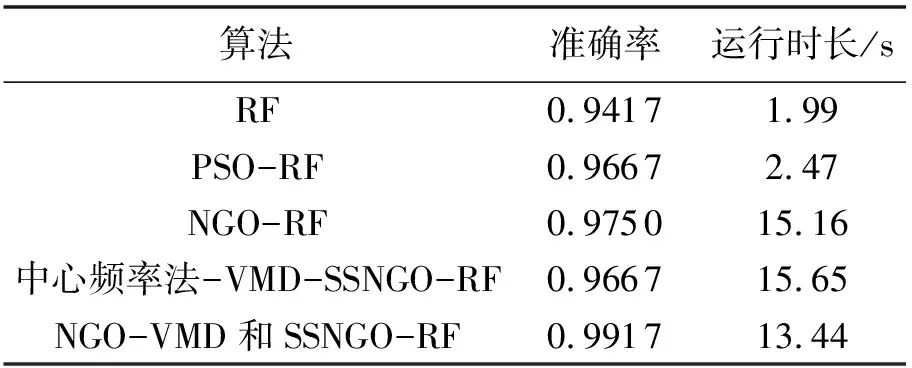
表4 各分类算法准确率对比Tab.4 Accuracy comparison of classification algorithms

由表4可知,在使用NGO-VMD算法去噪时,SSNGO-RF算法的准确率可达0.9917,比RF算法准确率高了0.0500,比PSO-RF算法高了0.0250,比NGO-RF算法高了0.0167。在运行时长方面,由于RF和PSO-RF算法较简单,虽然运行时长较短,但准确率较低。NGO-RF与NGO-VMD和SSNGO-RF算法虽然运行时间长,但准确率有所提高,且后者的运行时长较前者更短。在采用同种状态识别方法时,使用NGO-VMD和SSNGO-RF算法进行原始振动信号去噪比使用传统的中心频率法准确率高了0.0250,运行时长减少2.21s。

上述实验结果表明,使用NGO-VMD算法对原始振动信号去噪并使用SSNGO-RF算法进行状态识别,与使用中心频率法确定VMD算法分解层数、未优化的RF算法、在故障分类中被广泛使用的PSO-RF算法、未改进的NGO-RF算法相比,模型的整体性能有显著提高,在故障分类中具有更好的应用前景。

3 结论

对风机齿轮箱振动信号故障诊断的相关方法进行研究,提出了NGO-VMD和SSNGO-RF算法。首先采用NGO-VMD算法对风机齿轮箱振动信号进行去噪,并对特征向量进行有效提取;然后采用SSNGO-RF算法对特征向量进行诊断;最后将所提方法与RF、PSO-RF、NGO-RF等算法进行对比实验,验证所提算法的准确率。结果表明:1) 通过NGO算法对VMD算法的分解层数K与惩罚因子α进行确定,有效避免了VMD算法因人工设置参数而出现的过分解或欠分解问题,使用经NGO-VMD算法去噪重构的振动信号,能有效提取特征值并将每组特征值组成特征向量,经实验验证,该方法相比传统采用中心频率法确定VMD分解层数的算法,在后续的故障识别效果与分类准确性方面都有提高;2) 使用SPM混沌映射和SCA方法对NGO算法进行改进,提出的SSNGO算法有效解决了NGO算法中存在的缺乏种群多样性问题,并提高了NGO算法前期的全局搜索能力和后期的局部搜索能力,使搜索过程更加细致;3) 将SSNGO与RF算法相结合对特征分量进行故障识别与分类,并与RF、PSO-RF、NGO-RF等算法对比,证明了所提方法对振动信号的特征向量具有更高的诊断准确率。