池室结构对竖缝式鱼道水力特性的影响

陈柏宇,袁 浩,何小泷,孙 倩,许光祥

(1.重庆交通大学 河海学院,重庆 400074; 2.重庆交通大学 西南水运工程科学研究所,重庆 400016)

0 引 言

近年来,闸坝建筑物等拦河工程在防洪、航运、发电等方面都发挥着巨大作用,但同时也对河流生态环境带来潜在影响,研究表明全球鱼类数量近年来受水利工程影响已减少近30%[1]。竖缝式鱼道能够有效缓解拦河工程所导致的鱼类自然通道阻断等影响,是常见人工构建的鱼类洄游通道型式[2]。依托其独特的结构型式,水流在进入池室后经过扩散、折返对冲作用进行消能,从而形成适合鱼类洄游的流态、湍流水平以及涡强等[3-4],帮助洄游性鱼类上溯。

目前,针对竖缝式鱼道已有大量的试验及数值模拟研究。Rajaratnam等[5-6]先后对18种竖缝式鱼道展开了较为系统的试验,研究内容涉及了隔板型式、坡度、池室长宽比等影响流场的主要因素,同时还提出了池室内无量纲流量与水池中心位置相对水深的计算公式。Puertas等[7]针对竖缝式鱼道的流态开展研究,指出池室内的水流中存在两个典型区域,以较大流速为主要特征的主流区,以及低速和水平涡流共存的回流区。徐体兵等[8]通过数值模拟对11种不同池室长宽比的竖缝式鱼道进行了研究,结果表明在长宽比8∶8～10.5∶8的范围内,可以在各池室内获得有利于鱼类洄溯的流态。董志勇等[9]在不同典型流量的竖缝式鱼道研究中发现,竖缝断面流速呈正态分布,当竖缝主流流速较大时,主流区两侧产生卷吸作用形成漩涡,漩涡强度随着池室内流速增大而增强。罗小凤等[10]对过流流量等水力学指标相同的竖缝式鱼道研究中发现,假设壁面为光滑体,则通过竖缝的主流偏转程度随着竖缝的导向角度增大而增强,但流速也随之发生迅速衰减。Quaranta等[11]对6种不同鱼道底坡坡度条件下池室流场开展系统研究,研究表明,随着床面坡度的增加,竖缝处流速明显增大,低流速回流区则受到高流速区的挤压而减小,而池室内低流速区对于鱼类洄游过程中的休憩至关重要。Li等[12]在对两种隔板型式的竖缝式鱼道研究中发现,不同坡度下相邻池室水位差相等,将不影响竖缝处的流速。

除了前述常见的隔板型式、池室长宽比、坡度等鱼道流场影响因素,在池室内布置圆柱、半圆柱等不同型式的障碍物也是鱼道优化的重要方式之一[13-14]。利用障碍物对竖缝处的水流进行干扰,达到降低最大流速,优化池室内流场分布的效果。因此本研究针对某水利枢纽鱼道,利用数值模拟系统研究了在3%坡度条件下,障碍物的布置位置对池室内流场的影响,并与常规型式的竖缝式鱼道进行对比。

1 数学模型

1.1 模型选择

针对鱼道池室内的复杂流态,Barton与Keller[15]对竖缝式鱼道开展了三维数值模拟研究,并将模拟结果中的水流流速分量和水深变化与相应物理模型试验数据进行量化对比,证明采用流体体积法(Volume of Fluid,VOF)的RNGk-ε湍流模型可以准确获得竖缝式鱼道中各池室的流场信息。该模型通过修正紊动黏度,在ε方程中考虑了时均应变率,能较好地模拟流线弯曲程度较大或高应变率流动。其相应控制方程如下。

连续方程为

(1)

动量方程为

(2)

紊动能k方程为

(3)

耗散率ε方程为

式中:ui、uj分别为沿着xi、xj方向的速度分量(m/s);t为时间(s);g为重力加速度,取9.8 m/s2;ρ为体积分数平均密度(kg/m3);P为修正压力(Pa);μ、μt为黏性系数(N·s/m2)和紊动涡黏系数(N·s/m2),Cμ=0.084 5;k为紊动能(m2/s2),σk=1.39;ε为紊动耗散率(kg·m2/s3),σε=1.39;Gk为紊动能产生项,Gk=μt((∂ui)/(∂uj)+(∂uj)/(∂ui))(∂ui)/(∂xj)。Cε1、Cε2为经验常数,Cε1=1.42,Cε2=1.68。

本研究中多相流自由表面捕捉采用VOF法。VOF法通过在流体域构造流体体积函数来追踪空间网格内的流体体积变化,并据此构造自由面形状。当第q相流体的容积分数αq=0时,表示控制体内无q相流体;αq=1时控制体内充满q相流体; 0<αq<1控制体内充满部分q相流体;对所有流体相的容积分数总和为1。αw的控制微分方程为

(5)

式中αw为水的容积分数。通过求解该连续方程来对水气界面进行跟踪。

1.2 计算模型与网格划分

计算区域包括鱼道进口、鱼道出口及7个池室。每个池室长L=3.1 m,宽B=2.2 m,竖缝宽度b0=0.35 m。数值模拟中鱼道进出口边界分别采用压力进口和压力出口,各池室顶部设置为压力进口,参考压力为标准大气压。上下游运行水深均设为常水深1.5 m。池室内各壁面则设置为无滑移边界。模型网格采用收敛性较好的六面体网格对计算区域进行划分,鱼道设计的网格数量均为200 000左右,同时对竖缝区域进行了局部加密,以更好地反映竖缝流速变化, 如图1所示。本研究中含钩状型竖缝式鱼道,以及3种圆柱型障碍物在池室内的布置方式,如图2所示,圆柱直径D=b0=0.35 m,圆柱位置分别为x=1.5b0,y=3.1b0(距离竖缝中心b0);x=2.2b0,y=3.1b0以及x=3.0b0,y=3.1b0。

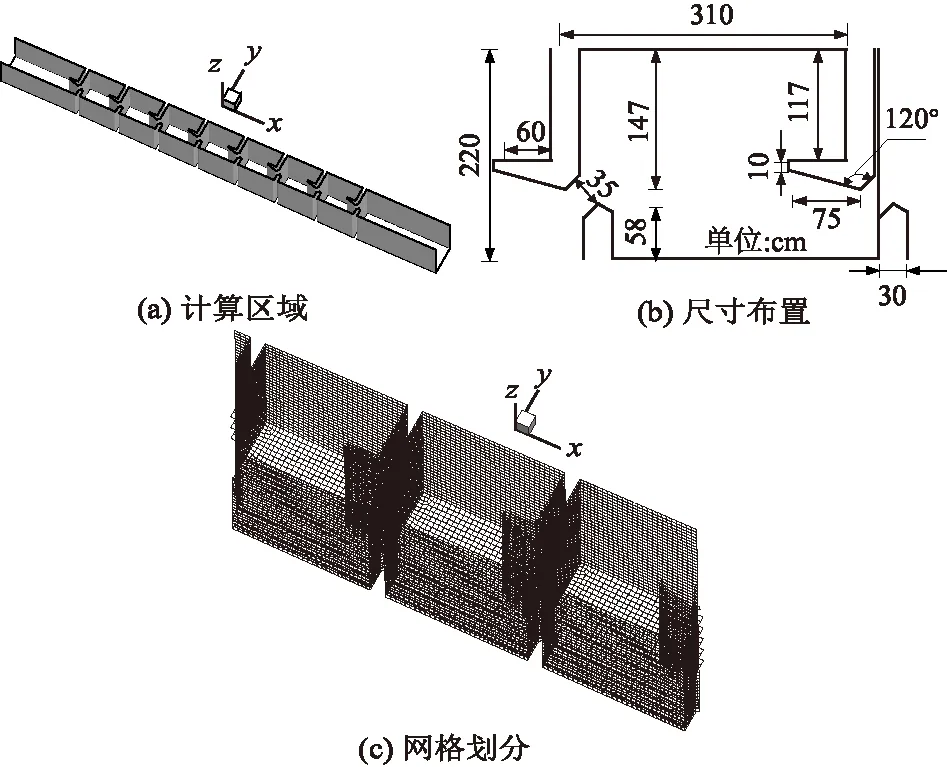
图1 计算区域与网格划分

图2 池室结构示意图

2 模型验证

本研究数值验证所选用试验数据通过某水利枢纽的鱼道局部模型获得,该模型包含12个常规池和1个休息池,模型比尺为1∶5,拟利用休息池上游的7个池室的流场特性对本研究数学模型进行验证,并开展相应的网格密度分析。

该模型包括一个长度为10.26 m的混凝土水槽和水循环供应系统,如图3(a)所示。池室内的流速场采用三维多普勒流速仪ADV进行测量,鱼道模型池室测点布置如图3(b)所示。上游水位由水库中的平水槽控制,下游水位采用溢流板进行控制。为减少上下游边界条件的影响,本研究中选取第4#池室作为典型池室开展验证。

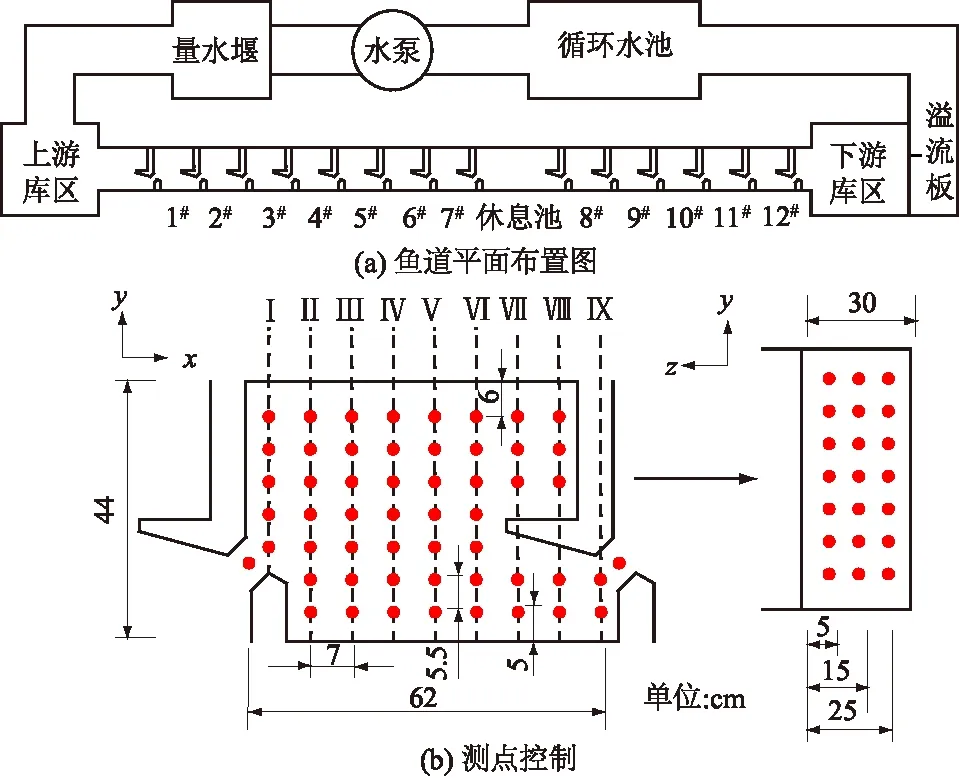
图3 鱼道平面布置图和测点控制

针对模型网格独立性验证,本研究选择3种尺度网格进行试算,平均网格大小、节点数及网格数量如表1所示。典型池Ⅳ号断面测量流速与数值模拟结果对比如图4所示。相对于M2和M3,M1由于网格数量少,导致计算精度偏低,与实测数据偏差较大。而M2与M3的模拟结果相差不大且更接近实测数据,在网格数量满足网格独立性要求的同时考虑计算效率,因此本研究采用平均网格大小为9 cm作为网格密度。

表1 网格独立性验证

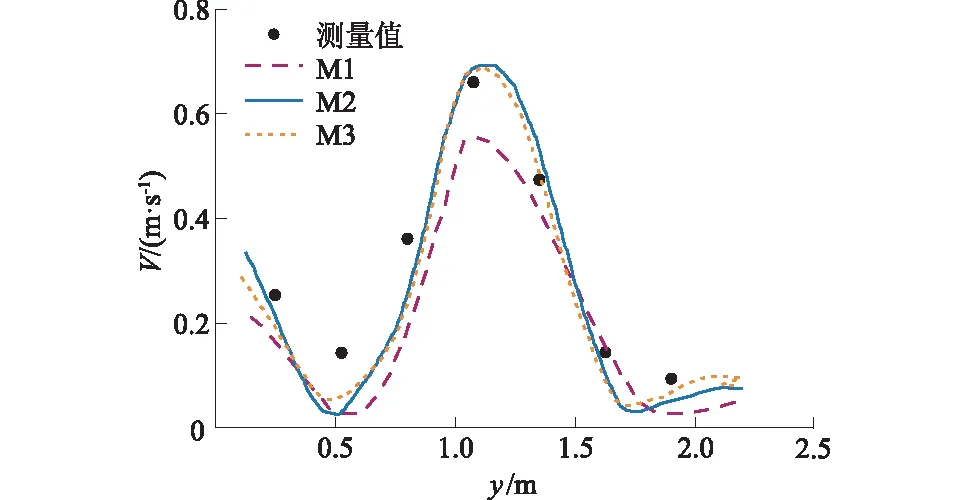
图4 不同网格尺度下断面Ⅳ流速分布与试验对比

典型池中各测点流速的模拟值与测量值对比如图5所示,误差范围取±0.1 m/s。池室内3个平面共156个测量点超过70%的数据在误差范围内,且典型池前后竖缝计算值与测点最大误差仅3.19%(表2),因此可认为模拟结果可靠性满足后续研究需求[16]。

表2 竖缝流速计算值与测量值比较

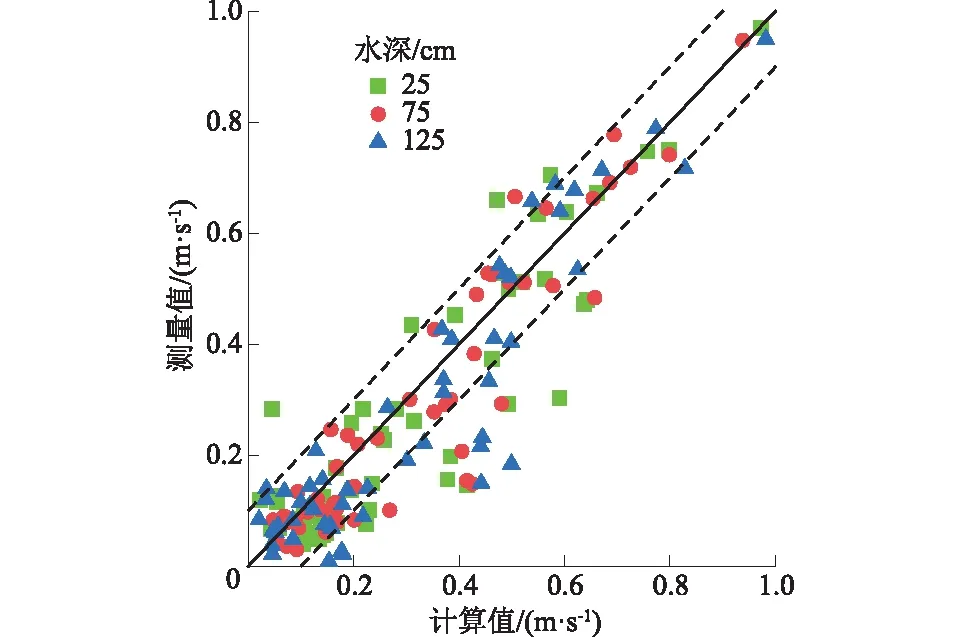
图5 池室流场模拟值与测量值比较

3 结果与分析

为减少上下游边界条件的影响,本研究选取位于中间的第4#个池室作为典型池室。本文所研究对象的坡度均设置为3%,前序研究表明该坡度下池室内流场在垂向上并无显著变化[17],为使流态具有代表性,取距离水面0.5倍水深的平面作为研究对象开展系统分析。

3.1 池室结构变化对流速场的影响

不同结构的池室内流速分布如图6所示。T1是隔板为钩状型的常规竖缝式鱼道,水流经过竖缝压缩,以弯曲形式进入水池流向下一级竖缝,主流两侧存在低速回流区。已有研究[16]表明鱼道中鱼类可辨别较大流速的主流区进行上溯,而主流两侧回流区则为其在洄游过程中提供休憩场所。对于其他3种池室结构,通过竖缝后的高流速水流被圆柱阻碍无法直接进入池室,改变了原本的行进方式。同时主流被圆柱一分为二,在池室内形成不同流态。

图6 池室内流速分布

为便于对比分析障碍物布置对流场的影响,在常规池室平面流场图中标记了3种圆柱布置位置,如图7所示。对于T2布置方式(图6(b)),进入池室的主流被分为两股高速水流,分别流向圆柱左右两侧,并在隔板钩头前汇合。此时圆柱位于主流偏左的位置(图7),水流高流速部分受圆柱阻碍朝池室右侧偏移,其平均流速大于左侧高流速区。圆柱的设置导致右侧高流速区流线弯曲曲率减小,沿程水头损失也随之减小,因此竖缝处流速与T1相比并无显著减小。同时,池室内的低速回流区面积较常规池室减小,且左侧回流区域减小得尤为明显。此外,由于圆柱附近产生的绕流,在圆柱后方形成了小范围的低流速区。T2引起的流态变化导致可供鱼类休息的低速回流区面积减小,可能导致其在上溯过程中无法得到充分的休息,降低过鱼效率。而对于T3、T4两种工况(图6中的(c)、(d)),圆柱同样阻碍了主流的行进,并在圆柱两侧形成绕流,但由于圆柱位置更偏向常规池室的主流右侧,因此高流速水流主要流向了池室左侧区域,类似于“Ω”形,延长了主流在池室内流线,同时池室内右侧出现了一定范围的低流速区。不过,由于T4中圆柱距离竖缝更远,因此通过竖缝后的水流受到干扰相对较弱,主流弯曲程度相比T3更小,同时进入池室后的主流平均流速也更高。

图7 常规池室流场与圆柱位置示意图

作为影响鱼类洄游的关键因素之一,鱼道的最大流速决定着鱼类能否利用自身爆发泳速通过竖缝进入下一池室。4种池室结构的竖缝区域流速,见表3。

以国内鱼道一般采用的允许最大流速1.2 m/s作为上限[12],4种圆柱布置型式的最大流速分别为1.360、1.342、1.196、1.286 m/s,仅有T3达到了鱼类洄游要求。此外,相比于T1,其他布置形式下竖缝平均流速会出现一定的减小。可以看到,尽管T2中圆柱距离竖缝较T3、T4更近,但其对最大流速的影响并不明显,这主要是因为圆柱位置偏向常规池室主流左侧的同时距离长挡板上游面过近,从而迫使大部分高流速水流沿着圆柱右侧进入池室(图6(b)),此时圆柱的位置对于整个池室来说更近似于是竖缝的延伸,因此并不能对水流形成理想的干扰,这一现象与王猛等[14]的研究一致;而在T3、T4中,由于圆柱偏向原常规池室主流右侧,使得高速水流沿左侧进入池室,延长了主流流线的同时引起局部区域水位雍高,有效阻碍了水流流动,使得竖缝区域流速减小;不过,与前文中对流态的影响原因相同,T4的圆柱布置位置对流速的影响较T3来说相对较弱。

3.2 池室结构变化对紊动能的影响

紊动能(TKE)是影响鱼类通过鱼道的重要参数之一,鱼类在高紊动能的湍流中,需要消耗更多的能量来抵抗紊动。同时,高紊动水流还可能延长鱼类成功通过鱼道的时间,影响鱼道过鱼效率。本研究中,紊动能k可定义为

(6)

式中u′x、u′y、u′z分别为纵向、横向和垂直紊动流速。

4种池室结构的紊动能分布如图8所示。在图8(a)中,池室内高紊动能区域仅存在于竖缝附近。在进入池室后,高紊动能区域发生扩散并随之衰减,k>0.01 m2/s2的区域分布面积约为池室面积的75%。相比于常规池室,在池室内布置圆柱后,紊动能分布发生了显著变化。与T1布置相比,T2布置型式中池室内紊动能较高的部分被圆柱限制在其附近区域(图8(b)),同时T1中隔板钩头前侧的较大紊动能区域明显减小。T3在几种池室结构的鱼道中紊动能分布较为理想,竖缝区域和池室内紊动能均<0.02 m2/s2。而T4由于圆柱距离竖缝更远,因此紊动能>0.02 m2/s2的范围在池室内明显相比T3更大,同时,由于隔板钩头对主流的约束增强了紊动,在其附近出现了0.031 m2/s2的极大值。

图8 池室内紊动能分布

Marriner等[18]认为,池室内的紊动能应该保持在0.05 m2/s2以下,否则会影响鱼类洄游。本研究中池室内的最大紊动能及平均紊动能如表4所示。由于坡度较低,因此紊动强度并不高,4种池室结构最大紊动能均没有超过该范围。对于T2来说,尽管圆柱对池室内的紊动能分布和高紊动区域面积有明显的影响,但在最大值与平均值方面与T1接近。与之相比,T3使池室内的最大紊动能和平均紊动能相较于T1分别减少了65.9%、57.1%。T4则由于圆柱位置原因,最大紊动能减小程度弱于T3,而平均紊动能则受隔板钩头附近区域紊动较强的影响没有明显变化。

表4 池室内最大紊动能与平均紊动能

3.3 池室结构变化对单位体积消能率的影响

有研究表明,鱼类一般更喜欢单位体积消能率(E)较低的区域。根据FAO建议[19],鱼道池室内的E不应该超过150～200 W/m3。通常E可以通过下式计算,即

(7)

式中:ρ为水的密度;g为重力加速度;Q为鱼道过流流量;Δh为相邻池室间水头差。4种池室结构对应的E分别为50.47、46.6、46.32、48.44 W/m3,均保持在较低水平。由于坡度相同,因此E差异并不大。

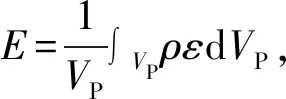
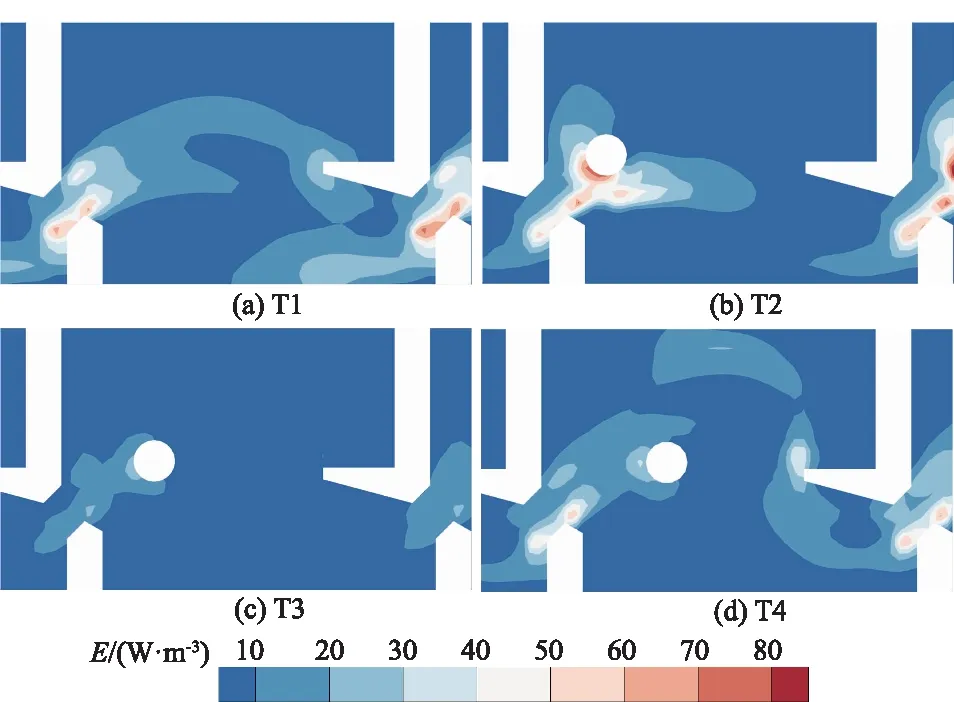
图9 池室内单位体积消能率分布

4 结 论

本文利用数值模拟系统开展不同池室结构对鱼道水力特性影响的研究,对竖缝下游设置阻流圆柱后对池室内流速、紊动能以及单位体积消能率的影响展开分析,得到结论如下:

(1)圆柱位置布置在x=1.5b0,y=3.1b0(距竖缝垂直距离b0)时,竖缝区域的最大流速较常规池室变化较小,射流被圆柱分割为两部分进入池室,供鱼类休息的低速回流区明显减少。而圆柱位置布置在x=2.2b0,y=3.1b0时,通过竖缝的水流得到有效干扰,竖缝区域的最大流速较常规池室减小了12%,在3%坡度下的流速能够满足鱼类洄游要求。池室内的流态受圆柱影响呈“Ω”形,流线曲率增大的同时流程增长,有效增加了池室内沿程水头损失,同时主流右侧形成较大回流区,可供鱼类在洄游过程中休息。当圆柱布置在x=3.0b0,y=3.1b0时,圆柱对池室内流场的改善效果减弱。

(2)在鱼道中布置圆柱可以有效减小紊动能分布范围,当圆柱位置布置在x=2.2b0,y=3.1b0时,池室内的最大紊动能及平均紊动能相较于常规池室分别减少了65.9%、57.1%,能够满足更多鱼类上溯条件。

(3)当圆柱布置在x=1.5b0,y=3.1b0位置时,池室内最大单位体积消能率出现在圆柱前端,达到71.2 W/m3,且高于40 W/m3的分布面积大于常规池室,而圆柱布置在x=2.2b0,y=3.1b0时单位体积消能率在池室内均处于较低水平。圆柱等障碍物的布置不一定都能对鱼道的水力特性起到积极的作用,其位置的选择至关重要。