蜿蜒式鱼道与竖缝式鱼道的水力特性对比分析
刘 辉,郄志红,吴鑫淼
(河北农业大学 城乡建设学院,河北 保定 071001)
鱼道是1 种能够使被拦河建筑(如水闸、大坝等)阻断的江河重新连通,为鱼类提供洄游路径的专门水工建筑物,具有维系江河上下游水生态的作用。鱼道按结构可以分成工程型鱼道和近自然型鱼道。常见的工程型鱼道有竖缝式、丹尼尔式、池堰式和管道式鱼道等。工程型鱼道中的竖缝式鱼道因其流态稳定、对上下游水位变动自适应性强等优点,在国内外工程应用较为广泛[1]。竖缝式鱼道水力特性的研究历史比较早,20 世纪80 年代,加拿大Alberta 大学的Rajaratnam 团队[2-5]结合水工物理试验与室外观测对竖缝式鱼道进行了系统研究,研究表明鱼道池室的长宽比宜适当取值,当长宽比取值1.25 ~1.88 范围内,鱼道内部水流流态稳定。法国的Larinier 等[6]对竖缝式鱼道的池室消能情况进行了试验研究,提出了可以用鱼道水池单位体积消能率来表达竖缝式鱼道中水体的紊动强度。徐体兵 等[7]通过对鱼道模型进行数值模拟计算,得到了竖缝式鱼道水池的长宽比为9∶8 ~10.5∶8、导板长度与水池宽度之比为0.25 ~0.34 的合理区间,可以获得较好流态。张国强等[8]研究了竖缝宽度对水池内水流结构的影响,并给出竖缝宽度的合理取值范围为b/B=0.15 ~0.20(b、B分别为竖缝宽度和池室宽度)。但在实际工程中,一些工程型鱼道的运行效果不佳,如富春江七里垄水电站鱼道、湖南的洣水洋塘水电站鱼道等未能发挥应有作用[9-10]。
随着生态文明和回归自然理念的不断深化,生态水力学不断发展,鱼道等生态补偿技术被积极开发,其中近自然型鱼道得到了国内外越来越多的重视,用于保护水利工程建设中的鱼类资源。例如孙双科、张国强[11]分析阐述了近自然鱼道的设计理念及方法,并提出近自然鱼道由于构建了鱼类所熟知的水流流态,提高了过鱼能力。王猛等[12]对于仿自然型鱼道进出口布置的流态进行了水工模型试验和放鱼试验研究,得到了进出口附近水流条件的合适位置和影响因素。郄志红等[13]提出1 种新型太极式鱼道,通过数值模拟计算和物理模型试验结合的方法,发现新型太极式鱼道能够显著增强鱼道消能减速效果,流态丰富,利于鱼类上溯洄游。李广宁等[14]引入水生植物元素提出1 种仿自然鱼道并进行了物理模型试验和过鱼试验,发现该鱼道水流蜿蜒,流态丰富,鱼类能够顺利上溯。
笔者结合前期工作成果,提出了1 种近自然的旋流式太极八卦鱼道[15],从近自然型鱼道工程设计方面看,水力学特性研究是鱼道设计的关键技术问题,数值模拟技术能够更加细致地研究内部流场的水力学特性。因此,以其简化模型—蜿蜒式鱼道进行水流数值模拟并与相同规模尺寸的竖缝式鱼道数值模拟结果进行对比评价,说明该鱼道体型的合理性。蜿蜒式鱼道的结构布置与竖缝式鱼道相近,但同时具有近自然型鱼道的特点,适用于特定地形条件及运行水头较低的小型鱼道工程。
1 蜿蜒式与竖缝式鱼道数学模型及CFD 模拟
流体运动应满足连续性方程和动量守恒方程,考虑不可压缩流体的紊动情况,建立鱼道的RNGk-ε紊流数学模型,Navier-Stokes 方程下的控制方程[16-19]如下:


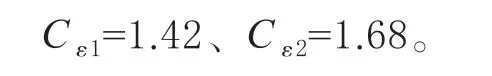
根据鱼道设计准则确定蜿蜒式鱼道和竖缝式鱼道的几何布置参数[20],鱼道结构平面布置图见图1。考虑可比性,设定2 种鱼道的基本尺寸相同,即鱼道的总长、底坡、池室数相同,其它尺寸参数见表1。基于上述数学模型分别对2 个鱼道进行整体模拟。进水口边界设定为压力进口,出水口边界为压力出口,顶部边界设置为压力进口,相对压强设置为0,其余设定为固壁边界。
网格划分:选择六面体结构化网格对鱼道模型进行划分,采用Auto-mesh 功能自适应技术划分网格,网格单元尺寸为0.10 m,网格总数量602 14 个。

图1 蜿蜒式鱼道A 和竖缝式鱼道B 平面布置Fig.1 Plane layout of meandering fishway and vertical slit fishway

表1 鱼道布置技术参数Table 1 Technical parameters of fishway layout
在上游水深为0.40 m 的情境下CFD 模拟的整体结果如图2 所示。可以看到各池室内水流状态基本类似,故下文中取各自的第3#级池室的计算结果进行比较。
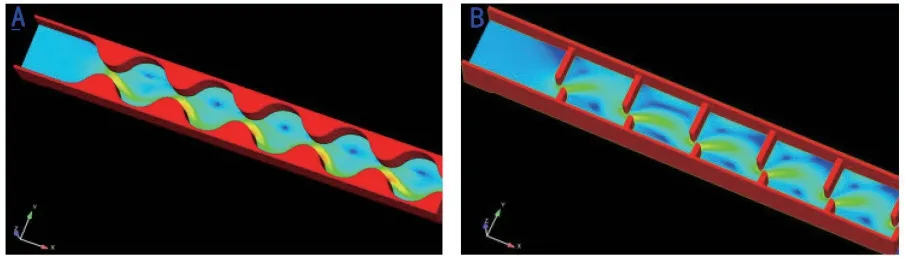
图2 鱼道模拟结果图Fig.2 Simulation results of fishway
2 2 种鱼道水流特性对比分析
2.1 池室流速场分析
分别选取距离鱼道池底H=0、H=0.15、H=0.30 m 的平行于底坡的剖面及其它关键断面,研究鱼道对池室内水流结构不同水深处流速场的影响。
2.1.1 池室不同水深处流速场比较分析 由图3 给出的蜿蜒式和竖缝式鱼道池室3#内距池底H=0、H=0.15 和H=0.3 m 的平行剖面的流场分布可知,鱼道的水流特性有以下异同:
2 种鱼道池室水流特性相似点:(1)主流明确,流态分区明显,有利于鱼类上溯找到正确的上游方向。(2)顺水流方向,2 个垭口或竖缝之间的主流区流速值在纵向上呈现先逐渐减小后增大的规律,在横向上呈现主流区流速高,向两侧流速降低的规律。(3)蜿蜒式鱼道池室中不同水深处(距池底H=0、H=0.15 和H=0.3 m)的流态、流速场分布基本相似,在竖缝式鱼道中也有相同的规律。
2 种鱼道池室水流结构不同点:(1)竖缝式鱼道内,在竖缝处形成了射流至下级竖缝处,且主流小幅度弯曲;而蜿蜒式鱼道的池室内出现旋流,能够产生近似“S”型的水流特征,水流运动蜿蜒曲折,更接近自然河道水流分布,主流弯曲幅度偏大。(2)主流在池室内的相对位置不同。竖缝式鱼道中主流横向上基本位于池室中心区域,而蜿蜒式鱼道中主流大部分分布在池室右侧区域及靠近池壁处,表层主流相对比较扩散,多样化结构形式为不同种群的鱼类提供了更多选择路径。(3)竖缝式鱼道内主流两侧各产生1 个大小不同的漩涡区,对中间的主流造成挤压,使主流更加集中;蜿蜒式鱼道导流坎将急流导向对侧,仅在主流左边产生1 个漩涡区,单侧漩涡对主流挤压偏小,主流相对更加扩散。(4)竖缝式鱼道池室内大部分流速低于1.00 m/s,局部最大流速1.25 m/s 位于竖缝断面边缘处。主流两侧的漩涡区及低流速区流速值在0.38 m/s 以下;蜿蜒式鱼道池室内大部分流速低于1.20 m/s,局部最大流速1.45 m/s 在紧靠垭口右壁位置,范围小,池室左侧区域流速值在0.40 m/s 以下。
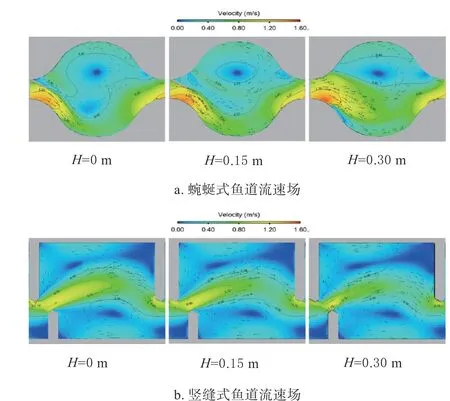
图3 鱼道流速场Fig.3 Flow field of fishway
2.1.2 主流区最大流速轨迹线和沿程衰减情况 图4给出了距鱼道池底H=0.15 m 处蜿蜒式和竖缝式鱼道主流区的最大流速轨迹线,图5 给出最大流速的沿程分布情况。
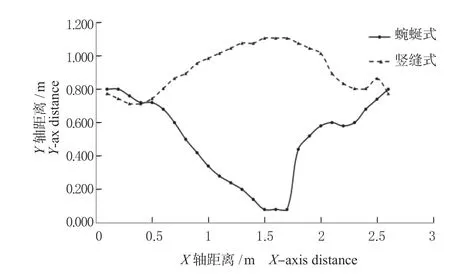
图4 主流区最大流速轨迹线Fig.4 Trajectory of maximum flow velocity

图5 主流最大流速沿程变化Fig.5 Distribution of maximum flow velocity
由图4 主流区最大流速轨迹线图可知,蜿蜒式鱼道主流最大流速轨迹线的弯曲度相比竖缝式鱼道偏大,导流坎的导流作用明显。蜿蜒式鱼道中主流最大流速轨迹线靠右壁弯曲,约在x=1.7 m 处弯曲幅度最大,主流整体分布在池室右侧部分;竖缝式鱼道中主流最大流速轨迹线向左侧略有弯曲,约在x=1.5 m 左右时弯曲幅度达到最大,横向上主流基本位于池室中间位置。
由图5 主流最大流速沿程变化曲线和表2 最大流速衰减率可知,2 种鱼道池室3#中主流最大流速的最大衰减率相差不大,均在55%以上。说明2 种鱼道结构的主流区最大流速沿程衰减明显,变化幅度较大,主流的横向扩散程度较大,均能够有效消减主流能量。
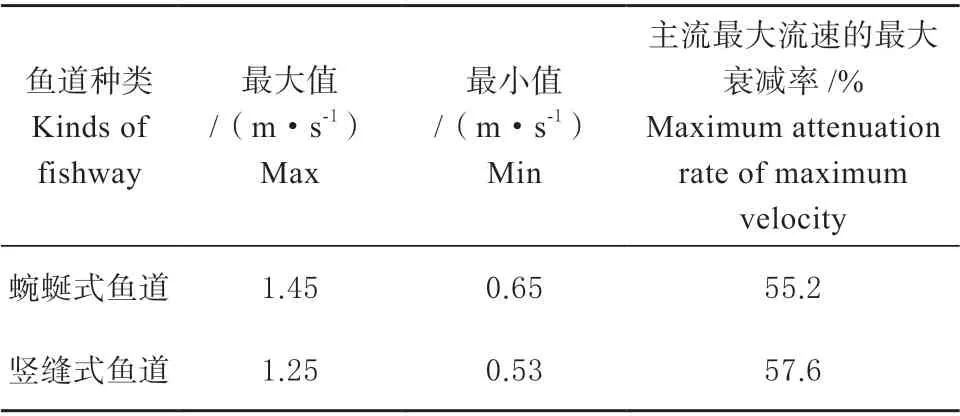
表2 水深H=0.15 m 处主流最大流速最大衰减率Table 2 Maximum attenuation rate of the maximum velocity in the main flow
2.1.3 断面流速分布 垭口或竖缝位置是鱼道结构的最窄区域,也是最大流速出现位置,因此有必要对垭口或竖缝断面流速作出分析。图6a、图6b 分别给出了下层(H=0 m)、中层(H=0.15 m)、上层(H=0.30 m)处蜿蜒式鱼道垭口中心断面流速分布和竖缝式鱼道竖缝中心断面流速分布情况。能够发现,蜿蜒式鱼道垭口中心断面流速在横向上具有明显的梯度分布特点,流速分布范围广,最大流速出现在右侧边壁附近,左侧边壁流速相比右侧边壁偏小,垂向上流速分布基本保持一致,在断面左侧区域流速变化表现明显。竖缝式鱼道竖缝中心断面流速变化在横向上有近导板侧流速偏大,隔板侧流速偏小的规律,垂向上流速分布变化较明显。

图6 断面流速分布Fig.6 Velocity distribution of cross sections
2.2 池室紊动能分析
紊动能即流体紊动所具有的动能,是衡量水流紊动程度的重要指标。紊动能越大,水体湍动程度越剧烈,流体间的碰撞产生的能量损失越大[21]。紊动能不仅影响鱼类的运动能力,还有可能损伤鱼类的身体,对池室紊动能分析十分重要。
2.2.1 不同水深处紊动能分布 图7 给出了距鱼道池底H=0.15、H=0.30 m 处池室3# 紊动能分布情况。对比不同水深处的紊动能分布图发现,蜿蜒式鱼道内同一池室不同深度的紊动能分布情况基本相似,竖缝式鱼道内也有相似的规律。蜿蜒式鱼道主流区的紊动能在0.050 J/kg 以下,池室前端中心位置的紊动能偏大,为0.050 ~0.065 J/kg,两侧池壁附近紊动能最低。竖缝式鱼道池室紊动能分布呈Ω 型,紊动能值为0.036 ~0.106 J/kg,最大紊动能位于竖缝区靠近导板处,左侧漩涡区紊动能范围0.036 ~0.071 J/kg,主流及右侧漩涡区紊动能相对较低。蜿蜒式鱼道的最大紊动能偏小,约是竖缝式鱼道的61.3%。鱼类一般喜于紊动能较低的区域上溯和休息,Silva 等确定了高、低紊动能区的临界值为0.050 J/kg[22]。水流的紊动程度与鱼类的游泳能力呈负相关,紊动能越大,就会越抑制鱼的游泳能力[23]。蜿蜒式鱼道池室大部分区域为低紊动能区,主流区紊动能值TKE<0.050 J/kg,对鱼类的游泳能力及上溯行为影响也相对较小。
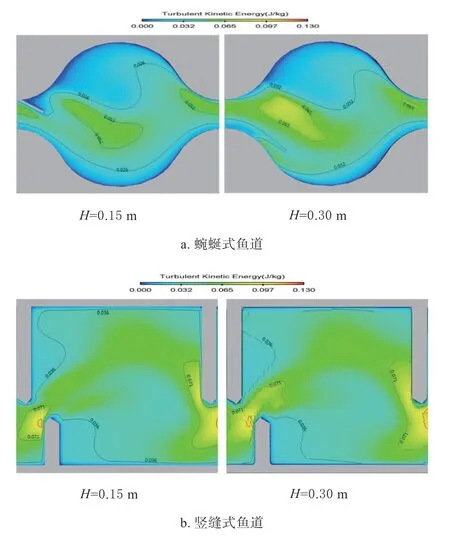
图7 池室紊动能分布图Fig.7 Turbulent energy distribution of the pool
3 结论
应用CFD 模拟计算的方法分别对蜿蜒式和竖缝式鱼道相关的水力特性问题进行了研究分析,得出以下结论:
(1)2 种鱼道结构的流态分区明显,主流明确。蜿蜒式鱼道池室内不同水深位置(距池底H=0、H=0.15 和H=0.3 m)的流态、流速场分布基本相似,在竖缝式鱼道中也有相同的规律。与竖缝式鱼道相比,蜿蜒式鱼道池室内出现旋流,产生近似“S”型的水流特征,水流运动蜿蜒曲折,更接近自然河道水流分布,主流弯曲幅度偏大。
(2)主流在2 种鱼道池室内的相对位置不同,多样化结构形式为不同种群的鱼类提供了更多选择路径。竖缝式鱼道内主流两侧均产生漩涡区,造成对中间的主流挤压,使主流更加集中,而蜿蜒式鱼道导流坎将急流导向对侧,仅在主流左边产生1 个漩涡区,单侧的漩涡区对主流挤压偏小,因此主流更加扩散。蜿蜒式鱼道最大流速出现在垭口及导流坎附近,竖缝式鱼道最大流速在竖缝处,最大流速相差不大,且最大衰减率没有明显差距,均在55%左右,满足过鱼要求。
(3)蜿蜒式鱼道内不同水深处的紊动能分布情况基本相似,竖缝式鱼道内也有类似规律。蜿蜒式鱼道最大紊动能相对偏小,仅是竖缝式鱼道的61.3%。蜿蜒式鱼道池室大部分区域为低紊动能区,主流区紊动能值TKE<0.050 J/kg。
(4)竖缝式鱼道在竖缝处的急缩急扩产生了较大局部水头损失,使竖缝处的最大流速相比蜿蜒式鱼道偏小,但水流紊动偏大,主流位置居中。蜿蜒式鱼道在垭口处是渐缩渐扩,水流更加平顺,紊动较小,池室主流靠近池壁,水流急缓深浅分区。
蜿蜒式鱼道作为1 种近自然型鱼道,池壁结构平滑过渡,与水流运动贴合,更接近自然河道,形式美观,与河流生态相得益彰,但其细部构造优化、底坡J调整和实际工程实施等问题仍需深入探索。

