非稳定渗流条件下宽级配砂砾土细粒迁移试验研究
董 辉,任佳展,程子华,徐 平,蒋秀姿
(湘潭大学 土木工程学院, 湖南 湘潭 411105)
0 引 言
自然地表常见的堆沉积土石混合体,由于组成物质和赋存环境的复杂性,其渗流失稳机理引起了众多关注。大部分研究认为在渗流过程中细粒的侵蚀迁移导致了土体渗流场的改变,导致土体失稳。Wan等[1]通过研究认为间断级配土、宽级配土或砾石含量超过60%中比较容易出现这种渗流侵蚀的现象。Cui等[2]通过人工降雨试验发现汶川地震后形成的松散滑坡堆积体在渗流作用下容易发生内部侵蚀,进而诱发频繁的滑坡和泥石流。在降雨入渗的条件下,Zhang等[3]发现粗粒土中的细粒会由于孔隙流体的作用从土体结构中分离,并且在由粗颗粒构成的基体的孔隙中从坡顶运移到坡脚。周小军等[4]进行水槽试验,认为水力环境是细颗粒发生运移的主要控制因素,入渗过程的时长与强度都对细颗粒起动具有决定性影响。姚志雄等[5]进行垂直渗透砂土管涌试验,使用显微设备观察试样中细颗粒运动状态,研究不同颗粒级配对试样内部稳定性及渗流特征的影响,发现土体的内部稳定性与级配曲线形状与级配不均匀系数有关。
土体中细粒的稳定程度是土体渗流失稳是否发生的重要判定条件。目前,有多种方法通过材料的几何与组构特征土体内部稳定性进行判断评价,通过不同的控制变量对介质内部稳定性进行分析。这些方法中,一部分只考虑介质本身单因素对内部稳定性的影响,如Istonima准则[6]、Kezdi法[7]和Kenney&Lau法[8]等。一部分考虑介质本身多个因素影响,如Burenkova法[9]与Wan&Well法[1];此外,还有Andrianatrehina法[10]通过试验前后参数变化内部稳定性进行分类。然而大量的渗透侵蚀试验未准确地给出判定内部稳定性的标准[11-14]。研究受限于试验中的易获取的参数指标,对内部稳定的判断多是通过试验后分区域筛分确定细颗粒迁移量或是通过细颗粒流失量进行间接判断;可视化方法受土体本身的不透明特点影响,仅限于对表观颗粒运动现象的观察。
本文通过标准石英砂(熔融石英砂)配制不同参数透明宽级配砂砾土,利用圆柱入渗试验装置进行可观察内部细粒迁移特征的渐进水力梯度入渗试验,采集渗流速度、质量侵蚀率等参数,研究侵蚀率对各因素的敏感性差异,并通过观察到的细粒迁移特征结合宏观参数变化特征对试样进行内部稳定分析,对已有内部稳定性准则判断结果进行比选后结合试验结果进行修正。
1 材料与方法
1.1 试验材料与试样装置
1.1.1 试验材料
为了便于直接观察渗流过程中细粒迁移发生的沉积堵塞等特征。采用标准石英砂配置砂砾土,基本物理参数如表1,将粒径<0.25 mm的颗粒作为细粒分类,并进行染色处理以加强对比效果(见图1)。

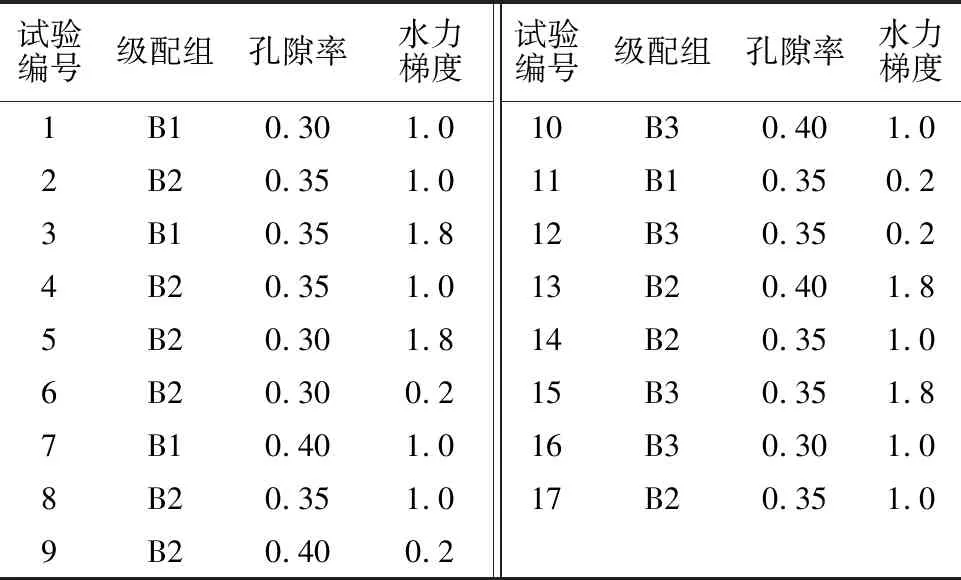
表1 标准石英砂参数
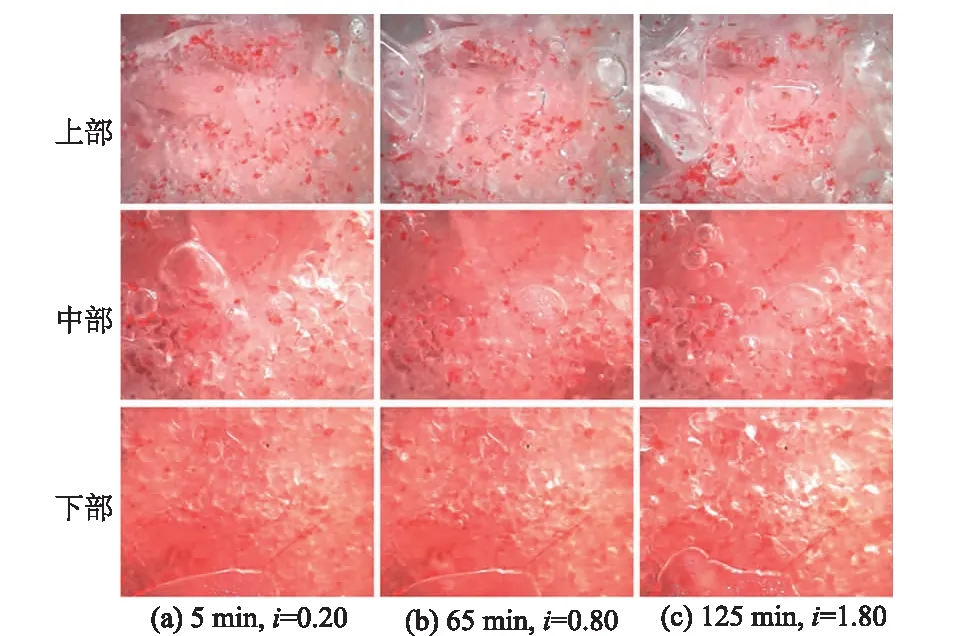
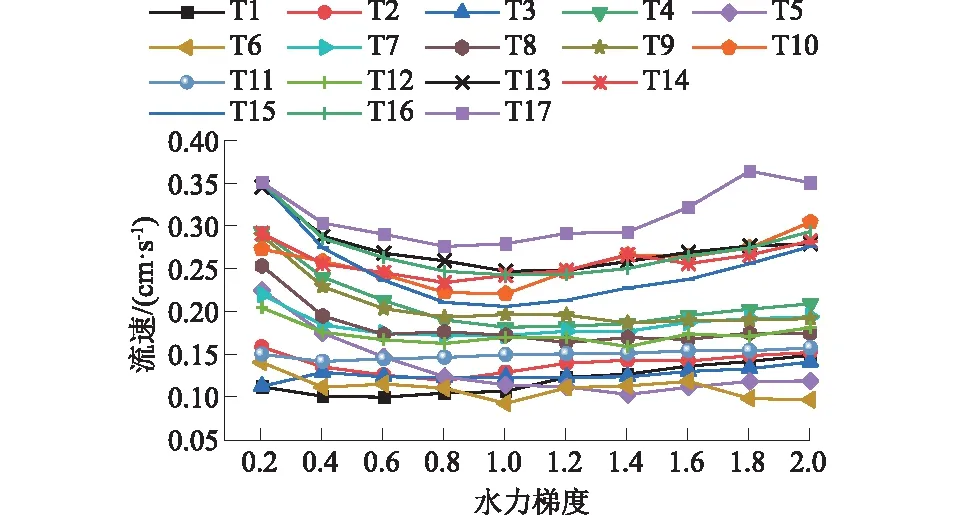
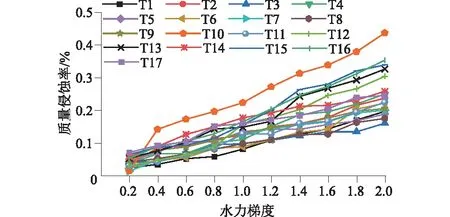
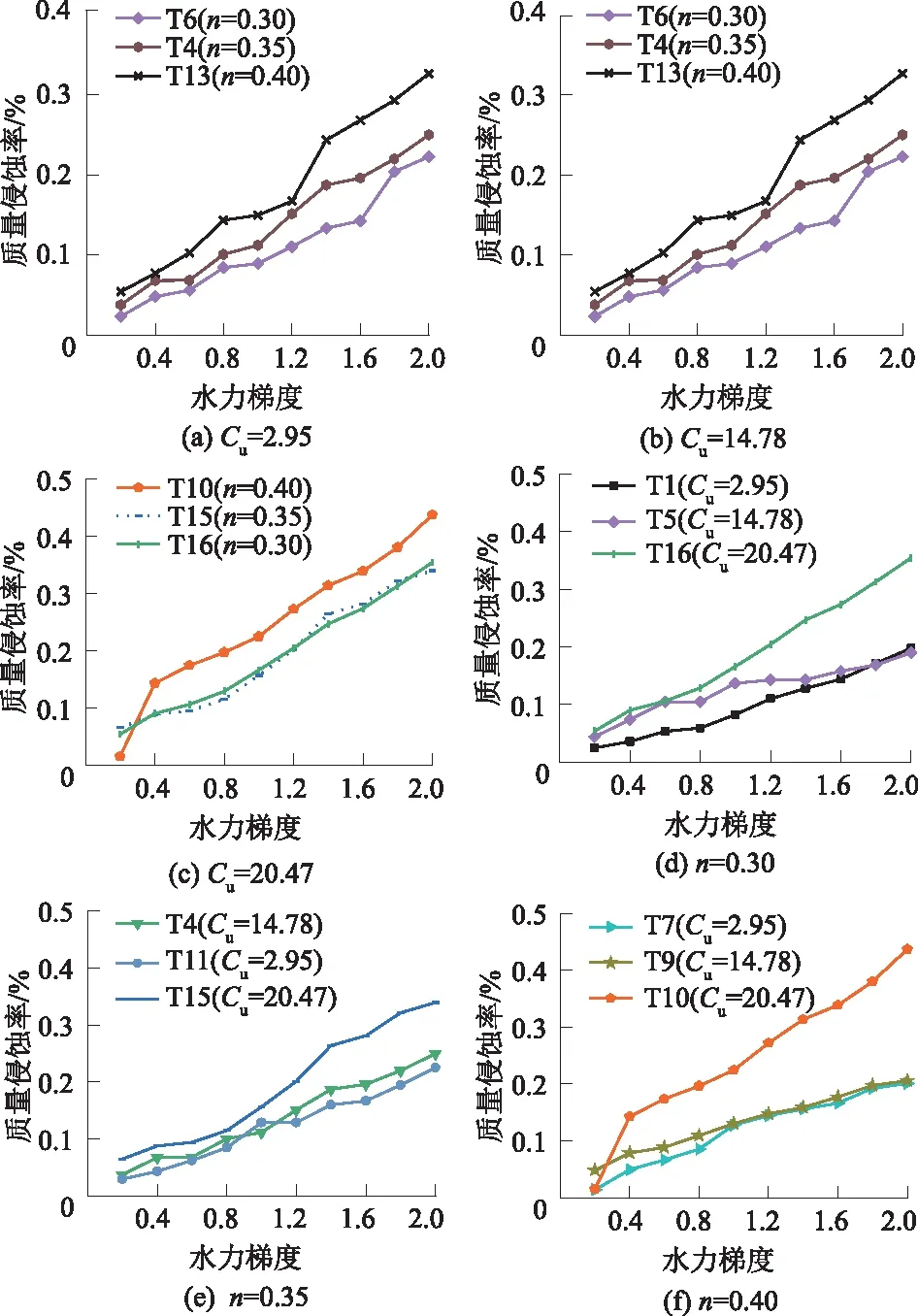
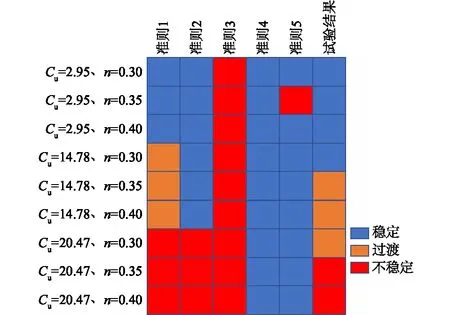
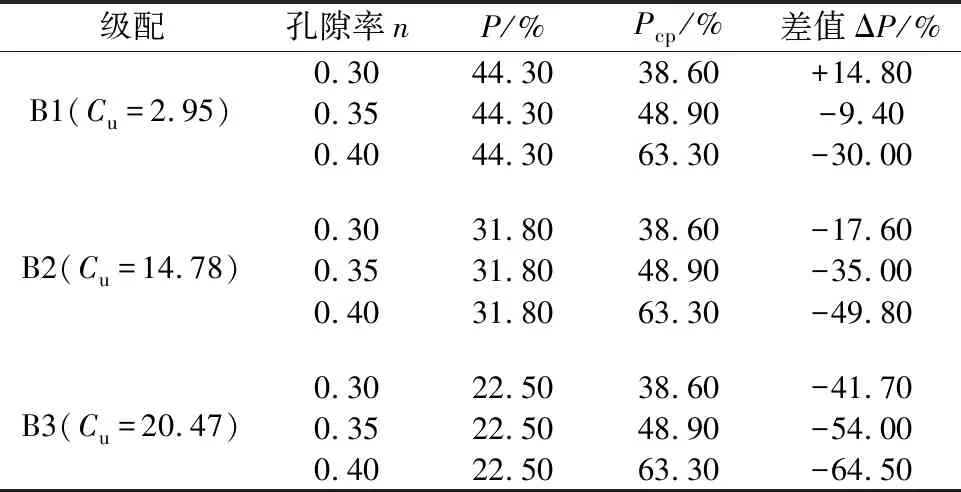
级配不均匀系数是判断土体渗透变形类型的重要指标之一,部分规范中[15]认为不均匀系数Cu≤5时,土样产生的渗透变形形式是流土。屈智炯[16]总结认为土样渗透变形模式在Cu≤10时为流土;5 1.1.2 试验装置 采用自行设计的圆柱入渗试验装置,模拟不同水力梯度下垂向渗流侵蚀作用。该装置主要由指定梯度供水装置、试样侵蚀容器、侵蚀颗粒及渗水收集装置、视图采集设备四部分组成(图3)。 图3 试验装置示意图 指定梯度供水装置由水箱和溢流管组成,通过改变溢流管口高低控制水头大小。在此装置中,在筛网顶部设置2 mm的粗砂砾作为缓冲垫层。试样侵蚀容器由透明亚克力板材制作,其尺寸为内径10 cm、高度25 cm的圆柱。在保证必要刚度的同时具有良好的视觉效果,可以通过摄像设备观察到内部颗粒状态。侵蚀颗粒及渗水收集装置由塑料桶和量杯组成,经沉淀后细颗粒沉积于杯底,出渗水流入大桶收集。 视图采集设备分试样整体图像与显微图像。整体图像采集使用常规CMOS数码摄像头,参数值:500万像素;最大帧率30帧/s。显微图像采用USB显微相机进行采集,最大放大倍数500倍;最高采集频率为25帧/s。 1.2.1 试验设计 本文采用响应面试验设计方法,分析试验因素与质量侵蚀率(细颗粒流失量占总颗粒质量的百分比)的相关性,选取级配不均匀性系数(Cu=2.95、14.78、20.47)、孔隙率(n=0.30、0.35、0.40)及水力梯度(i=0.2~2)作为影响因素,利用试验设计软件Design-Expert得到试验工况组见表2。 表2 试样侵蚀试验工况设计 1.2.2 试验流程 ①按照试验设计进行制样,分五层进行击实,使试样达到设计的干密度;②布置上中下3个显微观察点,位置分别为4、12.5、21 cm处,间隔5 s一次采样,以观测内部颗粒运动过程;③按实验计划水头,垂向入渗,对出水定时收集称重计量,流失颗粒逐级收集称量;④将沉淀池整体取出烘干,计量增加质量。 根据显微图像(由于篇幅原因,仅仅展示T15组(Cu=20.47、n=0.35),见图4),发现随试样参数的变化,内部细粒活动的活跃程度存在明显差异。对各试验组内部细粒运动状态做出统计并分析不同试样组按细粒活跃程度划分为无颗粒运动、个别颗粒沿渗流通道运动(细分为原位振动荡、短距离迁移、脱离观察范围3种)及大范围颗粒运动3种。对运动状态程度从大到小赋值为1~5,结果绘制于图5。将试样内部细粒稳定程度划分为3个阶段:稳定段、过渡段、不稳定段。其中处在稳定段的试样中细粒无明显运动或在原位运动,对试样内部孔隙大小形状几乎无影响;过渡段试样中个别细粒发生短距离迁移改变,改变了试样局部的孔隙形状大小;而处在不稳定段的试样内部细粒迁移发生大规模运动或长距离迁移,导致试样整体孔隙结构改变。 图4 T15组各观测点示踪细粒运动 图5 细粒运动状况统计 可见不同组试样中细粒运动活跃程度,随级配不均匀度及试样孔隙率增加,内部颗粒的不稳定性逐渐增大。各项因素中单一指标不具有明显的主要控制作用,在各因素综合作用下,试样骨架颗粒间可能形成更大的孔隙,细粒与骨架结构更加不稳定易形成破坏。 在各组试验中,对出水量进行计量,计算出各试样不同水力梯度下的出流速度(见图6)。分析发现,各组试样中出流速度分布在0.092~0.365 cm/s之间;除T3、T11组之外,试样在较小水头入渗的初期阶段都存在流速随水头增加而减小的渗透压密现象,在水头增加至某一特定值后,流量随水头增加而波动变化。 图6 流速-水力梯度关系 在梁越等[17]、陈亮等[18]、陈建生等[19]研究中也存在此类渗流性波动的现象,主要是由于内部细粒发生迁移,导致局部孔隙分布变异,进而影响到整体渗透性的波动。在垂直入渗试验中,受重力与渗流方向的影响,细粒运动规律受重力与水力及孔喉形态特征控制,具有随机性,但根据实际工程统计,如果不发生较大规模的渗透变形,与试验条件相似的现场中[20-21],存在“渗透压密”现象。可见,渗流突变点位置对其自滤过程中侵蚀-重排列-淤堵过程有重要影响,决定其内部是否发生大规模渗流变形,最终导致土体整体变形破坏。 因此,线性拟合各组流速对应水力梯度关系得到渗流突变点信息,见表3。分析发现,对于B1级配(Cu=2.95)下,孔隙率为0.30与0.35的试验组,其渗流突变点出现时的水力梯度为不存在或明显小于其他组别,为0.380~0.612之间,而其他试验组渗流突变点处水力梯度在0.705~1.246之间。 表3 不同因素下渗流突变点统计 这表明级配不均匀系数越小,试样密实度越高,渗流突变点出现越早,甚至不出现。渗流突变点的出现与试样内部的渗流变形能力相关,当不均匀性较大时,内部大颗粒形成骨架结构,有效孔隙及可动颗粒活动空间较大,流速发展变异性较大。对于B1级配(Cu=2.95),级配不均匀系数较小,粒间接触相对紧密,当密实度较大时内部结构稳定,在水力作用下孔隙结构变化较小,流速发展较为平稳,所以渗流突变点不明显。 质量侵蚀率是土体内部稳定的重要判断条件,试验中收集流失细颗粒并计算出质量侵蚀率绘制于图7。从图7可见,水力梯度在0.2~2.0时,各组侵蚀率差异性相对较小,但整体随不均匀系数及孔隙率的增加而增加。因此,对不同级配同孔隙率和同孔隙率不同级配试验结果进行分析。 图7 质量侵蚀率-水力梯度关系 从图8可见,对B1级配(Cu=2.95),孔隙率为0.30的T1组侵蚀率最小,孔隙率为0.35与0.40的T11和T7组侵蚀率差异不大,从侧面反映了:在不均匀度系数较小级配介质中密实度更高的内部结构更不易破坏,细粒不易受到侵蚀;随孔隙率增大到某一临界孔隙率时,内部颗粒流失就与孔隙率变化关联性减小,与可流失细粒占总质量比例关联性增大。对B2级配(Cu=14.78),孔隙率为0.30的T6组侵蚀率最小,孔隙率为0.40的T13组侵蚀率相对发展更快,数值更大。从侧面反映了:在不均匀度系数为14.78的试验组中密实度更高的试样其内部结构稳定性更强,细粒不易受到侵蚀;随孔隙率增大,质量侵蚀发展越来越活跃,明显高于孔隙率较小方案组。对于B3级配(Cu=20.47), T15与T16质量侵蚀率比较接近,孔隙率为0.35的T15组前期侵蚀率较小,在水力梯度增长到1.2后,超过孔隙率为0.30的T16组,但差别不大。孔隙率为0.40的T10组质量侵蚀率相对发展更快且侵蚀率最大。 图8 不同因素下质量侵蚀率-水力梯度关系 对于孔隙率为0.30试验组,级配为B1(Cu=2.95)和B2(Cu=14.78)的T1与T5质量侵蚀率比较接近。级配为B3(Cu=20.47)的T16组质量侵蚀率相对发展更快且侵蚀率最大。对孔隙率为0.35试验组,级配为B1和B2的T11与T4质量侵蚀率比较接近。级配为B3的T4组质量侵蚀率相对发展更快且侵蚀率最大。对于孔隙率为0.40试验组,比对3种不同级配试样的质量侵蚀率,级配为B1和B2的T7与T9质量侵蚀率比较接近。级配为B3的T10组质量侵蚀率相对发展更快且侵蚀率最大。 由此推知,级配不均匀系数影响细粒流失的发展过程。不均匀度系数较小级配介质中,孔隙率越小即密实度更高的,其内部结构更不易破坏,细粒不易受到侵蚀;随孔隙率增大,当到达临界孔隙率时,内部颗粒流失就与孔隙率变化关联性减小,与可流失细粒占总质量比例关联性增大。 通过Design-Expert软件对试验结果数据进行响应面分析,得到各因素对侵蚀率的影响由大至小依次为:水力梯度、级配不均匀度、孔隙率。计算出理论上侵蚀率最大的组别:即在Cu=20.47、n=0.4的试样在i=2.00下侵蚀率最大,为1.233%。 目前,大部分方法通过材料的几何与组构特征对颗粒堆积体的内部稳定性进行判断评价,通过不同的控制变量对介质内部稳定性进行分析。这些方法中,一部分只考虑介质本身单因素对内部稳定性的影响,如Istonima准则、Kezdi法等;一部分考虑介质本身多个因素影响,如Burenkova法与Wan&Fell法;此外,还有Andrianatrehina法通过试验前后参数变化内部稳定性进行分类。将各判定准则控制变量及判定指标列于表4。 表4 土体内部稳定性判定准则控制变量及指标 根据细粒运动状态结合渗流突变点位置,对各组试样内部稳定性做出判定,并使用现有判定准则对试验所用材料进行判断,判断结果见图9。 图9 多种判定准则判断结果 各方法对内部稳定性判断具有差异性,甚至会给出截然相反的结果。如Burenkova法与Wan &Fell法。Burenkova法趋于保守,将所有组别都判为不稳定;Wan &Fell法趋于激进,所有组别都判为稳定。判定准则判断结果与实际出现偏差。如Kezdi准则将Cu=2.95、n=14.78的组别都判为稳定,然而实际试验中细粒出现迁移,Andrianatrehina方法仅仅将Cu=2.95、n=0.35的T3组判为不稳定,而实际试验中,T3(Cu=2.95、n=0.35)组从显微图像上观察无明显颗粒运动。 综合多种准则判断结果,Istonima准则判断结果相对准确,各准则产生判断偏差是由于: (1)判据不充分,只考虑一种主要因素进行判断,忽略了次要因素对内部稳定性的影响,造成判定准则精确度下降。例如大部分判定准则都是提取颗粒级配参数或直接根据试验结果进行判断,比如孔隙率对内部渗流场影响较大,但在大部分判定准则都考虑较少。 (2)多数判断方法以直接或间接指标对介质进行判断,直接方法采用被侵蚀细颗粒的流出量进行稳定性判别;间接方法通过渗流特征的变化进行判别。值得注意的是,内部细粒在水力作用下产生运动甚至长距离迁移并不意味着一定能够,内部结构复杂,孔喉内径较小孔隙迂曲度高的试样可能会存在细粒的滤积效应,通过侵蚀量判断存在偏差;渗流特征可间接反映土体内部情况,但其与内部稳定关联的量化指标需要进一步明晰。 通过对已有内部稳定性判定准则进行总结并将已有试验参数与结果带入各准则进行比选认为在考虑级配特征的同时,需要引入考虑孔隙率对稳定性进行辅助判断。分析发现仅引入孔隙率对准则进行修正时,对内部稳定状态的划分指标不够明确,故引入最优细粒含量(颗粒骨架内部孔隙被填满时细粒的含量)这一与孔隙率正相关的参数辅助判别。当细粒颗粒含量P大于最优细粒含量Pcp时,细粒可作为骨架承受堆积体渗透作用,超过临界水力梯度后或产生整体性变形;反之,水流的渗透力则主要由粗颗粒组成的骨架承担,细粒沿孔隙渗流通道运动。 Pcp=(0.30+3n2-n)/(1-n) 。 (1) 式中Pcp为最优细粒含量。 根据《水利水电工程地质勘察规范》(GB 50487—2008)推荐公式(式(1))计算不同孔隙率n下最优细粒含量Pcp与试样实际细粒含量P,见表5。 表5 不同级配与孔隙率下Pcp与P对比 需要说明的是表5中最优细粒含量Pcp部分超出了式(1)的应用条件值。但是在对数据分析后发现,除组合Cu=2.95、n=0.30细颗粒含量P大于最优细粒含量Pcp外,其余各组均不同程度的小于Pcp。各组中Cu=20.47、n=0.40差值最大,该组内部细粒活动空间最大,内部稳定性最差,此类现象在试验中也得到印证。可见,最优细粒含量与实际细粒含量的差值绝对值∣ΔP∣与试样内部稳定呈正相关,表明通过式(1)将孔隙率换算为最优细粒含量,利用∣ΔP∣对Istonima准则修正可行,修正后结果见表6。 表6 修正Istonima准则 通过引入孔隙率与不均匀系数综合判定土体内部稳定状态,较单一参数判别更为充分,进一步实践应用将使之趋于完善。 (1)试验中细粒活跃程度随不均匀系数和孔隙率的增加而增加。可划分为稳定、过渡和不稳定3个阶段。稳定段的试样中细粒无明显运动或在原位运动;过渡段试样中个别细粒发生短距离迁移改变,不稳定段的试样内部细粒迁移发生大规模运动或长距离迁移。 (2)试验中流速发展过程存在明显渗流突变点。该渗流突变点是渗流压密—渗流侵蚀的转化临界点,低于临界梯度时试样渗透压密且渗流过程平稳,高于临界梯度时,内部结构破坏导致渗流与侵蚀过程波动发展。不均匀系数、孔隙率等参数对试样内部细粒的运动稳定性呈正相关。通过对响应面试验组进行分析,质量侵蚀率敏感性从大至小为水力梯度、级配不均匀度、孔隙率。 (3)各内部稳定性准则中Istonima准则判断结果相对准确,各准则出现偏差的主要原因是判据不充分,且不能观察到土体内部细粒运动状态,通过间接指标判定内部稳定性;通过引入孔隙率n对Istonima准则进行修正,能更准确的判定试样内部稳定状态。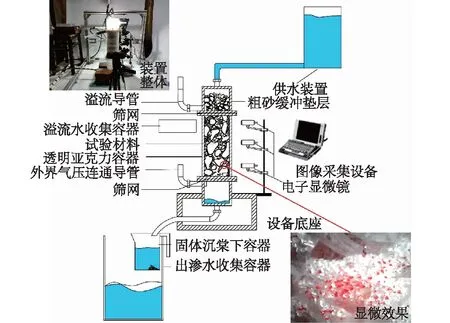
1.2 试验设计及流程
2 试验结果与分析
2.1 细粒迁移特征

2.2 流速变化特征

2.3 质量侵蚀率变化及敏感性分析
3 内部稳定性分析
3.1 判定准则比选

3.2 Istonima判定准则修正

4 结 论

