风电叶片的等效模型建立*

赵鹏礼，张 屹

（常州大学机械与轨道交通学院，江苏 常州 213000）

0 引 言

风电叶片是风电发电机组重要的组成部分［1］，其在工作中主要受到风力载荷的影响，叠加结冰或者风向突变，严重时会导致叶片产生的振动超出界限，从而会发生折断损坏。因此，对风电叶片的振动控制受到了广泛的研究。程危危等人［2］将叶片简化为以恒定角速度绕定轴旋转的不可伸长的等截面欧拉伯努利悬臂梁，采用一维动量叶素理论建立了风力机叶片的空气动力学模型；乔印虎等人［3］基于自适应滤波器，用等截面悬臂梁代替叶片，在其表面粘贴压电元件，完成了悬臂梁的振动主动控制实验。然而，叶片本身结构形状较为复杂，其结构呈固定端宽，自由端窄的特点。直接用实体模型计算比较繁琐，而等截面悬臂梁与实际叶片有较大的差距，并不能完全替代真实叶片进行研究。

因此，本文将风电叶片等效替代成变截面欧拉伯努利梁，基于质量分布相近原则，建立叶片的等效模型，为叶片的振动控制研究奠定基础。

1 模型简化方法

准确的模型在进行动力学分析时尤为重要［4～6］。为了使简化的变截面梁模型与真实叶片模型能够等效，根据质量分布相近原则［7，8］，必须要保证简化的模型的质心与真实叶片模型的质心重合，如图1为等厚度变截面悬臂梁，其截面呈线性变化。

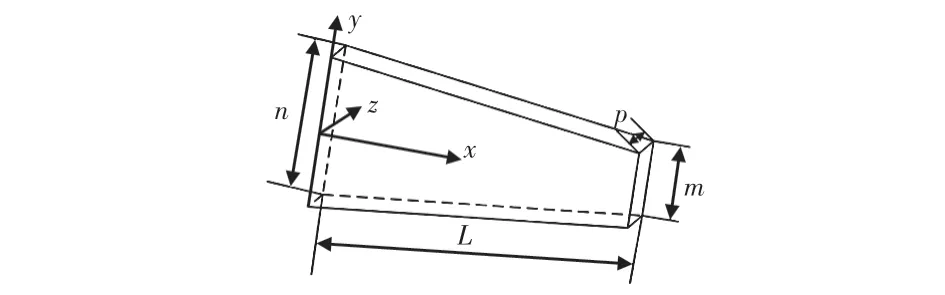
图1 变截面悬臂梁

图1中，n为梁固定端横截面宽度，m为梁自由端横截面宽度，L为梁的长度，p为梁的厚度；x，y，z为建立的坐标系。

根据简化模型与真实模型质心重合可得

式中a为质心位置。

整理可得

所以有

等效模型应与真实模型的刚度分布曲线相近［9］，所以令等效模型与真实模型在质心处具有相同的挠度，有如下表达式

式中Q1为等效模型的质心处的挠度，Q2为真实模型的质心处的挠度。

变截面梁xj位置的抗弯刚度为

式中E为叶片的弹性模量，Ij为xj位置截面的惯性矩。梁上均布载荷为1时xj处的弯矩M（xj）为

一段叶片的转角vi为

则xj位置的转角wj为

一段叶片的挠度si为

则xj位置的挠度Q1为

由等效模型和叶片模型质量相等得到

式中 ρ为叶片材料密度，M为真实叶片质量。

把式（2）代入式（11）可得

由于E，ρ值由叶片材料决定，其通常为玻璃纤维制成，根据式（4）和式（10）可以确定等效的变截面悬臂梁的尺寸。

2 变截面梁的刚度和质量矩阵

本文将等效模型视作欧拉伯努利梁［10］，如图2，将变截面悬臂梁等分成宽度为h的多段梁，每段梁近似看作等截面梁。

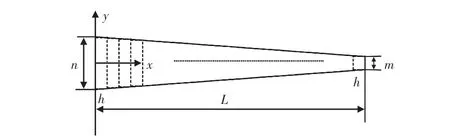
图2 变截面梁等分

根据振动学理论［11］，叶片的能量主要集中在低阶模态中，而低阶模态时叶片振动状态表现为挥舞，因此，只考虑弯曲的等截面欧拉伯努利梁单元刚度矩阵为

将单元刚度矩阵叠加，组成整体刚度矩阵为

由于梁左端固定，故整体刚度矩阵改为

同理，建立单元质量矩阵为

将单元质量矩阵叠加，组成整体质量矩阵为

3 算例分析

3.1 挠度计算

本文以功率为11 kW的风电叶片为例，从翼型软件中导出翼型坐标，利用三维制图软件建立了真实叶片模型，如图3。在叶片表面添加均布载荷1 N，即相当于在其中部添加集中载荷为5 N，将右端叶根固定，通过有限元软件仿真计算，其模型分析结果：弹性模量E为68.9 GPa，密度ρ为2 520 kg／m3，质量M为202 kg，长度L为5 m，质心位置a为0.35 L，质心挠度Q2为2.6 ×10-5m。

图3 叶片模型

将叶片模型分析结果代入上式计算，得出简化的等效变截面悬臂梁参数：截面宽度n为680 mm，截面宽度m为36 mm，厚度p为45 mm。

叶片模型和等效模型的挠度曲线如图4。从图4 中可以看出，叶片模型和等效模型在质心1.75 m处的挠度曲线重合度较高。

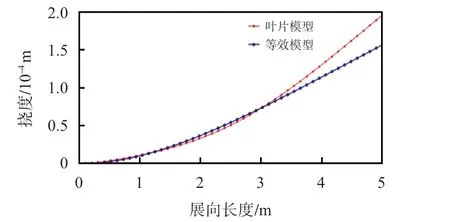
图4 挠度曲线

3.2 模态频率计算

针对复杂的风电叶片结构，能够可靠反映结构特征和动力学特性的相似模型是振动控制系统设计、分析及控制性能评估的基础。依据等效模型的参数尺寸，基于有限单元法［12～15］建立叶片结构动力学参数化有限元模型。表1给出了叶片模型、等效模型和仿真动力学模型的低阶模态比较，结果表明3 种模型相似度较高，仿真自编程序有效。

表1 模态比较

4 结 论

本文针对11 kW的风电叶片的模型参数，基于质量分布相近原则建立了其等效模型，并且对于叶片模型、等效模型和仿真模型的动力学模态进行了比较。结果表明，建立的等效模型能够近似替代真实叶片模型，为风电叶片的振动控制研究奠定了基础。