生鲜肉品冷链配送最短路径算法的构建与应用

王小辉 洪瑾芳 许海林 刘春秀 杨得胜 史 惠 陈冬群 郑丽英

（1.永泰县农业农村局 福州 350700；2.福建省动物疫病预防控制中心 福州 350003；3.南平市延平区动物疫病预防控制中心 福建南平 353000）

近年来随着我国在国际上的地位不断提高，在当今世界拥有着举足轻重的地位， 作为世界第一大猪肉生产国和世界第一大猪肉消费国， 生猪肉的运输问题一直面临着巨大的挑战。 随着人们生活水平不断提高，人们越来越注重食品安全问题，特别是对于生鲜食品， 这就对生鲜食品冷链物流配送提出了更高的要求。 肉类属于鲜活农产品， 水分多容易被各种细菌、寄生虫等污染，具有易腐烂性等特点，如果处理不到位，会造成非常严重的食品安全问题[1]，直接和间接威胁及影响到人畜的健康安全。 因此，对生鲜肉类冷链运输的问题更应该找出最优化的方案。

1 背景及意义

目前国内农产品冷链物流的发展水平较为落后，生鲜物流还是以常温运输为主体的配送模式，生鲜食品的冷链流通率只有57%，而在欧美、日本等发达国家，易腐食品冷藏运输率已超过90%，冷链流通率更是高达95%～98%。 而且，冷链物流的成本比常温运输要高出6%左右， 我国冷链企业通常的利润率为10%，冷链利润率仅为8%左右，而发达国家冷链的利润率可以达到20%以上，冷链物流成本过高已成为制约冷链企业发展的重要因素。此外，冷链物流由于对温控的要求比较高， 冷链断链现象时有发生，产品腐烂变质更是屡见不鲜，我国冷链过程中的产品损耗率高达25%，从数据上很明显可以看出寻找最科学最优化的路线， 冲破眼前的局面迫在眉睫，特别是在基层县级的运输线路。

在实际调查过程中发现， 很多县级屠宰场生鲜肉品的配送路线未经精准计算，大多还采用无科学、无系统的运输方式， 无形中进一步加剧了冷链物流的成本损耗。为有效提升冷链物流的效率，本文以福州市永泰县为例对有关方面进行探讨， 永泰县常年平均气温在14.6～20.1 ℃，气温逐月变化基本近于周期性， 以1 月 （或2 月） 为最低， 月平均在5.5～11.0 ℃；7 月（或8 月）气温上升到最高值，月平均在23.0～29.0 ℃（见图1）[2]。 从屠宰场宰杀后配送给最远的洑口乡，最远距离为81.4 km，按冷藏车平均时速60 km/h 计算，单次配送也需要近90 min，目前该县屠宰场已经采用专用冷藏车冷链配送模式， 但要配送给各乡镇， 没有冷链将无法保证鲜肉在配送中达到质量需求。 为此，初步设定以一定约束条件[3]的假设基础上，以最短的总路程为目标函数，构建县级屠宰场生猪胴体冷链配送路线的最短路径优化算法。 并将该算法的结果作为指导并应用到实际生产中，为其他县域级冷链物流配送提供相应的参考。

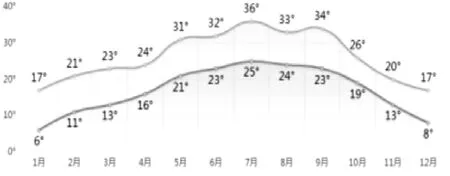
图1 永泰县历史各月气温趋势

2 问题描述与研究假设

以福州市永泰县青云食品公司屠宰场近年来生鲜肉品冷链配送的运输情况、车辆、线路、输送点、运输时间等为研究对象。 设定屠宰场配送中心共配备冷链运输车9 辆，其中2 辆载重2 000 kg，5 辆载重1 200 kg，2 辆载重350 kg。 为了能达到算法运算的构建要求，初步设定的约束条件假设为：（1）永泰县青云食品公司屠宰场仅有单一配送中心， 其所有冷链运输车均从该配送中心出发， 需要若干车辆完成对各乡镇生猪胴体配送点的鲜肉配送。（2）各乡镇生猪胴体配送点分布位置已知（见图2）。 （3）各乡镇生猪胴体配送点之间的距离已知。（4）各配送点与屠宰场配送中心之间的最短距离已知， 路途中排除堵车的情况。（5）各乡镇生猪胴体配送点的货物需求量和要求配送的时间窗已知， 排除路途中人为的耽搁时间。（6）配送路途中的内外温度保持恒定。（7）车辆型号、车速运行统一。 （8）每条配送线路上都只有一辆车进行配送， 且每个乡镇生猪胴体配送点冷链运输车只到达一次。 （9）配送过程中不存在装货的情况。

图2 永泰县屠宰场配送中心及各乡镇生猪胴体配送点分布情况

2.1 模型构建 路径优化算法采用遗传算法，2014 年王玥丹[4]证实遗传算法可应用于冷链配送路线的适用性。以最短的总路程为目标函数，从一个配送中心出发， 以同种型号车辆不同的数量所到达的不同需求点为已知条件， 构建县级屠宰场生鲜猪胴体冷链配送路线的最短路径优化算法。 主要考虑的参数为冷链运输车配送总时间和配送的最短路径。通过数学函数测算最短配送路径和时间， 确保冷藏生鲜猪胴体及时配送到各乡镇，满足群众的需求。

2.2 算法构建的参数及参数定义[5]k：表示车辆；m：表示车辆数目，车辆编号表示为k=1,2,......m；n：各乡镇生猪胴体配送点数目， 各乡镇配送点表示为i，j（i，j∈V，V={0,1,......n}）；V：表示任意不同的乡镇配送点（当V 等于0 时表示屠宰场配送中心）；tik，tjk：表示分别到达需求点i，j 的时间点；tei： 表示车辆到达需求点i 的最早时间点；tli：表示车辆到达需求点i的最晚时间点；pi： 表示需求点i 所需物料的备料时间；si：需求点i 所需物料的服务时间；dij：表示需求点i 和j 之间的距离；v： 配送车辆平均行驶速度；a：车辆每千米配送费用；Q： 配送车辆最大装载容量；Qi：第i 个需求点的需求量；Cα：车辆早于需求点最早满意时间点到达惩罚系数；Cβ： 车辆晚于需求点最晚满意时间点到达惩罚系数；X：表示屠宰车间待宰和生猪胴体装载时间（X={0,1,......n}）；y：表示各乡镇配送点卸载生猪胴体时间（y={0,1,......n}）；Z：表示各乡镇生猪胴体配送点卸载生猪胴体时间 （Z={0,1,......n}）。

2.3 模型构建步骤

2.3.1 冷链运输配送时间 为能在预定的时间内保证鲜肉在配送中达到质量需求， 在规定的路程上需要的最短冷链运输配送总时间就是冷链运输车的行驶时间、 屠宰车间待宰和生猪胴体装载时间以及各乡镇配送点卸载生猪胴体时间的算数和。

从需求点i 到需求点j 的行驶时间用公式表示为：tij=dij/v；冷链运输车的行驶时间表示为屠宰车间待宰和生猪胴体装载时间表示为：各乡镇生猪胴体配送点卸载生猪胴体时间表示为；冷链运输车配送总时间最少的函数表示为

2.3.2 冷链运输配送误差系数 在冷链运输过程及在设定的约束条件下总会出现概率性误差。 在整个模型的建立中， 按照存在不同的情况需要有相应的应对措施-惩罚系数。 本文中惩罚系数指的是冷藏生鲜猪胴体能否在各乡镇的配送点和需求点期望时间窗内到达。不同期望时间窗存在不同的惩罚系数。如果早于期望时间到达就通过早到惩罚系数进行惩罚， 如果晚于期望时间到达就设置晚到惩罚系数进行惩罚。

2.3.3 算法的约束条件 当m 辆冷链运输车均从同一个屠宰场的配送中心出发， 用公式表示为yok=m； 每个乡镇生猪胴体配送点均由一辆车配送，用公式表示为（i=1，2，...，n）；每个乡镇生猪胴体配送点有且只有一辆车访问一次， 用公式表示为（j=0，1，...，n）； 冷链运输车从屠宰场的配送中心出发，完成任务后返回配送中心，途中无装货，用公式表示为每条冷链配送路线上的所有乡镇生猪胴体配送点所需生猪胴体重量之和小于等于单位冷链运输车最大装载量，用公式表示为Q（k=1，2，...，m）；每个乡镇生猪胴体配送点到达的车辆和离开的车辆数目相同，用公式表示为同一配送路线上连续的两个乡镇生猪胴体配送点间， 冷链运输车到达前一乡镇生猪胴体配送点的时刻不超过到达后一乡镇生猪胴体配送点的时刻， 用公式表示为：xijk（tik+si+tij-tjk）≤0，（i≠j，k=1，2...，m）。

3 运算结果

应用Matlab2018a 编制与该算法匹配的程序，完成对屠宰场生鲜肉品配送算法的求解， 经过对算例进行多次随机试验，抽出的最优试验结果及图3-图4[6]。 在节假日期间预估生猪胴体高峰需求时，需使用冷链运输车8 辆， 其中使用载重350 kg 的2 辆，载重1 200 kg 的5 辆，载重2 000 kg 的1 辆，全部完成配送任务5 030.68 kg，冷链运输车总行驶距离为736.4 km，总行驶时间为12.29 h（见表2）。而在非节假日期间预估生猪胴体低峰需求时， 需使用冷链运输车7 辆， 其中使用载重350 kg 的2 辆，使用载重1 200 kg 的5 辆， 全部完成配送任务2 752.06 kg，冷链运输车总行驶距离为613.7 km，总行驶时间为10.22 h（见表3）。

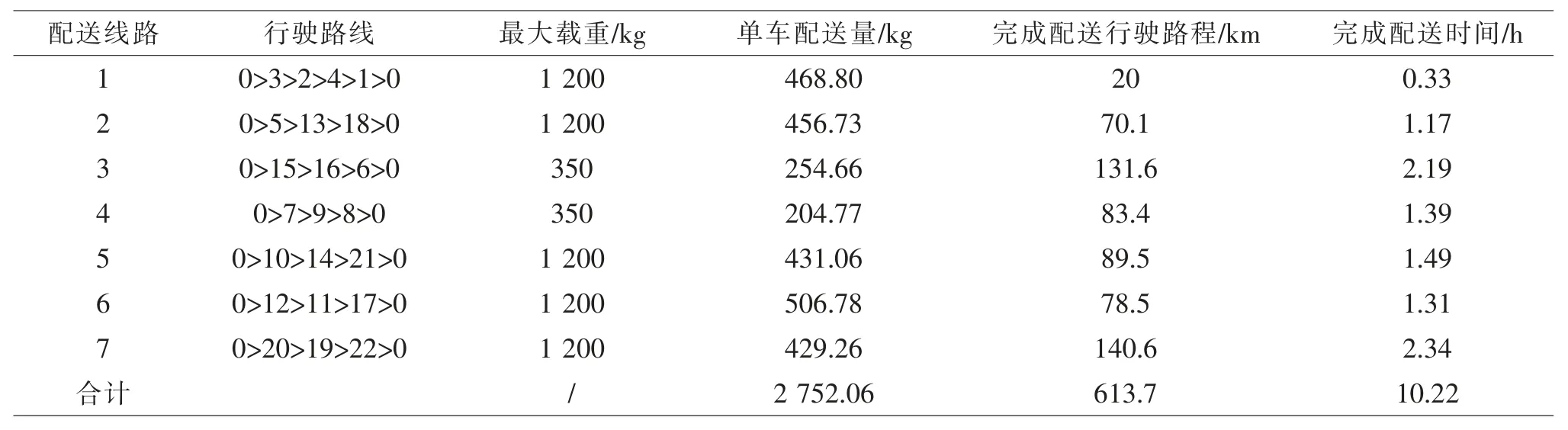
表3 非节假日期间冷链运输车行驶路线的配送情况模拟结果

图3 节假日期间车辆配送线路图

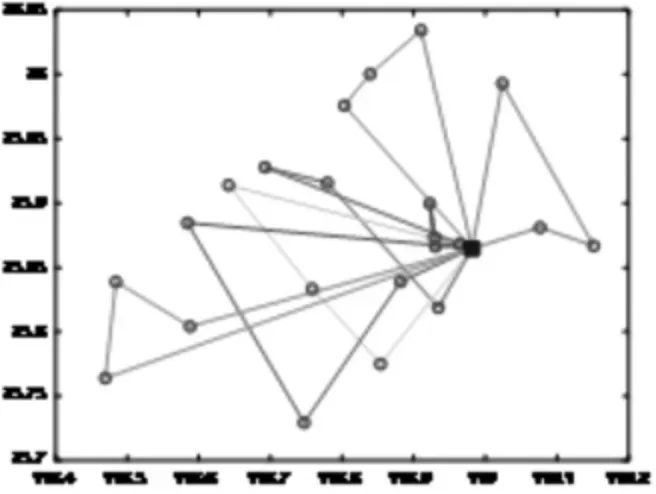
图4 非节假日期间车辆配送线路图

4 讨论分析

本算法采用遗传算法求解最短路径， 该遗传算法由美国密歇根大学John H H 教授及其学生在20世纪六七十年代提出，其具有自组织性、自适应性和自学习性的特性，是一种“生成+检测”的迭代搜索算法（见图5）[7]。 它以种群中的所有个体为操作对象、 每个个体对应问题的一个解。 选择、 交叉和变异是其3 个主要操作[8]。 遗传算法利用遗传算子进行组合交叉和变异， 逐代直到进化出代表最优解的种群。

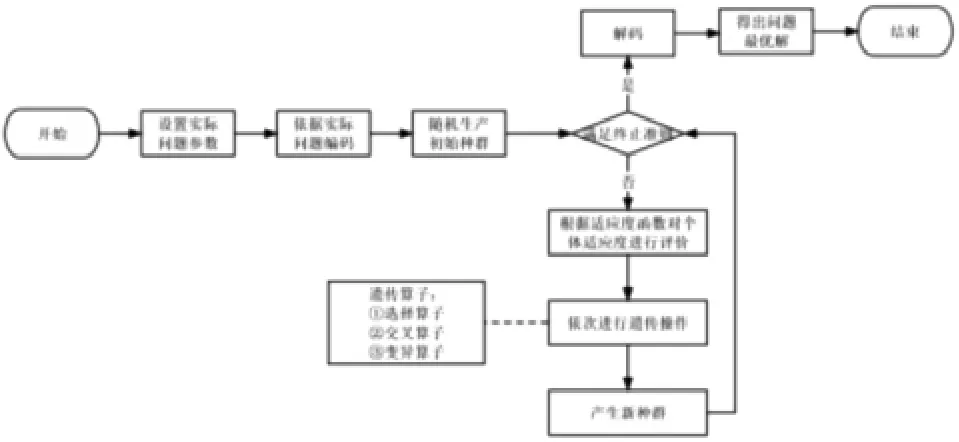
图5 遗传算法基本流程

本算法测算是通过数学算法估算较合理的车辆最短路径优化配置，在实际工作过程中，还需考虑车辆维修、维护、保养等车辆待场等情况，因此，该场配备一定的备用车辆就显得非常有必要。 从运行结果可以看出， 冷链运输车完成配送时间均控制在2 h左右，防止疲劳驾驶，保证驾驶人员的安全。 本算法测算目的是预估最短的行驶路线和最短的配送时间，但在目前低碳要求的情况下，还应该再考虑运输成本、热能损耗、实际路况、随机需求等问题，有待于下一步的算法测算中再进行优化。